Matlab函数——find
介绍
当你需要返回某个数组中符合指定条件的所有元素的索引时,可以使用 MATLAB 中的 `find` 函数。
`find` 函数语法:
indices = find(X)
indices = find(X, k)
indices = find(X, k, 'first')
indices = find(X, k, 'last')
其中,`X` 是一个数组,`indices` 是一个包含所有找到元素索引的列向量。如果 `X` 中有 `k` 个匹配元素,`indices` 将具有 `k` 个元素。`'first'` 或 `'last'` 可用于仅返回最先或最后匹配的元素索引。
例如:
A = [1 2; 3 4; 5 6];
ind = find(A >= 3)将返回:
ind =2356在这个例子中,`ind` 向量包含 `A` 数组中大于等于3的所有元素的索引值。 注意,这些索引是基于列的索引,因为 `A` 数组是列向量。
举例
当想要找到一个数组中大于某个特定值的元素的索引时,可以使用 `find` 函数。
例如,我们有一个数组 `A = [1, 4, 2, 5, 3]`,现在我们想找到所有大于等于3的元素的索引。
使用 `find` 函数可以这样实现:
A = [1, 4, 2, 5, 3];
indices = find(A >= 3);此时,`indices` 的值将为 `[2, 4, 5]`,表示在数组 `A` 中,位于索引 2、4 和 5 处的元素大于等于 3。
你还可以使用 `find` 函数的其他参数来指定返回的索引数量或仅返回第一个或最后一个匹配的索引。例如,如果只想返回前两个大于等于3的元素的索引,可以使用以下语法:
indices = find(A >= 3, 2);此时,`indices` 的值将为 `[2, 4]`,表示在数组 `A` 中,位于索引 2 和 4 处的前两个元素大于等于 3。
相关文章:

Matlab函数——find
介绍 当你需要返回某个数组中符合指定条件的所有元素的索引时,可以使用 MATLAB 中的 find 函数。 find 函数语法: indices find(X) indices find(X, k) indices find(X, k, first) indices find(X, k, last) 其中,X 是一个数组…...
mac安装python3
文章目录 1. 安装1.1 brew安装(失败)2. 下载安装包 2. 查看版本3. 配置 1. 安装 1.1 brew安装(失败) brew install python3下载完成后报错:Error: python3.10: unknown or unsupported macOS version: :dunno 解决&a…...
【星海出品】VUE(一)
Windows安装nvm控制器 Windows里找都PowerShell。右击点击管理员运行。 1.安装choco Set-ExecutionPolicy Bypass -Scope Process -Force; iex ((New-Object System.Net.WebClient).DownloadString(https://chocolatey.org/install.ps1))2.安装NVM choco install nvm 3.查看可…...

Stable Diffusion 的提示词使用技巧
推荐Stable Diffusion自动纹理工具: DreamTexture.js自动纹理化开发包 什么是提示语? 提示语是人工智能中的一个重要组成部分,尤其是自然语言处理 (NLP)。在AI自人工智能中,想要获得好的效果,简…...

Hook函数
在嵌入式系统中,hook函数(也被称为钩子函数)是一种特殊类型的函数,它会在特定的事件发生时被操作系统内部调用。例如,在实时操作系统(RTOS)中,如果删除了一个任务,就会调…...

USB简介系列-01
文章目录 USB简介一、电气USB简介 通用串行总线(USB)是由Compaq,Intel,Microsoft和NEC开发的规范,后来惠普,朗讯和飞利浦加入。这些公司成立了 USB Implementers Forum, Inc 作为一家非营利性公司,以发布规范并组织 USB 的进一步开发。 USB-IF的目的是为当时使用的PC…...

算法小白的心得笔记:比较小数点后五位,而不会受到浮点数精度问题的影响。
epsilon 来比较浮点数 double epsilon 1e-6; // for 6 decimal places for (const auto &ratio : colorRatio) {std::cout << "__" << inum << "__" << ratio << " ";if ((inum - 1) % 10 0){std::cout &l…...
11月起,33个省份纳入数电票开票试点范围内,发票无纸化已是大势所趋!
10月底,北京、贵州、山东(不含青岛市)、湖南、宁夏5个地区相继发布开展数电票试点工作的通知,至此,全国已有33个省份纳入数电票开票试点范围内。根据上述5地区发布的相关公告,11月1日将正式推行“数电票”开…...
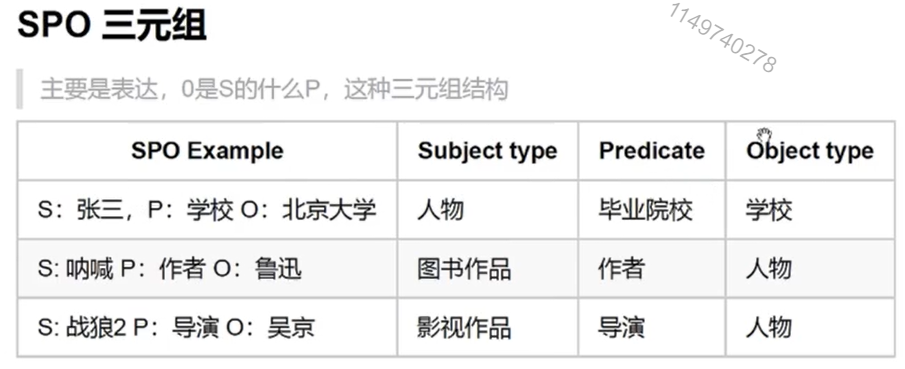
NLP之Bert多分类实现案例(数据获取与处理)
文章目录 1. 代码解读1.1 代码展示1.2 流程介绍1.3 debug的方式逐行介绍 3. 知识点 1. 代码解读 1.1 代码展示 import json import numpy as np from tqdm import tqdmbert_model "bert-base-chinese"from transformers import AutoTokenizertokenizer AutoToken…...
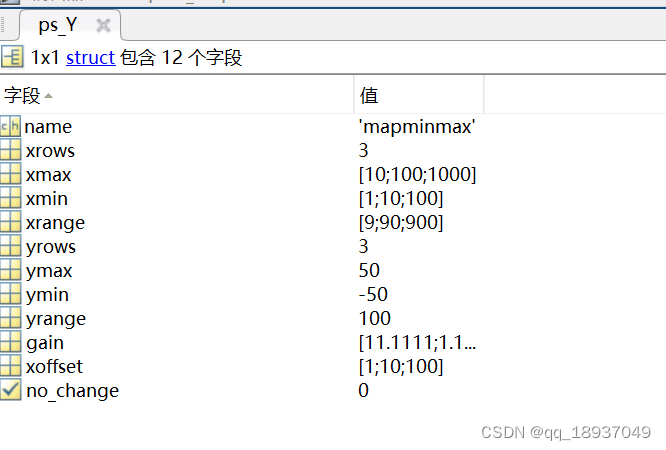
matlab中的mapminmax函数初步理解和应用
matlab中的mapminmax函数初步认识 一、mapminmax 顾名思义:映射最大最小 二、语法及举例 2.1 语法1 [Y,PS] mapminmax(X) 将矩阵X映射形成矩阵Y, Y中每行中的最小值对应-1,最大值对应1。PS是一个包含映射信息的结构体。 举例: clc cle…...

svc和ingress的关系
在Kubernetes中,SVC有三种类型,分别是ClusterIP、NodePort和LoadBalancer。而Ingress则是一种服务类型的扩展,它主要用于处理HTTP和HTTPS流量,并提供了对集群内部服务的路由和负载均衡功能。 下面简要介绍SVC的三种类型和Ingress…...

可以使用以下代码对数据库查询结果进行分组统计
public static void GroupAndStatistic(string connectionString, string query) {// 创建一个SQLSugar实例var db new SQLSugarClient(connectionString);// 使用QueryHelper类执行查询var dataTable db.Query<DataRow>().From(query).ExecuteDataTable();// 使用LINQ…...
win10提示mfc100u.dll丢失的解决方法,快速解决dll问题
在计算机使用过程中,我们经常会遇到一些错误提示,其中之一就是“mfc100u.dll丢失”。那么,mfc100u.dll是什么?mfc100u.dll是Microsoft Visual C Redistributable文件之一,它包含了用于MFC (Microsoft Foundation Class…...
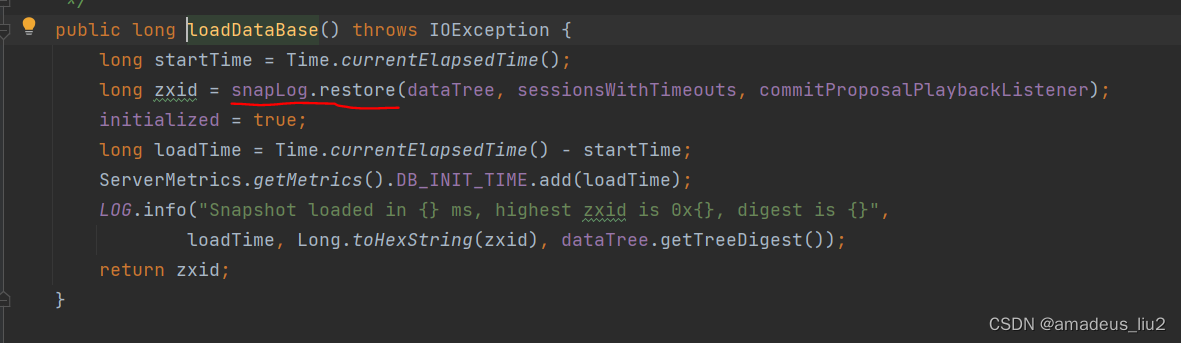
zookeeper:启动原理
主类: QuorumPeerMain, 其中调用了main对象的initializeAndRun方法, 首先定义了QuorumPeerConfig对象,然后调用了parse方法,parse方法代码如下: 其中调用的parseProperties方法的代码如下: 可以看到&am…...

kafka问题汇总
报错1: 解决方式 1、停止docker服务 输入如下命令停止docker服务 systemctl stop docker 或者service docker stop1 停止成功的话,再输入docker ps 就会提示出下边的话: Cannot connect to the Docker daemon. Is the docker daem…...
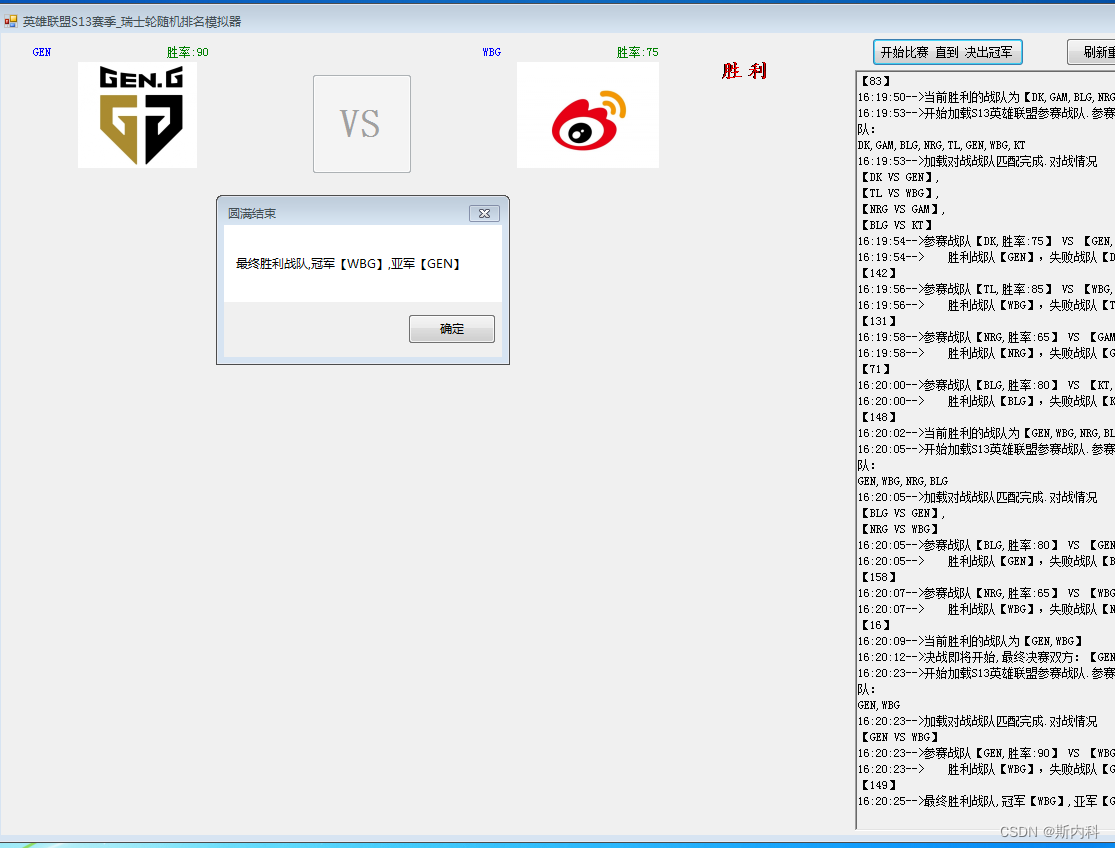
C#使用随机数模拟英雄联盟S13瑞士轮比赛
瑞士轮赛制的由来 瑞士制:又称积分循环制,最早出现于1895年在瑞士苏黎世举办的国际象棋比赛中,故而得名。其基本原则是避免种子选手一开始就交锋、拼掉,是比较科学合理、用得最多的一种赛制;英语名称为Swiss System。…...
利用限流实现不公平分发)
RabbitMQ(高级特性)利用限流实现不公平分发
在RabbitMQ中,多个消费者监听同一条队列,则队列默认采用的轮询分发。但是在某种场景下这种策略并不是很好,例如消费者1处理任务的速度非常快,而其他消费者处理速度却很慢。此时如果采用公平分发,则消费者1有很大一部分…...

3 网络协议入门
从淘宝买东西举例来说明一次请求中的,网络有关的部分是打开浏览器,输入购物网站的地址: https://www.taobao.com/那么浏览器是怎么打开购物网站的首页的呢? (1)首先受到了一段http报文 HTTP/1.1 200 OK Date: Tue, 27 Mar 2018 …...
)
【星海出品】VUE(五)
表单 表单输入绑定 只需要v-model声明一下这个变量就可以。 还可以选择不同的类型,例如 type"checkbox“ v-model 也提供了 lazy、number、.trim 功能,只需要在v-model后面加入.lazy 例如:v-model.lazy”message“ <template><…...
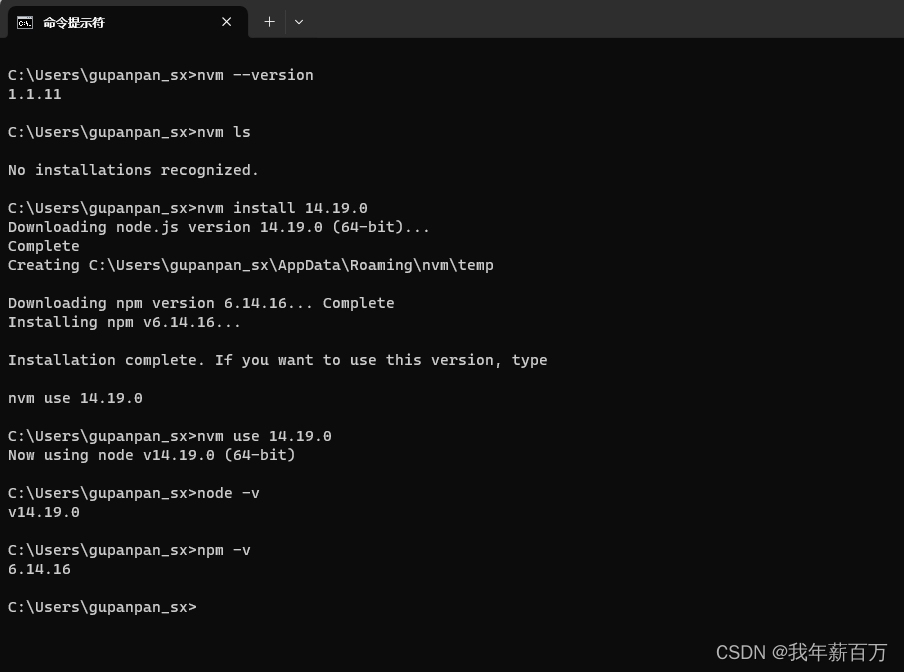
项目实战之安装依赖npm install
文章目录 nvmdeasync包和node-gyp报错deasync包node-gyp报错 前言:有些人看着还活着其实已经凉了好一会儿了。 初拿到项目 初拿到项目肯定是先看配置 package.json的啦,看看都需要安装什么依赖,然后 npm install,OK结束 皆大欢喜。 ————…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...
