算法小白的心得笔记:比较小数点后五位,而不会受到浮点数精度问题的影响。
epsilon 来比较浮点数
double epsilon = 1e-6; // for 6 decimal places
for (const auto &ratio : colorRatio)
{std::cout << "__" << inum << "__" << ratio << " ";if ((inum - 1) % 10 == 0){std::cout << std::endl;}if (!std::isnan(ratio) && !std::isnan(beta3[inum - 1])){if (std::abs(ratio - beta3[inum - 1]) > epsilon){std::cerr << "\n __" << inum << "__ 计算错误 " << ratio << " 应该是 " << beta3[inum - 1] << std::endl;return 1;}}inum++;
}
double epsilon = 1e-6; // for 6 decimal places
我们可以设置 epsilon 的值来指定有效精度位,如 1e-5是五位精度。
可以比较负数的版本
在上述代码中,我们使用的是std::abs函数来计算两个浮点数之间的差的绝对值,这个函数同样适用于负数。因此,无论你的浮点数是正数还是负数,这段代码都能正确地比较它们的差是否小于epsilon。
如果你的ratio和beta3[inum - 1]都可能是负数,并且你想要比较它们的绝对值,你可以在比较之前先使用std::abs函数将它们转换为正数,如下所示:
if (std::abs(std::abs(ratio) - std::abs(beta3[inum - 1])) > epsilon)
{std::cerr << "\n __" << inum << "__ 计算错误 " << ratio << " 应该是 " << beta3[inum - 1] << std::endl;return 1;
}
这段代码会先计算ratio和beta3[inum - 1]的绝对值,然后再比较它们的差是否小于epsilon。这样,无论你的浮点数是正数还是负数,这段代码都能正确地比较它们。
可能出现的一些问题
由于浮点数在计算机中的表示和存储方式导致的相等内容被判定为不相等。
这个问题可能是由于浮点数在计算机中的表示和存储方式导致的。浮点数在计算机中的表示并不是完全精确的,因此即使两个浮点数在理论上应该相等,但由于精度问题,它们可能在计算机中不相等。
在上述的代码中,使用了一个非常小的正数(称为“epsilon”),如果两个浮点数的差的绝对值小于这个epsilon,那么我们就可以认为这两个浮点数是相等的。这是一种常见的处理浮点数精度问题的方法。
然而,如果epsilon 设置得太小了,导致了这个问题。 可以尝试增大epsilon的值,例如将其设置为1e-5或1e-4,看看是否能解决这个问题。
另外, 也可以尝试使用其他的比较浮点数的方法,例如使用std::nextafter函数。这个函数可以返回在给定方向上,距离给定浮点数最近的下一个可表示的浮点数。你可以使用这个函数来比较两个浮点数是否相等,如下所示:
if (ratio != std::nextafter(beta3[inum - 1], std::numeric_limits<double>::lowest()) &&ratio != std::nextafter(beta3[inum - 1], std::numeric_limits<double>::max()))
{std::cerr << "\n __" << inum << "__ 计算错误 " << ratio << " 应该是 " << beta3[inum - 1] << std::endl;return 1;
}
这段代码会比较ratio是否等于beta3[inum - 1]的下一个或上一个可表示的浮点数。如果不等于,那么我们就认为这两个浮点数不相等。这种方法可以更精确地比较浮点数,而不会受到精度问题的影响。
分享一个有趣的 学习链接:https://xxetb.xet.tech/s/HY8za
相关文章:

算法小白的心得笔记:比较小数点后五位,而不会受到浮点数精度问题的影响。
epsilon 来比较浮点数 double epsilon 1e-6; // for 6 decimal places for (const auto &ratio : colorRatio) {std::cout << "__" << inum << "__" << ratio << " ";if ((inum - 1) % 10 0){std::cout &l…...
11月起,33个省份纳入数电票开票试点范围内,发票无纸化已是大势所趋!
10月底,北京、贵州、山东(不含青岛市)、湖南、宁夏5个地区相继发布开展数电票试点工作的通知,至此,全国已有33个省份纳入数电票开票试点范围内。根据上述5地区发布的相关公告,11月1日将正式推行“数电票”开…...
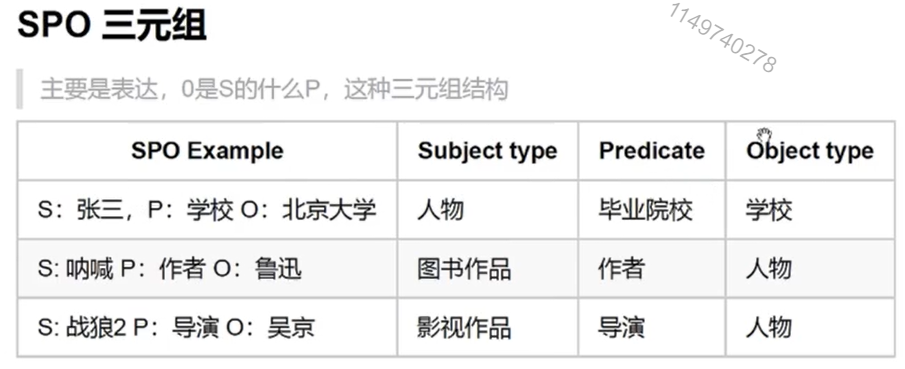
NLP之Bert多分类实现案例(数据获取与处理)
文章目录 1. 代码解读1.1 代码展示1.2 流程介绍1.3 debug的方式逐行介绍 3. 知识点 1. 代码解读 1.1 代码展示 import json import numpy as np from tqdm import tqdmbert_model "bert-base-chinese"from transformers import AutoTokenizertokenizer AutoToken…...
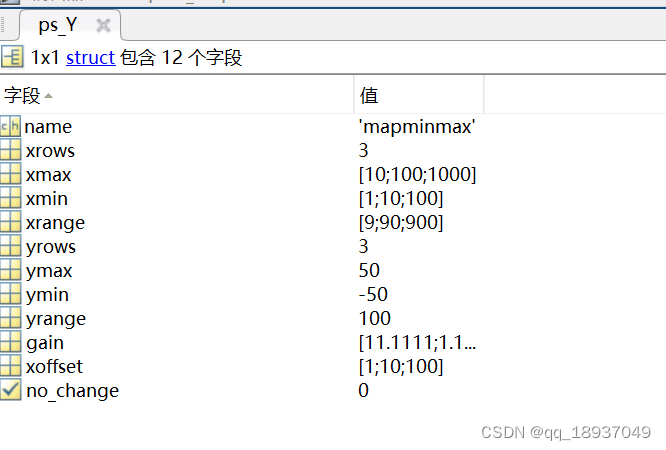
matlab中的mapminmax函数初步理解和应用
matlab中的mapminmax函数初步认识 一、mapminmax 顾名思义:映射最大最小 二、语法及举例 2.1 语法1 [Y,PS] mapminmax(X) 将矩阵X映射形成矩阵Y, Y中每行中的最小值对应-1,最大值对应1。PS是一个包含映射信息的结构体。 举例: clc cle…...

svc和ingress的关系
在Kubernetes中,SVC有三种类型,分别是ClusterIP、NodePort和LoadBalancer。而Ingress则是一种服务类型的扩展,它主要用于处理HTTP和HTTPS流量,并提供了对集群内部服务的路由和负载均衡功能。 下面简要介绍SVC的三种类型和Ingress…...

可以使用以下代码对数据库查询结果进行分组统计
public static void GroupAndStatistic(string connectionString, string query) {// 创建一个SQLSugar实例var db new SQLSugarClient(connectionString);// 使用QueryHelper类执行查询var dataTable db.Query<DataRow>().From(query).ExecuteDataTable();// 使用LINQ…...
win10提示mfc100u.dll丢失的解决方法,快速解决dll问题
在计算机使用过程中,我们经常会遇到一些错误提示,其中之一就是“mfc100u.dll丢失”。那么,mfc100u.dll是什么?mfc100u.dll是Microsoft Visual C Redistributable文件之一,它包含了用于MFC (Microsoft Foundation Class…...
zookeeper:启动原理
主类: QuorumPeerMain, 其中调用了main对象的initializeAndRun方法, 首先定义了QuorumPeerConfig对象,然后调用了parse方法,parse方法代码如下: 其中调用的parseProperties方法的代码如下: 可以看到&am…...

kafka问题汇总
报错1: 解决方式 1、停止docker服务 输入如下命令停止docker服务 systemctl stop docker 或者service docker stop1 停止成功的话,再输入docker ps 就会提示出下边的话: Cannot connect to the Docker daemon. Is the docker daem…...
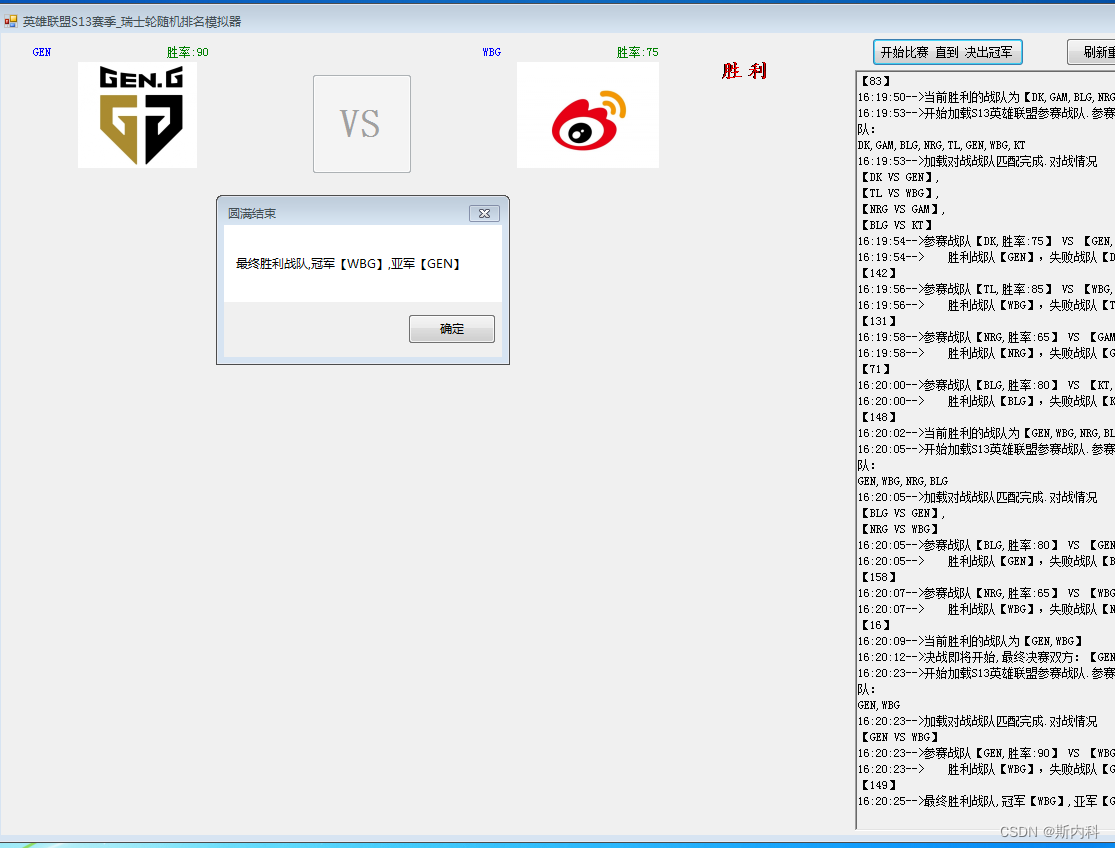
C#使用随机数模拟英雄联盟S13瑞士轮比赛
瑞士轮赛制的由来 瑞士制:又称积分循环制,最早出现于1895年在瑞士苏黎世举办的国际象棋比赛中,故而得名。其基本原则是避免种子选手一开始就交锋、拼掉,是比较科学合理、用得最多的一种赛制;英语名称为Swiss System。…...
利用限流实现不公平分发)
RabbitMQ(高级特性)利用限流实现不公平分发
在RabbitMQ中,多个消费者监听同一条队列,则队列默认采用的轮询分发。但是在某种场景下这种策略并不是很好,例如消费者1处理任务的速度非常快,而其他消费者处理速度却很慢。此时如果采用公平分发,则消费者1有很大一部分…...

3 网络协议入门
从淘宝买东西举例来说明一次请求中的,网络有关的部分是打开浏览器,输入购物网站的地址: https://www.taobao.com/那么浏览器是怎么打开购物网站的首页的呢? (1)首先受到了一段http报文 HTTP/1.1 200 OK Date: Tue, 27 Mar 2018 …...
)
【星海出品】VUE(五)
表单 表单输入绑定 只需要v-model声明一下这个变量就可以。 还可以选择不同的类型,例如 type"checkbox“ v-model 也提供了 lazy、number、.trim 功能,只需要在v-model后面加入.lazy 例如:v-model.lazy”message“ <template><…...
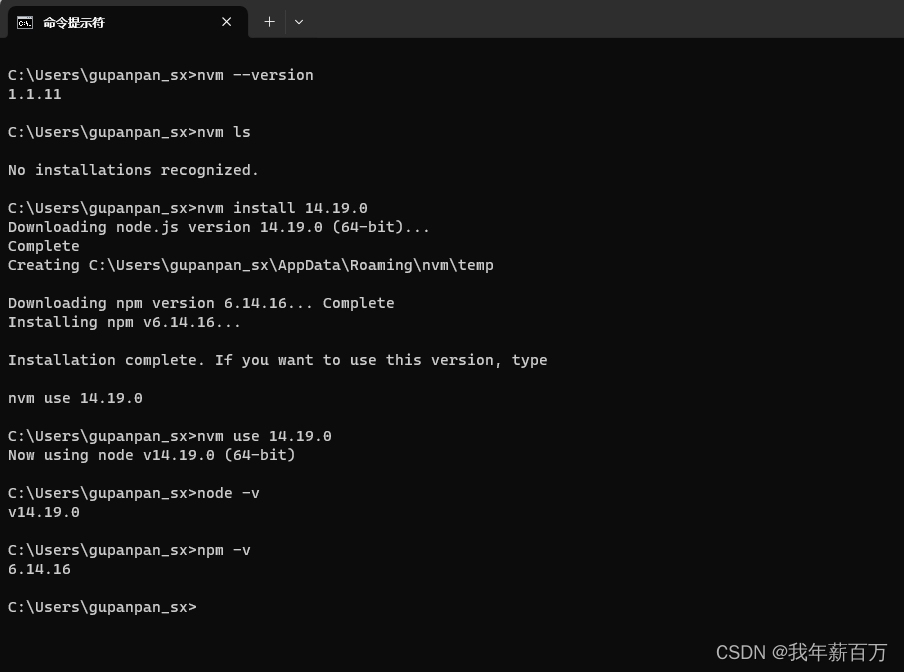
项目实战之安装依赖npm install
文章目录 nvmdeasync包和node-gyp报错deasync包node-gyp报错 前言:有些人看着还活着其实已经凉了好一会儿了。 初拿到项目 初拿到项目肯定是先看配置 package.json的啦,看看都需要安装什么依赖,然后 npm install,OK结束 皆大欢喜。 ————…...

Java之图书管理系统
🤷♀️🤷♀️🤷♀️ 今天给大家分享一下Java实现一个简易的图书管理系统! 清风的个人主页🎉✏️✏️ 🌂c/java领域新星创作者 🎉欢迎👍点赞✍评论❤️收藏 😛&…...

用「埋点」记录自己,不妄过一生
最近有朋友问我「埋点怎么做」,给朋友讲了一些互联网广告的案例,从源头的数据采集讲到末尾的应用分析和流量分配等(此处省略N多字) 解释完以后,我想到一个问题:有了埋点可以做分析,那我们对自己…...

运维知识点-Docker从小白到入土
Docker从小白到入土 安装问题-有podmanCentos8使用yum install docker -y时,默认安装的是podman-docker软件 安装docker启动dockeryum list installed | grep dockeryum -y remove xxxx安装Docker安装配置下载安装docker启动docker,并设置开机启动下载所…...
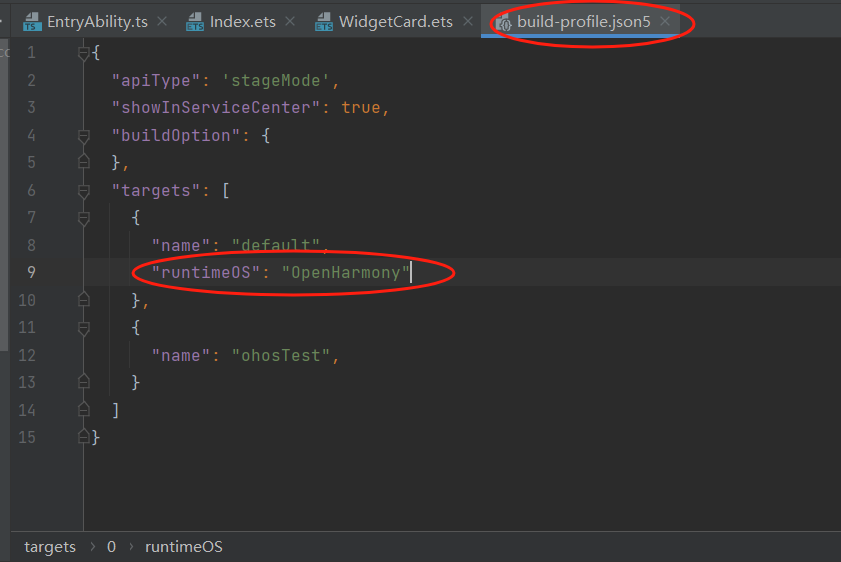
基于DevEco Studio的OpenHarmony应用原子化服务(元服务)入门教程
一、创建项目 二、创建卡片 三、应用服务代码 Index.ets Entry Component struct Index {State TITLE: string OpenHarmony;State CONTEXT: string 创新召见未来!;build() {Row() {Column() {Text(this.TITLE).fontSize(30).fontColor(0xFEFEFE).fontWeight(…...
,一个SQL语句是如何执行的呢?)
MySQL和Java程序建立连接的底层原理(JDBC),一个SQL语句是如何执行的呢?
Java程序方面 1. JDBC驱动程序:JDBC驱动程序是连接MySQL数据库的核心组件。它是一组Java类,用于实现与MySQL数据库的通信协议和数据传输。驱动程序负责将Java程序发送的请求转化为MySQL数据库能够理解的格式,并将数据库返回的结果转化为Java…...
uniapp踩坑之项目:uniapp数字键盘组件—APP端
//在components文件夹创建digitKeyboard文件夹,再创建digitKeyboard.vue <!-- 数字键盘 --> <template><view class"digit-keyboard"><view class"digit-keyboard_bg" tap"hide"></view><view clas…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
