动态规划-丑数
**
描述
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第 n个丑数。
数据范围:
0≤n≤2000
要求:空间复杂度 O(n) , 时间复杂度 O(n)
示例1
输入:7
返回值:8
题目分析
我们先看到题目,把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。
有了上面的定义我们就可以知道,丑数的形式就是2x3y5z.所有的丑数都会是由2x3y5^z组成的.
因此我们只需要根据此公式从小到大列举出每一个丑数,那么我们就能找到第n个丑数.
由于,x,y,z都是幂次方,且如果要从小到大寻找丑数,那么x,y,z都会逐渐增加,若想找到后一个幂次方的丑数,那么我们肯定会需要找到前一个幂次方的丑数.这时候我们就会想到用动态规划来解决此问题,因为我们可以将第n个丑数一直分解到第一个丑数,根据动态规划的转移方程,我们就可以一步步找到第n个丑数.
题解
说到动态规划,我们肯定会想到动态规划的三个步骤
1.确定状态
2.定义状态转移方程
3.求得最优解
1.确定状态
首先我们应该确定动态规划的起始状态,根据题干,我们能发现第一个丑数就是,我们即dp[0]=1,且此时x,y,z的值肯定都是0,即x=0,y=0,z=0.
2.定义状态转移方程
状态转移方程是这个题目的难点,我们需要知道如何通过状态转移方程来实现下一个丑数的定位,我们通过分析函数dp[i]=2x3y5z(其中i是第i个丑数的下标存储位置)可知,我们只要分别增大幂x,y,z,(x,y,z都从0开始增大)然后进行比较,我们就能找到我们想要的下一个丑数。
比如dp[0]=1,那么dp[1]的值,就是需要比较
213050 ,203150 ,203051 这三个值的大小,得出dp[1]=213050 = 2
因为213050 已经给dp[1],因此需要将第一个位置增大继续进行比较,那么如何进行增大呢?
这个地方也是本题最难理解的地方。我们先回到本题dp[i]=2x3y5z 这个函数上,我们可以想一下dp[i+1]有什么规律,dp[i+1]无非就是dp[i-k]*2,dp[i-k]*3,dp[i-k]*5 (k<i),三个其中的一个值,其中K可以是任意一个值,不一定是1.我们也可以反过来想,dp[i+1]/2,dp[i+1]/3,dp[i+1]/5的其中一个值,一定是dp[i]。所以我们这里只需要列出三路函数,第一路是关于dp[x]*2的函数,第二路是关于dp[y]*3,第三路是关于dp[z]*5的函数然后一直比较,就可以逐一找到每个丑数。其中x,y,z都是每一路线性增长的下标。这里需要解释一下为什么要分三路,因为d[i]的每次结果都需要乘2,乘3和乘5,以达到所有的质数都会被比较到的目的。且dp[i]乘2,乘3,乘5的值比较的时机是不同的。所以必须分为3个下标来分别统计幂x,y,z增长的值,从而进行动态规划比较。
求dp[2]:
根据上面的规则,第一个位置增大的值是dp[x=1]*2=(213050)*2=4
所以dp[2]的值,需要比较
223050 ,203150 ,203051 这三个值的大小,得出dp[2]=203150 = 3
求dp[3]:
同理第二个位置被取出,增大第二个位置,即dp[y=1]*3=(213050)*3=6
所以dp[3]的值,需要比较
223050 ,21315^0 ,203051 这三个值的大小,得出dp[3]=223050 = 4
求dp[4]:
后面为了便于观看,将直接用数字来代替,
接着第一个位置被取出,所以x需要继续增加,即dp[x=2]*2=3*2=6
dp[4]的值,需要比较
6 ,6 ,5 这三个值的大小,得出dp[4]=5
求dp[5]:
第三个数增大为dp[z=1]*5=2*5=10
dp[5]的值,需要比较
6 ,6 ,10 这三个值的大小,得出dp[5]=6,这时,一二位置都为6,所以都要增大,
即第一个位置dp[x=3]*2=4*2=8,第二个位置dp[y=2]*3=9
所以dp[5]的值需要比较
8,9,10这个三个数,得出dp[5]=8.
3.求得最优解
以此类推,就能列举出所有的丑数了。
下面是一个更为直观的动画图来解释此过程:

接下来就是算法部分:
public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可* ** @param index int整型* @return int整型*/public int GetUglyNumber_Solution (int index) {if(index<=6){return index;}int[] dp = new int[index];dp[0] = 1;int x=0,y=0,z=0;for(int i=1;i<dp.length;i++){dp[i] = Math.min(dp[z]*5,Math.min(dp[x]*2,dp[y]*3));if(dp[i] == dp[x]*2){x++;}if(dp[i] == dp[y]*3){y++;}if(dp[i] == dp[z]*5){z++;}}return dp[index-1];}
}
相关文章:

动态规划-丑数
** 描述 把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第 n个丑数。 数据范围: 0≤n≤2000 要求&#x…...
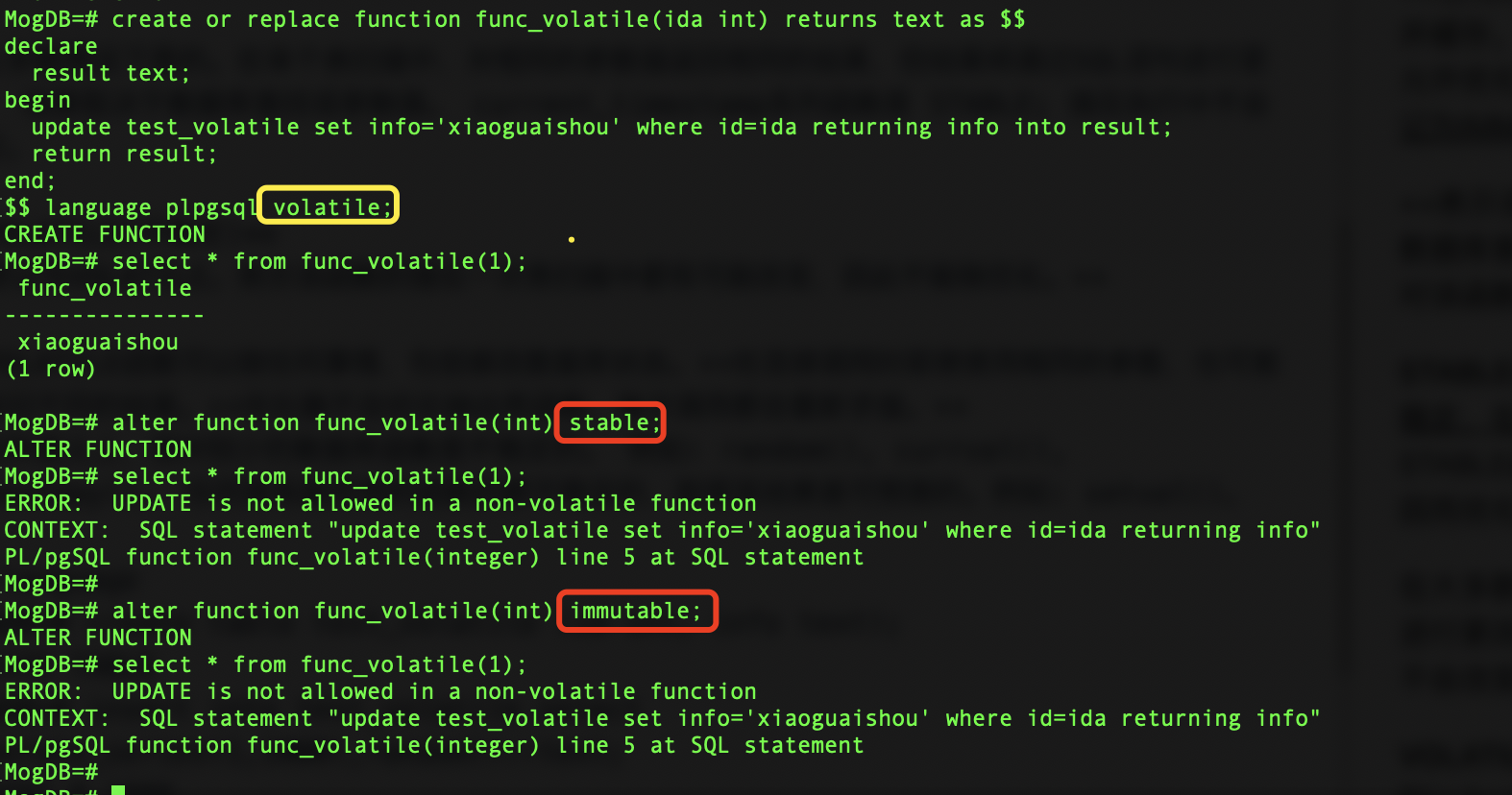
【MogDB/openGauss的三种函数稳定性关键字】
一、ORACLE中的类似的函数稳定性关键字(DETERMINISTIC) 在ORACLE里,function有着一个DETERMINISTIC参数,它表示一个函数在输入不变的情况下输出是否确定,只要输入的参数一样,返回的结果一定一样的…...

java-对Integer.MAX_VALUE做加法
public static void main(String[] args) {int maxValue Integer.MAX_VALUE;System.out.println("maxValue1 " (maxValue1));System.out.println("maxValue2 " (maxValue2));System.out.println("maxValue3 " (maxValue3));}//结果 maxVa…...

【学习笔记】[COCI2018-2019#1] Teoretičar
首先,可以发现 C C C等于所有点度数的最大值,我们能用到的颜色数目为 2 x ≥ C 2^x\ge C 2x≥C。 考虑分治,将边集划分为 E E 1 E 2 EE_1E_2 EE1E2,使得 E 1 , E 2 E_1,E_2 E1,E2中点度数的最大值都不超过 2 x − 1 2^…...

64位Office API声明语句第112讲
跟我学VBA,我这里专注VBA, 授人以渔。我98年开始,从源码接触VBA已经20余年了,随着年龄的增长,越来越觉得有必要把这项技能传递给需要这项技术的职场人员。希望职场和数据打交道的朋友,都来学习VBA,利用VBA,起码可以提高…...

C++ day3作业
1> 思维导图 2> 自己封装一个矩形类(Rect),拥有私有属性:宽度(width)、高度(height), 定义公有成员函数: 初始化函数:void init(int w, int h) 更改宽度的函数:set_w(int w) 更改高度的函数:set_h(int h) 输出该矩形的周长和面积函数:void s…...

蓝桥杯官网填空题(方格计数)
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 如下图所示,在二维平面上有无数个 11 的小方格。 我们以某个小方格的一个顶点为圆心画一个半径为 50000 的圆。 你能计算出这个圆里有多少个完整的小方…...

【系统架构设计】计算机公共基础知识: 6 知识产权与标准化
一 知识产权 1 保护对象和范围 法律法规名称保护对象及范围注意事项著作权法著作权 文学、绘画、摄影等作品 不需要申请,作品完成就开始保护。 绘画或摄影作品原件出售(赠予)著作权归还原作者,原件拥有者有所有权和展览权。 软件著作权法 计算机软件保护条例 软件著作权 软…...

【新】致远OA从前台XXE到RCE漏洞分析
0x01 前言 致远OA是目前国内最流行的OA系统之一,前几年也曾爆出过多个安全漏洞。致远官方一直对修复漏洞的态度十分积极,目前能有效利用的致远漏洞已经很少了。 和我们之前分享过的通达OA的漏洞类似,这类主流OA系统现在想要直接一步达到RCE的…...
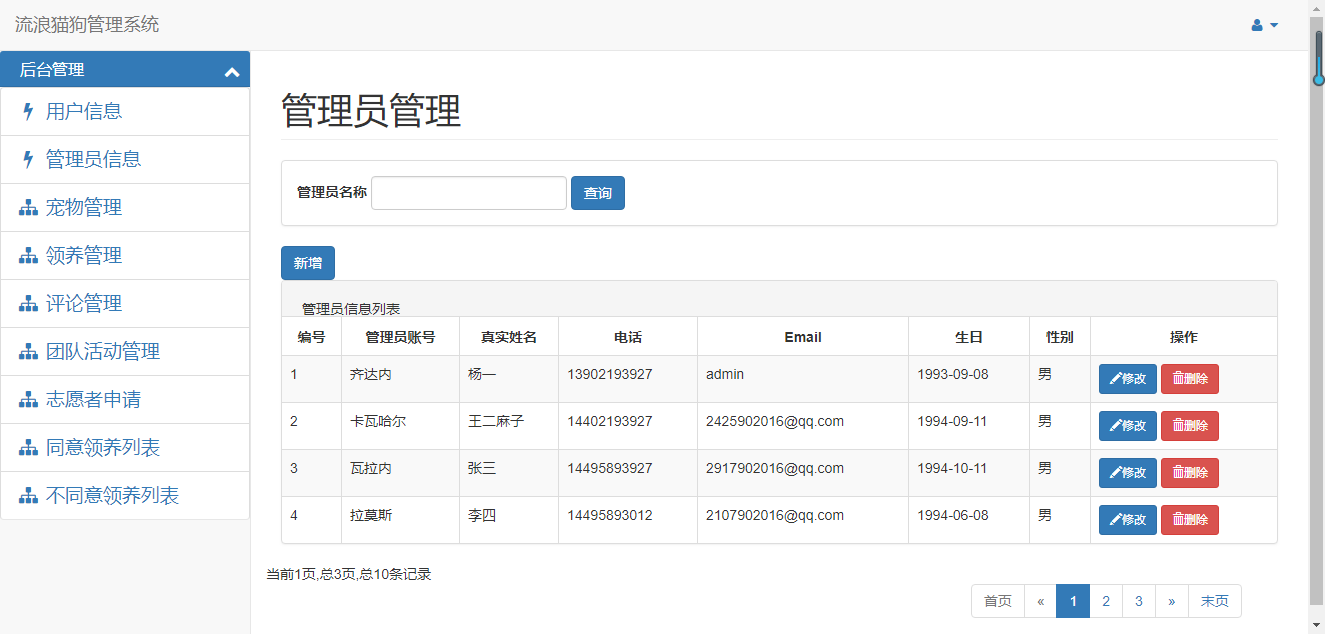
宠物领养系统jsp+servlet+mysql
设计不同用户的操作权限、注册和登录方法。 管理员可以在管理员管理、用户管理、宠物管理、评论管理、团队活动管理、志愿者的申请等等模块中进行查询、添加、删除、修改。 管理员可以在领养管理中通过领养时间查询所有宠物被领养的信息,修改是否同意领养宠物&#…...

MySQL 数据库安全性练习题
数据库安全性 一、实验目的 (1)熟悉通过MySQL对数据进行安全性控制 二、实验环境 Windows 11 MySQL Navicat 三、实验内容 今有以下两个关系模式: 职工(职工号,姓名,年龄,职务,工…...

如何使用Node.js快速创建HTTP服务器并实现公网访问本地Server
文章目录 前言1.安装Node.js环境2.创建node.js服务3. 访问node.js 服务4.内网穿透4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5.固定公网地址 前言 Node.js 是能够在服务器端运行 JavaScript 的开放源代码、跨平台运行环境。Node.js 由 OpenJS Foundation࿰…...
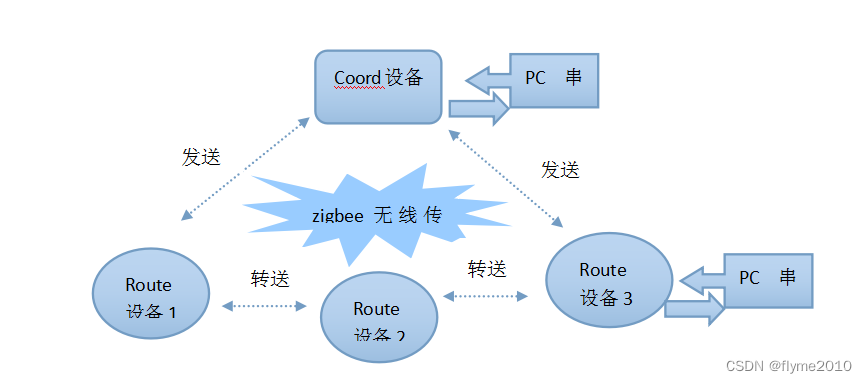
zigbee路灯无线通讯机制
zigbee路灯无线通讯机制 wang20160630 前言 目前路灯上通讯主要有电力载波和无线通讯;各有利弊,众说纷纭;本文不对两种技术进行比较,也不讨论哪种好,毕竟同种通讯模块,有的开发出来稳定,有的…...

asp.net docker-compose添加kafka和redis和zookeeper
docker-compose.yml添加 redis:image: redis:alpinekafka:image: "bitnami/kafka:3.1.1"depends_on:- zookeeperzookeeper:image: "bitnami/zookeeper:3.5.10" docker-compose.override.yml添加 redis:ports:- "6379"kafka:links: - zookeepere…...

2024上海国际人工智能展(CSITF)“创新驱动发展·科技引领未来”
人工智能(Artificial Intelligence,AI)作为当今世界科技发展的关键领域之一,正不断推动着各行各业的创新和变革。作为世界上最大的消费市场之一,中国正在积极努力将AI技术与产业融合并加速推广应用。在这个背景下&…...

汽车标定技术(三)--XCP协议如何支持测量功能
目录 1. 概述 2. 测量方式 -- Poll 3. 测量方式 -- DAQ 3.1 ODT概念模型 3.2 DAQ List概念 3.3 ODT 绝对编号和相对编号 3.4 静态DAQ和动态DAQ模式 (1)静态DAQ (2)动态DAQ 4.小结 1. 概述 在该系列的首篇文章汽车标定技…...

[c++]你最喜爱的stringstream和snprintf性能深入剖析
最近写一个程序中两个差不多的模块,一个使用了snprintf输出中间数据,另一个偷懒使用stringstream。结果你猜怎么着?居然压帧了!!到底是谁拖了性能的后退? 来自阿里云的性能分析实验 我上网一搜࿰…...
windows 用vs创建cmake工程并编译opencv应用项目生成exe流程简述
目录 前言一、安装opencv(1)下载(2)双击安装(3)环境变量和system文件夹设置 二、打开vs创建项目三、编辑cpp,.h,cmakelist.txt文件(1)h文件(2&…...
QML 仪表盘小示例
本次项目已发布在CSDN->GitCode,下载方便,安全,可在我主页进行下载即可,后面的项目和素材都会发布这个平台。 个人主页:https://gitcode.com/user/m0_45463480怎么下载:在项目中点击克隆,windows:zip linux:tar.gz tar # .pro TEMPLATE = appTARGET = dialcontrol#…...
力扣206. 反转链表
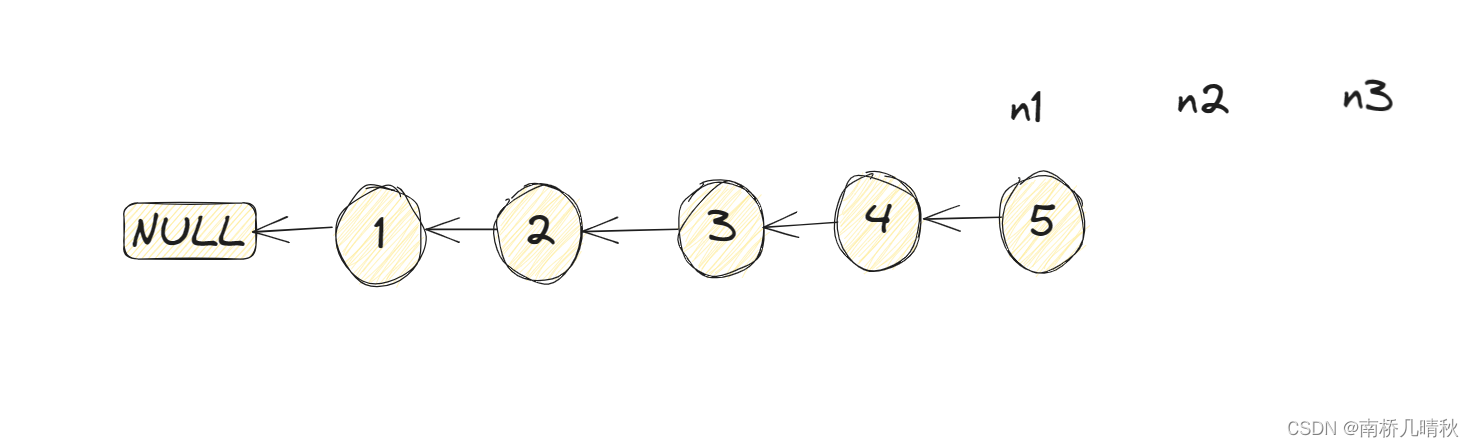
题目: 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:head [1,2] 输出:[2,1] 示例 3:…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...

Selenium 查找页面元素的方式
Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素,以下是主要的定位方式: 基本定位方式 通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...
