给定n个点或一个凸边形,求其最小外接矩形,可视化
这里写目录标题
- 原理
- 代码
原理
-
求n个点的最小外接矩形问题可以等价为先求这n个点的凸包,再求这个凸包的最小外接矩形。
其中求凸包可以使用Graham-Scan算法
需要注意的是,
因为Graham-Scan算法要求我们从先找到凸包上的一个点,所以我们可以先对这些点进行排序,根据x/y坐标都可以。排序后的第一个点和最后一点一定在凸包上。
同时,假设我们按照x排序,并且想要得到顺时针旋转的凸包边界,那么我们只能找到一半的边界,这是因为我们从左到右遍历这些点的时候只有上面的点才满足顺时针,下面的不可能满足顺时针(这里为了节省计算可以只对y坐标大于开始和结束点中最小y坐标的点进行计算)。
为了找到全部的点,我们需要正向判断完后再反向相同方法判断一遍。
这里为了判断是顺时针还是逆时针,我们使用的是两个方向叉乘的最后一项,从前一个方向转到后一个方向时:如果叉乘最后一项小于0,说明是顺时针旋转的(右手系)。
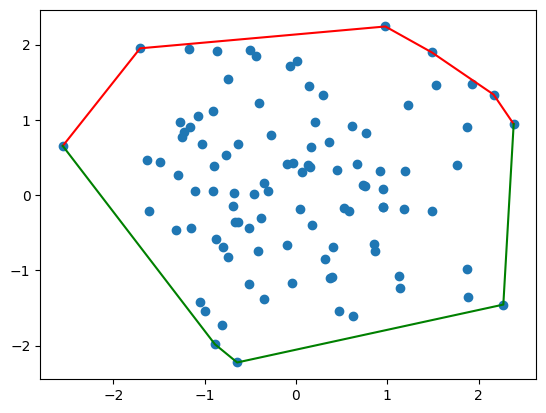
-
给定一个凸多边形,求最小外接矩形的原理可以参考这篇博客https://blog.csdn.net/wang_heng199/article/details/74477738
简单而言就是对凸包上的每条边构造矩形并比较面积。
我们这里的做法是遍历每条边,对于每条边,我们根据它与水平方向的夹角计算其旋转矩阵,并将这些凸包上的所有点根据此旋转矩阵的逆矩阵/转置矩阵(旋转矩阵是正交矩阵)旋转至水平方向,此时我们可以很容易得到这些点水平方向和竖直方向的边界点,从而就有了一个外接矩形。
代码
导入包并且初始化随机点:
import numpy as np
import matplotlib.pyplot as plt
n = 100
points = np.random.randn(n, 2)
计算凸包并可视化
sorted_points = points[np.argsort(points[:,0])]def cal_rotate_orientation(cur,stack_end,stack_end_before):'''计算p1->p2的向量旋转到p2->p3的向量是顺时针还是逆时针'''p1,p2,p3 = sorted_points[stack_end_before], sorted_points[stack_end], sorted_points[cur]x2,y2 = p3 - p2x1,y1 = p2 - p1return x1*y2 - x2*y1 #叉乘最后一项Z轴方向,<0:顺时针,>0:逆时针def cal_convex_hull(index_list):result = list(index_list[:2])index_list = index_list[2:]for i in index_list:if (cal_rotate_orientation(i,result[-1],result[-2]) < 0): #叉乘最后一项 ,符合顺时针# print(i,result[-1],result[-2])result.append(i)else:if len(result) == 2: result[-1] = i continueresult.pop()while(cal_rotate_orientation(i,result[-1],result[-2]) > 0): #不是顺时针,需要反复剔除result.pop()if len(result) < 2:breakresult.append(i)return result#n-1是最后一个点,因为它肯定在第一遍的结果里,所以两个结果合并时去除第一个
result = cal_convex_hull(range(0,n,1))+cal_convex_hull(range(n-1,-1,-1))[1:]
print(result)
#ploy是将结果按照顺序两两组合,形成边界
ploy = list(map(lambda i:result[i:i+2],range(0,len(result)-1)))plt.scatter(sorted_points[:, 0], sorted_points[:, 1])
plt.plot(sorted_points[result,0],sorted_points[result,1],color = 'red')
plt.show()
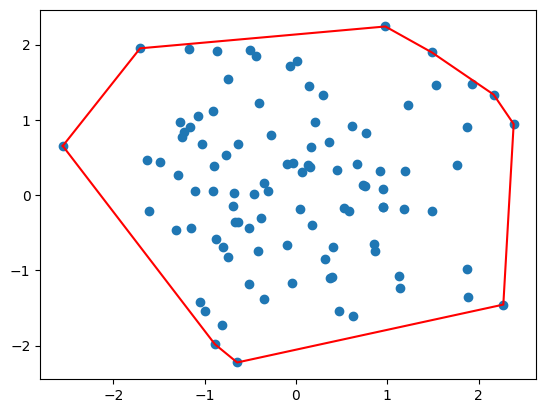
计算最小外接矩形
这里为了可视化,我们会将矩形转回来。
def get_rotate(cos,sin):#我们已知在原坐标系下的方向,要将其转化到目标系,用逆/转置return np.array([[cos,-sin],[sin,cos]]) def get_rotate2(theta):#我们已知在原坐标系下的方向,要将其转化到目标系,用逆/转置return np.array([[np.cos(theta),-np.sin(theta)],[np.sin(theta),np.cos(theta)]])row = 3
col = (len(ploy)+1)//3+1
fig, axs = plt.subplots(row, col, figsize=(15, 15))min_rect = [[],0,np.inf] #rect,angle,area
#假设是-90度 -> 90度
for idx, (i,j) in enumerate(ploy):x1,y1 = sorted_points[i]x2,y2 = sorted_points[j]tan_theta = (y2-y1)/(x2-x1)cos_theta = np.sqrt(1/(1+np.power(tan_theta,2)))sin_theta = cos_theta*tan_thetarotated_points = sorted_points@get_rotate(cos_theta,sin_theta)min_x,min_y = np.min(rotated_points,axis=0)max_x,max_y = np.max(rotated_points,axis=0)rect_xy = np.array([[min_x,min_y],[max_x,min_y],[max_x,max_y],[min_x,max_y]])rect_area = (max_x-min_x)*(max_y-min_y)if rect_area < min_rect[2]:min_rect = [rect_xy,np.arcsin(-sin_theta),rect_area] #这个角度是取反,因为要转回去rect_xy = rect_xy@get_rotate(cos_theta,-sin_theta) #转一下axs[idx//col,idx%col].scatter(points[:, 0], points[:, 1])plot_idx = [i for i in range(0,4)]+[0]axs[idx//col,idx%col].plot(rect_xy[plot_idx,0],rect_xy[plot_idx,1],color = 'orange')axs[idx//col,idx%col].set_xlim(-4,4)axs[idx//col,idx%col].set_ylim(-4,4)axs[idx//col,idx%col].set_aspect('equal')rect_xy = min_rect[0]@get_rotate2(min_rect[1])axs[(idx+1)//col,(idx+1)%col].scatter(points[:, 0], points[:, 1])
plot_idx = [i for i in range(0,4)]+[0]
axs[(idx+1)//col,(idx+1)%col].plot(rect_xy[plot_idx,0],rect_xy[plot_idx,1],color = 'red')
axs[(idx+1)//col,(idx+1)%col].set_xlim(-4,4)
axs[(idx+1)//col,(idx+1)%col].set_ylim(-4,4)
axs[(idx+1)//col,(idx+1)%col].set_aspect('equal')
plt.show()
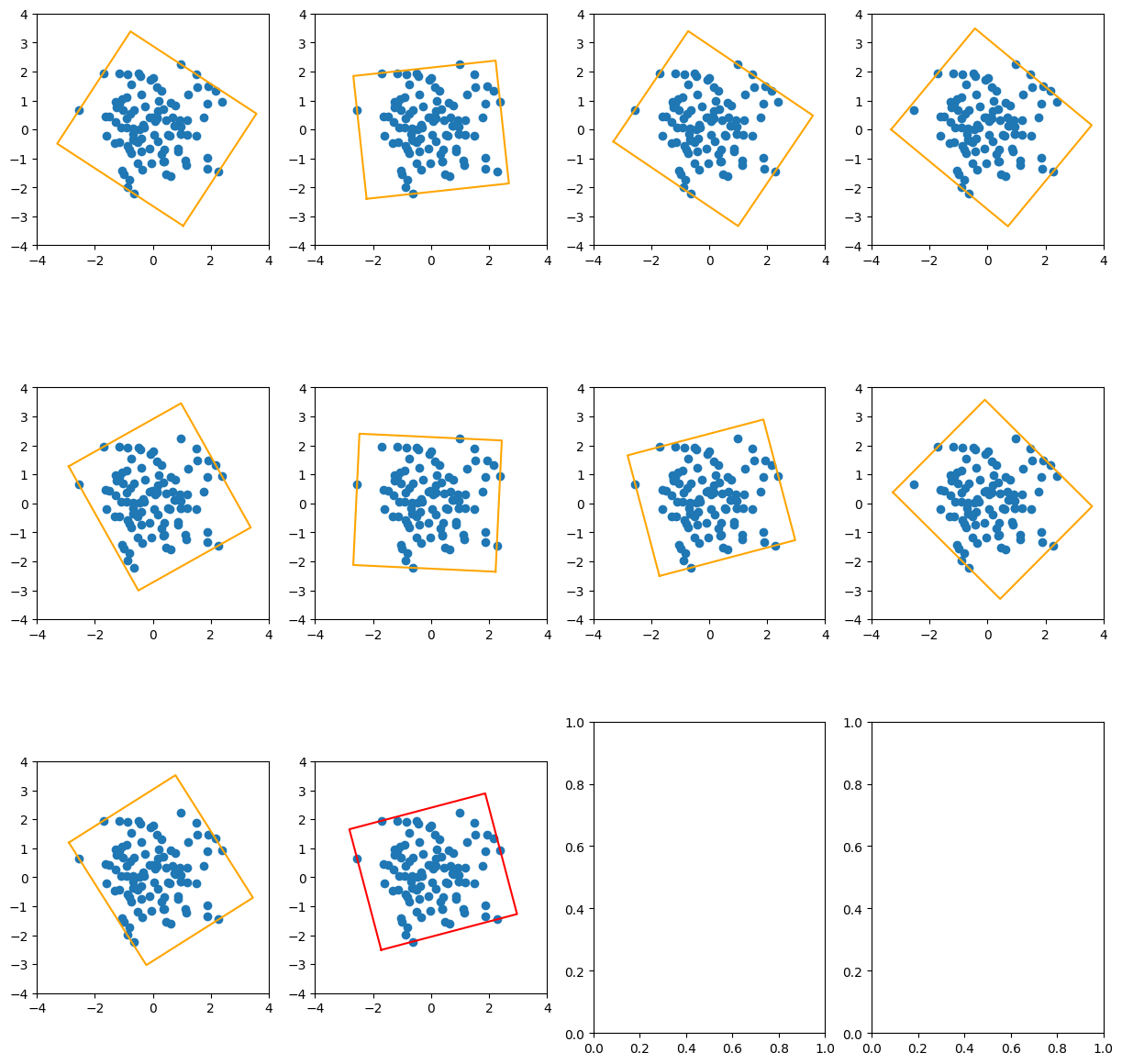
相关文章:

给定n个点或一个凸边形,求其最小外接矩形,可视化
这里写目录标题 原理代码 原理 求n个点的最小外接矩形问题可以等价为先求这n个点的凸包,再求这个凸包的最小外接矩形。 其中求凸包可以使用Graham-Scan算法 需要注意的是, 因为Graham-Scan算法要求我们从先找到凸包上的一个点,所以我们可以先…...

蓝桥杯每日一题2023.11.6
取位数 - 蓝桥云课 (lanqiao.cn) 题目描述 题目分析 由题意我们知道len中为现阶段长度,如果其与k相等也就是找到了正确的位数,否则就调用递归来进行搜索,每次搜索一位数。 #include <stdio.h> // 求x用10进制表示时的数位长度 int …...
V-REP和Python的联合仿真
机器人仿真软件 各类免费的的机器人仿真软件优缺点汇总_robot 仿真 软件收费么_dyannacon的博客-CSDN博客 课程地址 https://class.guyuehome.com/p/t_pc/course_pc_detail/column/p_605af87be4b007b4183a42e7 课程资料 guyueclass: 古月学院课程代码 旋转变换 旋转的左乘与…...

WPF布局控件之DockPanel布局
前言:博主文章仅用于学习、研究和交流目的,不足和错误之处在所难免,希望大家能够批评指出,博主核实后马上更改。 概述: DockPanel 位置子控件基于子 Dock 属性,你有 4 个选项停靠,左 (默认) &…...
【实战Flask API项目指南】之二 Flask基础知识
实战Flask API项目指南之 Flask基础知识 本系列文章将带你深入探索实战Flask API项目指南,通过跟随小菜的学习之旅,你将逐步掌握Flask 在实际项目中的应用。让我们一起踏上这个精彩的学习之旅吧! 前言 当小菜踏入Flask后端开发的世界&…...
C++链接库std::__cxx11::basic_string和std::__1::basic_string链接问题总结)
Linux 编译链接那些事儿(02)C++链接库std::__cxx11::basic_string和std::__1::basic_string链接问题总结
1 问题背景说明 在自己的项目源码中引用libeasysqlite.so时编译成功,但运行时遇到问题直接报错,找不到符号 symbol:_ZN3sql5FieldC1ENSt3__112basic_stringIcNS1_11char_traitsIcEENS1_9allocatorIcEEEENS_10field_typeEi。 2 问题描述和解…...
按键精灵中的UI界面操作
1. 按键精灵中UI界面常用的控件 1. 文字框 界面1: {标签页1:{文字框:{名称:"文字框1",显示内容:"显示内容",文字大小:0,高度:0,宽度:0,注释:"文字大小、高度、宽度是可选属性,如需使用默认值,可保持值为0或直接删除此属性&qu…...

dpdk 程序如何配置网卡收发包队列描述符配置?
问题描述 dpdk 程序在配置网卡队列时会涉及收发包队列描述符数量配置问题,收发包描述符的数量看似是一个简单的配置,却对转发性能有着一定的影响。实际业务程序中,收发包描述符大小配置一般参考 dpdk 内部示例程序配置进行,经验之…...

二蛋赠书七期:《云原生数据中台:架构、方法论与实践》
前言 大家好!我是二蛋,一个热爱技术、乐于分享的工程师。在过去的几年里,我一直通过各种渠道与大家分享技术知识和经验。我深知,每一位技术人员都对自己的技能提升和职业发展有着热切的期待。因此,我非常感激大家一直…...
计算机毕设 基于大数据的服务器数据分析与可视化系统 -python 可视化 大数据
文章目录 0 前言1 课题背景2 实现效果3 数据收集分析过程**总体框架图****kafka 创建日志主题****flume 收集日志写到 kafka****python 读取 kafka 实时处理****数据分析可视化** 4 Flask框架5 最后 0 前言 🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升&a…...
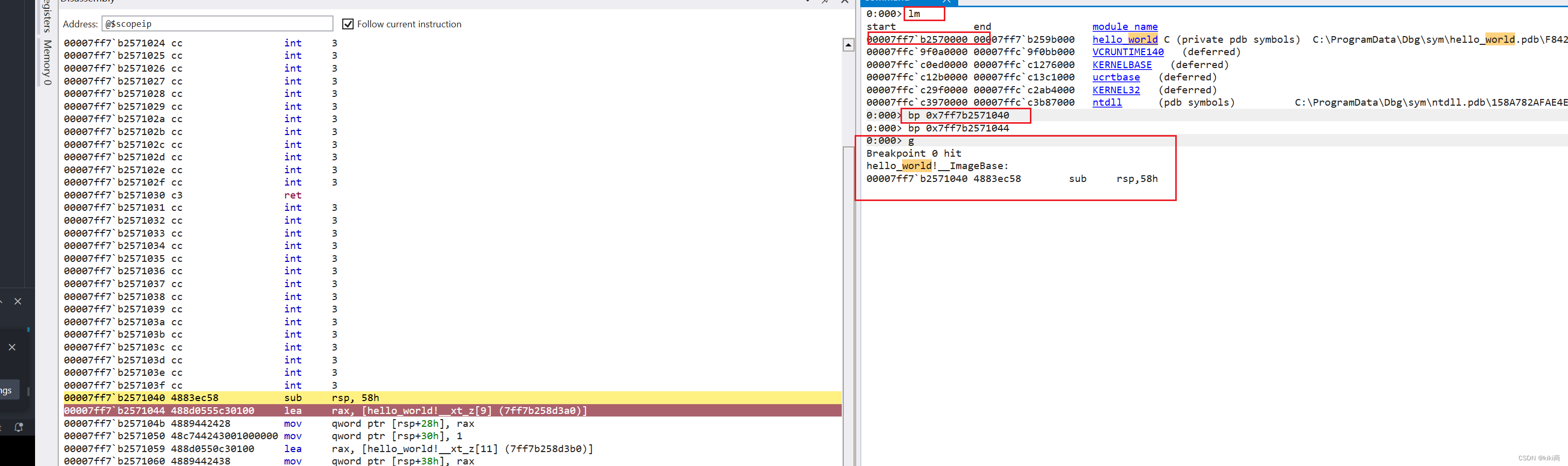
初识rust
调试下rust 的执行流程 参考: 认识 Cargo - Rust语言圣经(Rust Course) 新建一个hello world 程序: fn main() {println!("Hello, world!"); }用IDA 打开exe,并加载符号: 根据字符串找到主程序入口: 双击…...
shiro-cve2016-4437漏洞复现
一、漏洞特征 Apache Shiro是一款开源强大且易用的Java安全框架,提供身份验证、授权、密码学和会话管理。Shiro框架直观、易用,同时也能提供健壮的安全性。 因为在反序列化时,不会对其进行过滤,所以如果传入恶意代码将会造成安全问题 在 1.2.4 版本前, 加…...
【MongoDB-Redis-MySQL-Elasticsearch-Kibana-RabbitMQ-MinIO】Java全栈开发软件一网打尽
“Java全栈开发一网打尽:在Windows环境下探索技术世界的奇妙之旅” 前言 全栈开发是一项复杂而令人兴奋的任务,涵盖了从前端到后端、数据库到可视化层、消息队列到文件存储的广泛领域。本文将带您深入探讨在Windows环境下进行全栈开发的过程࿰…...

Implementing class错误解决
最近在使用IDEASmart Tomcat启动项目时,报以下错误: Injection of resource dependencies failed; nested exception is java.lang.IncompatibleClassChangeError: Implementing class根据网上结论加上我这里的原因,总共以下几个方面&#x…...
关于 国产系统UOS系统Qt开发Tcp服务器外部连接无法连接上USO系统 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/134254817 红胖子(红模仿)的博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软…...
初阶JavaEE(15)(Cookie 和 Session、理解会话机制 (Session)、实现用户登录网页、上传文件网页、常用的代码片段)
接上次博客:初阶JavaEE(14)表白墙程序-CSDN博客 Cookie 和 Session 你还记得我们之前提到的Cookie吗? Cookie是HTTP请求header中的一个属性,是一种用于在浏览器和服务器之间持久存储数据的机制,允许网站…...

C++入门学习(1)命名空间和输入输出
前言 在C语言和基本的数据结构学习之后,我们终于迎来了期待已久的C啦!C发明出来的意义就是填补一些C语言的不足,让我们更加方便的写代码,所以今天我们就来讲一下C语言不足的地方和在C中的解决办法! 一、命名空间 在学习…...

AI:58-基于深度学习的猫狗图像识别
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌在这个漫长的过程,中途遇到了不少问题,但是…...
【原创】java+swing+mysql宠物领养管理系统设计与实现
摘要: 生活中,有很多被人遗弃的宠物,这些宠物的处理成为了一个新的难题。生活中也有许多人喜欢养宠物,为了方便大家进行宠物领养,提高宠物领养管理的效率和便利性。本文针对这一问题,提出设计和实现一个基…...

虚拟机Linux-Centos系统网络配置常用命令+Docker 的常用命令
目录 1、虚拟机Linux-Centos系统网络配置常用命令2、Docker 的常用命令2.1 安装docker步骤命令2.2 在docker容器中安装和运行mysql 2、dockerfile关键字区别(ADD/COPY,CMD/ENTRYPOINT) 1、虚拟机Linux-Centos系统网络配置常用命令 进入网络配置文件目录 cd /etc/sysconfig/ne…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...

Spring事务传播机制有哪些?
导语: Spring事务传播机制是后端面试中的必考知识点,特别容易出现在“项目细节挖掘”阶段。面试官通过它来判断你是否真正理解事务控制的本质与异常传播机制。本文将从实战与源码角度出发,全面剖析Spring事务传播机制,帮助你答得有…...
