[100天算法】-第一个错误的版本(day 62)
题目描述
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。假设你有 n 个版本 [1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。示例:给定 n = 5,并且 version = 4 是第一个错误的版本。调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true所以,4 是第一个错误的版本。来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/first-bad-version
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方法1:二分法
思路
寻找最左边的满足条件的值
框架:
- 首先定义搜索区间为 [left, right],左右都闭合。
- 循环搜索条件为 left <= right,只要区间内有元素就继续寻找。
- 循环体内,我们不断更新 mid ,并判断 mid 是否符合题目要求。
- 如果 mid 符合要求,我们找到了一个备胎, 接着收缩右边界,继续看看左边还有没有。
- 否则收缩左边界,去右侧寻找。
- 最后我们定点到 left 元素上,由于不会提前返回,因此我们需要检查最终的 left 是否符合要求。
- 如果不符合题目要求,或者 left 出了右边的边界,说明没有找到,返回 -1。
- 否则返回 left 即可。
复杂度
- 时间复杂度:$O(logn)$
- 空间复杂度:$O(1)$
代码
Python Code
# The isBadVersion API is already defined for you. # @param version, an integer # @return a bool # def isBadVersion(version):class Solution(object):def firstBadVersion(self, n):""":type n: int:rtype: int"""l, r, m = 1, n, 0while l <= r:m = l + (r - l) // 2if isBadVersion(m): r = m - 1else: l = m + 1return l# 本题中“错误版本”一定存在,不然还是需要检查最终的左指针# return l if l <= n and isBadVersion(l) else -1
相关文章:
)
[100天算法】-第一个错误的版本(day 62)
题目描述 你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。假设你有 n 个版本 [1, 2, ..., n],你…...

React 学习系列: 类组件生命周期方法
类组件生命周期方法 constructor 在类组件挂载的时候调用,用于构建一个类组件实例。 在构建类组件实例的时候, 会先执行基类构造函数( React.Component ) 使用父组件传入的 props 来初始化 props 属性, 然后执行自定义构造函数来初始化 state…...
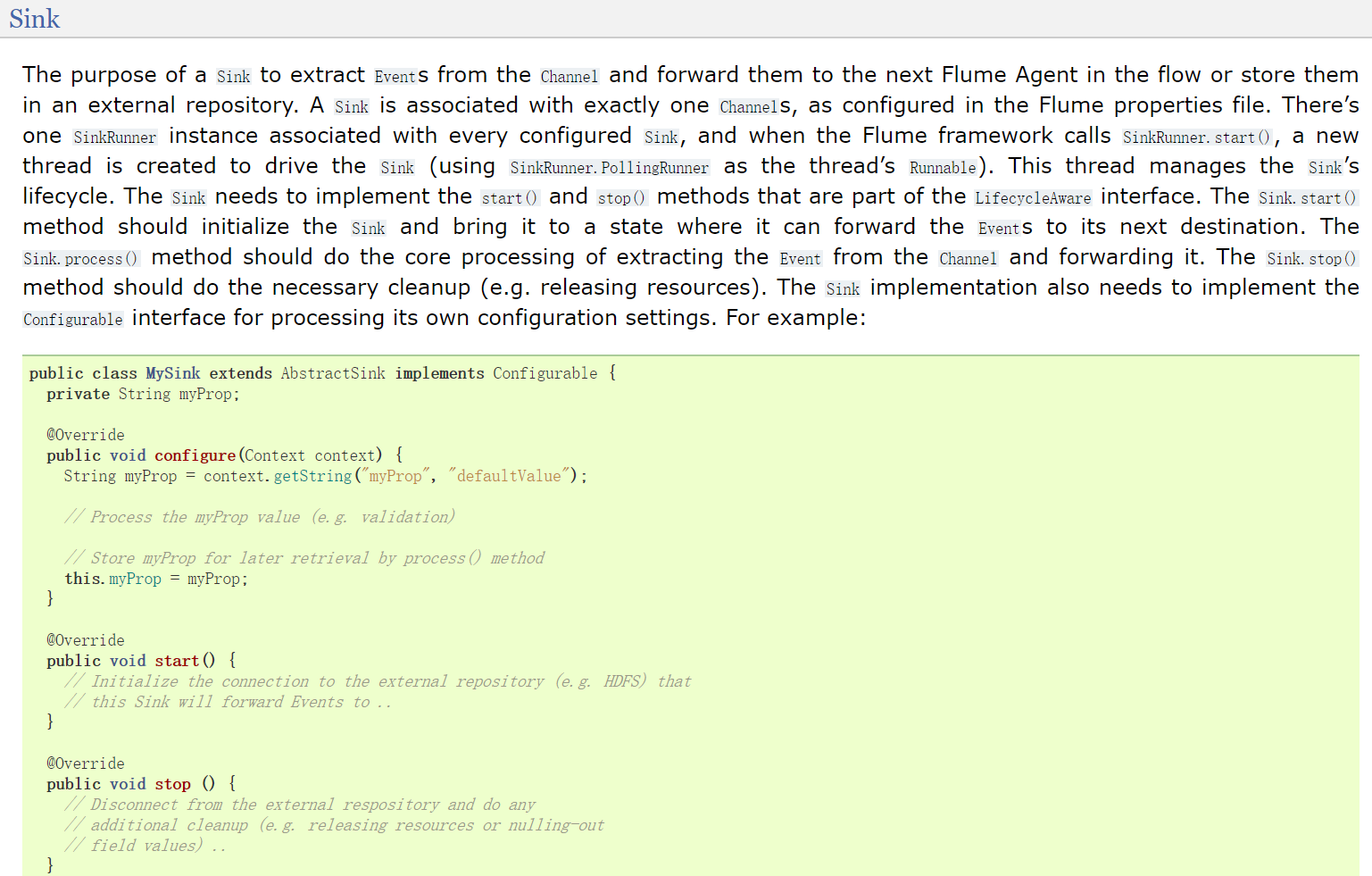
Flume从入门到精通一站式学习笔记
文章目录 什么是FlumeFlume的特性Flume高级应用场景Flume的三大核心组件Source:数据源channelsink Flume安装部署Flume的使用案例:采集文件内容上传至HDFS案例:采集网站日志上传至HDFS 各种自定义组件例如:自定义source例如&#…...
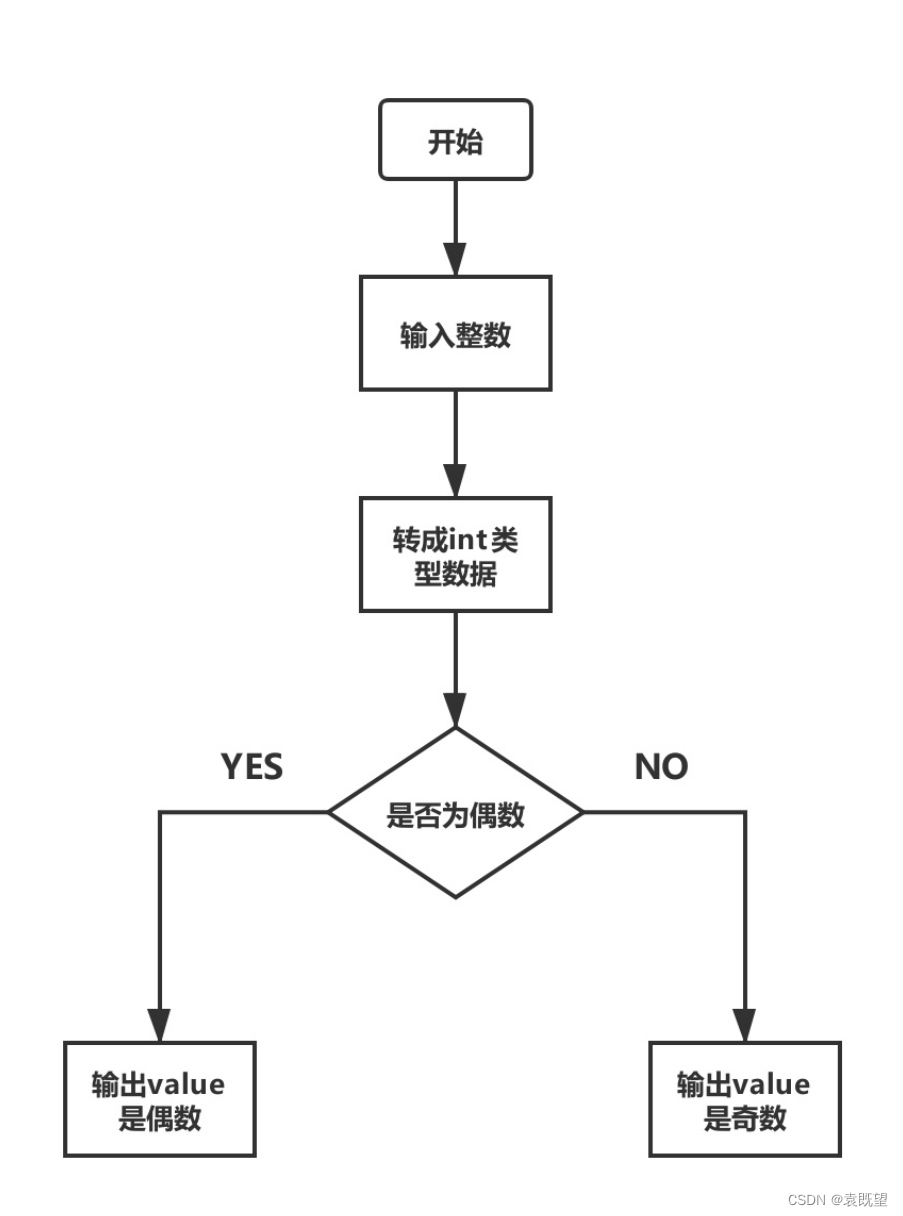
Python150题day08
2.基础语法篇 2.1 if 条件句 ①单个条件分支 使用input函数接收用户的输入,如果用户输入的整数是偶数,则使用print函数输出"你输入的整数是:{value],它是偶数”,[value]部分要替换成用户的输入。 解答: value input("请输⼊⼀…...

正则表达式的修饰符
正则表达式的修饰符是用来修改和调整正则表达式的特殊字符或元字符。修饰符可以改变正则表达式的行为和匹配方式。以下是一些常见的正则表达式修饰符: g(全局):表示全局匹配,即在整个字符串中搜索所有匹配项ÿ…...
从行车记录仪恢复已删除/丢失视频的方法
“我的车里有行车记录仪。几天前,当我下班回家时,一辆卡车不知从哪里冒出来撞向了我。我们的两辆车都损坏了,但幸运的是,没有人受伤。我曾与卡车司机就修理我的汽车进行过会面,但他说我有错。我需要查看我的行车记录仪…...

TypeScript_抓取酒店价格数据
我们导入所需的库,包括http和request。然后,我们定义一个函数,该函数接受一个URL作为参数。 import http from http; import request from request;const fetchHotelPrices (url: string) > {// ... }接下来,我们使用request…...
vue前端实现多个url下载并合并为zip文件
一、安装 npm install jszip npm install file-saver 二、引入 import axios from axios import JSZip from "jszip"; import FileSaver from "file-saver"; 三、核心代码 videoData:[/video/26519f026fc012521605563015227403.mp4,/video/f7b9cdae14…...
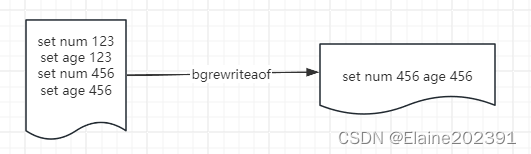
Redis02-持久化策略
目录 RDB(Redis DataBase Backup file) RDB执行原理 AOF(Append-Only File) RDB和AOF对比 Redis支持多种持久化方式,以确保数据在内存中持久存储,以便在Redis服务器重启时数据不会丢失。Redis中持久化的…...
Crypto(9)[MRCTF2020]keyboard
下载题目,看看里面是什么 这是什么鬼,由题目可以获得线索,keyboard,不是键盘吗,然后看了看别人写的wp,发现是九键,有几个数字对应的密文就是第几个字母 比如第一个6,对应的字母是mno,…...

IOS自带的OCR识别功能
一、识别身份证 interface IDCardScanViewController () <AVCaptureMetadataOutputObjectsDelegate> property (nonatomic, strong) AVCaptureSession *captureSession; end implementation IDCardScanViewController - (void)viewDidLoad { [super viewDidLoad…...

1300*C. Product of Three Numbers(质数数学)
Problem - 1294C - Codeforces 解析: 首先这个数肯定不是质数,然后找到第一个因子p,对于n/p再判断质数,然后找到另外两个因子即可。 注意三个因子不能相同。 #include<bits/stdc.h> using namespace std; #define int long…...
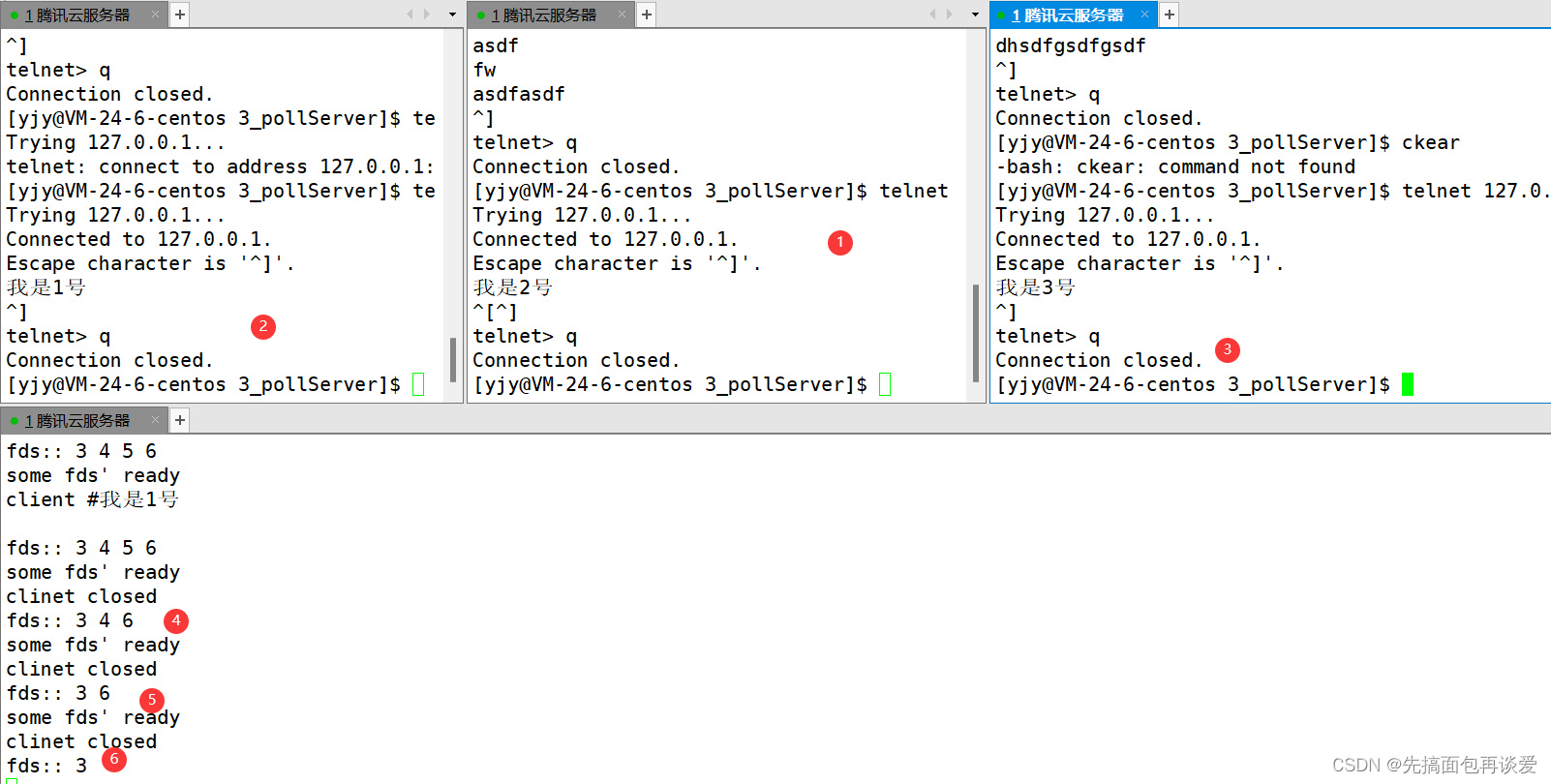
【网络】五中IO模型介绍 + 多路转接中select和poll服务器的简单编写
高级IO 前言正式开始前面的IO函数简单过一遍什么叫做低效的IO钓鱼的例子同步IO和异步IO五种IO模型阻塞IO非阻塞IO信号驱动多路转接异步IO 小结 代码演示非阻塞IO多路转接select介绍简易select服务器timeout 为 nullptrtimeout 为 {0, 0}timeout 为 {5, 0}调用accept select编写…...

Camtasia2024破解版电脑屏幕录制剪辑软件
屏幕录制剪辑 TechSmith Camtasia for Mac v2021是 TechSmith 公司所开发出一款专业屏幕录像和编辑, Camtasia Studio2024版是由TechSmith公司官方进行汉化推出的最新版本,除2023版以下版本均没有官方汉化。 同时TechSmith公司打击第三方贩卖Camtasia Studio汉化的…...
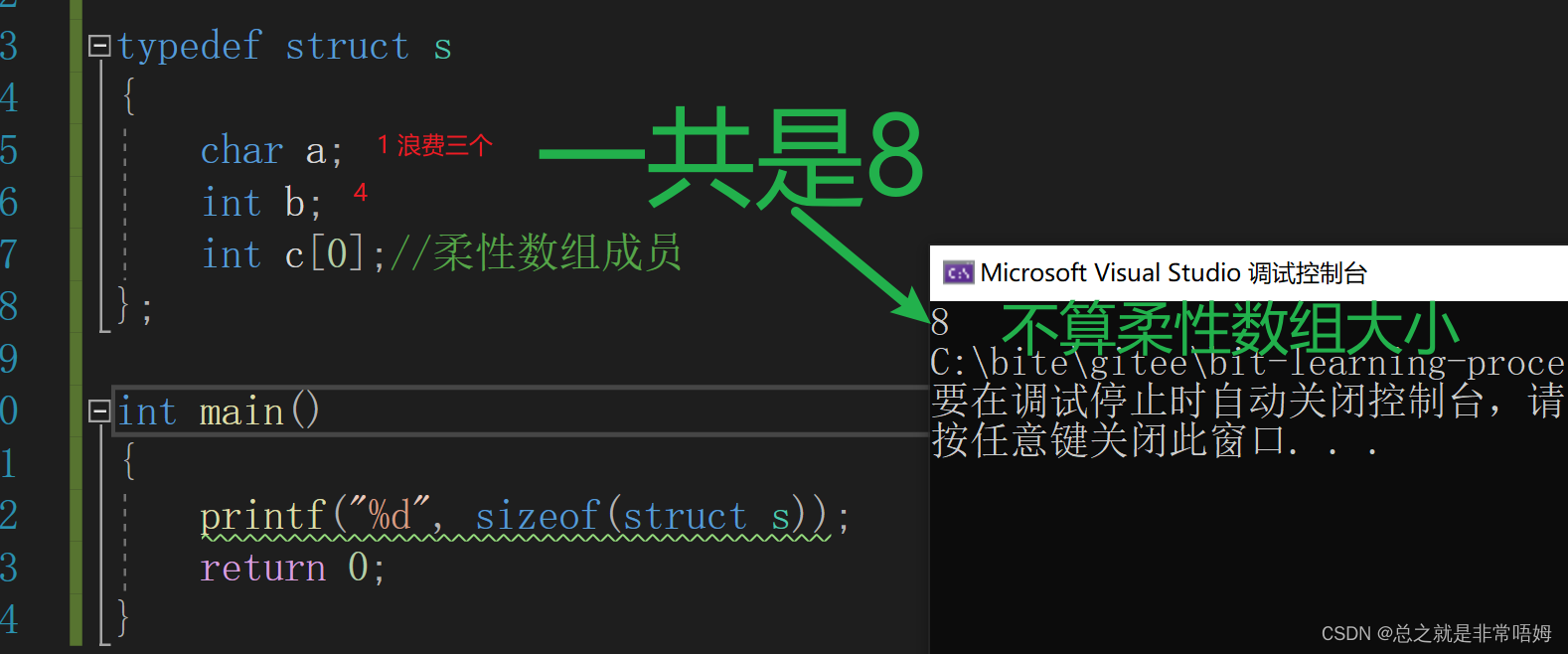
c语言进阶部分详解(《高质量C-C++编程》经典例题讲解及柔性数组)
上篇文章我介绍了介绍动态内存管理 的相关内容:c语言进阶部分详解(详细解析动态内存管理)-CSDN博客 各种源码大家可以去我的github主页进行查找:唔姆/比特学习过程2 (gitee.com) 今天便接“上回书所言”,来介绍《高质…...

Unreal PythonScriptPlugin
Unreal PythonScriptPlugin 文章目录 Unreal PythonScriptPluginPython vs UnLua官方文档PyStubDoString 示例代码,引擎里有很多插件已经用 py 写编辑器脚本了 unreal.get_editor_subsystem(unreal.LevelEditorSubsystem).load_level("/Game/maps/UVlayoutTes…...

什么是数据可视化,为什么数据可视化很重要?
数据可视化是数据的图形表示,可以帮助人们更轻松地理解和解释复杂的信息。它涉及创建数据的视觉表示,例如图表、图形、地图和其他视觉元素,以传达数据中的见解、模式和趋势。数据可视化是将原始数据转化为可操作知识的关键工具。 以下是数据…...

chatgpt相关问题解答
1. openAI的chatgpt的收费方式有哪几种? 根据OpenAI官方的信息,ChatGPT的收费方式包括两种: 1.订阅计划(Subscription Plan):OpenAI提供了ChatGPT Plus订阅计划,每月收费20美元。订阅计划的用…...
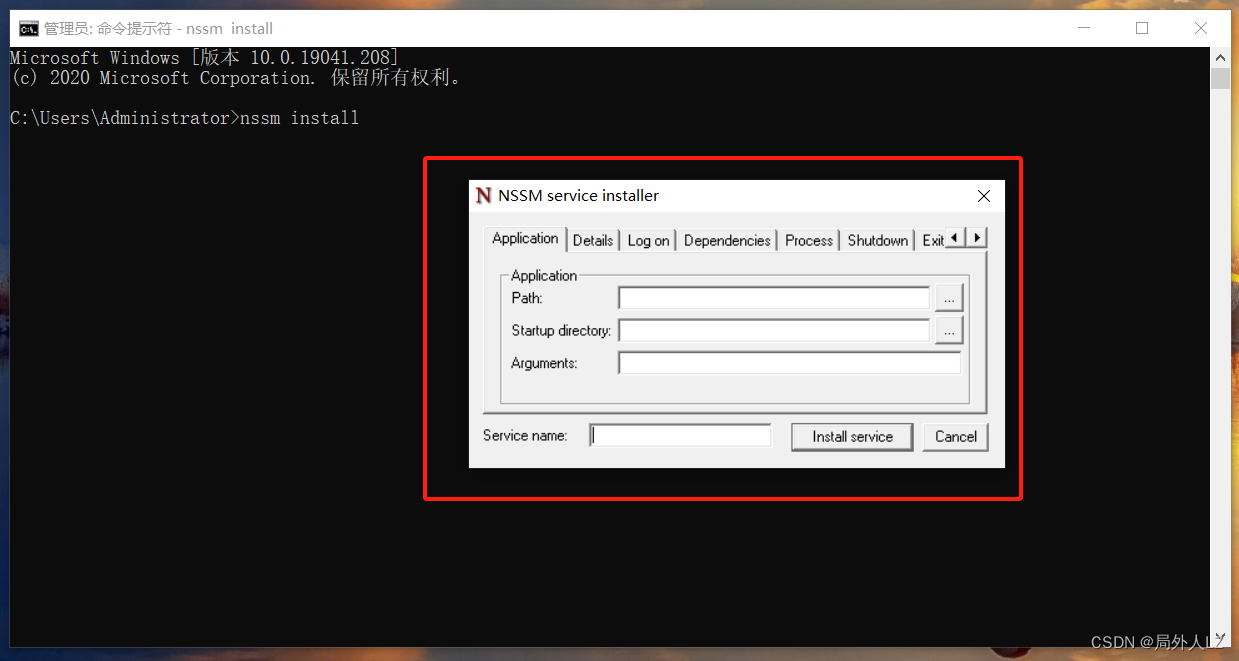
nssm将exe应用封装成windows服务
一、简介 NSSM(Non-Sucking Service Manager)是一个用于在Windows操作系统上管理和运行应用程序作为服务的工具。它提供了一种简单的方法来将任意可执行文件转换为Windows服务,并提供了一些额外的功能和配置选项。 优点: 简单易…...

golang实现极简todolist
ToDoList 最近跟着qimi老师做了一个ToDoList,我做的GitHub地址贴在这里,但由于前端出了点问题,所以都是用postman进行测试 原项目地址 部分功能展示 删除代办 查找代办 下面给出思路 思路 其实这是一个很简单的增删改查的实现ÿ…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
