[PyTorch][chapter 61][强化学习-免模型学习1]
前言:
在现实的学习任务中,环境
其中的转移概率P,奖赏函数R 是未知的,或者状态X也是未知的
称为免模型学习(model-free learning)
目录:
1: 蒙特卡洛强化学习
2:同策略-蒙特卡洛强化学习
3: 异策略- 蒙特卡洛强化学习
一 蒙特卡洛强化学习
在免模型学习的情况下,策略迭代算法会遇到两个问题:
1: 是策略无法评估
因为无法做全概率展开。此时 只能通过在环境中执行相应的动作观察得到的奖赏和转移的状态、
解决方案:一种直接的策略评估代替方法就是“采样”,然后求平均累积奖赏,作为期望累积奖赏的近似,这称为“蒙特卡罗强化学习”。
2: 策略迭代算法估计的是 状态值函数(state value function) V,而最终的策略是通过 状态 动作值函数(state-action value function) Q 来获得。
模型已知时,有很简单的从 V 到 Q 的转换方法,而模型未知 则会出现困难。
解决方案:所以我们将估计对象从 V 转为 Q,即:估计每一对 “状态-动作”的值函数。
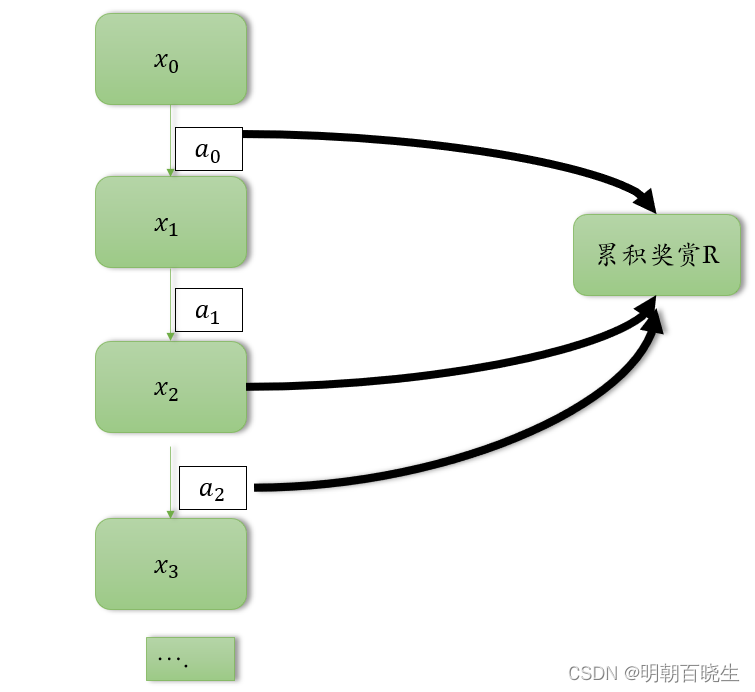
模型未知的情况下,我们从起始状态出发,使用某种策略进行采样,执行该策略T步,
并获得轨迹 ,
然后 对轨迹中出现的每一对 状态-动作,记录其后的奖赏之和,作为 状态-动作 对的一次
累积奖赏采样值. 多次采样得到多条轨迹后,将每个状态-动作对的累积奖赏采样值进行平均。即得到 状态-动作值函数的估计.
二 同策略蒙特卡洛强化学习
要获得好的V值函数估计,就需要不同的采样轨迹。
我们将确定性的策略 称为原始策略
原始策略上使用 -贪心法的策略记为
以概率
选择策略1: 策略1 :
以概率
选择策略2: 策略2:均匀概率选取动作,
对于最大化值函数的原始策略
其中贪心策略
中:
当前最优动作被选中的概率
每个非最优动作选中的概率 ,多次采样后将产生不同的采样轨迹。
因此对于最大值函数的原始策略,同样有

算法中,每采样一条轨迹,就根据该轨迹涉及的所有"状态-动作"对值函数进行更新
同策略蒙特卡罗强化学习算法最终产生的是E-贪心策略。然而,引入E-贪心策略是为了便于策略评估,而不是最终使用
三 同策略蒙特卡洛算法 Python
# -*- coding: utf-8 -*-
"""
Created on Fri Nov 3 09:37:32 2023@author: chengxf2
"""# -*- coding: utf-8 -*-
"""
Created on Thu Nov 2 19:38:39 2023@author: cxf
"""import random
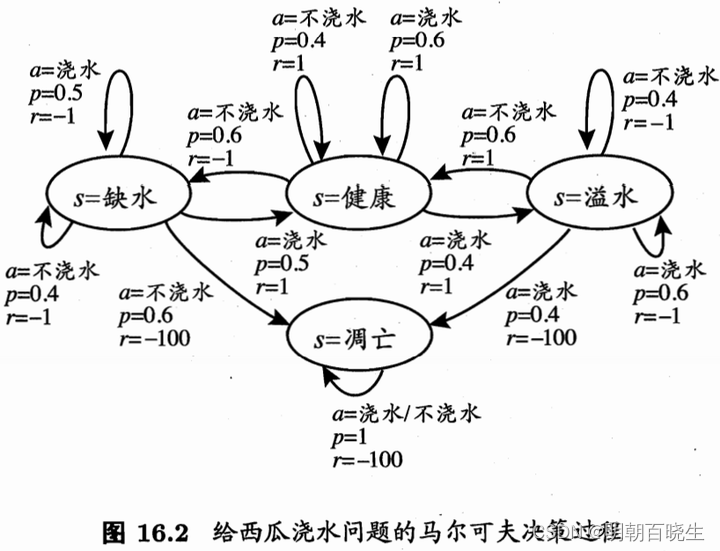
from enum import Enumclass State(Enum):'''状态空间X'''shortWater =1 #缺水health = 2 #健康overflow = 3 #溢水apoptosis = 4 #凋亡class Action(Enum):'''动作空间A'''water = 1 #浇水noWater = 2 #不浇水class Env():def reward(self, nextState):r = -100if nextState is State.shortWater:r =-1elif nextState is State.health:r = 1elif nextState is State.overflow:r= -1else:r = -100return rdef action(self, state, action):if state is State.shortWater:#print("\n state--- ",state, "\t action---- ",action)if action is Action.water :S =[State.shortWater, State.health]proba =[0.5, 0.5]else:S =[State.shortWater, State.apoptosis]proba =[0.4, 0.6]elif state is State.health:#健康if action is Action.water :S =[State.health, State.overflow]proba =[0.6, 0.4]else:S =[State.shortWater, State.health]proba =[0.6, 0.4]elif state is State.overflow:#溢水if action is Action.water :S =[State.overflow, State.apoptosis]proba =[0.6, 0.4]else:S =[State.health, State.overflow]proba =[0.6, 0.4]else: #凋亡S =[State.apoptosis]proba =[1.0]#print("\n S",S, "\t prob ",proba)nextState = random.choices(S, proba)[0]r = self.reward(nextState)#print("\n nextState ",nextState,"\t reward ",r)return nextState,rdef __init__(self):self.X = Noneclass Agent():def initPolicy(self):self.Q ={}self.count ={}brandom = True #使用随机策略for state in self.S:for action in self.A:self. Q[state, action] = 0self.count[state,action]= 0randProb= [0.5,0.5]return self.Q, self.count, randProb,brandomdef randomPolicy(self,randProb,T):A = self.Aenv = Env()state = State.shortWater #从缺水开始history =[]for t in range(T):a = random.choices(A, randProb)[0]nextState,r = env.action(state, a)item = [state,a,r,nextState]history.append(item)state = nextStatereturn historydef runPolicy(self,policy,T):env = Env()state = State.shortWater #从缺水开始history =[]for t in range(T):action = policy[state]nextState,r = env.action(state, action)item = [state,action,r,nextState]history.append(item)state = nextStatereturn historydef getTotalReward(self, t,T, history):denominator =T -ttotalR = 0.0for i in range(t,T):#列表下标为0 开始,所以不需要t+1r= history[i][2]totalR +=rreturn totalR/denominatordef updateQ(self, t ,history,R):#[state,action,r,nextState]state = history[t][0]action = history[t][1]count = self.count[state,action]self.Q[state, action]= (self.Q[state,action]*count+R)/(count+1)self.count[state,action] = count+1def learn(self):Q,count,randProb,bRandom =self.initPolicy()T =10policy ={}for s in range(1,self.maxIter): #采样第S 条轨迹if bRandom: #使用随机策略history = self.randomPolicy(randProb, T)#print(history)else:print("\n 迭代次数 %d"%s ,"\t 缺水:",policy[State.shortWater].name,"\t 健康:",policy[State.health].name,"\t 溢水:",policy[State.overflow].name,"\t 凋亡:",policy[State.apoptosis].name)history = self.runPolicy(policy, T)#已经有了一条轨迹了for t in range(0,T-1):R = self.getTotalReward(t, T, history)self.updateQ(t, history, R)rand = random.random()if rand < self.epsilon: #随机策略执行bRandom = Trueelse:bRandom = Falsefor state in self.S:maxR = self.Q[state, self.A[0]]for action in self.A:r = self.Q[state,action]if r>=maxR:policy[state] = actionmaxR = rreturn policydef __init__(self):self.S = [State.shortWater, State.health, State.overflow, State.apoptosis]self.A = [Action.water, Action.noWater]self.Q ={}self.count ={}self.policy ={}self.maxIter =5self.epsilon = 0.2if __name__ == "__main__":agent = Agent()agent.learn()相关文章:

[PyTorch][chapter 61][强化学习-免模型学习1]
前言: 在现实的学习任务中,环境 其中的转移概率P,奖赏函数R 是未知的,或者状态X也是未知的 称为免模型学习(model-free learning) 目录: 1: 蒙特卡洛强化学习 2:同策略-蒙特卡洛强化学习 3&am…...

网络运维Day04-补充
文章目录 周期性计划任务周期性计划任务使用案例一案例二 周期性计划任务 在固定时间可以完成相同的任务,被称之为周期性计划任务由crond服务提供需要将定时任务,写到一个文件书写格式如下 分 时 日 月 周 任务(绝对路径)分:0-59时ÿ…...
前端埋点方式
前言: 想要了解用户在系统中所做的操作,从而得出用户在本系统中最常用的模块、在系统中停留的时间。对于了解用户的行为、分析用户的需求有很大的帮助,想实现这种需求可以通过前端埋点的方式。 埋点方式: 1.什么是埋点?…...

iOS导航栏返回按钮
导航栏返回按钮隐藏: override func pushViewController(_ viewController: UIViewController, animated: Bool) {if let vc self.viewControllers.last {let backItem UIBarButtonItem()backItem.title ""vc.navigationItem.backBarButtonItem backI…...
2023中国视频云市场报告:腾讯云音视频解决方案份额连续六次蝉联榜首,加速全球化布局
近日,国际数据公司(IDC)发布了《中国视频云市场跟踪(2023上半年)》报告,腾讯云音视频的解决方案份额连续六次蝉联榜首,并在视频生产创作与媒资管理市场份额中排名第一。同时,在实时音…...

jpa Repository的常用写法总结
一、前言 之前项目在xml中写sql,感觉标签有很多,比较灵活; 最近在写新项目,使用了jpa,只能在java中写sql了,感觉不太灵活,但是也得凑付用。 以下总结下常用入参出参写法。 二、Repository代…...
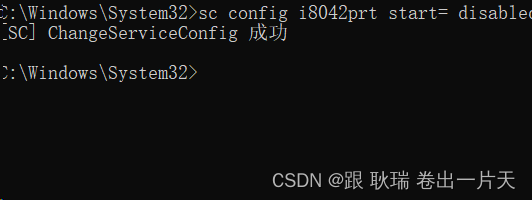
笔记本电脑 禁用/启用 自带键盘
现在无论办公还是生活 很多人都会选择笔记本电脑 但很多人喜欢机械键盘 或者 用一些外接键盘 但是很多时候我们想操作 会碰到笔记本原来的键盘导致错误操作 那么 我们就需要将笔记本原来的键盘禁用掉 我们先以管理员身份运行命令窗口 然后 有两个命令 禁用默认键盘 sc conf…...
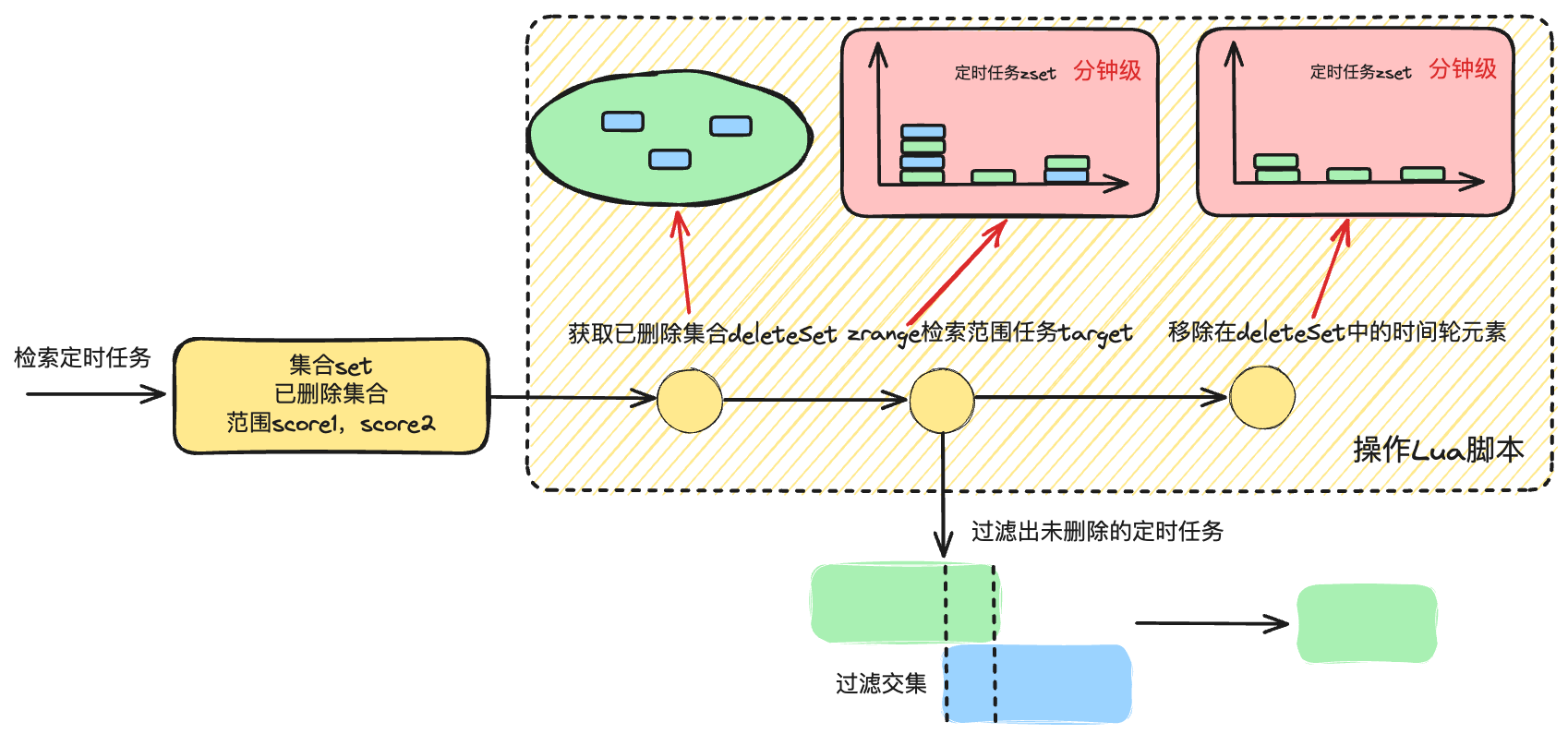
基于 golang 从零到一实现时间轮算法 (三)
引言 本文参考小徐先生的相关博客整理,项目地址为: https://github.com/xiaoxuxiansheng/timewheel/blob/main/redis_time_wheel.go。主要是完善流程以及记录个人学习笔记。 分布式版实现 本章我们讨论一下,如何基于 redis 实现分布式版本的…...
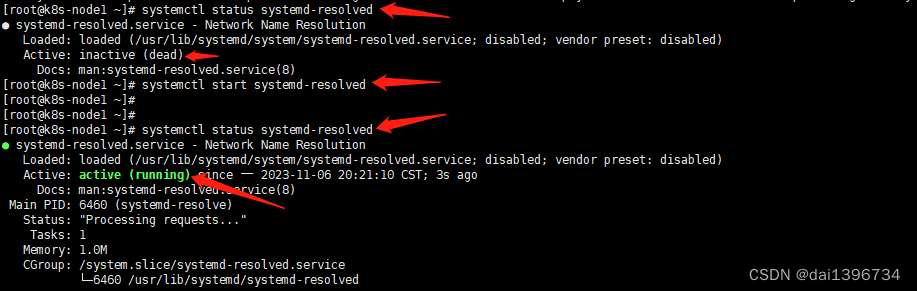
k8s 1.28安装
容器运行时,containerd 按照官方的指导,需要安装runc和cni插件,提示的安装方式,有三种: 二进制安装包源码apt-get 或 dnf安装 我们这里选用第三种,找到docker官方提供的安装方式 ubuntu-containerd # A…...
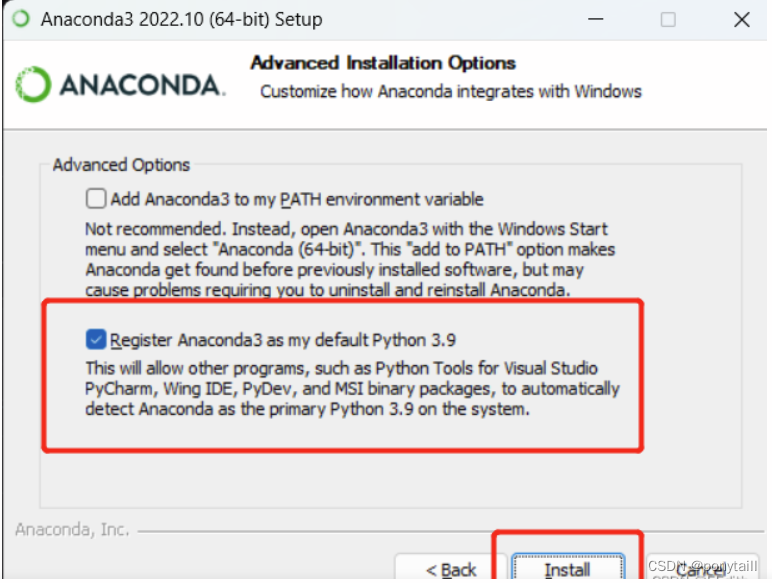
安装anaconda时控制台conda-version报错
今天根据站内的一篇博客教程博客在此安装anaconda时,检查conda版本时报错如下: >>>>>>>>>>>> ERROR REPORT <<<<<<<<<<<< Traceback (most recent call last): File “D:\An…...
链表(1)
目录 单链表 主函数test.c test1 test2 test3 test4 头文件&函数声明SList.h 函数实现SList.c 打印SLPrint 创建节点CreateNode 尾插SLPushBack 头插SLPushFront 头删SLPopBck 尾删SLPopFront 易错点 本篇开始链表学习。今天主要是单链表&OJ题目。 单链…...
智慧农业:农林牧数据可视化监控平台
数字农业是一种现代农业方式,它将信息作为农业生产的重要元素,并利用现代信息技术进行农业生产过程的实时可视化、数字化设计和信息化管理。能将信息技术与农业生产的各个环节有机融合,对于改造传统农业和改变农业生产方式具有重要意义。 图扑…...
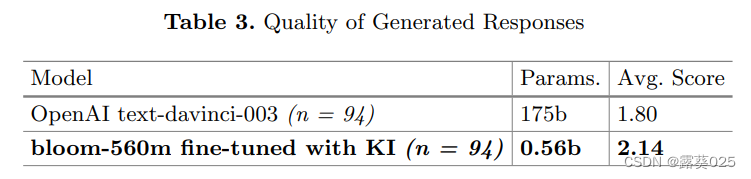
知识注入以对抗大型语言模型(LLM)的幻觉11.6
知识注入以对抗大型语言模型(LLM)的幻觉 摘要1 引言2 问题设置和实验2.1 幻觉2.2 生成响应质量 3 结果和讨论3.1 幻觉3.2 生成响应质量 4 结论和未来工作 摘要 大型语言模型(LLM)内容生成的一个缺点是产生幻觉,即在输…...

机器人物理交互场景及应用的实际意义
机器人物理交互场景是指机器人与物理世界或人类进行实际的物理互动和交互的情境。这些场景涉及机器人在不同环境和应用中使用其物理能力,以执行任务、提供服务或与人类互动。 医疗协助: 外科手术助手:机器人可以用于外科手术,提供…...
Kubernetes Dashboard 用户名密码方式登录
Author:rab 前言 为了 K8s 集群安全,默认情况下 Dashboard 以 Token 的形式登录的,那如果我们想以用户名/密码的方式登录该怎么操作呢?其实只需要我们创建用户并进行 ClusterRoleBinding 绑定即可,接下来是具体的操作…...

Redisson中的对象
Redisson - 是一个高级的分布式协调Redis客服端,能帮助用户在分布式环境中轻松实现一些Java的对象 (Bloom filter, BitSet, Set, SetMultimap, ScoredSortedSet, SortedSet, Map, ConcurrentMap, List, ListMultimap, Queue, BlockingQueue, Deque, BlockingDeque, …...

GNU ld链接器 lang_process()(二)
一、ldemul_create_output_section_statements() 位于lang_process()中11行 。 该函数用于创建与目标有关的输出段的语句。这些语句将用于描述输出段的属性和分配。 void ldemul_create_output_section_statements (void) {if (ld_emulation->create_output_section_sta…...
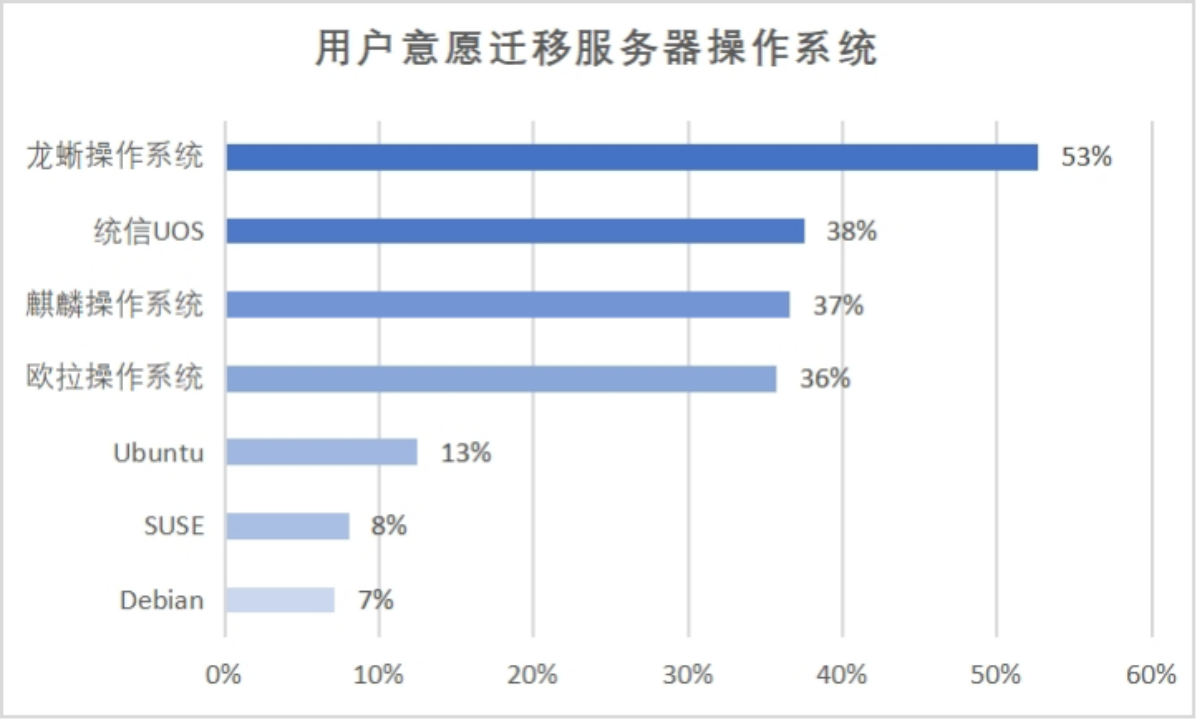
《国产服务器操作系统发展报告(2023)》重磅发布
11月1日,《国产服务器操作系统发展报告(2023)》(以下简称“报告”)在 2023 云栖大会上正式发布,开放原子开源基金会理事长孙文龙、中国信息通信研究院副总工程师石友康、阿里云基础软件部副总裁马涛、浪潮信…...
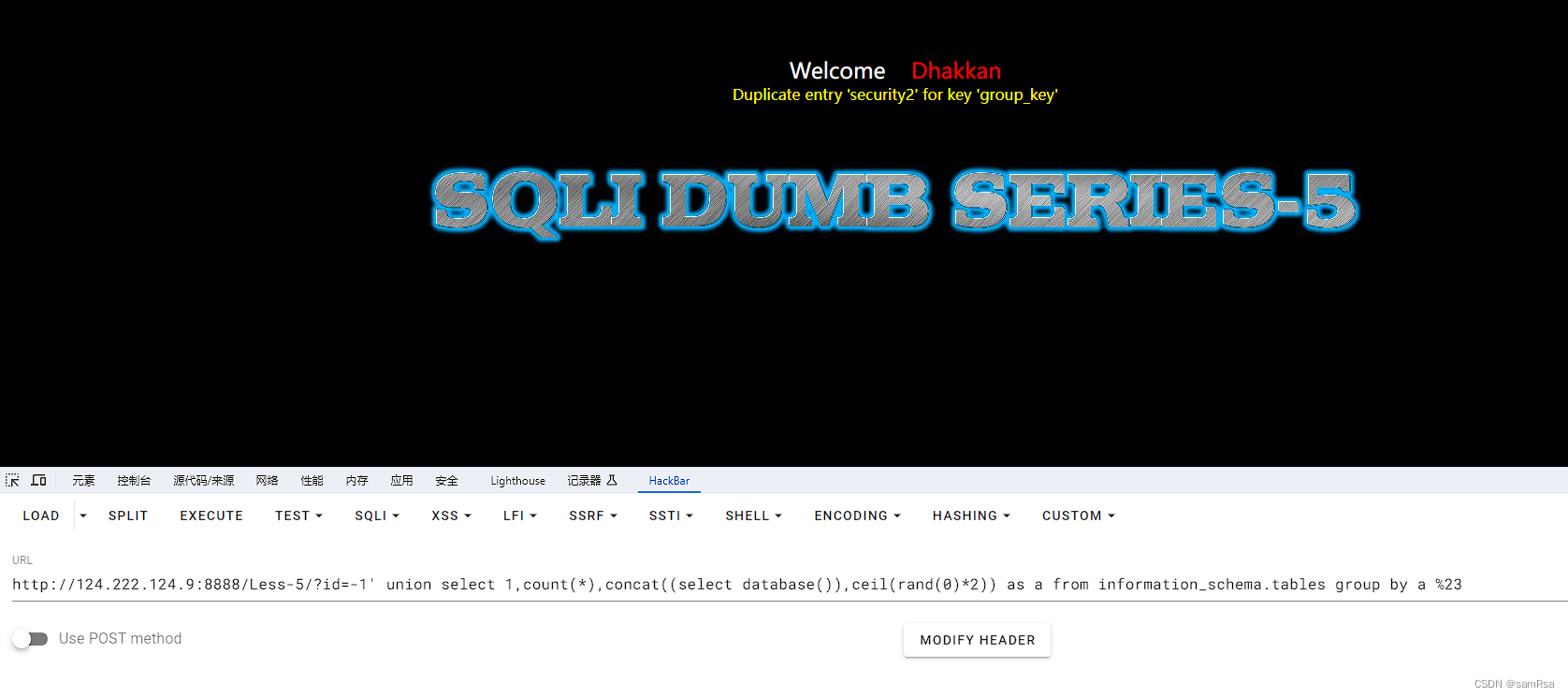
【PTE-day03 报错注入】
报错注入 1、报错注入 group by count2、报错注入 extractvalue3、报错注入updatexml1、报错注入 group by count http://124.222.124.9:8888/Less-5/?id=-1 union select 1,count(*),concat((select database()),ceil(rand(0)*2)) as a from information_schema.tables grou…...
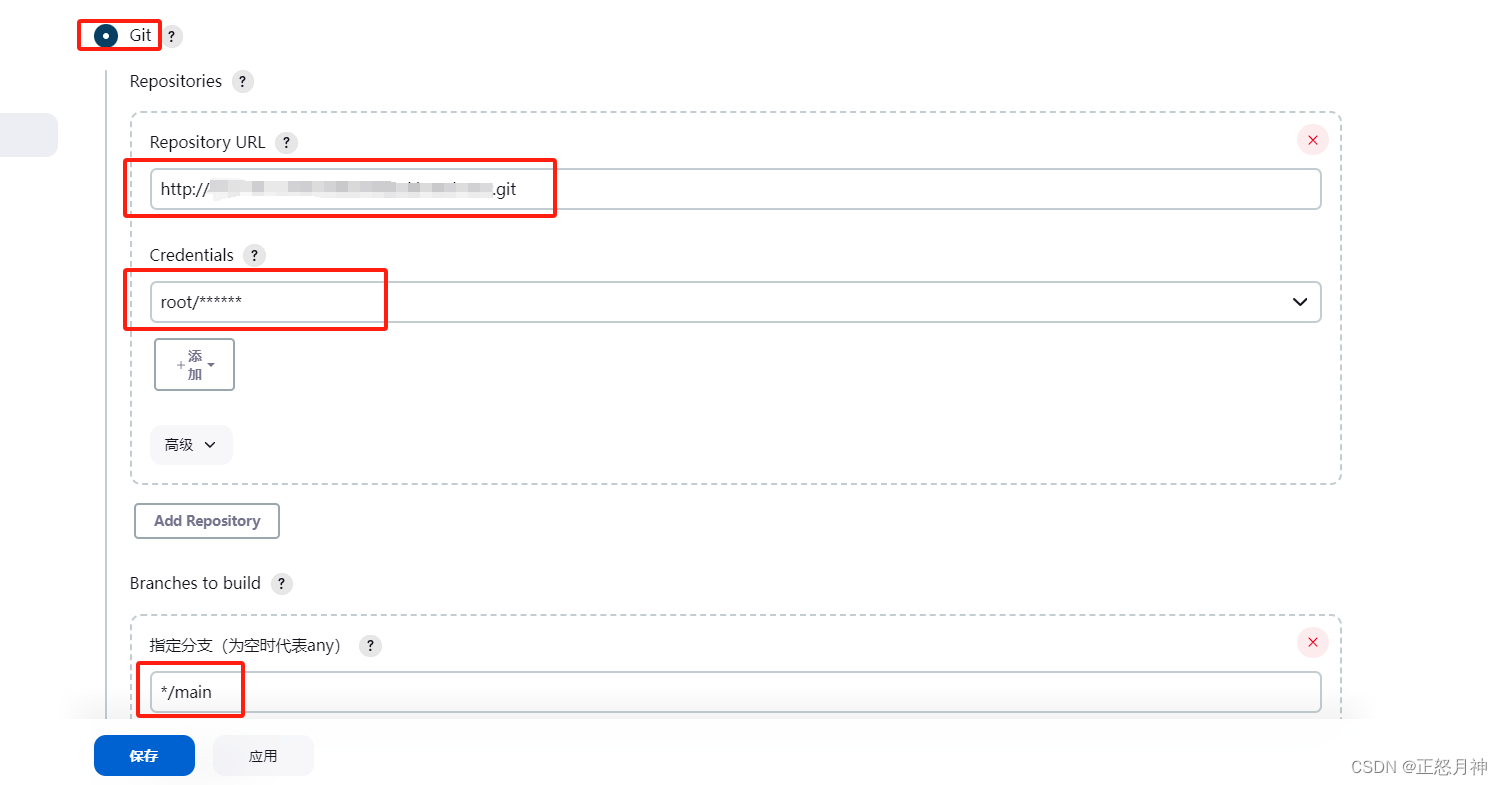
jenkins gitlab CI/CD
jenkins的安装教程就不说了:Jenkins docker 一键发布 (一)_jenkins 一键发布-CSDN博客 最近打算从svn切换到gitlab,所以配置了一下jenkins的git 很简单,直接上图 1 选择 Git 2 录入gitlab的http地址(由于我的git地址不是22端口&…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
