Python每日一练(20230227)

目录
1. 路径交叉 ★★★
2. 缺失的第一个正数 ★★★
3. 寻找两个正序数组的中位数 ★★★
附录
散列表
基本概念
常用方法
1. 路径交叉
给你一个整数数组 distance 。
从 X-Y 平面上的点 (0,0) 开始,先向北移动 distance[0] 米,然后向西移动 distance[1] 米,向南移动 distance[2] 米,向东移动 distance[3] 米,持续移动。也就是说,每次移动后你的方位会发生逆时针变化。
判断你所经过的路径是否相交。如果相交,返回 true ;否则,返回 false 。
示例 1:
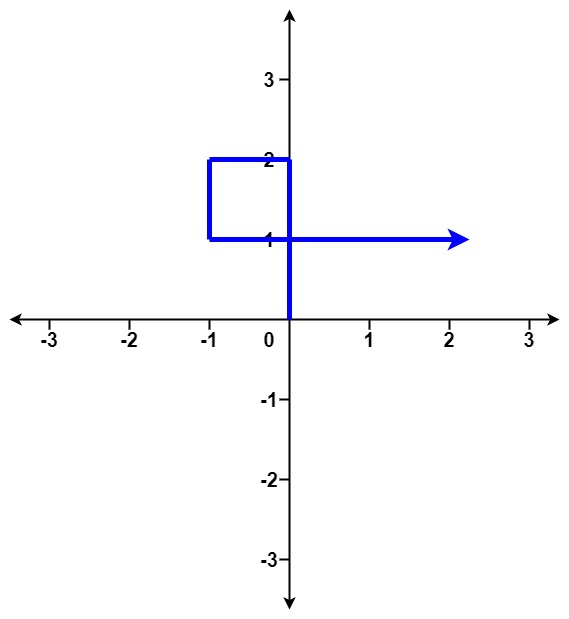
输入:distance = [2,1,1,2] 输出:true
示例 2:
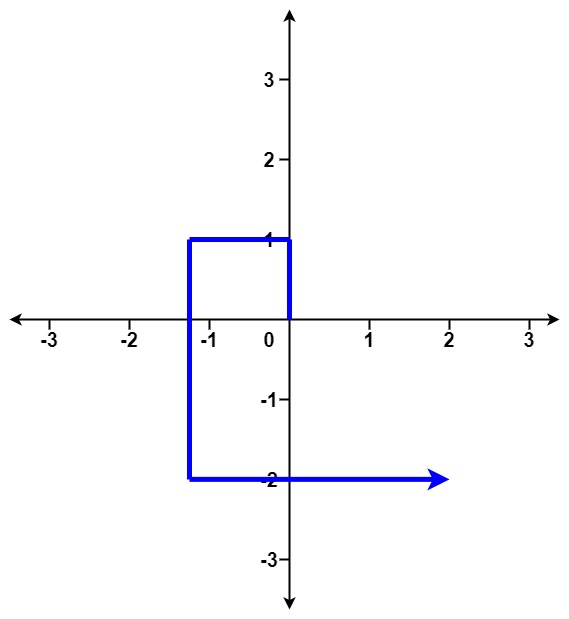
输入:distance = [1,2,3,4] 输出:false
示例 3:
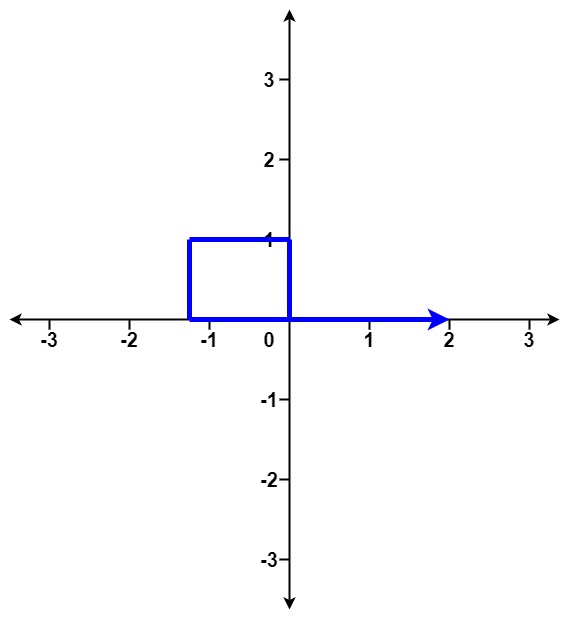
输入:distance = [1,1,1,1] 输出:true
提示:
1 <= distance.length <= 1051 <= distance[i] <= 105
代码:
class Solution:def isSelfCrossing(self, x: list) -> bool:n = len(x)if n < 3: return Falsefor i in range(3, n):if x[i] >= x[i - 2] and x[i - 3] >= x[i - 1]: return Trueif i >= 4 and x[i - 3] == x[i - 1] and x[i] / x[i - 4] >= x[i - 2]: return Trueif i >= 5 and x[i - 3] >= x[i - 1] and x[i - 2] >= x[i - 4] and x[i - 1] + x[i - 5] >= x[i - 3] and x[i] + x[i - 4] >= x[i - 2]: return Truereturn Falses = Solution()
distance = [2,1,1,2]
print(s.isSelfCrossing(distance))distance = [1,2,3,4]
print(s.isSelfCrossing(distance))distance = [1,1,1,1]
print(s.isSelfCrossing(distance))输出:
True
False
True
2. 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
进阶:你可以实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案吗?
示例 1:
输入:nums = [1,2,0] 输出:3
示例 2:
输入:nums = [3,4,-1,1] 输出:2
示例 3:
输入:nums = [7,8,9,11,12] 输出:1
提示:
0 <= nums.length <= 300-2^31 <= nums[i] <= 2^31 - 1
代码:
class Solution(object):def firstMissingPositive(self, nums):ls = len(nums)index = 0while index < ls:if nums[index] <= 0 or nums[index] > ls or nums[nums[index] - 1] == nums[index]:index += 1else:pos = nums[index] - 1nums[index], nums[pos] = nums[pos], nums[index]res = 0while res < ls and nums[res] == res + 1:res += 1return res + 1# %%
s = Solution()
print(s.firstMissingPositive(nums = [1,2,0]))
print(s.firstMissingPositive(nums = [3,4,-1,1]))
print(s.firstMissingPositive(nums = [7,8,9,11,12]))输出:
3
2
1
3. 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
示例 1:
输入:nums1 = [1,3], nums2 = [2] 输出:2.00000 解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4] 输出:2.50000 解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
示例 3:
输入:nums1 = [0,0], nums2 = [0,0] 输出:0.00000
示例 4:
输入:nums1 = [], nums2 = [1] 输出:1.00000
示例 5:
输入:nums1 = [2], nums2 = [] 输出:2.00000
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-10^6 <= nums1[i], nums2[i] <= 10^6
代码:
import math
from typing import Listclass Solution:def findMedianSortedArrays(self, nums1: List[int],nums2: List[int]) -> float:nums1Size = len(nums1)nums2Size = len(nums2)na = nums1Size + nums2Sizens = []i = 0j = 0m = int(math.floor(na / 2 + 1))while len(ns) < m:n = Noneif i < nums1Size and j < nums2Size:if nums1[i] < nums2[j]:n = nums1[i]i += 1else:n = nums2[j]j += 1elif i < nums1Size:n = nums1[i]i += 1elif j < nums2Size:n = nums2[j]j += 1ns.append(n)d = len(ns)if na % 2 == 1:return ns[d - 1]else:return (ns[d -1] + ns[d - 2]) / 2.0# %%
s = Solution()
print(s.findMedianSortedArrays([1,3], [2]))
print(s.findMedianSortedArrays([1,2], [3,4]))
print(s.findMedianSortedArrays([0,0], [0,0]))
print(s.findMedianSortedArrays([], [1]))
print(s.findMedianSortedArrays([2], []))输出:
2
2.5
0.0
1
2
附录
散列表
Hash table,也叫哈希表,是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
给定表M,存在函数f(key),对任意给定的关键字值key,代入函数后若能得到包含该关键字的记录在表中的地址,则称表M为哈希(Hash)表,函数f(key)为哈希(Hash) 函数。
基本概念
若关键字为k,则其值存放在f(k)的存储位置上。由此,不需比较便可直接取得所查记录。称这个对应关系f为散列函数,按这个思想建立的表为散列表。
对不同的关键字可能得到同一散列地址,即k1≠k2,而f(k1)==f(k2),这种现象称为冲突(英语:Collision)。具有相同函数值的关键字对该散列函数来说称做同义词。综上所述,根据散列函数f(k)和处理冲突的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或散列,所得的存储位置称散列地址。
若对于关键字集合中的任一个关键字,经散列函数映象到地址集合中任何一个地址的概率是相等的,则称此类散列函数为均匀散列函数(Uniform Hash function),这就是使关键字经过散列函数得到一个“随机的地址”,从而减少冲突。
常用方法
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快地定位。实际工作中需视不同的情况采用不同的哈希函数,通常考虑的因素有:
· 计算哈希函数所需时间
· 关键字的长度
· 哈希表的大小
· 关键字的分布情况
· 记录的查找频率
1.直接寻址法:
取关键字或关键字的某个线性函数值为散列地址。即H(key)=key或H(key) = a·key + b,其中a和b为常数(这种散列函数叫做自身函数)。若其中H(key)中已经有值了,就往下一个找,直到H(key)中没有值了,就放进去。
2. 数字分析法:
分析一组数据,比如一组员工的出生年月日,这时我们发现出生年月日的前几位数字大体相同,这样的话,出现冲突的几率就会很大,但是我们发现年月日的后几位表示月份和具体日期的数字差别很大,如果用后面的数字来构成散列地址,则冲突的几率会明显降低。因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。
3. 平方取中法:
当无法确定关键字中哪几位分布较均匀时,可以先求出关键字的平方值,然后按需要取平方值的中间几位作为哈希地址。这是因为:平方后中间几位和关键字中每一位都相关,故不同关键字会以较高的概率产生不同的哈希地址。
4. 折叠法:
将关键字分割成位数相同的几部分,最后一部分位数可以不同,然后取这几部分的叠加和(去除进位)作为散列地址。数位叠加可以有移位叠加和间界叠加两种方法。移位叠加是将分割后的每一部分的最低位对齐,然后相加;间界叠加是从一端向另一端沿分割界来回折叠,然后对齐相加。
5. 随机数法:
选择一随机函数,取关键字的随机值作为散列地址,即H(key)=random(key)其中random为随机函数,通常用于关键字长度不等的场合。
6. 除留余数法:
取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 H(key) = key MOD p,p≤m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。对p的选择很重要,一般取素数或m,若p选的不好,容易产生同义词。
相关文章:

Python每日一练(20230227)
目录 1. 路径交叉 ★★★ 2. 缺失的第一个正数 ★★★ 3. 寻找两个正序数组的中位数 ★★★ 附录 散列表 基本概念 常用方法 1. 路径交叉 给你一个整数数组 distance 。 从 X-Y 平面上的点 (0,0) 开始,先向北移动 distance[0] 米,然后向西移…...

Scratch少儿编程案例-算法练习-存款收益计算
专栏分享 点击跳转=>Unity3D特效百例点击跳转=>案例项目实战源码点击跳转=>游戏脚本-辅助自动化点击跳转=>Android控件全解手册点击跳转=>Scratch编程案例👉关于作者...

【Linux驱动开发100问】Linux驱动开发工程师在面试中常被问到的问题汇总
🥇今日学习目标:什么是Kconfig?如何使用Kconfig? 🤵♂️ 创作者:JamesBin ⏰预计时间:10分钟 🎉个人主页:嵌入式悦翔园个人主页 🍁专栏介绍:Lin…...

每日学术速递2.27
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CL 1.FiTs: Fine-grained Two-stage Training for Knowledge-aware Question Answering 标题:FiTs:用于知识感知问答的细粒度两阶段训练 作者:Qichen…...

【数据库系统概论】基础知识总结
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...
)
简单移动平均在量化中的应用(附Python实战代码)
在大多数金融产品的投资过程中,均线系统都是很重要的投资参考。一般来说,均线可以近似理解为某段时间内成交筹码的均价,它往往能帮助我们找到合适的支撑位和压力位。随着各种技术流派以及统计学的发展,从简单移动平均中逐渐衍生出了更多的均线计算方式,比如指数移动平均、…...
ChatGPT提高你日常工作的五个特点,以及如何使用它来提高代码质量
ChatGPT已经完全改变了代码开发模式。然而,大多数软件开发者和数据专家们仍然不使用ChatGPT来完善——并简化他们的工作。 这就是我们在这里列出提升日常工作效率和质量的5个不同的特点的原因。 让我们一起来看看在日常工作中如何使用他们。 警告:不要…...

spark datasourceV1和v2
datasourceV2 一文理解 Apache Spark DataSource V2 诞生背景及入门实战 https://zhuanlan.zhihu.com/p/83006243 2.3 Data source API v2 https://issues.apache.org/jira/browse/SPARK-15689 Because of the above limitations/issues, the built-in data source impleme…...
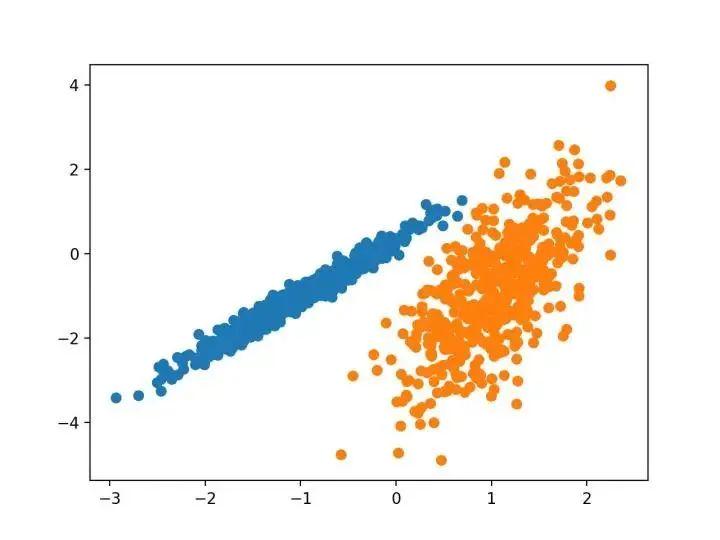
10种聚类算法的完整python操作示例
大家好,聚类或聚类分析是无监督学习问题。它通常被用作数据分析技术,用于发现数据中的有趣模式,例如基于其行为的客户群。有许多聚类算法可供选择,对于所有情况,没有单一的最佳聚类算法。相反,最好探索一系…...

构建合作伙伴生态系统刻不容缓
合作伙伴关系管理(PRM)系统是否已死?向合作伙伴生态系统的转变将如何改变我们未来管理合作伙伴计划的方式? 自PC革命以来,间接销售和渠道营销一直普遍存在于技术领域,通过其他公司的销售团队和人脉来增加销售,是一种明…...
)
剑指 Offer 55 - I. 二叉树的深度(java解题)
剑指 Offer 55 - I. 二叉树的深度(java解题)1. 题目2. 解题思路3. 数据类型功能函数总结4. java代码1. 题目 输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径&a…...
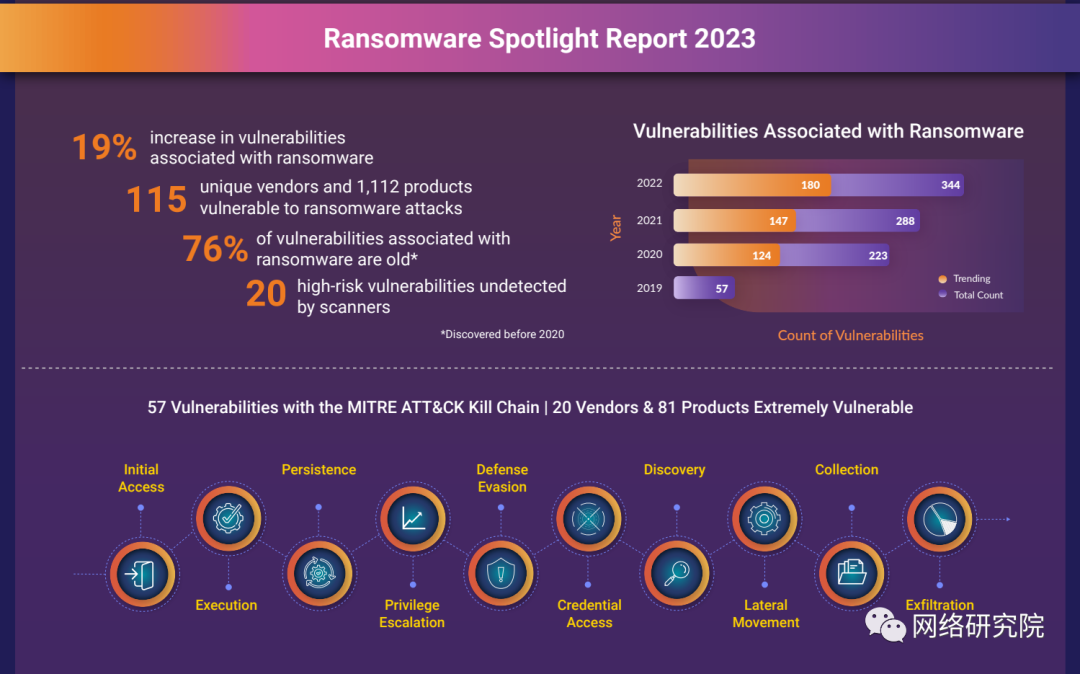
威胁行为者将旧漏洞武器化以发起勒索软件攻击
勒索软件运营商比以往任何时候都更加依赖未打补丁的系统来获得对受害者网络的初始访问权限。 一份新报告显示,攻击者正在互联网和暗网中积极搜索可用于勒索软件攻击的旧漏洞和已知漏洞。 其中许多缺陷已存在多年,对尚未修补或更新易受攻击系统的组织构…...

2023北京健博会/第十届中国国际大健康产博览会
China-DJK北京健博会,立足北京打造国内外大健康产业快速融合发展平台; 大健康时代:20年前没有健康产业,如今健康产业成了全球经济中唯“不缩水”的行业,早已被国际经济学界确定为“无限广阔的兆亿产业”。据机构数据&…...
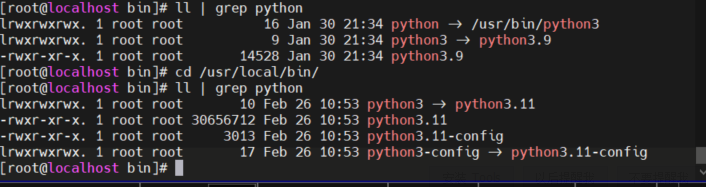
Python学习笔记之环境搭建
Python学习笔记之环境搭建1. 下载Python2. Windows 安装最新Python3. Linux 安装最新PythonPython是一种编程语言,可以让您更快地工作并更有效地集成系统。 您可以学习使用Python,并立即看到生产力的提高和维护成本的降低。 Python是荷兰程序员吉多范罗苏…...

死锁的总结
哲学家死锁造成的原因:我有你需要的,但你已经有了 饥饿与死锁的区别 死锁一旦发生一定又饥饿现象,但是饥饿现象产生不一定是死锁 历史上对于死锁的声音 死锁的方案 前面两个都是不允许死锁出现 前面都是概念性的东西 后面我们研究如何破坏…...

强化学习RL 01~ 数学基础
目录 RL理解要点 1. RL数学基础 1.1 Random Variable 随机变量 1.2 概率密度函数 Probability Density Function(PDF) 1.3 期望 Expectation 1.4 随机抽样 Random Sampling 2. RL术语 Terminologies 2.1 agent、state 和 action 2.2 策略 policy π 2.3 奖励 reward …...
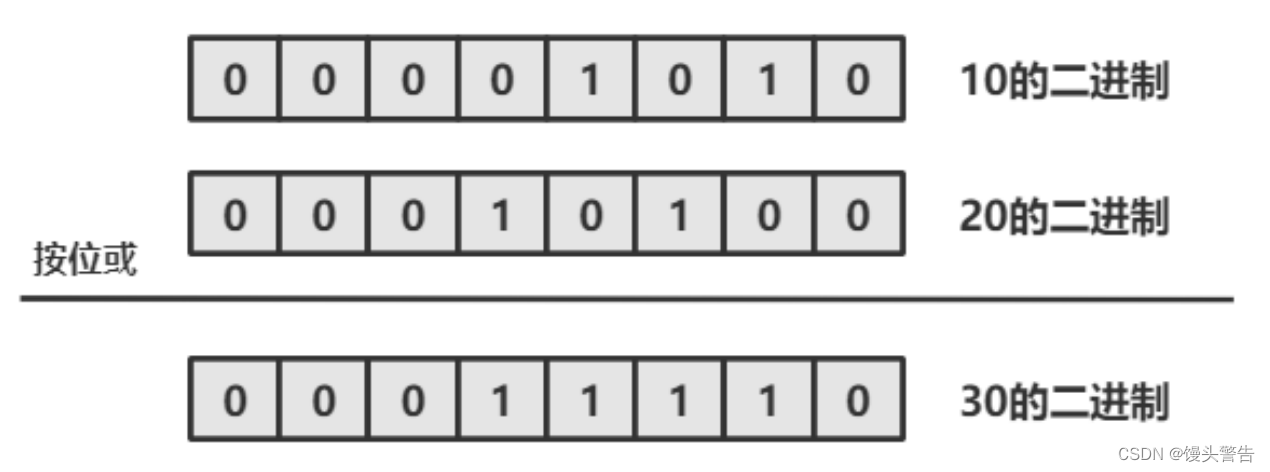
Java的运算符
目录 一、什么是运算符 二、算术运算符 1. 基本四则运算符:加减乘除模( - * / %) 2、增量运算符 - * % 3. 自增/自减运算符 -- 三、关系运算符 四、 逻辑运算符(重点) 1. 逻辑与 && 2. 逻辑或 || 3. 逻辑非 ! 4. 短路求值…...

扫地机器人(蓝桥杯C/C++)
题目描述 小明公司的办公区有一条长长的走廊,由 NN 个方格区域组成,如下图所示。 走廊内部署了 KK 台扫地机器人,其中第 ii 台在第 A_iAi 个方格区域中。已知扫地机器人每分钟可以移动到左右相邻的方格中,并将该区域清扫干净。…...
如何理解API?API 是如何工作的?(5分钟诠释)
大家可能最近经常听到 API 这个概念,那什么是API,它又有什么特点和好处呢? wiki 百科镇楼 …[APIs are] a set of subroutine definitions, protocols, and tools for building application software. In general terms, it’s a set of cle…...

PAT--1111 对称日
央视新闻发了一条微博,指出 2020 年有个罕见的“对称日”,即 2020 年 2 月 2 日,按照 年年年年月月日日 格式组成的字符串 20200202 是完全对称的。 给定任意一个日期,本题就请你写程序判断一下,这是不是一个对称日&a…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...
