2023.10.18 信息学日志
1. CF1689D Lena and Matrix
题目描述
- n ⋅ m n \cdot m n⋅m 的矩阵,求矩阵上任意一点坐标使得到矩阵上的关键点曼哈顿距离最大值最小。
- 数据范围: ∑ n ⋅ m ≤ 1 0 6 \sum n \cdot m \leq 10^6 ∑n⋅m≤106
题目概况
来源:Codeforces
洛谷难度:蓝题
CF难度: 1900 1900 1900
标签:枚举 最短距离
思路点拨
考虑每个点,只需要关注它到其他点曼哈顿距离的最大值,而实际上全局只会有 4 4 4 个点真正会影响最大值。
d i s = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ dis = |x_1-x_2|+|y_1-y_2| dis=∣x1−x2∣+∣y1−y2∣ 将绝对值拆开分为4种情况,如下:
-
d i s = x 1 − x 2 + y 1 − y 2 dis = x_1-x_2+y_1-y_2 dis=x1−x2+y1−y2
-
d i s = x 1 − x 2 + y 2 − y 1 dis = x_1-x_2+y_2-y_1 dis=x1−x2+y2−y1
-
d i s = x 2 − x 1 + y 1 − y 2 dis = x_2-x_1+y_1-y_2 dis=x2−x1+y1−y2
-
d i s = x 2 − x 1 + y 2 − y 1 dis = x_2-x_1+y_2-y_1 dis=x2−x1+y2−y1
设定 ( x 1 , y 1 ) (x_1,y_1) (x1,y1) 为关键点,若使 d i s dis dis 最大,推广一下 ( x 2 , y 2 ) (x_2,y_2) (x2,y2) 作为四至点(地理)需要满足以下 4 4 4 点之一:
-
min ( x 2 + y 2 ) \min(x_2+y_2) min(x2+y2)
-
min ( x 2 − y 2 ) \min(x_2-y_2) min(x2−y2)
-
max ( x 2 − y 2 ) \max(x_2-y_2) max(x2−y2)
-
max ( x 2 + y 2 ) \max(x_2+y_2) max(x2+y2)
先预处理出四至点,再暴力每个点到四至点的曼哈顿距离最大值的最小值(打擂台).
预处理时间复杂度: O ( 4 ⋅ n ) O(4 \cdot n) O(4⋅n)
打擂台时间复杂度: O ( 4 ⋅ n ) O(4 \cdot n) O(4⋅n)
A C AC AC.
题目收获
将关键式分解压缩解空间。
2. CF1380D Berserk And Fireball
题目描述
CF1380D 传送门
题目概况
来源:Codeforces
洛谷难度:蓝题
CF难度: 2000 2000 2000
标签:双指针 ST表 贪心
思路点拨
-
毋庸置疑的是因为每个人的战力不同,所以通过双指针直接判定 a 、 b a、b a、b 数组是否一一对应.不对应直接 − 1 -1 −1.
-
此时 a a a 数组已经被 b b b 数组元素切成了 [ l , r ] [l,r] [l,r] 的区间,只需要考虑这样的区间该如何处理.
-
设 p = r − l + 1 p=r-l+1 p=r−l+1 以下分为 2 2 2 种情况:
- p < k p<k p<k。处理区间内最大值,若最大值大于 2 2 2 端点 b b b 数组数值,则 − 1 -1 −1 ; 否则该区间代价为 p ⋅ y p \cdot y p⋅y (y为狂暴术代价,x为火球术代价)
- k ≤ p k \leq p k≤p
- 火球术代价比狂暴术代价优
⌊ p k ⌋ ⋅ x + p m o d k ⋅ y \lfloor \frac{p}{k}\rfloor \cdot x + p \mod k \cdot y ⌊kp⌋⋅x+pmodk⋅y - 反之
x + ( p − k ) ⋅ y x+(p-k)\cdot y x+(p−k)⋅y
- 火球术代价比狂暴术代价优
-
完善, a a a 数组区间最值用 S T ST ST 表预处理维护
时间复杂度: O ( n ⋅ l o g 2 ( n ) ) O(n \cdot log2(n)) O(n⋅log2(n))
A C AC AC.
题目收获
将题目分区间缩小范围。
3. P2568 GCD
题目描述
P2568 传送门
题目概况
来源:Codeforces
洛谷难度:蓝题
标签:数论 欧拉函数 gcd \gcd gcd 前缀和
思路点拨
题目显而易见,先推一下式子。
- 原始: ∑ p ∈ p r i m e ∑ i = 1 n ∑ j = 1 n [ gcd ( i , j ) = = p ] \sum _{p∈prime}\sum_{i=1}^{n}\sum_{j=1}^{n}[\gcd(i,j)==p] ∑p∈prime∑i=1n∑j=1n[gcd(i,j)==p]
- ①: ∑ p ∈ p r i m e ∑ i = 1 ⌊ n p ⌋ ∑ j = 1 ⌊ n p ⌋ [ gcd ( i , j ) = = 1 ] \sum _{p∈prime}\sum_{i=1}^{\lfloor\frac{n}{p}\rfloor}\sum_{j=1}^{\lfloor\frac{n}{p}\rfloor}[\gcd(i,j)==1] ∑p∈prime∑i=1⌊pn⌋∑j=1⌊pn⌋[gcd(i,j)==1]
- ②: ∑ p ∈ p r i m e ∑ i = 1 ⌊ n p ⌋ ( ( 2 ⋅ ∑ j = 1 i [ gcd ( i . j ) = = 1 ] ) − 1 ) \sum _{p∈prime}\sum_{i=1}^{\lfloor\frac{n}{p}\rfloor}((2 \cdot \sum_{j=1}^{i}[\gcd(i.j)==1])-1) ∑p∈prime∑i=1⌊pn⌋((2⋅∑j=1i[gcd(i.j)==1])−1)
- ③: ∑ p ∈ p r i m e ∑ i = 1 ⌊ n p ⌋ ( ( 2 ⋅ φ ( i ) − 1 ) \sum _{p∈prime}\sum_{i=1}^{\lfloor\frac{n}{p}\rfloor}((2 \cdot\varphi(i) -1) ∑p∈prime∑i=1⌊pn⌋((2⋅φ(i)−1)
- ④: ∑ p ∈ p r i m e 2 ⋅ ( ∑ i = 1 ⌊ n p ⌋ φ ( i ) ) − 1 \sum _{p∈prime}2 \cdot(\sum_{i=1}^{\lfloor\frac{n}{p}\rfloor}\varphi(i))-1 ∑p∈prime2⋅(∑i=1⌊pn⌋φ(i))−1
所以可以使用线性筛预处理 φ \varphi φ 函数, 在预处理 φ \varphi φ 函数的前缀和.
O ( n ) O(n) O(n)时间复杂度求解.
A C AC AC.
相关文章:

2023.10.18 信息学日志
1. CF1689D Lena and Matrix 题目描述 n ⋅ m n \cdot m n⋅m 的矩阵,求矩阵上任意一点坐标使得到矩阵上的关键点曼哈顿距离最大值最小。数据范围: ∑ n ⋅ m ≤ 1 0 6 \sum n \cdot m \leq 10^6 ∑n⋅m≤106 题目概况 来源:Codeforces …...
)
Modbus封装库(Com,tcp,udp一应俱全)
自行封装在用的Modbus通迅库,集成了com,tcp,udp, 做个笔记吧, 以下头文件, #pragma once #include <functional> #include <vector> #include <string> #include <memory> #ifdef LIBMODBUS_EXPORTS #define LIBMODBUS_EXPORT_…...

专访HuggingFace CTO:开源崛起、创业故事和AI民主化丨智源独家
导读 HuggingFace CTO Julien Chaumond认为,在大模型时代,AI民主化至关重要。随着大语言模型和复杂人工智能系统的崛起,持续提升AI技术的可及性有助于确保这些技术的获取和控制不集中在少数强大实体手中。技术民主化促进了机会均等࿰…...
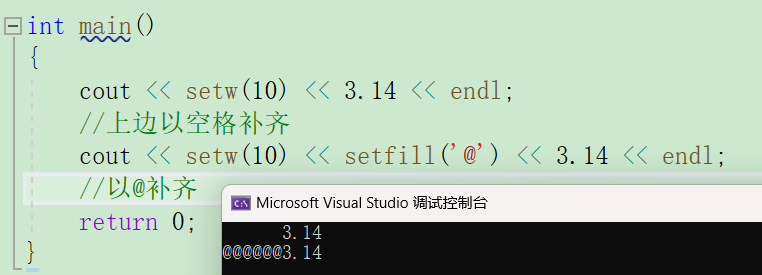
C++常用格式化输出转换
在C语言中可以用printf以一定的格式打印字符,C当然也可以。 输入输出及命名空间还不太了解的小伙伴可以看一看C入门讲解第一篇。 在C中,可以用流操作符(stream manipulators)控制数据的输出格式,这些流操作符定义在2…...

如何使用 Loadgen 来简化 HTTP API 请求的集成测试
引言 在编写 HTTP 服务的过程中,集成测试 1 是保证程序正确性的重要一环,如下图所示,其基本的流程就是不断向服务发起请求然后校验响应的状态和数据等: 为大量的 API 和用例编写测试是一件繁琐的工作,而 Loadgen 2 正…...

软件测试面试大家是不是一问到项目就不会了?
软件测试面试中,介绍做过的项目,可以说是必不可少的一道面试题了,对于面试的同学来说,该自己发挥呢? 把项目的所有功能噼里啪啦说一遍就完事了?当然不是,我们要搞清楚,面试官问这个…...

伐木猪小游戏
欢迎来到程序小院 伐木猪 玩法:控制小猪点击屏幕左右砍树,不能碰到树枝,考验手速与眼力,记录分数,快去挑战伐木吧^^。开始游戏https://www.ormcc.com/play/gameStart/199 html <script type"text/javascript…...
0007Java安卓程序设计-ssm基于Android的校园新闻管理系统
文章目录 **摘** **要**目 录开发环境 编程技术交流、源码分享、模板分享、网课教程 🐧裙:776871563 摘 要 网络的广泛应用给生活带来了十分的便利。所以把校园新闻管理与现在网络相结合,利用java技术建设校园新闻管理系统app,实…...
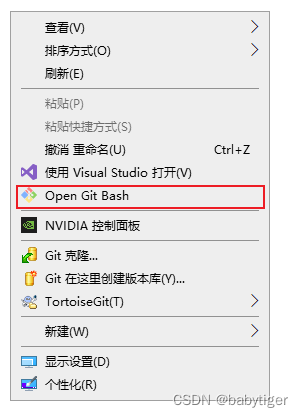
git增加右键菜单
有次不小心清理系统垃圾,把git右击菜单搞没了,下面是恢复方法 将下面代码存为.reg文件,双击后导出生效,注意,你安装的git必须是默认C盘的,如果换了地方要改下面注册表文件中相关的位置 Windows Registry …...

openGauss学习笔记-117 openGauss 数据库管理-设置数据库审计-查看审计结果
文章目录 openGauss学习笔记-117 openGauss 数据库管理-设置数据库审计-查看审计结果117.1 前提条件117.2 背景信息117.3 操作步骤 openGauss学习笔记-117 openGauss 数据库管理-设置数据库审计-查看审计结果 117.1 前提条件 审计功能总开关已开启。需要审计的审计项开关已开…...

学习代码20231106
解释代码:os.environ[“OMP_NUM_THREADS“] “1“ 这行代码涉及到 Python 的 os 模块和环境变量。它的作用是设置名为 “OMPNUMTHREADS” 的环境变量的值为 “1”。让我解释一下各部分的含义: 1.os.environ: 这是 Python 中的一个字典,包含…...

turtle绘制分形树-第10届蓝桥杯省赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第5讲。 turtle绘制分形树&…...

【大厂招聘试题】__硬件工程师_2021年“美团”校招
目录 匹配职位:硬件工程师 1.(多选题)单处理系统中,进程P1,P2,P3处于就绪队列,进程P4,P6处于等待队列,P5正占用处理器运行,以下对接下来的运行合理的分析是( ÿ…...

算法通关村第七关|黄金挑战|迭代实现二叉树的前、中、后序遍历
1.迭代实现前序遍历 public List<Integer> preOrderTraversal(TreeNode root) {List<Integer> res new ArrayList<Integer>();if (root null) {return res;}Deque<TreeNode> stack new LinkedList<TreeNode>();TreeNode node root;while (!…...

了解高防服务器的工作原理
在当今互联网时代,网络安全问题日益突出,各种网络攻击层出不穷。为了保护企业的网络安全,高防服务器应运而生。那么,你是否了解高防服务器的工作原理呢?下面就让我们一起来探索一下。 高防服务器是一种能够有效抵御各种网络攻击的…...

AVL树性质和实现
AVL树 AVL是两名俄罗斯数学家的名字,以此纪念 与二叉搜索树的区别 AVL树在二叉搜索树的基础上增加了新的限制:需要时刻保证每个树中每个结点的左右子树高度之差的绝对值不超过1 因此,当向树中插入新结点后,即可降低树的高度&…...

出口贸易媒体发稿推广6个技巧提升品牌知名度-华媒舍
1. 出口贸易媒体介绍 出口贸易媒体是指专注于报道国际贸易、跨境业务和进出口市场的媒体平台。这些媒体对于企业发展来说至关重要,可以帮助品牌扩大影响力、提升知名度,促进商业合作。下面介绍6个出口贸易媒体发稿推广技巧,帮助企业更好地利…...
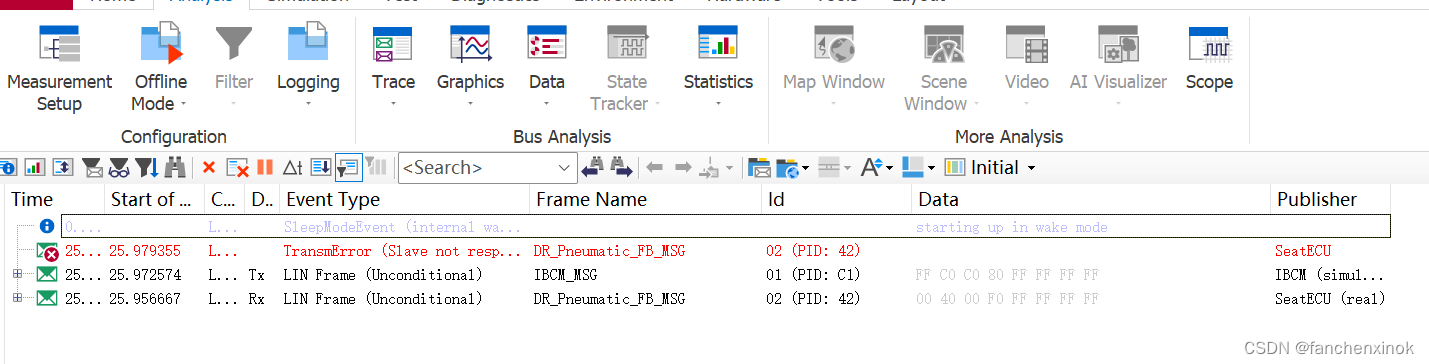
学习笔记:CANOE模拟LIN主节点和实际从节点进行通信测试
先写点感想,在LIN开发阶段,我一般用图莫斯USB工具来进行模拟主机节点发送数据。后来公司买了CANOE工具就边学习边搭建了LIN的测试工程,网上的资料真的很少,主要是靠自己一点点摸索前进,总算入门。几个月后的今天&#…...
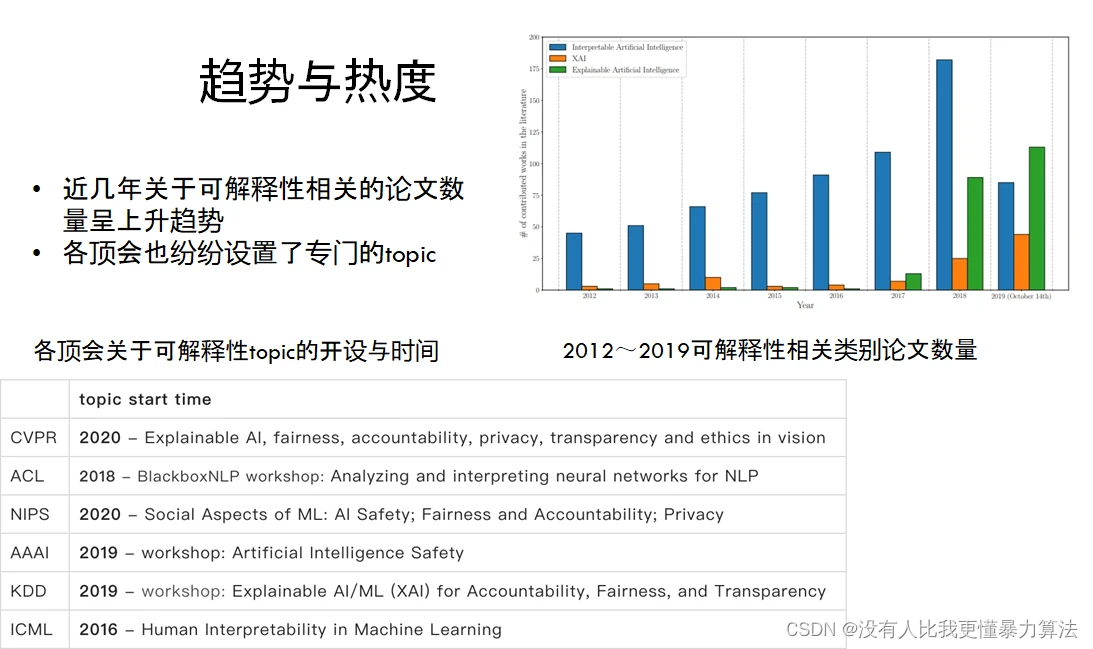
模型可解释性
模型可解释性 前言导读Background1、为什么需要可解释性?2、诞生背景3、研究现状4、常见的模型可解释性方法4.1 基于模型自身的可解释性1)Explanation Generation2)Prototype Network 4.2 基于结果的可解释性 5、应用前景6、面临挑战 前言导读…...

Django初窥门径-自定义用户模型
前言 自定义用户模型在Django应用中是一个重要的话题,它涉及到如何根据您的项目需求以及特定的用户身份验证和授权需求来调整用户模型。在以下前言中,我将讲述为什么自定义用户模型是如此重要以及其潜在的优势: 随着Web应用的不断发展&…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

基于Python的气象数据分析及可视化研究
目录 一.🦁前言二.🦁开源代码与组件使用情况说明三.🦁核心功能1. ✅算法设计2. ✅PyEcharts库3. ✅Flask框架4. ✅爬虫5. ✅部署项目 四.🦁演示效果1. 管理员模块1.1 用户管理 2. 用户模块2.1 登录系统2.2 查看实时数据2.3 查看天…...

[QMT量化交易小白入门]-六十二、ETF轮动中简单的评分算法如何获取历史年化收益32.7%
本专栏主要是介绍QMT的基础用法,常见函数,写策略的方法,也会分享一些量化交易的思路,大概会写100篇左右。 QMT的相关资料较少,在使用过程中不断的摸索,遇到了一些问题,记录下来和大家一起沟通,共同进步。 文章目录 相关阅读1. 策略概述2. 趋势评分模块3 代码解析4 木头…...
