NOIP2023模拟13联测34 competition
题目大意
有一场题目数量为 m m m的比赛,有一个团队想要来参加。
这个团队有 n n n个选手,编号为 i i i的选手能做第 l i ∼ r i l_i \sim r_i li∼ri道题,每题他都有 100 % 100\% 100%的概率做出来。
这个团队会随机派出一只队伍来参加这个比赛。
因为编号相邻的人关系更好,默契度也更高,所以一个团队派出的队伍一直都是编号为连续区间的选手。
一个队伍的得分为该队伍能做出的题的数量,求这个团队参加比赛的期望得分。输出答案模 1 0 9 + 7 10^9+7 109+7后的值。
注: 一道题只能被做出来一次。
1 ≤ n ≤ 1 0 6 , 1 ≤ l i ≤ r i ≤ m ≤ 1 0 18 1\leq n\leq 10^6,1\leq l_i\leq r_i\leq m\leq 10^{18} 1≤n≤106,1≤li≤ri≤m≤1018
时间限制 2000 m s 2000ms 2000ms,空间限制 512 M B 512MB 512MB。
题解
直接求能做出多少道题并不简单,我们换一种思路:对于每道题,有多少种队伍做不出这道题?
对于每道题 k k k,我们设 z i z_i zi表示 k k k是否包含在 [ l i , r i ] [l_i,r_i] [li,ri]中,也就是第 i i i个人能不能做出这道题。那么,如果当前的队伍不能做出这道题,那选择的区间就不能包含任意一个 z i = 1 z_i=1 zi=1的 i i i。也就是说,将所有 z i = 1 z_i=1 zi=1的 i i i放在一起,则相邻的两个数 i , j i,j i,j之间有 t = j − i − 1 t=j-i-1 t=j−i−1个人不会做这道题,那么这部分中有 t ( t + 1 ) 2 \dfrac{t(t+1)}{2} 2t(t+1)种队伍的选法使得这道题不能被做出来。
我们先求每种方案的得分之和,那么可以先将每种方案的得分都先看作 m m m,然后再减去不能做出的题目。
对于每道题 k k k,维护在 i i i之前最后一个能做出这道题的人 l s t k lst_k lstk。然后遍历每个人,遍历 l i l_i li到 r i r_i ri,每个位置 k k k的贡献为 t ( t + 1 ) 2 \dfrac{t(t+1)}{2} 2t(t+1),其中 t = i − l s t k − 1 t=i-lst_k-1 t=i−lstk−1,然后令 l s t k = i lst_k=i lstk=i。这样做的话,时间复杂度为 O ( n m ) O(nm) O(nm)。下面考虑优化。
我们用一个 v e c t o r vector vector来存储 l s t lst lst值相同的每一个区间,一开始总共只有一个区间 [ 1 , m ] [1,m] [1,m], l s t lst lst值都是 0 0 0。对于每个人 i i i,都要修改 [ l i , r i ] [l_i,r_i] [li,ri]上的 l s t lst lst值。那么,我们对于 v e c t o r vector vector中每一个与 [ l i , r i ] [l_i,r_i] [li,ri]有交集的区间 [ a , b ] [a,b] [a,b],将这些区间与 [ l i , r i ] [l_i,r_i] [li,ri]有交集的部分按上面的方法向答案做出 t ( t + 1 ) 2 × ( b − a + 1 ) \dfrac{t(t+1)}{2}\times (b-a+1) 2t(t+1)×(b−a+1)的贡献(注意这里的贡献是负的,是在原本将这道题看作做对,然后在减去不能做对的方案数乘上题目数量),因为这个区间表示 m m m道题中的 b − a + 1 b-a+1 b−a+1道题,所以要乘上 ( b − a + 1 ) (b-a+1) (b−a+1)。再把有交集部分删掉,没有交集的部分再放回去。最后加上一个区间 [ l i , r i ] [l_i,r_i] [li,ri], l s t lst lst值为 i i i。因为最后还有一部分没有算贡献的,我们可以在最后再加入一个区间 [ 1 , m ] [1,m] [1,m], l s t lst lst值为 n + 1 n+1 n+1,就能够统计到这部分的贡献。
这样做的话会不会 TLE \text{TLE} TLE呢?不会。因为每次加入一个区间最多能够产生 3 3 3个区间(这个区间本身,与这个区间有交集的区间中最左边的没有交集的部分,与这个区间有交集的区间中最右边的没有交集的部分),为保证区间是从小到大排序的,所以加入一次区间的时间复杂度为 O ( log n ) O(\log n) O(logn)(区间总数不会超过 3 n 3n 3n)。而每个区间在之后如果与新加入的区间有交集,则这个区间就会被删去,也就是说在之后最多只造成 O ( 1 ) O(1) O(1)的时间复杂度。所以,总时间复杂度为 O ( n log n ) O(n\log n) O(nlogn)。
我们最终得到了每种方案的得分之和,再乘上方案数的逆元即可。
时间复杂度为 O ( n log n ) O(n\log n) O(nlogn)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1000000;
const long long mod=1e9+7;
int n;
long long m,ans=0;
struct node{long long x,y,w;bool operator<(const node ax)const{return y<ax.y;}
};
vector<node>v;
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
long long gt(long long k){return k*(k+1)/2%mod;
}
void pt(long long x,long long y,long long w){auto it=lower_bound(v.begin(),v.end(),(node){0,x,0});node vl=(node){0,0,-1},vr=(node){0,0,-1};while((*it).x<=y){if((*it).x<x) vl=(node){(*it).x,x-1,(*it).w};if((*it).y>y) vr=(node){y+1,(*it).y,(*it).w};long long vx=max(x,(*it).x),vy=min(y,(*it).y);ans=(ans-(vy-vx+1)%mod*gt(w-(*it).w-1)%mod+mod)%mod;v.erase(it);}int vt=it-v.begin();if(vr.w!=-1) v.insert(v.begin()+vt,vr);v.insert(v.begin()+vt,(node){x,y,w});if(vl.w!=-1) v.insert(v.begin()+vt,vl);
}
int main()
{
// freopen("competition.in","r",stdin);
// freopen("competition.out","w",stdout);scanf("%d%lld",&n,&m);ans=m%mod*gt(n)%mod;v.push_back((node){1,m,0});v.push_back((node){m+1,m+1,0});for(int i=1;i<=n;i++){long long x,y;scanf("%lld%lld",&x,&y);pt(x,y,i);}pt(1,m,n+1);ans=ans*mi(gt(n),mod-2)%mod;printf("%lld",ans);return 0;
}
相关文章:

NOIP2023模拟13联测34 competition
题目大意 有一场题目数量为 m m m的比赛,有一个团队想要来参加。 这个团队有 n n n个选手,编号为 i i i的选手能做第 l i ∼ r i l_i \sim r_i li∼ri道题,每题他都有 100 % 100\% 100%的概率做出来。 这个团队会随机派出一只队伍来参…...
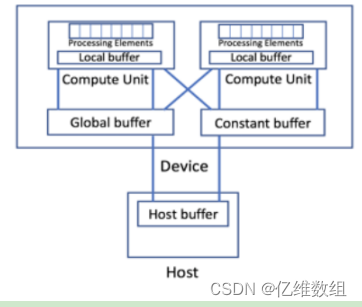
Intel oneAPI笔记(2)--jupyter官方文档(oneAPI_Intro)学习笔记
前言 本文是对jupyterlab中oneAPI_Essentials/01_oneAPI_Intro文档的学习记录,包含对SYCL、DPC extends SYCL、oneAPI Programming models等介绍和SYCL代码的初步演示等内容 oneAPI编程模型综述 oneAPI编程模型提供了一个全面而统一的开发人员工具组合࿰…...
用 QT 开发软件会吃官司吗?
之前我写过我们现在使用 QT 开发跨平台软件,有朋友留言,QT 虽好,当心收到律师函。今天就来聊聊这个话题。 在开始这个话题之前,我们先把使用盗版 QT 排除在外,只讨论在合法且遵从版权协议的前提下,能否使用…...

远程运维用什么软件?可以保障更安全?
远程运维顾名思义就是通过远程的方式IT设备等运行、维护。远程运维适用场景包含因疫情居家办公,包含放假期间出现运维故障远程解决,包含项目太远需要远程操作等等。但远程运维过程存在一定风险,安全性无法保障,所以一定要选择靠谱…...

数据结构与算法C语言版学习笔记(2)-线性表、顺序存储结构的线性表
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 数据结构部分的知识框架一、线性表的定义和特点1.定义2.特点 二、线性表的实际案例引入1.案例一:多项式的加减乘除2.案例二:当多项式是稀疏多…...
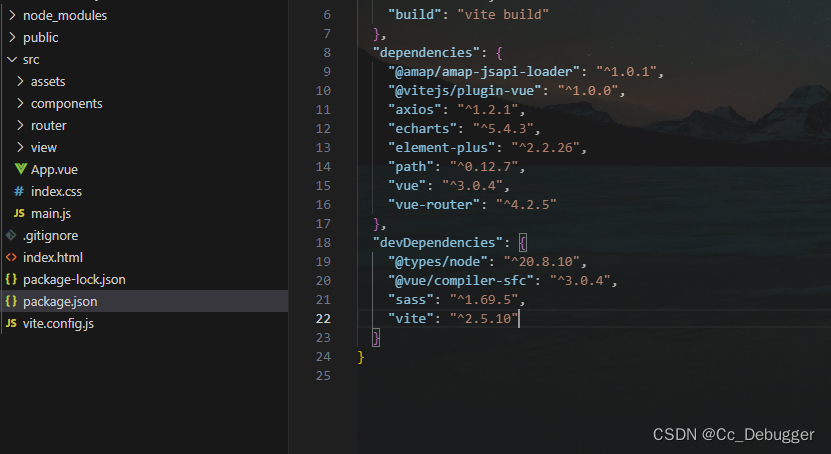
【vite】vite.defineConfig is not a function/npm无法安装第三方包问题
当使用vite命令 npm init vite-app 项目名称时配置 import vue from vitejs/plugin-vueexport default defineConfig({plugins: [vue()] })会报错vite.defineConfig is not a function 还有就是npm下载的时候也会报错 原因vite插件vitejs/plugin-vue和vite版本问题 解决 调…...

234. 回文链表 --力扣 --JAVA
题目 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。 解题思路 判断链表是否为回文链表取决于链表中各个节点的值,所以可以通过存储各节点的值进行对比判断&…...
【JAVA学习笔记】65 - 文件类,IO流--节点流、处理流、对象流、转换流、打印流
项目代码 https://github.com/yinhai1114/Java_Learning_Code/tree/main/IDEA_Chapter19/src/com/yinhai 文件 一、文件,流 文件,对我们并不陌生,文件是保存数据的地方,比如大家经常使用的word文档,txt文件,excel文件..都是文件。它既可以保存一张图片…...

R语言 复习 习题图片
这是日天土申哥不知道从哪淘来的R语言复习知识点图片,大部分内容都是课后习题的答案 加油吧,骚年,考个好分数...
c语言 结构体 简单实例
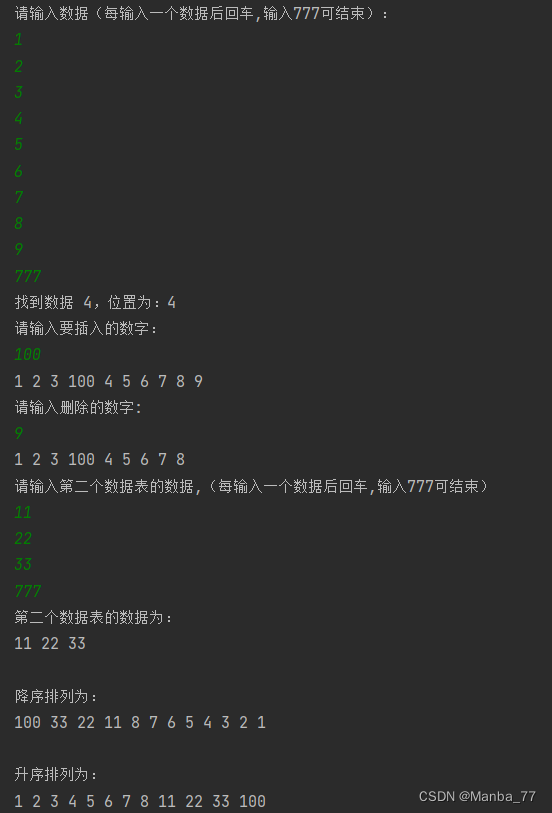
结构体 简单例子 要求: 结构体保存学生信息操作 代码 #include <stdio.h>//定义结构体 struct student{int ID;char name[20];char sex;char birthday[8];int grade; };int main(){int number;printf("请输入学生个数:");scanf(&quo…...

【ChatGPT】ChatGPT的自定义指令
ChatGPT的自定义指令 关于ChatGPT自定义指令的常见问题解答概述可用性如何使用您的数据自定义指令设置将应用于所有新聊天。启动新聊天可查看更改iOS & AndroidWeb 示例常见问题使用自定义指令的好处字符限制我的ChatGPT数据导出中是否包含自定义指令?当我删除我…...

《哥德尔、艾舍尔、巴赫——集异璧之大成》阅读笔记1
1、谁也不知道非智能行为和智能行为之间的界限在哪里。事实上,认为存在明显界限也许是愚蠢的。但是智能的基本能力还是确定的,它们是: 对于情境有很灵活的反应充分利用机遇弄懂含糊不清或彼此矛盾的信息认识到一个情境中什么是重要的因素&am…...

稳定细胞系构建技术介绍
抗体药物的开发是一个非常复杂的过程,构建适用于工业生产的高表达的稳定细胞株是抗体药工艺开发的起点和基础。一株稳定高产的工程细胞株不仅能显著增加单位体积产量,降低生产成本,还可以降低下游纯化工艺复杂度,确保获得安全&…...
k8s部署srs服务
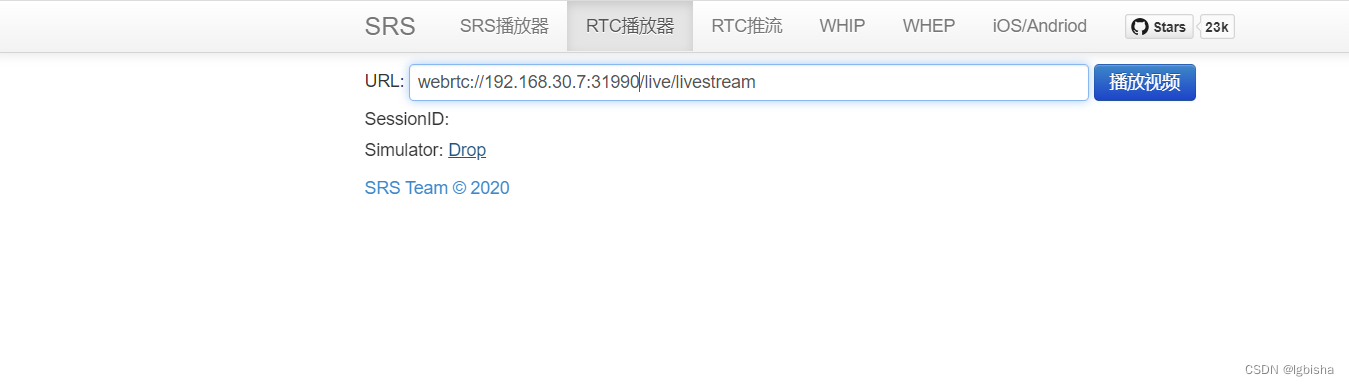
k8s部署srs服务 项目需要把srs纳入k8s进行管理,需要通过k8s来部署srs服务然后原本的srs可以支持rtmp与webrtc两种,官网查了部署方式,k8s只有最基本的部署方式于是开始研究k8s部署能够正常推拉流的webrtc版本的srs 首先肯定是去官网查有无相关…...

使用Java分割PDF文件
在Java中,我们可以使用iText库来处理PDF文件。iText是一个流行的Java库,用于创建和处理PDF文件。在本篇博客中,我们将介绍如何使用Java分割一个PDF文件为多个小的PDF文件。 1. 引入iText依赖 首先,我们需要在项目中引入iText库的…...

LLM时代中的分布式AI
深度学习相较传统机器学习模型,对算力有更高的要求。尤其是随着深度学习的飞速发展,模型体量也不断增长。于是,前几年,我们看到了芯片行业的百家争鸣和性能指标的快速提升。正当大家觉得算力问题已经得到较大程度的缓解时…...
Zinx框架-游戏服务器开发003:架构搭建-需求分析及TCP通信方式的实现
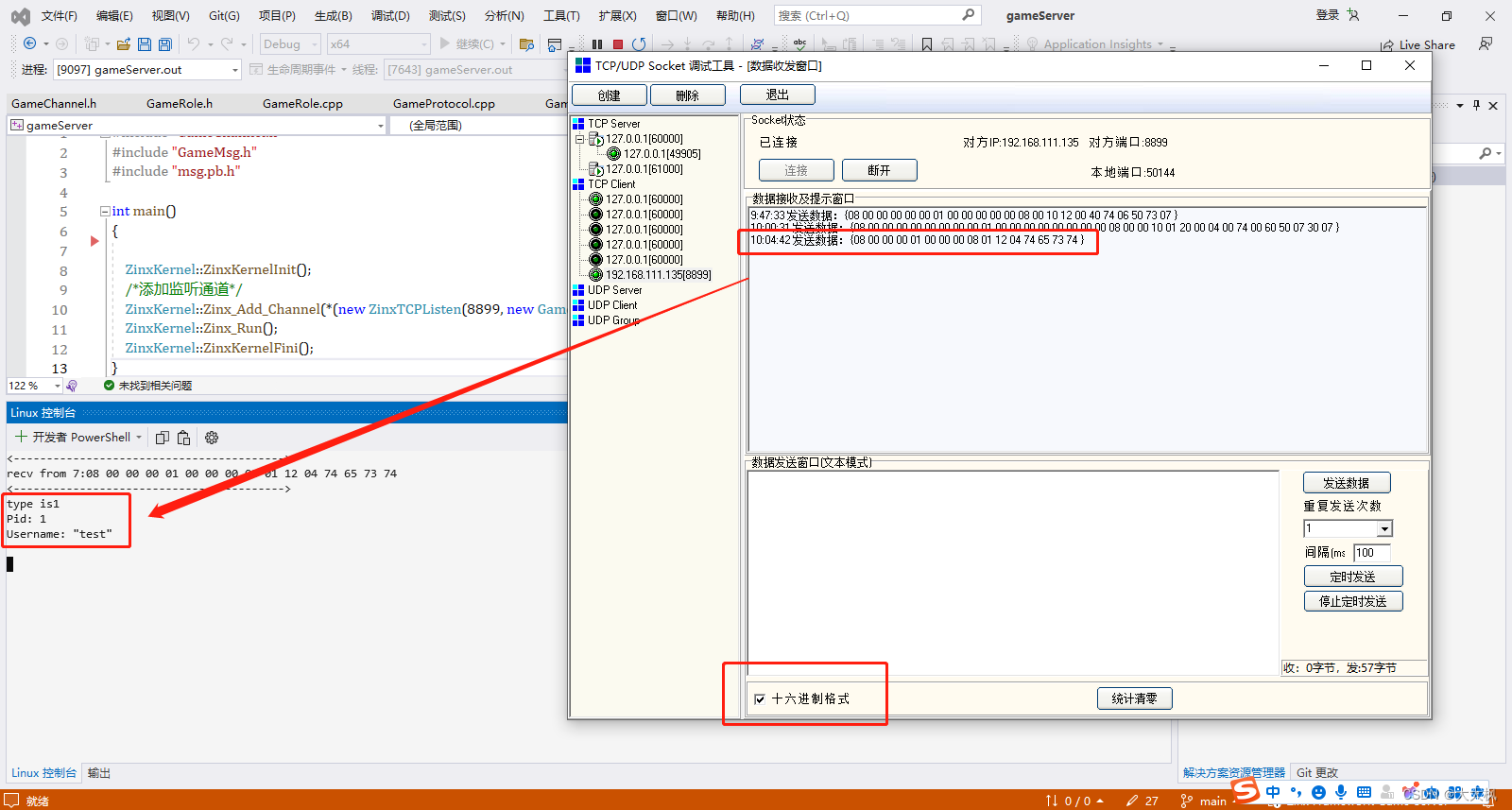
文章目录 1 项目总体架构2 项目需求2.1 服务器职责2.2 消息的格式和定义 3 基于Tcp连接的通信方式3.1 通道层实现GameChannel类3.1.1 TcpChannel类3.1.2 Tcp工厂类3.1.3 创建主函数,添加Tcp的监听套接字3.1.4 代码测试 3.2 协议层与消息类3.2.1 消息的定义3.2.2 消息…...

如何使用Pyarmor保护你的Python脚本
目录 一、Pyarmor简介 二、使用Pyarmor保护Python脚本 1、安装Pyarmor 2、创建Pyarmor项目 3、添加Python脚本 4、配置执行环境 5、生成保护后的脚本 三、注意事项与未来发展 四、未来发展 五、总结 本文深入探讨了如何使用Pyarmor工具保护Python脚本。Pyarmor是一个…...

【c++】搜索二叉树的模拟实现
搜索二叉树的模拟实现 k模型完整代码 #pragma once namespace hqj1 {template<class K>struct SBTreeNode{public://这里直接用匿名对象作为缺省参数SBTreeNode(const K& key K()):_key(key), _cleft(nullptr), _cright(nullptr){}public:K _key;SBTreeNode* _cle…...
)
Kubeadm - K8S1.20 - 高可用集群部署(博客)
这里写目录标题 Kubeadm - K8S1.20 - 高可用集群部署一.环境准备1.系统设置 二.所有节点安装docker三.所有节点安装kubeadm,kubelet和kubectl1.定义kubernetes源2.高可用组件安装、配置 四.部署K8S集群五.问题解决1.加入集群的 Token 过期2.master节点 无法部署非系…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
