NOIP2023模拟13联测34 总结
NOIP2023模拟13联测34 总结
文章目录
- NOIP2023模拟13联测34 总结
- 比赛过程
- 题目
- A. origen
- 题目大意
- 思路
- B.competition
- 题目大意
- 思路
- C. tour
- 题目大意
- D.abstract
- 题目大意
比赛过程
看了一下题,感觉就 T 2 T2 T2 有一点思路。
T 1 T1 T1 先打一个 30 30 30 分暴力,感觉要分位考虑,想了大概 1 h 1h 1h 就跳了。
T 2 T2 T2 想到了先求出整个区间的长度乘上包含这个区间的总数再减去重复算的,想了很久,只会相邻的,只好打个暴力,发现线段树超时,加上离散化又挂了,于是调了好久都没调出来。只好跳了
T 3 T3 T3 赶紧打个暴力
T 4 T4 T4 检查了前 3 3 3 题代码后没什么时间了,题也没看懂
题目
A. origen
题目大意
给定 n n n 个整数 a 1 , a 2 , a 3 ⋯ a n a_1,a_2,a_3\cdots a_n a1,a2,a3⋯an ,求
∑ i = 1 n ∑ j = i n ( ⊕ k = i j a k ) 2 m o d 998244353 \sum_{i = 1}^n\sum_{j = i}^n(\oplus_{k = i}^ja_k)^2 \mod 998244353 i=1∑nj=i∑n(⊕k=ijak)2mod998244353
n ≤ 2 ∗ 1 0 5 , 0 ≤ a i ≤ 2 ∗ 1 0 5 n\le 2 * 10^5 , 0\le a_i \le 2 * 10 ^5 n≤2∗105,0≤ai≤2∗105
思路
设 s i = ⊕ j = 1 i a j s_i = \oplus_{j = 1}^i a_j si=⊕j=1iaj ,则原式变为:
∑ i = 0 n − 1 ∑ j = 1 n ( s i ⊕ s j ) 2 \sum_{i = 0}^{n - 1} \sum_{j = 1}^n (s_i \oplus s_j)^2 i=0∑n−1j=1∑n(si⊕sj)2
按位考虑,一个数可以用二次幂的和来表示。考虑怎么处理平方。
因为:
( ∑ i = 1 n a i ) 2 = ∑ i = 1 i a i 2 + 2 ∑ i = 1 n − 1 ∑ j = i + 1 n a i ∗ a j (\sum_{i = 1}^n a_i)^2 = \sum_{i = 1}^i a_i^2+ 2\sum_{i = 1}^{n - 1}\sum_{j = i +1}^n a_i*a_j (i=1∑nai)2=i=1∑iai2+2i=1∑n−1j=i+1∑nai∗aj
把两部分分开处理。
先处理前面的那项
把 i i i 的每一位分开求贡献,当前处理到第 j j j 位
设前 i − 1 i - 1 i−1 个数这一位为 0 0 0 的数有 s 0 s0 s0 个,为 1 1 1 的数有 s 1 s1 s1 个
那么求这一位的贡献
- 若当前这一位为 1 1 1 : 2 j ∗ 2 ∗ s 0 2^j*2*s0 2j∗2∗s0
- 若当前这一位为 0 0 0 : 2 j ∗ 2 ∗ s 1 2^j*2*s1 2j∗2∗s1
然后处理后面的那项
先枚举两位 j 1 , j 2 j1 , j2 j1,j2
当前处理到第 i i i 位
设 s u m k , l sum_{k , l} sumk,l 为前面 i − 1 i - 1 i−1 个数的第 j 1 j1 j1 位为 k k k ,第 j 2 j2 j2 位为 l l l 的个数
设第 i i i 个数这两位分别是 x , y x , y x,y
那么这里的贡献为: 2 ∗ 2 j 1 ∗ 2 j 2 ∗ s u m ! x , ! y 2 *2^{j1} * 2^{j2} *sum_{!x , !y} 2∗2j1∗2j2∗sum!x,!y
B.competition
题目大意
现在有 n n n 个区间 [ l i , r i ] [l_i , r_i] [li,ri] ,现在问你选取若干的连续的区间的区间并的大小的和。
思路
设 p r e i , j pre_{i , j} prei,j 表示前 i − 1 i - 1 i−1 个区间内,包含点 j j j 的最靠右的数是多少。
可以发现答案就是
∑ i = 1 n ( r i − l i + 1 ) ∗ i ∗ ( n − i + 1 ) − p r e i , j ∗ ( n − i + 1 ) \sum_{i = 1}^n (r_i - l_i +1) * i * (n - i + 1) - pre_{i , j} * (n - i +1) i=1∑n(ri−li+1)∗i∗(n−i+1)−prei,j∗(n−i+1)
也就是这个区间被记入答案的次数乘上区间的大小再减去重复的次数
可以用一棵线段树维护加离散化来维护。
先统计答案,然后用线段树更新 p r e pre pre
要卡常
C. tour
题目大意
有 n n n 个城市,每个城市有一个文化值 v a l i val_i vali
接下来有两种操作
-
0 x y
表示城市 x x x 和城市 y y y 之间建立一条无向边 (保证修建前 x x x 和 y y y 不连通)
-
1 x y
代表有一个人,初始时他的文化值为 0 0 0 ,他会从 x x x 走到 y y y (保证此时 x x x 与 y y y 连通),每走到一个城 市 i i i,他会与这个城市进行文化交流,如果此时他的文化值大于等于 v a l i val_i vali ,那么这次文化交流是 成功的。无论文化交流结果如何,在此之后,他的文化值会加上 v a l i val_i vali 。求出成功的文化交流的次数。
D.abstract
题目大意
定义函数 f ( i , j ) , g ( i , j ) f(i , j) , g(i , j) f(i,j),g(i,j) ,分别表示 i → j i\to j i→j 的权值和权值或,想要求出 ∑ i = 1 n ∑ j = 1 n f ( i , j ) g ( i , j ) \sum_{i = 1}^n\sum_{j = 1}^n f(i , j) ^{g(i , j)} ∑i=1n∑j=1nf(i,j)g(i,j)
把 $f(i , j) , g(i , j) $ 放到 i → j i\to j i→j 的简单路径上的点权和点权或
输出答案 m o d 111121 \mod 111121 mod111121
定义: 0 0 = 0 0^0 = 0 00=0
相关文章:

NOIP2023模拟13联测34 总结
NOIP2023模拟13联测34 总结 文章目录 NOIP2023模拟13联测34 总结比赛过程题目A. origen题目大意思路 B.competition题目大意思路 C. tour题目大意 D.abstract题目大意 比赛过程 看了一下题,感觉就 T 2 T2 T2 有一点思路。 T 1 T1 T1 先打一个 30 30 30 分暴力&am…...

Python武器库开发-常用模块之subprocess模块(十九)
常用模块之subprocess模块(十九) subprocess模块介绍 subprocess 模块允许我们启动一个新进程,并连接到它们的输入/输出/错误管道,从而获取返回值。subprocess 它可以用来调用第三方工具(例如:exe、另一个python文件、命令行工具…...

java验证 Map 的 key、value 是否可以为空
1、验证示例代码 Map<String, Object> maps new HashMap<>();maps.put("a", "1");maps.put(null, null);maps.put("c", null);System.out.println("maps " maps);Object o maps.get(null);System.out.println("o…...

编写MBR主引导记录
BIOS 检测,初始化硬件。挑一些重要的,能保证计算机能运行那些硬件的基本IO操作。 唤醒BIOS 唤醒BIOS需要知道其入口地址,在最后将跳转到0x7c00处 接电的一瞬间,cs:ip寄存器被初始化为0xF000:0xFFF0,所以等效地址是0…...

从零开始搭建React+TypeScript+webpack开发环境-自定义配置化的模拟服务器
技术栈 我们将使用Node.js和Express.js作为我们的后端框架,以及Node.js的文件系统(fs)模块来操作文件和文件夹。此外,我们将使用Node.js的require和delete require.cache来加载和更新模拟数据。 项目结构 首先,让我们定义一个简单的项目结…...

python 之字典的相关知识
文章目录 字典的基本特点:1. 定义2. 键唯一性3. 可变性4. 键的类型 基本操作:字典的创建1. 花括号 {}2. dict() 构造函数3. 键值对的 dict() 构造函数使用 zip() 函数创建字典:注意事项访问字典中的值修改和添加键值对删除键值对 字典方法&am…...

上下游系统对接的沟通与协作
在工作中,有时会有对接其他部门系统的需求,这种需求虽然不复杂,但是跨部门协作,往往会出现各种难以沟通、协调的情况。 踩的坑多了,就记录下来。 注意:在本文中,A系统调用B系统,A依…...
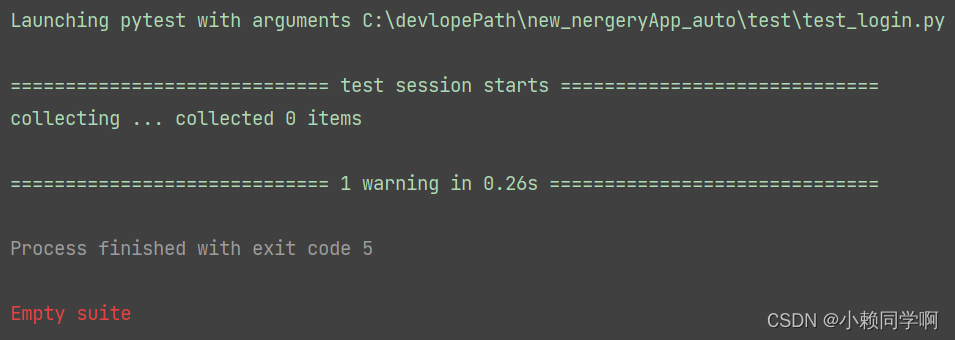
pytest 的使用===谨记
发现用例的规则 a) 文件test_.py开头和_test.py结尾 b) Test开头的类中test开头的方法(测试类不能带有__init__方法) c) 模块中test开头的函数(可以不在class中) 注意点: pytest是以方法为单位发现用例的,你…...
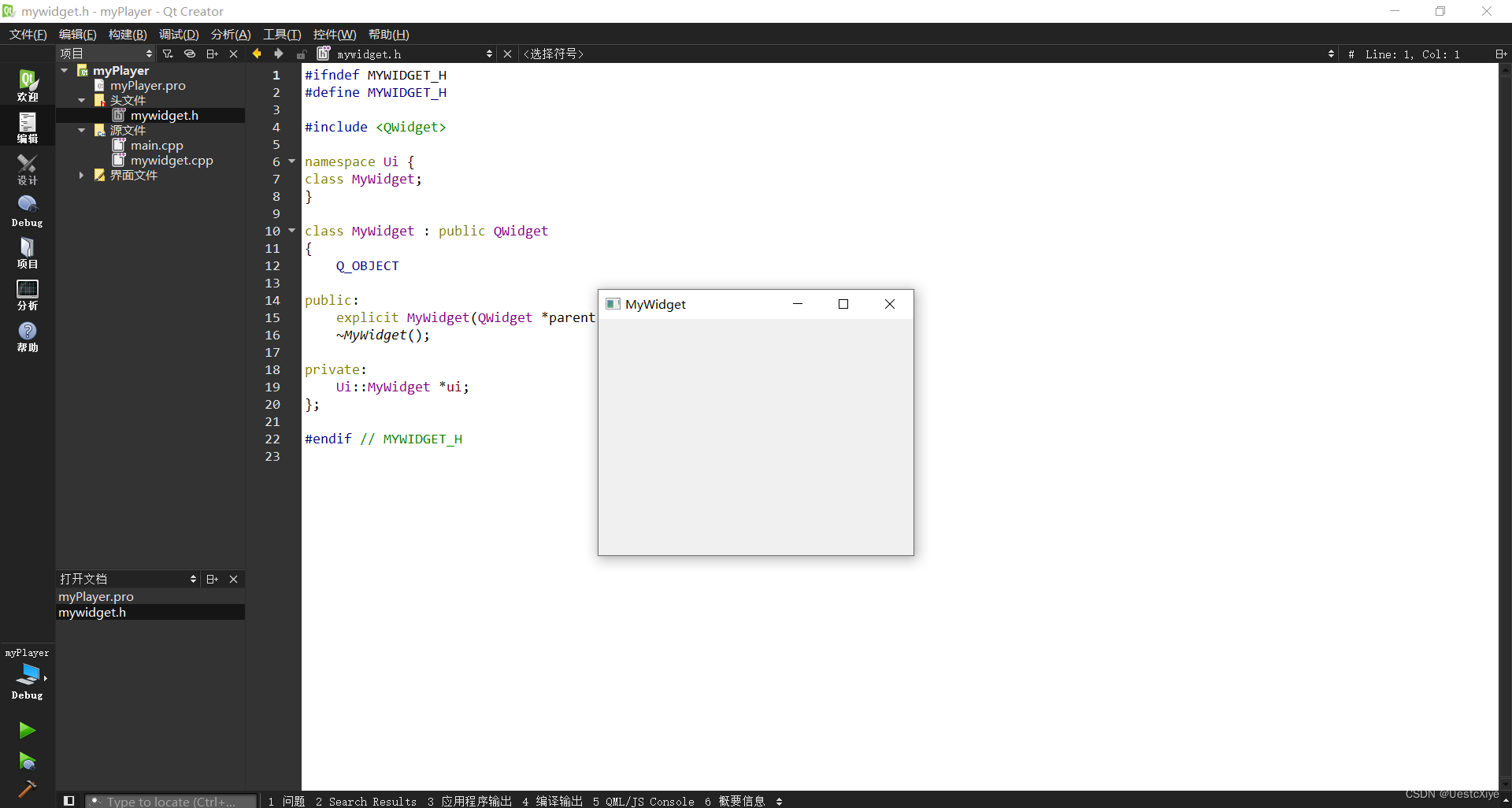
Qt 4.8.6 的下载与安装
Qt 4.8.6 的下载与安装 Qt 4.8.6 的下载与安装下载并解压 MinGW 4.8.2Qt4.8.6 库的安装Qt Creator 3.3.0 的安装配置 Qt Creator测试 官方博客:https://www.yafeilinux.com/ Qt开源社区:https://www.qter.org/ Qt 4.8.6 的下载与安装 学习《Qt Creato…...

图形推理 | 判断推理
文章目录 一、位置规律二、样式规律三、属性规律四、数量规律 一、位置规律 平移 方向:直线(上下、左右、斜对角线)、绕圈(顺逆时针)常见步数:恒定、递增(等差) 旋转 方向ÿ…...
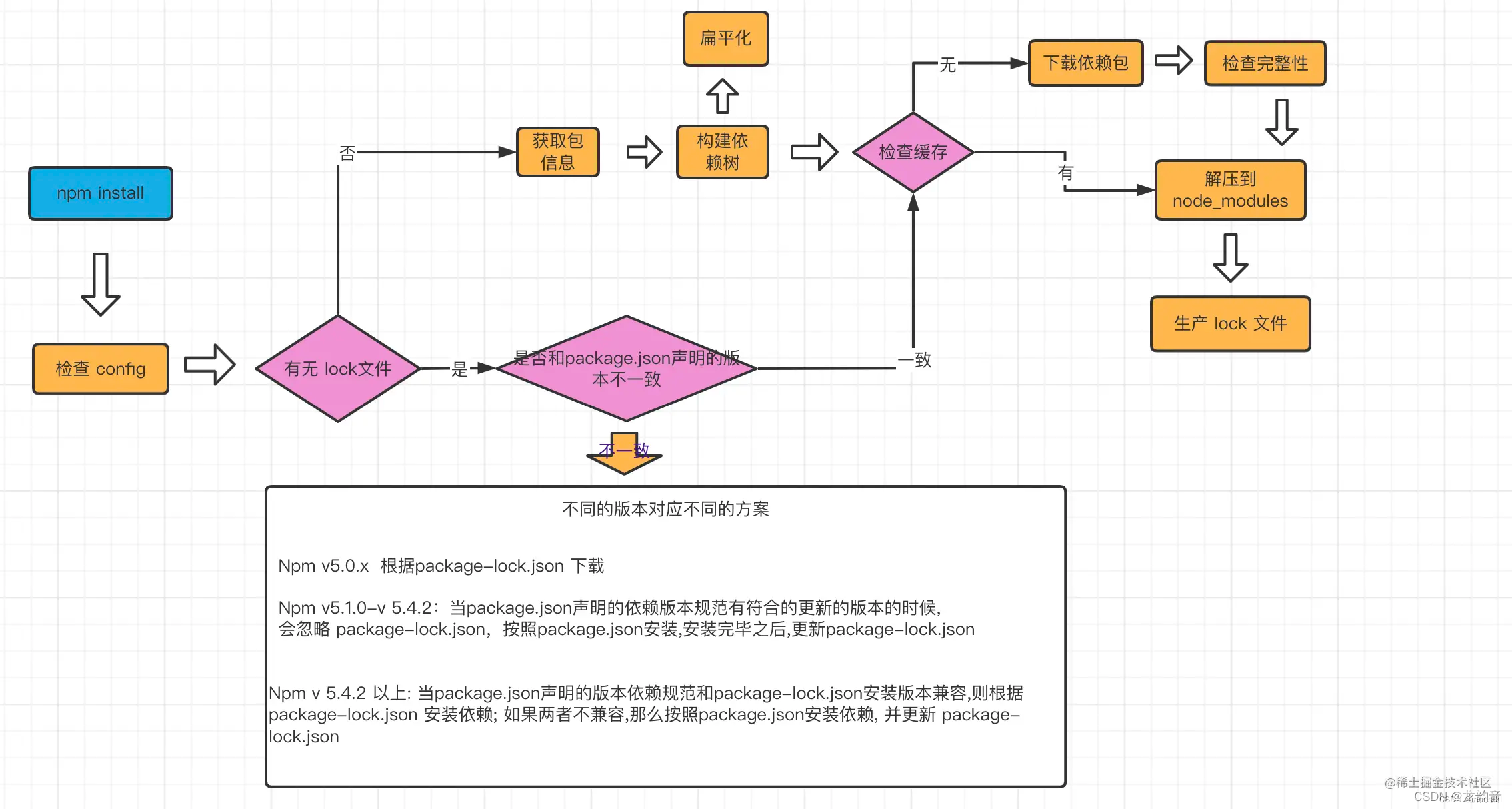
npm的使用
package.json 快速生成package.json npm init -y “version”: “~1.1.0” 格式为:「主版本号. 次版本号. 修订号」。 修改主版本号是做了大的功能性的改动 修改次版本号是新增了新功能 修改修订号就是修复了一些bug dependencies "dependencies": {&…...
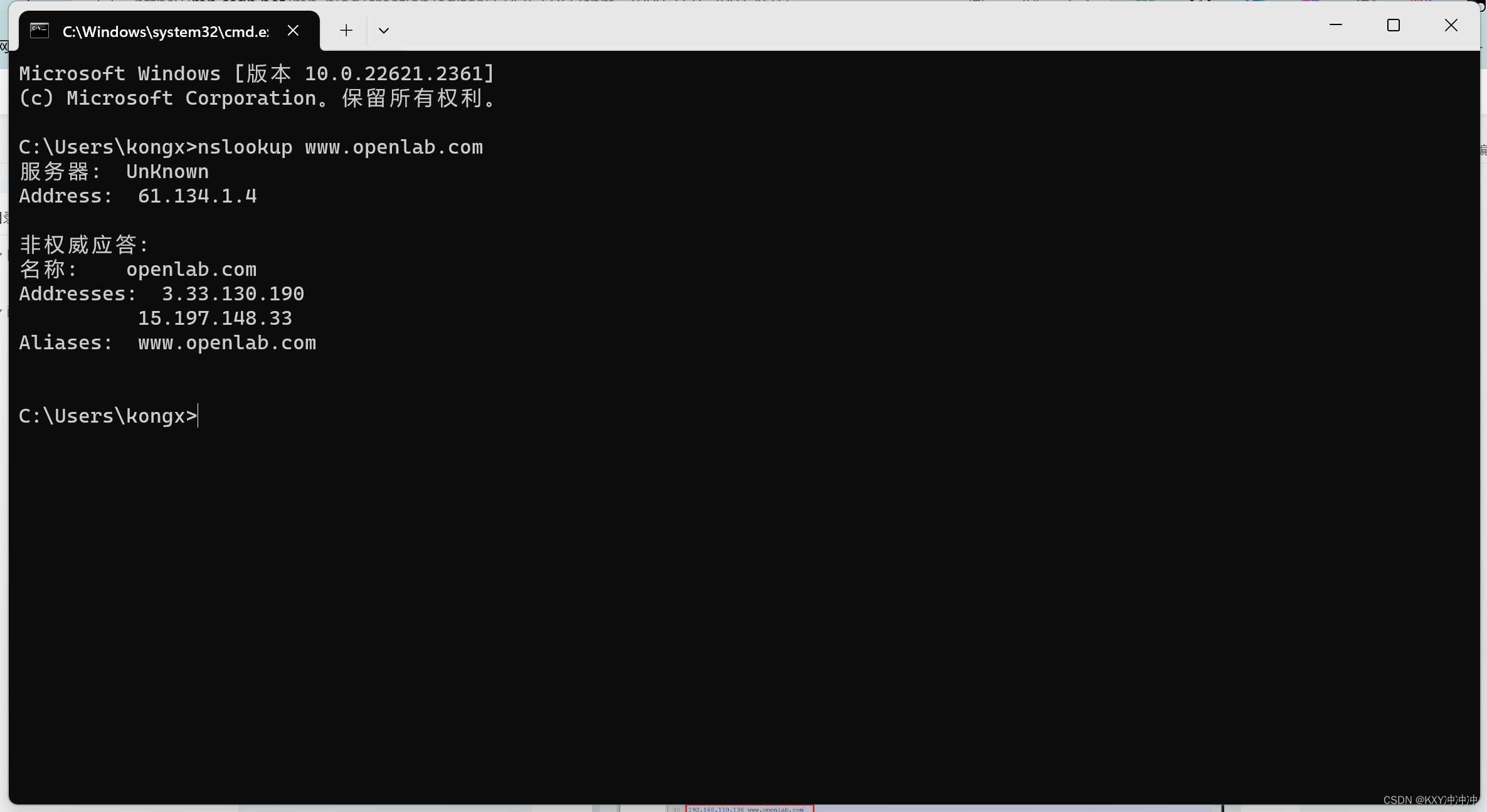
Web服务器实战
网站需求 1.基于域名www.openlab.com可以访问网站内容为 welcome to openlab!!! 2.给该公司创建三个网站目录分别显示学生信息,教学资料和缴费网站,基于www.openlab.com/student 网站访问学生信息,www.openlab.com/data网站访问教学资料 www…...

2021年电工杯数学建模B题光伏建筑一体化板块指数发展趋势分析及预测求解全过程论文及程序
2021年电工杯数学建模 B题 光伏建筑一体化板块指数发展趋势分析及预测 原题再现: 国家《第十四个五年规划和 2035 年远景目标纲要》中提出,将 2030 年实现“碳达峰”与 2060 年实现“碳中和”作为我国应对全球气候变暖的一个重要远景目标。光伏建筑一体…...

pandas教程:Essential Functionality 索引 过滤 映射 排序
文章目录 5.2 Essential Functionality(主要功能)1 Reindexing(重新索引)2 Dropping Entries from an Axis (按轴删除记录)3 Indexing, Selection, and Filtering(索引,选择,过滤)Selection with loc and i…...
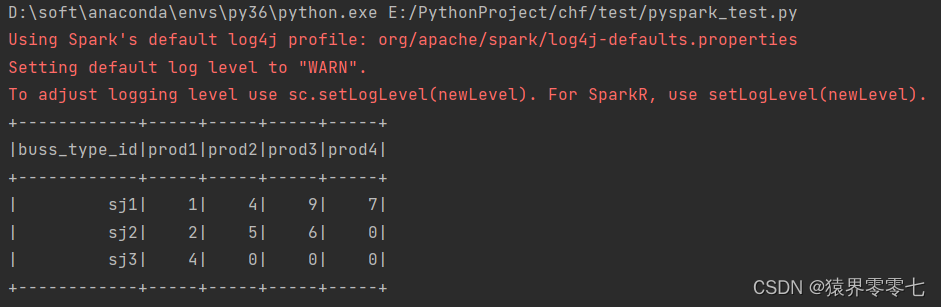
pyspark连接mysql数据库报错
使用pyspark连接mysql数据库代码如下 spark_conf SparkConf().setAppName("MyApp").setMaster("local")spark SparkSession.builder.config(confspark_conf).getOrCreate()url "jdbc:mysql://localhost:3306/test?useUnicodetrue&characterE…...

HK WEB3 MONTH Polkadot Hong Kong 火热报名中!
HK Web3 Month 11月除了香港金融科技周外,HK Web3 Month又是一大盛事,从10月29日开始开幕直到11月18日结束。此次将齐聚世界各地的Web3产业从业者、开发者、社群成员和学生来参与本次盛会。除外,超过75位产业知名的讲者与超过50场工作坊将为…...

“第六十三天”
这两天怎么做的这么别扭,为什么我的vs 的strlen函数包括终止字符了; 哦哦,明白了,fgets函数读取在未达到指定字长,或者遇见空白符之前,会读取前面的所有字符,所以会读取换行符,而get…...

常用排序算法实现
时间复杂度 O ( 1 ) O(1) O(1) void func1(int n){int count 100;count; } void func2(int n){int count 100;for(int i 0; i < count;i){} } int func3(int n){return n; }O ( n ) O(n) O(n) void func1(int n){int count 100;for(int i 0; i < n;i){count;} …...

使用表单登录方法模拟登录通信人家园,要求发送登录请求后打印出来的用户名下的用户组类别
目标网站:https://www.txrjy.com/forum.php 一、进入网页,右键“检查” 二、输入用户名和密码,点击“登录”,点击“Network”,上划加载项找到蓝色框中的内容 三、点击第一个加载项,找到URL 四、相关代码: …...
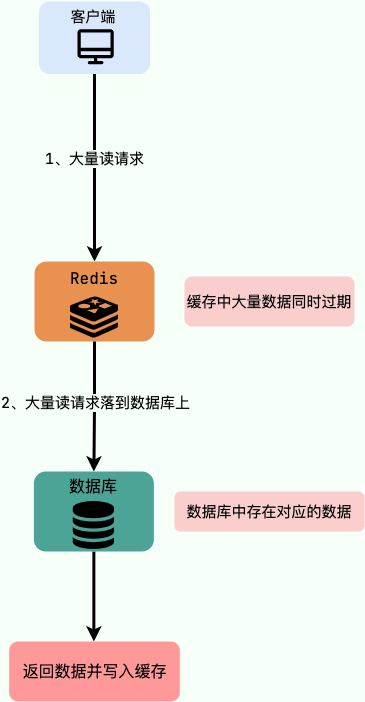
Redis 的缓存击穿,穿透,雪崩及其解决方案
1 缓存穿透 什么是缓存穿透? 大量请求的 key 是不合理的,根本不存在于缓存中,也不存在于数据库中 。导致这些请求直接到了数据库上,根本没有经过缓存这一层,对数据库造成了巨大的压力,可能直接就被这么多…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
