2021年电工杯数学建模B题光伏建筑一体化板块指数发展趋势分析及预测求解全过程论文及程序
2021年电工杯数学建模
B题 光伏建筑一体化板块指数发展趋势分析及预测
原题再现:
国家《第十四个五年规划和 2035 年远景目标纲要》中提出,将 2030 年实现“碳达峰”与 2060 年实现“碳中和”作为我国应对全球气候变暖的一个重要远景目标。光伏建筑一体化(BIPV)是充分利用工业建筑、公共建筑屋顶等资源实施分布式光伏发电工程,它对我国实现“碳达峰”和“碳中和”起到重要作用。目前已有北京、天津、上海、重庆、内蒙古、浙江等 31 地发布光伏建筑一体化未来三至五年相关政策,这将对光伏建筑一体化相关上市企业的发展带来一定影响。在股票交易软件中,每支股票都有日 K 线(由开盘价、收盘线、最高价、最低价构成),还有移动平均线(5 日、10 日、20 日等),通过对日 K 线和移动平均线的分析,可知每支股票的走势。股票市场中有板块指数(将同一板块的个股按不同的权重方式生成相关指数),它是对该板块走势的整体反映。现统计沪深股市中 37 家光伏建筑一体化相关企业的股票数据(见附件 1),将这 37 家企业股票看作一个整体称为光伏建筑一体化板块。光伏建筑一体化板块作为新兴板块,通过对板块指数发展趋势做出预测,可以了解板块相应行业未来的发展趋势。
请根据所给数据资料,解决以下问题:
1.利用附件 1 中数据,给出光伏建筑一体化板块指数的移动平均线(5 日、10 日、20 日等)模型,并绘制 2019 年 4 月 1 日至 2021 年 4 月 30 日该板块指数的移动平均线。
2.利用 2021 年 5 月 6 日至 5 月 28 日数据,对所建立模型进行误差分析并修正模型,根据修正后的模型对该板块未来发展趋势做出预测,给出 5 月 28 日后20 个交易日的日移动平均线、3 周的周移动平均线、2 个月的月移动平均线。
3.利用 2019 年 4 月 1 日至 2021 年 5 月 28 日数据,以 2 个月为一个时间段,对上证指数和光伏建筑一体化板块指数进行相关性分析。
4.对光伏建筑一体化板块个股投资风险进行评估,给出该板块 37 支股票2021 年 6 月份投资风险由低到高的排序结果。假定投资者持有资金 100 万元人民币,欲全部用于该板块的投资,请给出 2021 年 6 月份的最优投资方案(当日可用于投资的资金为上一个交易日结束后投资者所持有的资金,且每日持股数不超过 5 支)。
5.请给相关部门写一份不少于 1500 字关于我国光伏建筑一体化行业未来发展趋势的报告。
附件 1:沪深股市中 37 家光伏建筑一体化相关企业的股票数据
附件 2:http://www.csindex.com.cn/zh-CN/indices/index-rules中证指数有限公司
整体求解过程概述(摘要)
光伏建筑一体化指的是利用公共建筑、工业建筑的顶层布置光伏发电板,利用这些闲置资源来进行分布式光伏发电,以此实现“碳中和”目标。因此,对光伏建筑一体化的研究显得极为重要,本文针对光伏建筑一体化板块指数的发展趋势,建立了相关模型进行分析与预测。
针对问题一,首先建立了光伏建筑一体化板块指数的数学模型,通过平均加权求和的方式,将该板块 37 只股票的加权平均和作为板块指数。为了计算出板块指数的移动平均线,首先将板块指数的收盘价数据进行整理,如图 2 所示。据此绘制了板块指数的 5 日、10 日、20 日的移动平均线,如图 3 所示。然后以 5日移动平均线为例进行分析,建立了多幂次多项式数学模型,见式(3)。最后采用递推最小二乘法进行迭代求解,结果如图 4 所示,得到最终的模型见式(7)。
针对问题二,首先通过问题一模型对 2021 年 5.6~5.28 的移动平均线进行预测,然后与实际数据进行对比分析,结果如图 5 所示,此时平均误差为 1.2。然后通过 2021 年 5.6~5.28 时间段的数据对模型进行修正,同时修改模型的最大幂次,结果如图 6 所示,此时的平均误差为 0.2329,相比模型修正前的误差,修正后的平均误差同比下降了 80.6%。然后通过修正后的模型对未来数据进行预测,结果如图 7 所示。
针对问题三,由于上证指数和光伏建筑一体化指数的数值差异较大,因此首先对其进行归一化处理,然后利用加权平均的方式,建立了上证指数和光伏建筑一体化指数各自的综合指数模型,并对其进行求解,结果如图 8 所示。最后采用pearson 系数对二者指数进行相关性分析,结果如图 9 所示,其中 13 个时间段中,有 2 个时间段高度正相关;3 个时间段中度正相关;3 个时间段低度正相关;4个时间段不相关;1 个时间段中度负相关。
针对问题四,首先将将开盘价、最高价、最低价、收盘价数值与上一交易日的数值的差作为评价指标,然后以指标平均和的负数作为标准建立了综合评价模型,见式(12)。通过该模型对光伏一体化板块的 37 只股票进行了风险平均,结果如图 10 所示。其中,风险最低的 5 只股票依次是隆基股份、森特股份 、南玻A、中来股份 、 苏美达。最后通过风险程度,给出了投资者的最优投资方案,如表 2 所示。
针对问题五,根据本文研究结果和资料查询,给出了关于我国光伏建筑一体化行业未来发展趋势的报告。
模型假设:
1、假设搜集到的上证指数数据和附件所给数据真实有效。
2、假设数据预测时,不考虑其他突变因素的影响
3、假设 BIPV 板块的个股企业在预测时间内不会退市。
问题分析:
问题一分析
针对问题一,需建立出光伏建筑一体化板块指数移动平均线模型,首先,根据已知数据采用平均加权求和的方式得到板块指数中各变量的模型,进而可以得到板块指数中的收盘价,由题需绘制 5、10、20 日移动平均线,故分别以 5、10、20 为采样周期,得到对应的移动平均线,在此基础上,进一步建立多幂次多项式数学模型来表示板块指数移动平均线模型,通过求解得到该模型系数结果。
问题二分析
针对问题二,需利用 2021 年 5 月 6 日至 5 月 28 日的数据,来分析问题一中所建模型的误差并进行修正,由于该时间段内的数据较少,利用 10 日、20 日移动平均线模型进行预测时可验证的数据不足,因此,本问主要考虑利用问题一中所建立的 5 日移动平均线模型进行预测,通过与实际值进行对比,从而可以得到模型的预测误差,完成误差分析,根据题意得,需利用 5 月 6 日至 5 月 28 日的数据对模型进行修正,因此,考虑将此段时间内实际数据代入问题一所建立的多幂次多项式数学模型中,可以利用递推最小二乘法重新求得最优系数,完成对模型的修正,进而利用修正后的模型重新进行预测。
问题三分析
针对问题三,需分析上证指数和光伏建筑一体化板块指数的相关性,根据相关性定理,需先分别求得两者指数的一个代表性指标,再利用相关系数计算公式在求得相关性,考虑到两者指数中包括多个指标且每个指标差异较大,因此,先分别将两者的各个指标进行归一化处理并加权求和,来得到两者的综合指数,根据题目要求,需以两个月为一个时间段,故将总时间分成 13 段,分别进行相关性分析。
问题四分析
针对问题四,需对板块中 37 支股票进行风险评估,本问考虑当股票波动较大时,其风险也会较大,因此选取个股指数中的开盘价、最高价、最低价以及收盘价作为评价指标,但考虑到每个指标差异较大,故重新选取该指标当前时刻数值与上一时刻数值的差值作为新的评价指标,在此基础上进行加权平均,得到个股的风险评价模型,由于该模型主要包括个股指数两个时刻的差值,即变化量,因此,判断模型计算值越大,则风险越高,反之越低,最后选取风险评价值最低的 5 支按比例分配投资资金即可。
问题五分析
针对问题五,通过查阅相关资料,了解光伏建筑一体化的概念以及发展现状,根据本文对于该板块股市的分析,进一步分析该板块未来发展趋势,并提出相关建议。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
部分程序如下:
%先求时延和嵌入维,带入本程序,Lyapunov_rosenstein_2.dll调用需要安装完整Simulink功能
% 计算时间序列 Lyapunov 指数
clc
clear
close all
data = textread('深证.txt'); % 时间序列,列向量
data = data(end-2000:end);
%-----------------------------------------------------------------
% Logistic 入口参数
tau = 2; % 时延
m = 25; % 嵌入维
[xn] = PhaSpaRecon(data,tau,m); % 每列为一个点
xn = xn'; % 每行为一个点
P =fix(period_mean_fft(data)); % 序列平均周期
if P>500P=500;
end
taumax = 500; % 最大离散步进时间
fs = 1; % 采样频率
Y = Lyapunov_rosenstein_2(xn,fs,tau,m,taumax,P);
Y(1)=[];
figure
plot(log(Y),'b-'); grid; xlabel('i'); ylabel('y(i)');
linear_zone=[1:length(Y)]';
F = polyfit(linear_zone,log(Y),1);
y=linear_zone.*F(1)+F(2);
hold on
plot(linear_zone,y,'r-')
legend('data','线性')
str = ['y=',num2str(F(1)),'x+(',num2str(F(2)),')'];
text(50,max(y),str)
clear
clc
%cao法求嵌入维
data = textread('深证.txt'); % 时间序列,列向量
data = data(end-100:end);
min_m=1;
max_m=30;
tau=2;
k=1;
N=length(data);
En=[];
for m=min_m:max_mNm=N-tau*(m-1);Y=[];D=[];ad=[];Y=reconstitution(data,N,m,tau);for i=1:N-m*taud=[];for j=1:N-m*taud(j)=norm(Y(:,i)-Y(:,j),inf);endtemp=[];temp=sort(d);D(i,1)=i; temp1=[];temp2=[];temp1=find(temp>0);temp2=find(d==temp(temp1(1)));D(i,2)=temp2(1); D(i,3)=temp(temp1(1));%计算a(i,m)Y1=[];Y2=[];Y1=[Y(:,i);data(m*tau+i)];Y2=[Y(:,D(i,2));data(D(i,2)+m*tau)];ad(i)=norm(Y1-Y2,inf)/D(i,3);end%求E(d)E(k,1)=m;E(k,2)=sum(ad)/(N-m*tau);%求E*(d)En(k,1)=m;dd=[];for kk=1:N-m*taudd(kk)=abs(data(D(kk,1)+m*tau)-data(D(kk,2)+m*tau));endEn(k,2)=sum(dd)/(N-m*tau);k=k+1;
end
%求E1(d)
E1=[];
for i=1:(max_m-min_m)E1(i,1)=E(i,1);E1(i,2)=E(i+1,2)/E(i,2);
end
%求E2(d)
E2=[];
for i=1:(max_m-min_m)E2(i,1)=En(i,1);E2(i,2)=En(i+1,2)/En(i,2);
end
figure(1)
plot(E1(:,1),E1(:,2),'-bs',E2(:,1),E2(:,2),'-r*');xlabel('嵌入维数');ylabel('E1(m)&E2(m)');
grid on
function [xn,dn] = PhaSpaRecon(s,tau,m,T)
% 混沌序列的相空间重构 (phase space reconstruction)
% [xn, dn, xn_cols] = PhaSpaRecon(s, tau, m)
% 输入参数: s 混沌序列(列向量)
% tau 重构时延
% m 重构维数
% T 直接预测步数
% 输出参数: xn 相空间中的点序列(每一列为一个点)
% dn 一步预测的目标(行向量)[rows,cols] = size(s);
if (rows>cols)len = rows;s = s';
elselen = cols;
endif (nargin < 4)T = 1;
endif (nargout==1)if (len-(m-1)*tau < 1)disp('err: delay time or the embedding dimension is too large!')xn = [];elsexn = zeros(m,len-(m-1)*tau);for i = 1:mxn(i,:) = s(1+(i-1)*tau : len-(m-i)*tau); % 相空间重构,每一行为一个点 endendelseif (nargout==2)if (len-T-(m-1)*tau < 1)disp('err: delay time or the embedding dimension is too large!')xn = [];dn = [];elsexn = zeros(m,len-T-(m-1)*tau);for i = 1:mxn(i,:) = s(1+(i-1)*tau : len-T-(m-i)*tau); % 相空间重构,每一行为一个点 enddn = s(1+T+(m-1)*tau : end); % 预测的目标endend
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2021年电工杯数学建模B题光伏建筑一体化板块指数发展趋势分析及预测求解全过程论文及程序
2021年电工杯数学建模 B题 光伏建筑一体化板块指数发展趋势分析及预测 原题再现: 国家《第十四个五年规划和 2035 年远景目标纲要》中提出,将 2030 年实现“碳达峰”与 2060 年实现“碳中和”作为我国应对全球气候变暖的一个重要远景目标。光伏建筑一体…...

pandas教程:Essential Functionality 索引 过滤 映射 排序
文章目录 5.2 Essential Functionality(主要功能)1 Reindexing(重新索引)2 Dropping Entries from an Axis (按轴删除记录)3 Indexing, Selection, and Filtering(索引,选择,过滤)Selection with loc and i…...
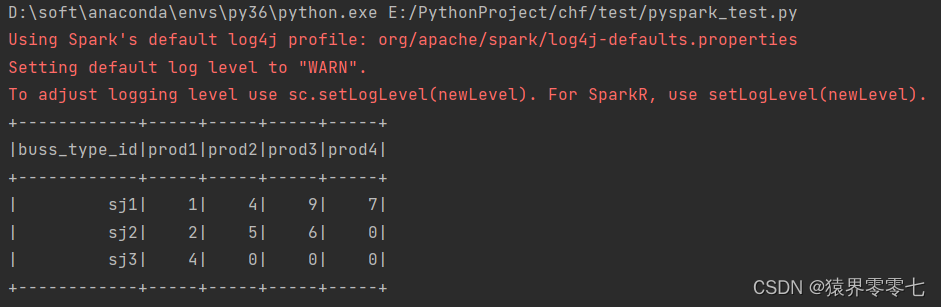
pyspark连接mysql数据库报错
使用pyspark连接mysql数据库代码如下 spark_conf SparkConf().setAppName("MyApp").setMaster("local")spark SparkSession.builder.config(confspark_conf).getOrCreate()url "jdbc:mysql://localhost:3306/test?useUnicodetrue&characterE…...

HK WEB3 MONTH Polkadot Hong Kong 火热报名中!
HK Web3 Month 11月除了香港金融科技周外,HK Web3 Month又是一大盛事,从10月29日开始开幕直到11月18日结束。此次将齐聚世界各地的Web3产业从业者、开发者、社群成员和学生来参与本次盛会。除外,超过75位产业知名的讲者与超过50场工作坊将为…...

“第六十三天”
这两天怎么做的这么别扭,为什么我的vs 的strlen函数包括终止字符了; 哦哦,明白了,fgets函数读取在未达到指定字长,或者遇见空白符之前,会读取前面的所有字符,所以会读取换行符,而get…...

常用排序算法实现
时间复杂度 O ( 1 ) O(1) O(1) void func1(int n){int count 100;count; } void func2(int n){int count 100;for(int i 0; i < count;i){} } int func3(int n){return n; }O ( n ) O(n) O(n) void func1(int n){int count 100;for(int i 0; i < n;i){count;} …...

使用表单登录方法模拟登录通信人家园,要求发送登录请求后打印出来的用户名下的用户组类别
目标网站:https://www.txrjy.com/forum.php 一、进入网页,右键“检查” 二、输入用户名和密码,点击“登录”,点击“Network”,上划加载项找到蓝色框中的内容 三、点击第一个加载项,找到URL 四、相关代码: …...
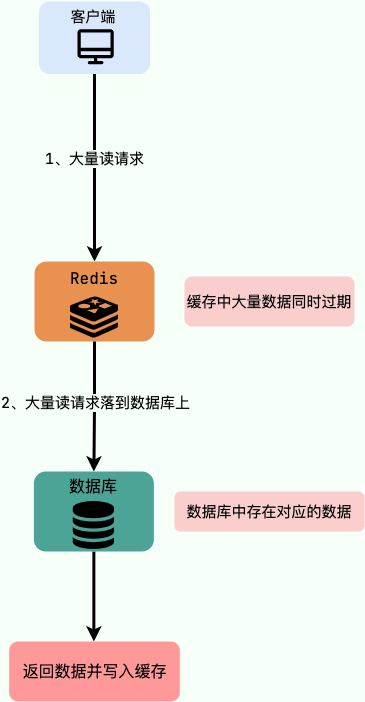
Redis 的缓存击穿,穿透,雪崩及其解决方案
1 缓存穿透 什么是缓存穿透? 大量请求的 key 是不合理的,根本不存在于缓存中,也不存在于数据库中 。导致这些请求直接到了数据库上,根本没有经过缓存这一层,对数据库造成了巨大的压力,可能直接就被这么多…...
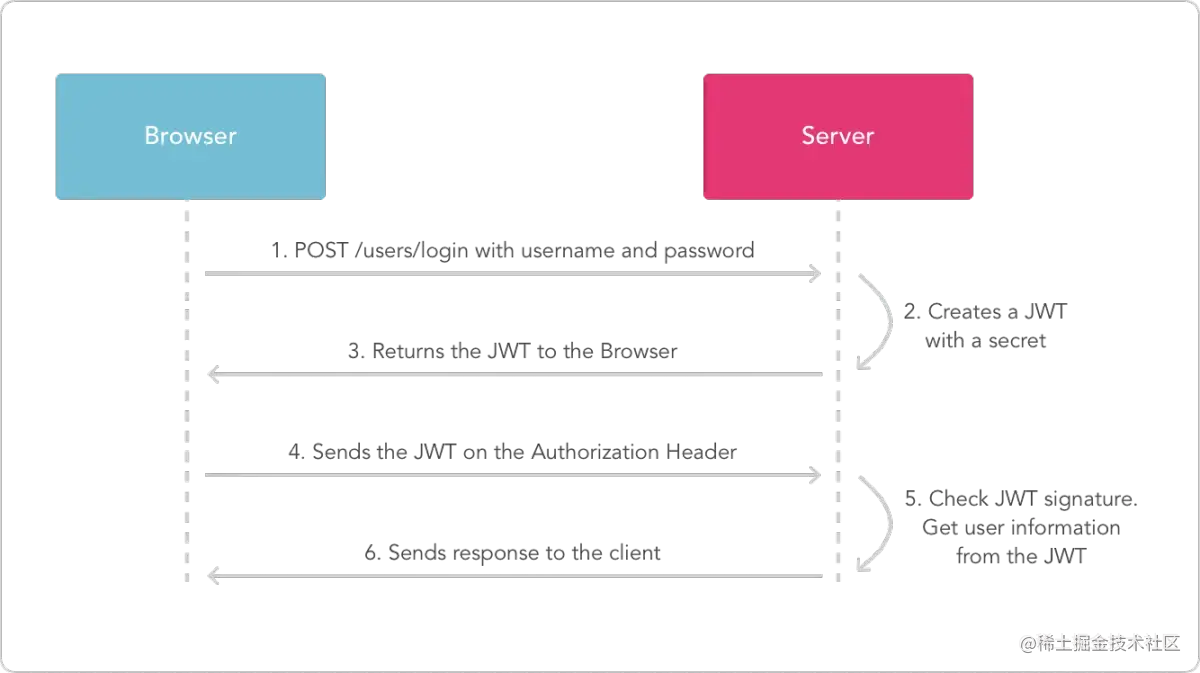
JWT原理分析——JWT
了解为什么会有JWT的出现? 首先不得不提到一个知识叫做跨域身份验证,JWT的出现就是为了更好的解决这个问题,但是在没有JWT的时候,我们一般怎么做呢?一般使用Cookie和Session,流程大体如下所示:…...
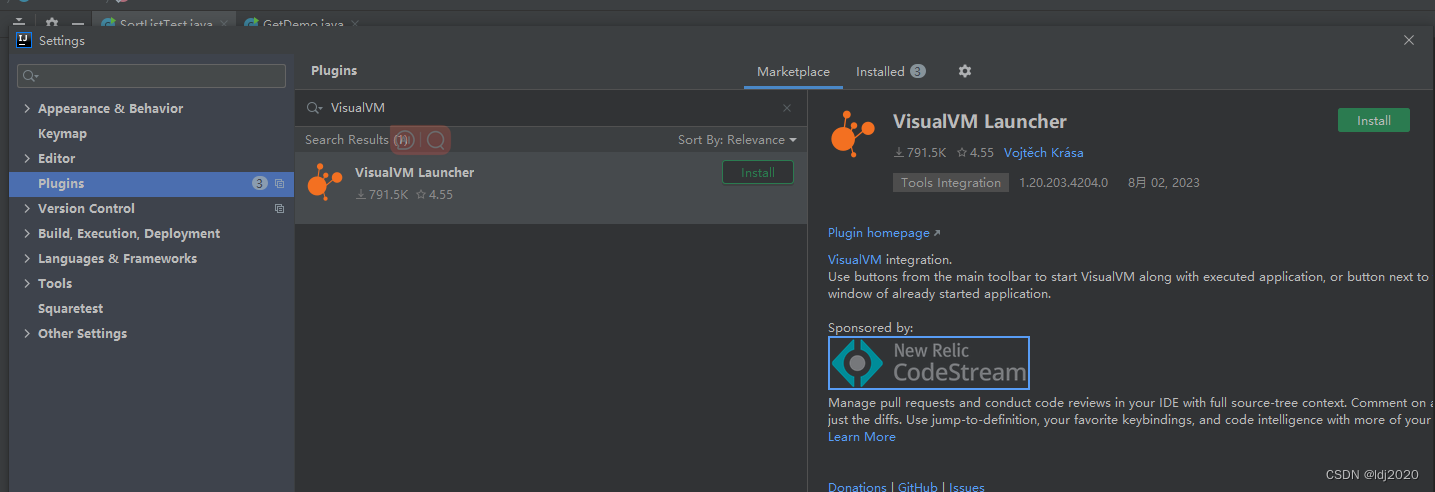
Jprofiler/ VisualVM 定位内存溢出OOM
下载,接受协议下一步下一步,最后选择与IDEA集成OK ej-technologies - Java APM, Java Profiler, Java Installer Builder IDEA配置参数: # F:\study\spring-test\dump 为dump文件保存路径-XX:HeapDumpOnOutOfMemoryError -XX:HeapDumpPathF:\study\spring-test\dumppackage …...

NOIP2023模拟13联测34 competition
题目大意 有一场题目数量为 m m m的比赛,有一个团队想要来参加。 这个团队有 n n n个选手,编号为 i i i的选手能做第 l i ∼ r i l_i \sim r_i li∼ri道题,每题他都有 100 % 100\% 100%的概率做出来。 这个团队会随机派出一只队伍来参…...
Intel oneAPI笔记(2)--jupyter官方文档(oneAPI_Intro)学习笔记
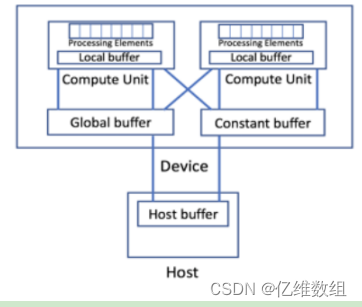
前言 本文是对jupyterlab中oneAPI_Essentials/01_oneAPI_Intro文档的学习记录,包含对SYCL、DPC extends SYCL、oneAPI Programming models等介绍和SYCL代码的初步演示等内容 oneAPI编程模型综述 oneAPI编程模型提供了一个全面而统一的开发人员工具组合࿰…...
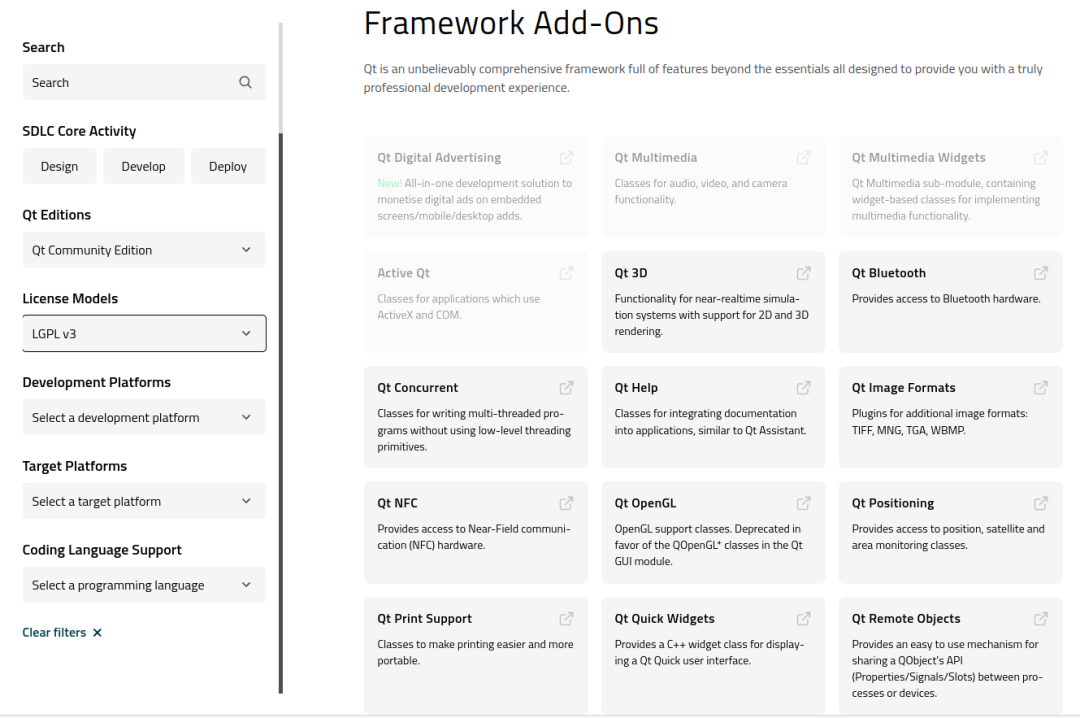
用 QT 开发软件会吃官司吗?
之前我写过我们现在使用 QT 开发跨平台软件,有朋友留言,QT 虽好,当心收到律师函。今天就来聊聊这个话题。 在开始这个话题之前,我们先把使用盗版 QT 排除在外,只讨论在合法且遵从版权协议的前提下,能否使用…...

远程运维用什么软件?可以保障更安全?
远程运维顾名思义就是通过远程的方式IT设备等运行、维护。远程运维适用场景包含因疫情居家办公,包含放假期间出现运维故障远程解决,包含项目太远需要远程操作等等。但远程运维过程存在一定风险,安全性无法保障,所以一定要选择靠谱…...

数据结构与算法C语言版学习笔记(2)-线性表、顺序存储结构的线性表
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 数据结构部分的知识框架一、线性表的定义和特点1.定义2.特点 二、线性表的实际案例引入1.案例一:多项式的加减乘除2.案例二:当多项式是稀疏多…...
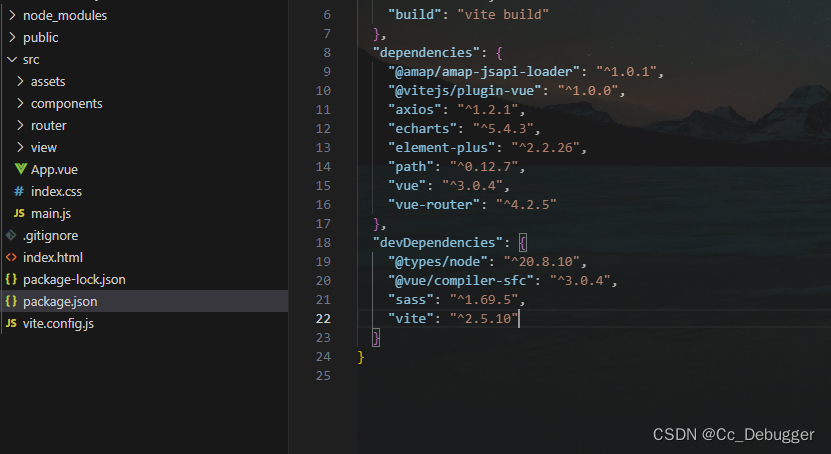
【vite】vite.defineConfig is not a function/npm无法安装第三方包问题
当使用vite命令 npm init vite-app 项目名称时配置 import vue from vitejs/plugin-vueexport default defineConfig({plugins: [vue()] })会报错vite.defineConfig is not a function 还有就是npm下载的时候也会报错 原因vite插件vitejs/plugin-vue和vite版本问题 解决 调…...

234. 回文链表 --力扣 --JAVA
题目 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。 解题思路 判断链表是否为回文链表取决于链表中各个节点的值,所以可以通过存储各节点的值进行对比判断&…...
【JAVA学习笔记】65 - 文件类,IO流--节点流、处理流、对象流、转换流、打印流
项目代码 https://github.com/yinhai1114/Java_Learning_Code/tree/main/IDEA_Chapter19/src/com/yinhai 文件 一、文件,流 文件,对我们并不陌生,文件是保存数据的地方,比如大家经常使用的word文档,txt文件,excel文件..都是文件。它既可以保存一张图片…...

R语言 复习 习题图片
这是日天土申哥不知道从哪淘来的R语言复习知识点图片,大部分内容都是课后习题的答案 加油吧,骚年,考个好分数...
c语言 结构体 简单实例
结构体 简单例子 要求: 结构体保存学生信息操作 代码 #include <stdio.h>//定义结构体 struct student{int ID;char name[20];char sex;char birthday[8];int grade; };int main(){int number;printf("请输入学生个数:");scanf(&quo…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...
