当前位置： 首页 > news >正文

Vue 嵌套路由 多级路由规则

news 2026/2/9 10:27:37

套娃路由

routes:[{path: '/login',component: Login},{path: '/user',component: User,children:[{ path: 'test', component: Test },{ path: 'test2', component: Test2 },]}]

子路由不需要加/

在父组件

子路由不需要加/ 需要带上父亲的路由路径

 <router-link  to="user/test" >跳转用户</router-link><router-view></router-view><!-- 路由器占位符 -->

相关文章：

Vue 嵌套路由 多级路由规则

套娃路由 routes:[{path: /login,component: Login},{path: /user,component: User,children:[{ path: test, component: Test },{ path: test2, component: Test2 },]}]子路由不需要加/ 在父组件 子路由不需要加/ 需要带上父亲的路由路径 <router-link to"user/test…...

编程日记 2023/11/8 8:56:50

pandas教程：Introduction to pandas Data Structures pandas的数据结构

文章目录 Chapter 5 Getting Started with pandas5.1 Introduction to pandas Data Structures1 Series2 DataFrame3 Index Objects (索引对象) Chapter 5 Getting Started with pandas 这样导入pandas&#xff1a; import pandas as pde:\python3.7\lib\site-packages\numpy…...

编程日记 2023/11/8 8:55:49

MinIO 分布式文件(对象)存储

简介 MinIO是高性能、可扩展、云原生支持、操作简单、开源的分布式对象存储产品。 在中国&#xff1a;阿里巴巴、腾讯、百度、中国联通、华为、中国移动等等9000多家企业也都在使用MinIO产品 官网地址&#xff1a;http://www.minio.org.cn/ 下载 官网下载(8.4.3版本)&#x…...

编程日记 2023/11/8 8:54:48

HTML表单标签

## HTML标签&#xff1a;表单标签 * 表单&#xff1a; * 概念&#xff1a;用于采集用户输入的数据的。用于和服务器进行交互。 * form&#xff1a;用于定义表单的。可以定义一个范围&#xff0c;范围代表采集用户数据的范围 * 属性&#xff1…...

编程日记 2023/11/8 8:51:45

【黑马程序员】SpringCloud——Eureka

文章目录 前言一、提供者与消费者1. 服务调用关系 二、远程调用的问题三、eureka 原理分析1. eureka 的作用 四、Eureka 案例1. 搭建 eureka 服务1. 服务注册1.1 注册 user-service1.2 启动 user-service3. order-service 完成服务注册 3. 服务发现1. 在 order-service 完成服务…...

编程日记 2023/11/8 8:50:44

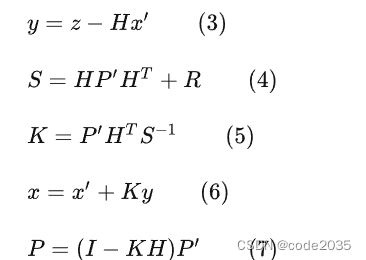
目标跟踪（DeepSORT）

本文首先将介绍在目标跟踪任务中常用的匈牙利算法&#xff08;Hungarian Algorithm&#xff09;和卡尔曼滤波&#xff08;Kalman Filter&#xff09;&#xff0c;然后介绍经典算法DeepSORT的工作流程以及对相关源码进行解析。 目前主流的目标跟踪算法都是基于Tracking-by-Detec…...

编程日记 2023/11/8 8:49:43

2 任务2： 使用趋动云GPU进行猫狗识别实践

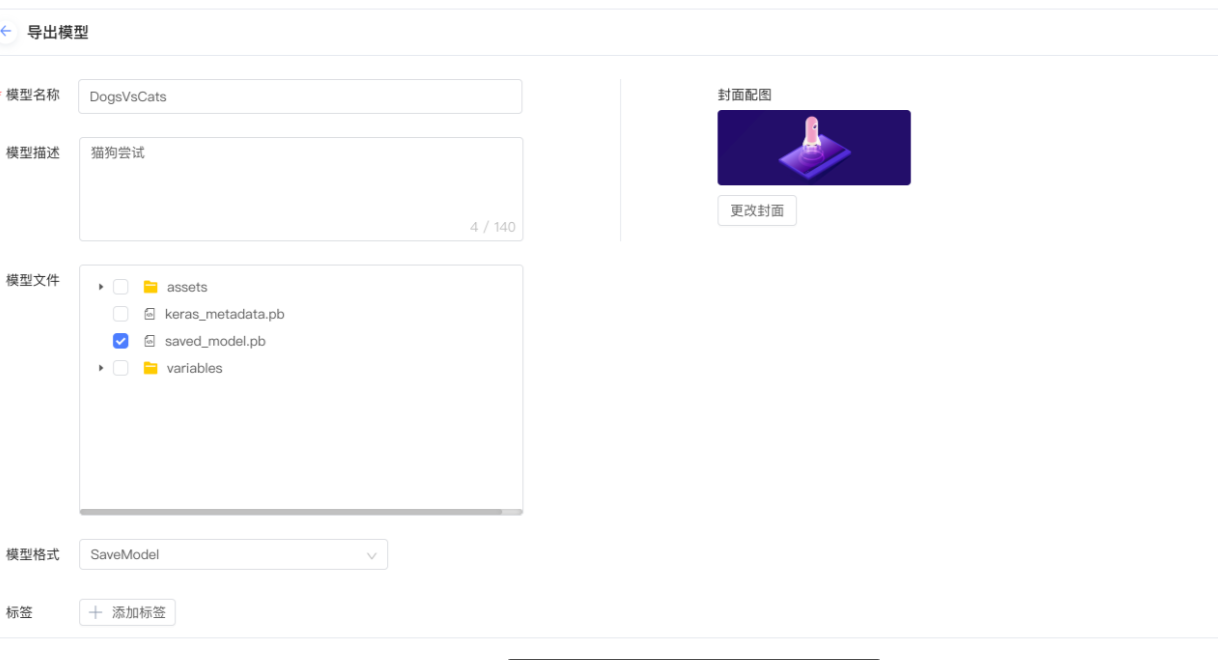
使用趋动云GPU进行猫狗识别实践 1 创建项目2 初始化开发环境3 调试代码4 提交离线任务5 结果集存储与下载 使用趋动云提供的免费GPU&#xff0c;进行猫狗识别实践。 虽然例程里面提供的是基于tensorflow的&#xff0c;但是你也可以使用pytorch的代码 使用这个平台的一个优点就是…...

编程日记 2023/11/8 8:48:42

技术分享 | app自动化测试（Android）--显式等待机制

WebDriverWait类解析 WebDriverWait 用法代码 Python 版本 WebDriverWait( driver,timeout,poll_frequency0.5,ignored_exceptionsNone) 参数解析&#xff1a; driver&#xff1a;WebDriver 实例对象 timeout: 最长等待时间&#xff0c;单位秒 poll_frequency: 检测的间…...

编程日记 2023/11/8 8:47:41

机器学习基础之《回归与聚类算法（5）—分类的评估方法》

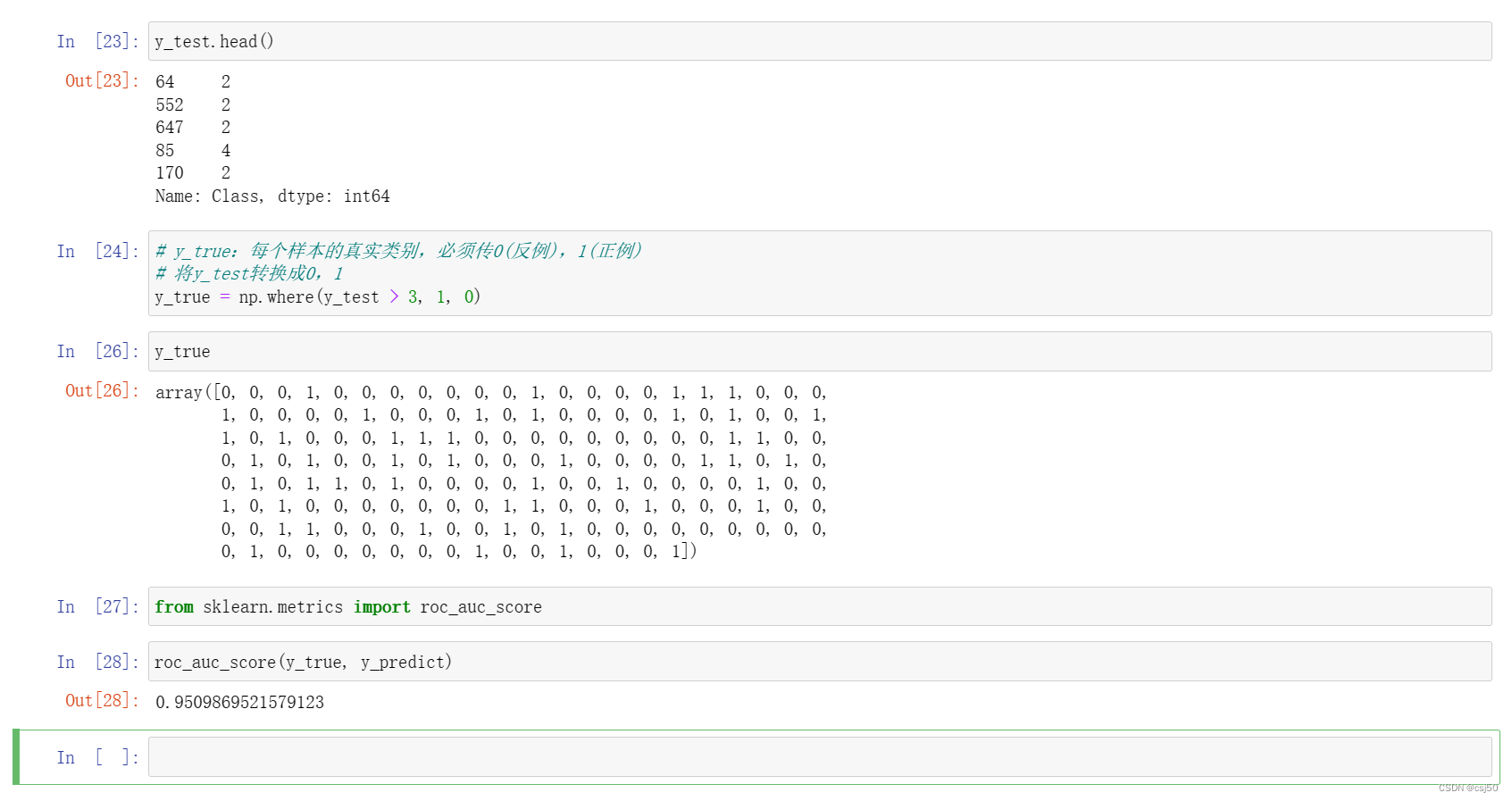
问题&#xff1a;上一篇的案例&#xff0c;真的患癌症的&#xff0c;能被检查出来的概率&#xff1f; 一、精确率和召回率 1、混淆矩阵 在分类任务下&#xff0c;预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合&#xff0c;构成混淆矩阵(适…...

编程日记 2023/11/8 8:46:40

如何在macbook上删除文件？Mac删除文件的多种方法

在使用MacBook电脑时&#xff0c;桌面上经常会积累大量的文件&#xff0c;而这些文件可能已经不再需要或已经过时。为了保持桌面的整洁和提高电脑性能&#xff0c;我们需要及时删除这些文件。本文将介绍MacBook怎么删除桌面文件&#xff0c;以及macbook删除桌面文件快捷键。 一…...

编程日记 2023/11/8 8:45:39

Java代码Demo——Map根据key或value排序

Map根据key排序 升序 Demo代码&#xff1a; //使用TreeMap Map<Integer, String> map new TreeMap<>(); map.put(10, "第10名次"); map.put(15, "第15名次"); map.put(1, "第1名次"); map.put(5, "第5名次"); map.put…...

编程日记 2023/11/8 8:44:37

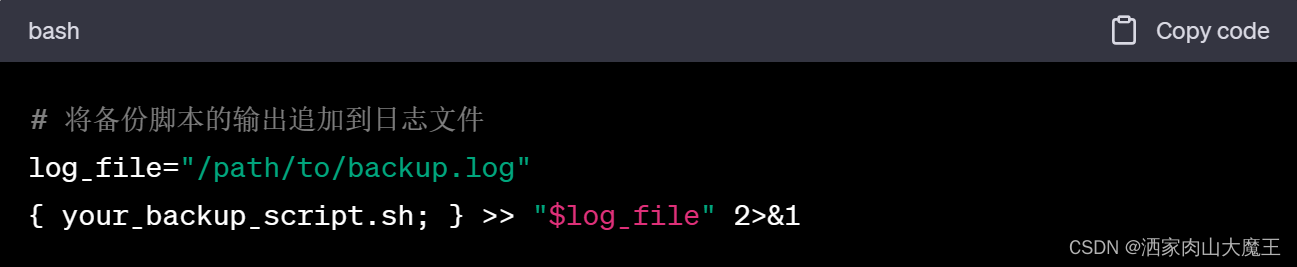
一个Linux自动备份脚本的示例

一个简单的Linux自动备份脚本的示例&#xff0c;根据需要进行自定义&#xff1a; 请确保按照您的需求修改source_dir和backup_dir为要备份的源目录和备份目录的路径。此脚本使用tar命令创建一个以当前日期命名的压缩备份文件&#xff0c;并在备份完成后检查是否成功。此外&…...

编程日记 2023/11/8 8:43:36

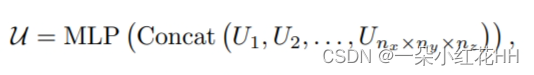
[论文阅读]PV-RCNN++

PV-RCNN PV-RCNN: Point-Voxel Feature Set Abstraction With Local Vector Representation for 3D Object Detection 论文网址&#xff1a;PV-RCNN 论文代码&#xff1a;PV-RCNN 简读论文 这篇论文提出了两个用于3D物体检测的新框架PV-RCNN和PV-RCNN,主要的贡献如下: 提出P…...

编程日记 2023/11/8 8:42:35

测试老鸟整理，Postman加密接口测试-Rsa/Aes对参数加密（详细总结）

目录&#xff1a;导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结&#xff08;尾部小惊喜&#xff09; 前言 一些问题 postma…...

编程日记 2023/11/8 8:40:33

JavaScript使用对象

对象(object)是最基本、最通用的类型&#xff0c;具有复合性结构&#xff0c;属于引用型数据&#xff0c;对象的结构具有弹性&#xff0c;内部的数据是无序的&#xff0c;每个成员被称为属性。在JavaScript中&#xff0c;对象是一个泛化的概念&#xff0c;任何值都可以转换为对…...

编程日记 2023/11/8 8:38:30

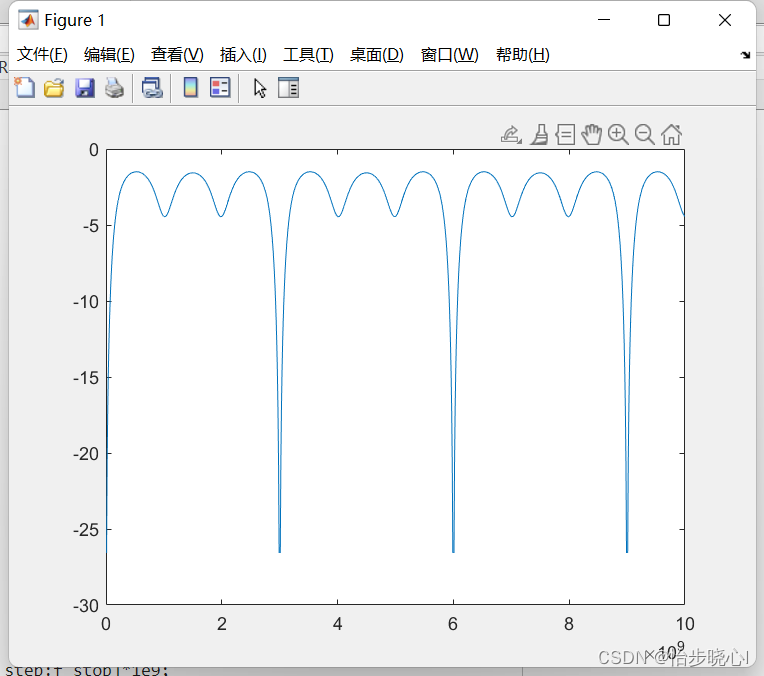
微带线的ABCD矩阵的推导、转换与级联-Matlab计算实例

微带线的ABCD矩阵的推导、转换与级联-Matlab计算实例 散射参数矩阵有实际的物理意义&#xff0c;但是其无法级联计算&#xff0c;但是ABCD参数和传输散射矩阵可以级联计算&#xff0c;在此先简单介绍ABCD参数矩阵的基本用法。 1、微带线的ABCD矩阵的推导 其他的一些常用的二端…...

编程日记 2023/11/8 8:37:29

“网站不安全”该如何解决

当我们的网站被客户访问的时候&#xff0c;经常会出现提示不安全的情况&#xff0c;导致客户的不信任&#xff0c;从而出现客户流失的现象&#xff0c;这种情况我们应该如何解决呢&#xff1f; 首先&#xff0c;我们要确定网站会出现不安全的原因&#xff0c;一般来说&#xff…...

编程日记 2023/11/8 8:35:28

gitlab数据备份和恢复

gitlab数据备份 sudo gitlab-rake gitlab:backup:create备份文件默认存放在/var/opt/gitlab/backups路径下&#xff0c; 生成1697101003_2023_10_12_12.0.3-ee_gitlab_backup.tar 文件 gitlab数据恢复 sudo gitlab-rake gitlab:backup:restore BACKUP1697101003_2023_10_12_…...

编程日记 2023/11/8 8:34:27

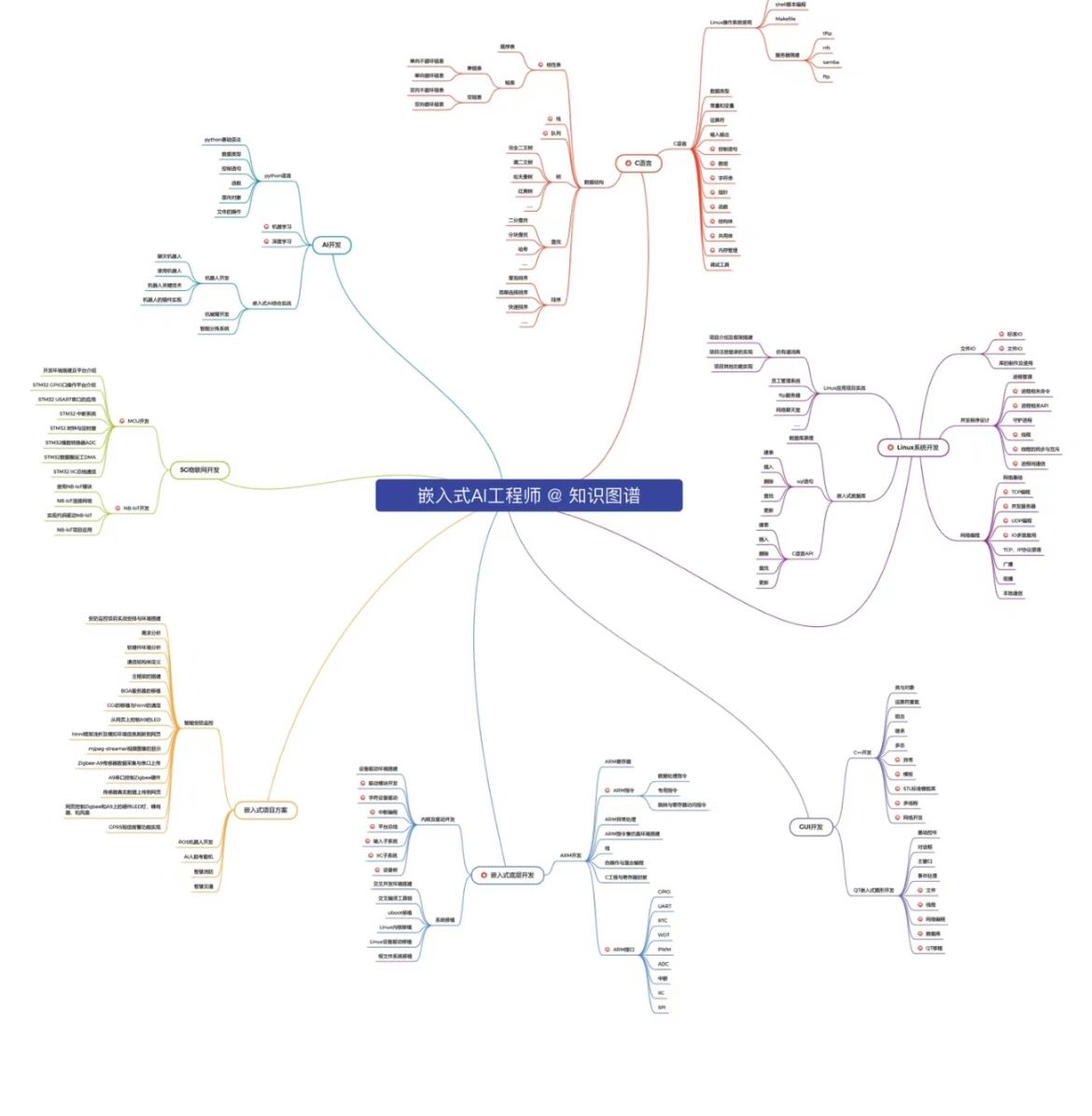
嵌入式Linux和stm32区别? 之间有什么关系吗？

嵌入式Linux和stm32区别? 之间有什么关系吗&#xff1f; 主要体现在以下几个方面&#xff1a; 1.硬件资源不同 单片机一般是芯片内部集成flash、ram&#xff0c;ARM一般是CPU&#xff0c;配合外部的flash、ram、sd卡存储器使用。最近很多小伙伴找我&#xff0c;说想要一些嵌…...

编程日记 2023/11/8 8:33:26

【Redis】String字符串类型-内部编码使用场景

文章目录 内部编码使用场景缓存功能计数功能共享会话手机验证码 内部编码 字符串类型的内部编码有3种&#xff1a; int&#xff1a;8个字节&#xff08;64位&#xff09;的⻓整型&#xff0c;存储整数embstr&#xff1a;压缩字符串&#xff0c;适用于表示较短的字符串raw&…...

编程日记 2023/11/8 8:31:23

wordpress后台更新后 前端没变化的解决方法

使用siteground主机的wordpress网站&#xff0c;会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后&#xff0c;网站没有变化的情况。 不熟悉siteground主机的新手&#xff0c;遇到这个问题&#xff0c;就很抓狂&#xff0c;明明是哪都没操作错误&#x…...

编程新知 2026/2/9 2:42:46

使用VSCode开发Django指南

使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架&#xff0c;专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用&#xff0c;其中包含三个使用通用基本模板的页面。在此…...

编程新知 2026/2/8 16:24:38

逻辑回归：给不确定性划界的分类大师

想象你是一名医生。面对患者的检查报告&#xff08;肿瘤大小、血液指标&#xff09;&#xff0c;你需要做出一个**决定性判断**&#xff1a;恶性还是良性&#xff1f;这种“非黑即白”的抉择&#xff0c;正是**逻辑回归&#xff08;Logistic Regression&#xff09;** 的战场&a…...

编程新知 2025/10/27 21:25:04

三维GIS开发cesium智慧地铁教程（5）Cesium相机控制

一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点&#xff1a; 路径验证&#xff1a;确保相对路径.…...

编程新知 2025/12/1 19:23:04

《Playwright：微软的自动化测试工具详解》

Playwright 简介:声明内容来自网络&#xff0c;将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具&#xff0c;支持 Chrome、Firefox、Safari 等主流浏览器&#xff0c;提供多语言 API&#xff08;Python、JavaScript、Java、.NET&#xff09;。它的特点包括&a…...

编程新知 2025/7/23 15:00:00

ESP32 I2S音频总线学习笔记（四）： INMP441采集音频并实时播放

简介 前面两期文章我们介绍了I2S的读取和写入&#xff0c;一个是通过INMP441麦克风模块采集音频&#xff0c;一个是通过PCM5102A模块播放音频&#xff0c;那如果我们将两者结合起来&#xff0c;将麦克风采集到的音频通过PCM5102A播放&#xff0c;是不是就可以做一个扩音器了呢…...

编程新知 2026/2/5 8:19:14

相机从app启动流程

一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下： 重点代码分析： 启动相机前，先要通过getCameraIdList获取camera的个数以及id，然后可以通过getCameraCharacteristics获取对应id camera的capabilities（静态信息）进行一些openCamera前的…...

编程新知 2026/1/31 5:09:19

面向无人机海岸带生态系统监测的语义分割基准数据集

描述&#xff1a;海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而&#xff0c;目前该领域仍面临一个挑战&#xff0c;即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

编程新知 2026/1/25 14:15:52

spring Security对RBAC及其ABAC的支持使用

RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型&#xff0c;它将权限分配给角色&#xff0c;再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

编程新知 2026/2/6 14:22:43

Python训练营-Day26-函数专题1：函数定义与参数

题目1&#xff1a;计算圆的面积 任务&#xff1a; 编写一个名为 calculate_circle_area 的函数&#xff0c;该函数接收圆的半径 radius 作为参数&#xff0c;并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求&#xff1a;函数接收一个位置参数 radi…...

编程新知 2026/1/31 0:07:38