基于斑马算法的无人机航迹规划-附代码
基于斑马算法的无人机航迹规划
文章目录
- 基于斑马算法的无人机航迹规划
- 1.斑马搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用斑马算法来优化无人机航迹规划。
1.斑马搜索算法
斑马算法原理请参考:https://blog.csdn.net/u011835903/article/details/130565746
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得斑马搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用斑马算法对航迹评价函数式(7)进行优化。优化结果如下:


从结果来看,斑马算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于斑马算法的无人机航迹规划-附代码
基于斑马算法的无人机航迹规划 文章目录 基于斑马算法的无人机航迹规划1.斑马搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用斑马算法来优化无人机航迹规划。 1.斑马搜索算法 …...

干货 | 接口自动化测试分层设计与实践总结
接口测试三要素: 参数构造 发起请求,获取响应 校验结果 一、原始状态 当我们的用例没有进行分层设计的时候,只能算是一个“苗条式”的脚本。以一个后台创建商品活动的场景为例,大概流程是这样的(默认已经是登录状态下)&#…...
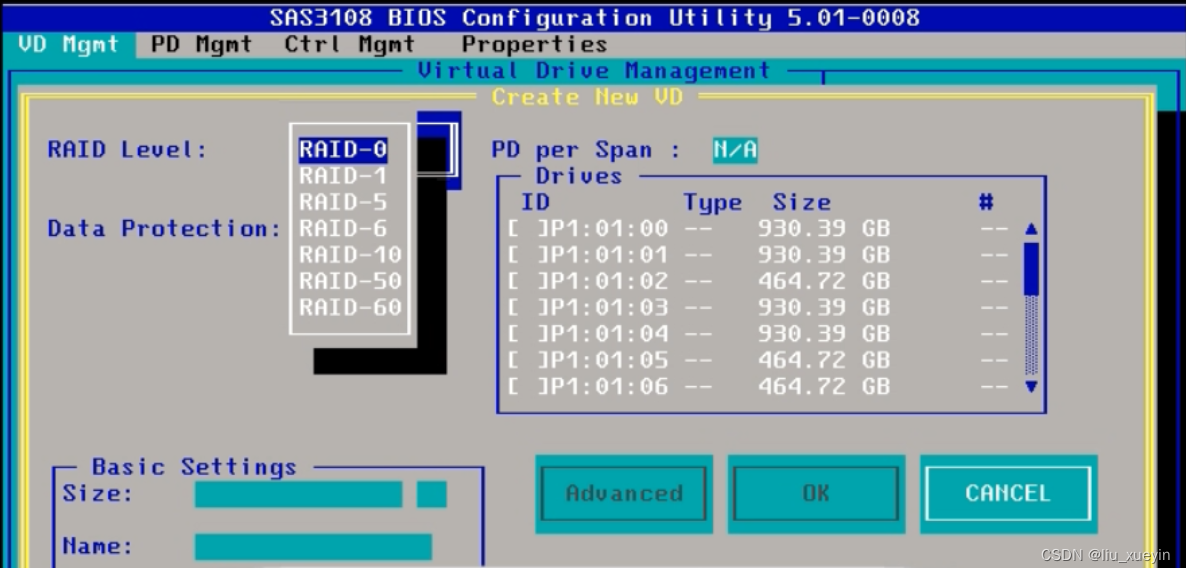
【Linux】服务器与磁盘补充知识,硬raid操作指南
服务器硬件 cpu 主板 内存 硬盘 网卡 电源 raid卡 风扇 远程管理卡 1.硬盘尺寸: 目前生产环境中主流的两种类型硬盘 3.5寸 和2.5寸硬盘 2.5寸硬盘可以通过使用硬盘托架后适用于3.5寸硬盘的服务器 但是3.5寸没法转换成2.5寸 2.如何在服务器上制作raid 华为服务器为例子做…...
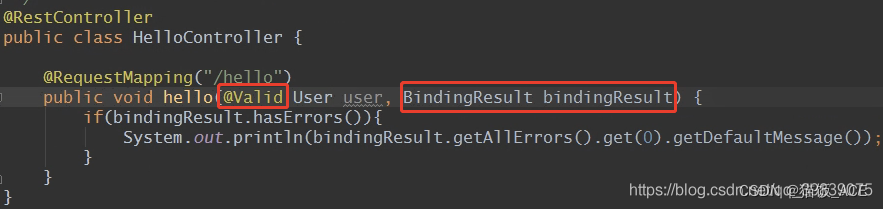
【java】实现自定义注解校验——方法二
自定义注解校验的实现步骤: 1.创建注解类,编写校验注解,即类似NotEmpty注解 2.编写自定义校验的逻辑实体类,编写具体的校验逻辑。(这个类可以实现ConstraintValidator这个接口,让注解用来校验) 3.开启使用自定义注解进…...

算法通关村第六关|白银|二叉树的层次遍历【持续更新】
1.二叉树基本的层序遍历 仅仅遍历并输出全部元素。 List<Integer> simpleLevelOrder(TreeNode root) {if (root null) {return new ArrayList<Integer>();}List<Integer> res new ArrayList<Integer>();LinkedList<TreeNode> queue new Lin…...

vue中通过js控制scss变量
<!--* Description:* Author: 李大玄* Date: 2022-07-28 20:34:43* FilePath: /web-framework-demo/src/views/layout.vue* LastEditors: 李大玄* LastEditTime: 2022-11-01 09:25:31 --> <template><div height"100%" class"b"><inp…...

深度学习理论知识入门【EM算法、VAE算法、GAN算法】和【RBM算法、MCMC算法、HMC算法】
目录 深度学习理论知识入门首先,让我们了解第一个流程:现在,让我们看看第二个流程: EM算法GMM(高斯混合模型) 深度学习理论知识入门 首先,让我们了解第一个流程: EM(Exp…...

Java8实战-总结47
Java8实战-总结47 CompletableFuture:组合式异步编程让代码免受阻塞之苦使用定制的执行器 对多个异步任务进行流水线操作 CompletableFuture:组合式异步编程 让代码免受阻塞之苦 使用定制的执行器 就这个主题而言,明智的选择似乎是创建一个…...

功能: 在web应用程序中、读取文件
通过使用文件 API,web 内容可以要求用户选择本地文件,然后读取这些文件的内容。这种选择可以通过使用 HTML <input type"file"> 元素或通过拖放来完成。 1.通过 click() 方法使用隐藏的文件 input 元素 你可以隐藏公认难看的文件 <…...

TDD、BDD、ATDD以及SBE的概念和区别
在软件开发或是软件测试中会遇到以下这些词:TDD 、BDD 、ATDD以及SBE,这些词代表什么意思呢? 它们之间有什么关系吗? TDD 、BDD 、ATDD以及SBE的基本概念 TDD:(Test Driven Development)是一种…...
Android studio:打开应用程序闪退的问题
目录 问题描述分析原因解决方法 在开发Android应用程序的过程中遇到的问题 问题描述 在开发(或者叫测试,这么简单的程序可能很难叫开发)好一个android之后,在Android studio中调试开发好的app时,编辑器没有提示错误&a…...

Mysql数据库性能优化--performance_SCHEMA.STATEMENTS语句分析
使用performance_schema解决常见的故障案例 1 检查sql语句 使用performance_schema很容易找到引起性能问题的查询以及原因。 要启动语句检测,需要启动statement类型的插装。 插装类: statement/sql sql语句,如select,或者create table。s…...
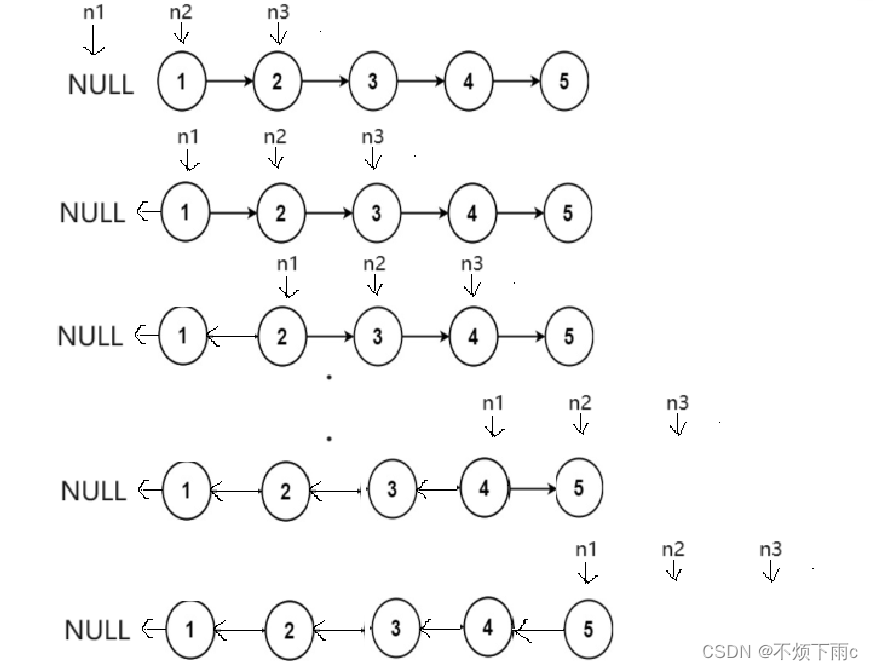
[C/C++]数据结构 链表OJ题: 反转链表
描述: 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表 示例: 方法一: 让链表指向反向 如图所示: 代码思路: struct ListNode* reverseList(struct ListNode* head) {struct ListNode* n1NULL;struct ListNode* n2head;struct ListNode*…...
深度学习之基于YoloV5交通信号标志识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 基于YoloV5交通信号标志识别系统介绍 基于YoloV5的交通信号标志识别系统是一种深度学习应用,旨在通过使…...

Linux命令大全
荒诞也好,愚笨也好,总会过去的 文章目录 文件相关压缩相关tarzip 进程相关pskill 网络相关netstat IPC相关ipcsipcrm 系统资源相关topfreefdiskdfdu 权限相关umaskchmodchownchgrp 总结 文件相关 ls:列出当前目录中的文件和子目录。 ls常用…...
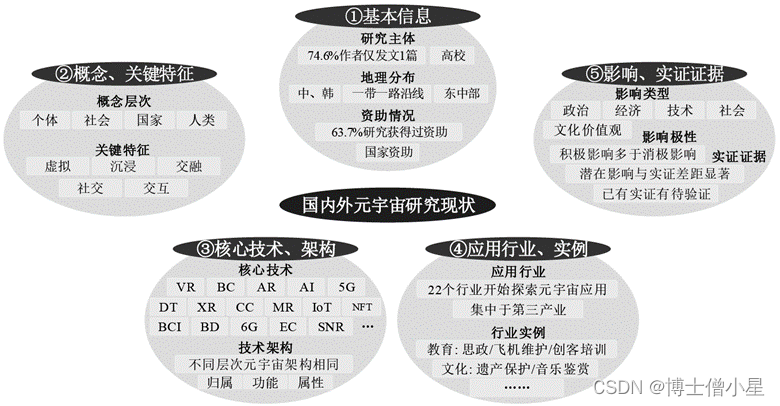
元宇宙是否为噱头?若不是,什么是元宇宙?他的概念、技术、应用和影响是什么?
文章来源:元宇宙的概念、技术、应用与影响——一项系统性文献综述 - 中国知网 (cnki.net) 摘要 [目的/意义]系统综述与分析当前国内外的元宇宙研究现状,有利于准确把握元宇宙发展方向,强化元宇宙基础研究,争取元宇宙建构权。[方法…...

293_C++_告警类
2、IncPos S32 AlarmList::IncPos(U32 *pu32Pos, U32 *pu32Cycle) {if((pu32Pos == NULL) || (pu32Cycle == NULL))</...
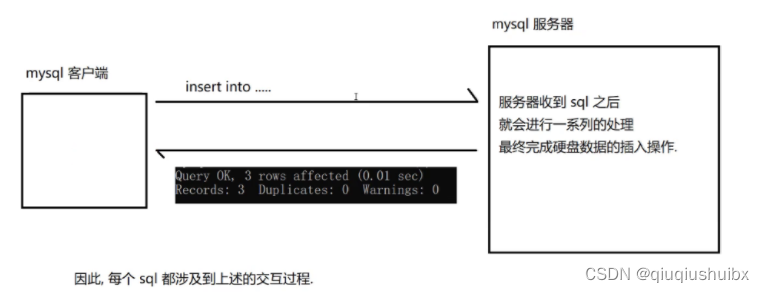
MySQL基础操作
注:mysql是大小写不敏感的. 1.数据库基础操作(展示) //1.展示当前数据库 show databases;//2.创建数据库 create database 数据库名;//3.使用数据库 use 数据库名;//4.删除数据库 drop database 数据库名;2.SQL中基本类型 2.1 数值类型(整数和浮点型) 注:decimal和numeric…...

ajax样式演示
以下是一段Ajax的演示代码,实现了通过Ajax获取后台数据并将其显示到前台页面上。 HTML文件: <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>Ajax演示</title></head><body><h1>学生…...

Web前端—CSS高级(定位、高级技巧、CSS修饰属性、综合案例:购物网站轮播图)
版本说明 当前版本号[20231108]。 版本修改说明20231107初版20231108对知识点(圆点)进行补充 目录 文章目录 版本说明目录day08-CSS高级01-定位相对定位绝对定位定位居中固定定位堆叠层级 z-index定位总结 02-高级技巧CSS精灵案例-京东服务HTML结构CS…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
