【电路笔记】-基尔霍夫电路定律
基尔霍夫电路定律
文章目录
- 基尔霍夫电路定律
- 1、框架和定义
- 2、基尔霍夫电流定律
- 3、基尔霍夫电压定律
- 4、基尔霍夫定律应用
- 5、基尔霍夫定律的局限性
- 6、总结
在本文中,将介绍最基本、最重要的电路定律之一。 这些法律由德国医生古斯塔夫·基尔霍夫 (Gustav Kirchoff) 于 1845 年命名并制定。
与许多物理定律一样,基尔霍夫电路定律 (KCL) 相对容易理解,并且是从能量守恒定律的观察中得出的,这可能是物理学中最古老、最基本的原理之一。
尽管如此,基尔霍夫定律可能简单且易于理解,它们仍然是电路分析中需要掌握的基本工具,并且至今仍被广泛使用。
基尔霍夫定律由与定义电路能量的物理值相关的两个不同定律组成:电流和电压。 下面我们分别分两节介绍基尔霍夫电流定律和电压定律。
在这些部分之前,值得在第一部分中介绍使用 基尔霍夫定律的框架以及与该原则相关的许多定义。
第三部分展示了如何将 基尔霍夫定律应用到实际电路并解决未知参数问题的示例。
最后,最后一节简要介绍了 基尔霍夫定律对于某些特定情况的限制。
1、框架和定义
应用基尔霍夫定律的框架是电路,它由电源或发电机组成,其两个极都与闭环配置中的组件中间连接。 电路根据集总元件模型绘制,该模型假设元件为理想元件,相关表示如下图 1 所示:

我们可以提供一些有关电路拓扑的具体细节。 直线是电路不同元件之间的理想连接/电线,这意味着它们不呈现电阻或电抗行为,因此不存在功率损耗或相移现象。
电源为电路提供电源,电源由电压和电流信号(直流或交流)组成。 这些元件是无源的,它们由电阻器、电容器和电感器的组合组成。 它们可以并联(如图1所示)或串联。 本文将不考虑放大器等有源组件,因为它们与外部电源相关。 用电线连接两端的一组元件称为分支。
为了稍后充分理解基尔霍夫定律,两个重要的拓扑定义非常重要:节点和环。 节点代表分支之间的连接点,它们在图 1 中用蓝色圆圈突出显示。 上图中的红色圆圈箭头突出显示了循环,它表示分支的闭合路径。
2、基尔霍夫电流定律
电流定律也称为节点定律或结定律,规定在节点处相遇的电流的代数和等于零。 可以用连接三个分支的节点来说明一个简单的示例:

因此,该定律规定进入节点的电流总和等于离开结点的电流。 在我们的示例中,这句话在数学上翻译为 I 1 + I 2 = I 3 I_1+I_2=I_3 I1+I2=I3 或 I 1 + I 2 − I 3 = 0 I_1+I_2-I_3=0 I1+I2−I3=0,当前 I 3 I_3 I3 为负,因为它正在退出节点。
一般情况下,N 个支路的节点结点的电流标记为 I 1 、 I 2 、 … 、 I N I_1、I_2、…、I_N I1、I2、…、IN 满足以下方程 1:

如果当前 I k I_k Ik 进入节点,则符号函数 s g n sgn sgn 等于 +1;如果存在,则符号函数 s g n sgn sgn 等于 -1。
节点定律是根据封闭系统中电荷不变的观察直接写出的。 该假设也称为电荷守恒定律。
在物理学中,原理是指没有经验证明无效但尚未被证明的观察结果,相当于数学中的假设。
3、基尔霍夫电压定律
电压定律也称为环路规则,它与节点规则非常相似,但适用于环路而不是节点。 第二定律指出电路环路中电压的代数和为零。 可以用为串联 RC 滤波器供电的直流电源来说明一个简单的示例:

电压的符号由箭头的方向决定,通常认为源为正,因此顺时针箭头为正,逆时针箭头为负。 因此,基尔霍夫电压定律规定 V S = V R + V C V_S=V_R+V_C VS=VR+VC 或 V S − V R − V C = 0 V_S-V_R-V_C=0 VS−VR−VC=0。
对于具有 N 个电压 V 1 、 V 2 、 … 、 V N V_1、V_2、…、V_N V1、V2、…、VN 生成和下降的环路,满足公式2:

当产生电压(我们示例中的源)时,符号函数 sgn 等于 +1;当观察到电压下降时(使用图 3 中的无源组件),符号函数 sgn 等于 -1。
4、基尔霍夫定律应用
在本节中,我们将展示使用 KCL 可以解决的典型问题的解决过程。 如下图 4 所示配置中与电阻器 R 1 R_1 R1、 R 2 R_2 R2 和 R 3 R_3 R3 连接的三个电源 S 1 S_1 S1、 S 2 S_2 S2 和 S 3 S_3 S3:

电源是直流且理想的,这意味着它们不存在内阻。 我们取 S 1 = 4 V S_1=4V S1=4V, S 2 = 3 V S_2=3V S2=3V, S 3 = 10 V S_3=10V S3=10V, R 1 = 3 Ω R_1=3\Omega R1=3Ω, R 2 = 2 Ω R_2=2\Omega R2=2Ω, R 3 = 1 Ω R_3=1\Omega R3=1Ω。
根据基尔霍夫电流定律,我们可以为节点 1 和 2 写出以下等式:
- 节点1: I 1 = I 2 + I 3 I_1=I_2+I_3 I1=I2+I3
- 节点2: I 2 + I 3 = I 1 I_2+I_3=I_1 I2+I3=I1,与节点1的方程类似
根据基尔霍夫电压定律,我们写出Loop 1 和Loop 2 的等式:
- Loop1: S 1 = S 2 + R 2 × I 2 + R 1 × I 1 S_1=S_2+R_2×I_2+R_1×I_1 S1=S2+R2×I2+R1×I1
- Loop2: S 2 + R 2 × I 2 = S 3 + R 3 × I 3 S_2+R_2×I_2=S_3+R_3×I_3 S2+R2×I2=S3+R3×I3
我们可以以不同的方式编写这些方程,以获得以下具有 3 个未知参数 I 1 I_1 I1、 I 2 I_2 I2 和 I 3 I_3 I3 的 3 个方程组:

该系统可以用消除法求解,即在第二行( L 2 L_2 L2)中将 I 1 I_1 I1 替换为 I 2 + I 3 I_2+I_3 I2+I3,并通过加法 R 3 × L 2 + R 1 × L 3 R_3×L_2+R_1×L_3 R3×L2+R1×L3 消除项 I 3 I_3 I3。
我们直接找到 I 2 = 4.2 A I_2=4.2A I2=4.2A,然后我们可以通过替换 L 3 L_3 L3中的 I 2 I_2 I2来找到 I 3 I_3 I3,得到 I 3 = 1.4 A I_3=1.4A I3=1.4A,最后我们得到 I 1 = I 2 + I 3 = 5.6 A I_1=I_2+I_3=5.6A I1=I2+I3=5.6A。
5、基尔霍夫定律的局限性
在第一部分中,我们已经了解了 KCL 应用的框架,但电路还必须遵守一些其他更微妙的条件。 我们在本节中简要强调了 KCL 有效的进一步条件。
第一个条件称为准静态近似(The Quasistatic Approximation),即信号的传播时间与信号的周期相比必须可以忽略不计,这给出了电路尺寸的条件。
例如,考虑 200 k H z ( T = 5 μ s ) 200 kHz (T=5 \mu s) 200kHz(T=5μs)的交流信号,如果接收器位于电路中 D = 10 c m D=10cm D=10cm 处,则传播时间将为 △ t = D / c = 0.33 n s \triangle t=D/c=0.33 ns △t=D/c=0.33ns,其中 c c c 为 光速。 在这种情况下, △ t < < T \triangle t<<T △t<<T,准静态近似有效并且遵守应用 KCL 的条件。
然而,如果接收器位于 D = 1 k m D=1 km D=1km,则传播时间变为 △ t = 3.3 μ s \triangle t=3.3 \mu s △t=3.3μs,并且不遵守不等式 △ t < < T \triangle t<<T △t<<T,因此近似无效,并且 KCL 无法应用于电路。
在准静态近似中,源的任何变化都被认为会立即传播到电路中的任何点,从而避免了可能使 KCL 失效的延迟效应。
这个可以用**麦克斯韦-安培方程(Maxwell-Ampere)来证明,其中当准静态近似有效时可以消除变分项,然后可以用格林-奥斯特罗格拉茨基定理(Green-Ostrogradski)**来证明基尔霍夫电流定律。
赋予 KCL 有效性的另一个常见条件是电路回路上的磁通量的变化必须可以忽略不计。 根据感应定律,磁通量的变化会在电路中产生感应电流,从而产生感应电压。
磁通的变化引入了一个新的电压项,该电压项不是由元件或电路的拓扑结构解释的,而是来自外部源,从而使环路规则失效。
6、总结
- 基尔霍夫定律是电子学的基本定律,可应用于由环路和节点构成的电路。 这些拓扑定义以及其他拓扑定义在本文的第一部分中介绍,该部分提供了应用 基尔霍夫定律的框架。
- 基尔霍夫定律由电流定律和电压定律组成,反映了电路中能量守恒定律。
- 电流定律考虑了电荷守恒,它指出节点中电流的代数和等于零。 电压定律规定环路中电压的代数和为零。
- 接下来的章节介绍了使用这两个定律可以通过求解线性方程组来解决典型的电子问题。
- 最后,我们在最后一节中简要介绍了为了使 基尔霍夫定律有效,必须考虑有关电路尺寸和外部磁通量存在的一些微妙条件。
相关文章:

【电路笔记】-基尔霍夫电路定律
基尔霍夫电路定律 文章目录 基尔霍夫电路定律1、框架和定义2、基尔霍夫电流定律3、基尔霍夫电压定律4、基尔霍夫定律应用5、基尔霍夫定律的局限性6、总结 在本文中,将介绍最基本、最重要的电路定律之一。 这些法律由德国医生古斯塔夫基尔霍夫 (Gustav Kirchoff) 于 …...

从零开始搭建React+TypeScript+webpack开发环境-基于axios的Ajax请求工具
什么是axios axios是一款基于Promise的HTTP客户端,适用于浏览器和Node.js环境。它的特点包括: 支持浏览器和Node.js环境。支持Promise API。支持拦截请求和响应。支持取消请求。自动转换JSON数据。支持CSRF保护。 使用axios可以更方便地发送HTTP请求&…...
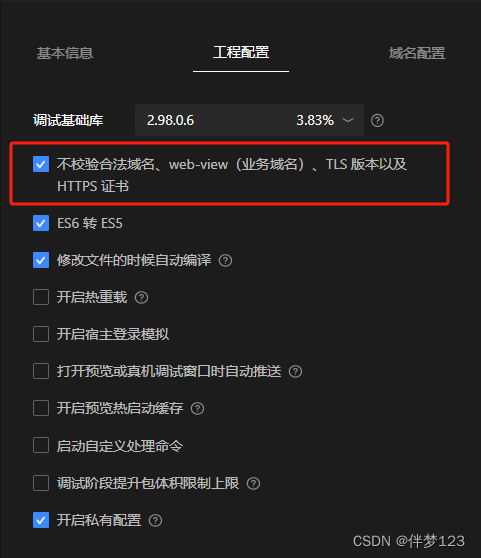
【uniapp小程序下载】调用uni.uploadfile方法在调试工具里是没有问题的,但是线上版本和体验版就调用不成功,真机调试也没问题
把你的下载地址前缀添加到合法域名就解决了 在调试工具里成功了是因为勾选了下面这项 下面是我的下载并打开函数 methods: {// 下载downloadFileFn(data) {if (this.detailsObj.currentUserBuy) {uni.downloadFile({// data是路径url: https:// data,success(res) {//保存到本…...

chatGLM中GLM设计思路
GLM是结合了MLM和CLM的一种预训练方式,其中G为general;在GLM中,它不在以某个token为粒度,而是一个span(多个token),这些span之间使用自编码方式,而在span内部的token使用自回归的方式…...

卡牌游戏类型定制开发微信卡牌小程序游戏
卡牌类型的游戏开发具有一些独特的特点和挑战,以下是一些主要的特点: 卡牌设计和平衡:卡牌游戏的核心是卡牌设计和平衡。开发团队需要设计各种卡牌,确保它们在游戏中相互平衡,以便提供有趣的游戏体验。卡牌的特性、效…...

web —— css(1)
Web —— css基础 1. CSS样式表2. CSS的三种引入方式3. CSS 语法4. CSS 选择器4.1 元素选择器4.2 类选择器4.3 ID选择器4.4 属性选择器4.5 后代选择器4.6 子元素选择器4.7 伪类选择器4.8 分组选择器 5. 颜色和字体6. 显示方式display7. 盒子模型7.1 盒子模型 - 外边距塌陷7.2 盒…...

站群服务器的特性和好处是什么
站群服务器的特性和好处是什么 站群服务器的特性是什么?站群服务器是一种为一个网站或多个网站配置独立IP的服务器。因而相比一般的服务器,站群服务器最大的特性就是IP数量是非常的多。那么租用站群服务器使用有什么好处呢? 多网站优化 大…...

竞赛 行人重识别(person reid) - 机器视觉 深度学习 opencv python
文章目录 0 前言1 技术背景2 技术介绍3 重识别技术实现3.1 数据集3.2 Person REID3.2.1 算法原理3.2.2 算法流程图 4 实现效果5 部分代码6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习行人重识别(person reid)系统 该项目…...

软件设计模式的意义
软件设计模式的意义 所有开发人员都应该接触过软件设计模式这个概念,看过《设计模式-可复用的对象软件的基础》这本书,在面试中都被问过: 你用过哪些设计模式这种问题。但很大可能也就仅此而已了。 为什么好像只能从框架中找到设计模式的应用…...
vue基础知识十八:说说你对keep-alive的理解是什么?
一、Keep-alive 是什么 keep-alive是vue中的内置组件,能在组件切换过程中将状态保留在内存中,防止重复渲染DOM keep-alive 包裹动态组件时,会缓存不活动的组件实例,而不是销毁它们 keep-alive可以设置以下props属性:…...
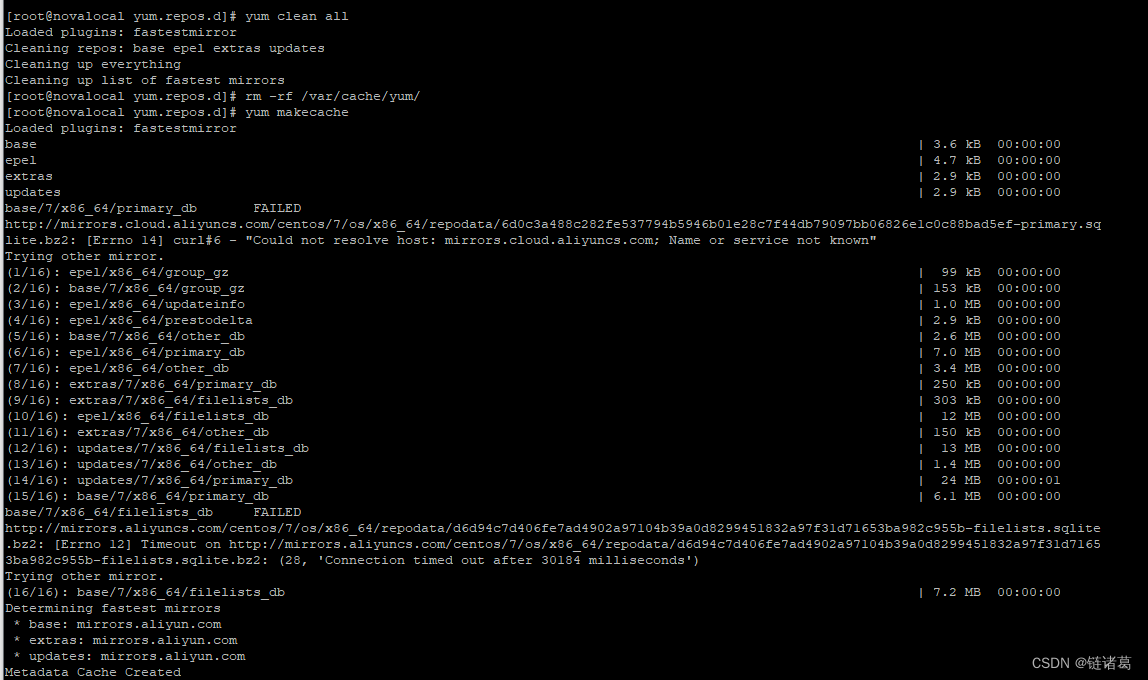
Linux CentOS配置阿里云yum源
一:先备份文件,在配置失败时可以恢复 cd /etc/yum.repos.d mkdir back mv *.repo back 二:下载阿里云yum源 wget -O /etc/yum.repos.d/CentOS-Base.repo https://mirrors.aliyun.com/repo/Centos-7.repo wget -O /etc/yum.repos.d/epel…...

ESP32网络开发实例-Web服务器以仪表形式显示传感器计数
Web服务器以仪表形式显示传感器计数 文章目录 Web服务器以仪表形式显示传感器计数1、应用介绍2、软件准备3、硬件准备4、代码实现4.1 Web页面文件4.2 Web服务器代码实现在本文中,我们将介绍使用服务器发送事件 (SSE) 构建 ESP32 仪表 Web 服务器。服务器将自动向所有连接的网络…...

@Bean有哪些属性
直接看原文 原文链接:Spring中bean标签的作用和属性的详解-CSDN博客 -------------------------------------------------------------------------------------------------------------------------------- Bean的配置一般都在XML文件进行配置Bean相关包为:or…...

【Qt之绘制兔纸】
效果 代码 class drawRabbit: public QWidget { public:drawRabbit(QWidget *parent nullptr) : QWidget(parent) {}private:void paintEvent(QPaintEvent *event) {QPainter painter(this);painter.setRenderHint(QPainter::Antialiasing, true);// 绘制兔子的耳朵painter.s…...
JS+CSS随机点名详细介绍复制可用(可自己添加人名)
想必大家也想拥有一个可以随机点名的网页,接下来我为大家介绍一下随机点名,可用于抽人,哈哈 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title><style>* {margin: 0;…...

西瓜书笔记
周志华老师亲讲-西瓜书全网最详尽讲解-1080p高清原版《机器学习初步》 周志华机器学习(西瓜书)学习笔记(持续更新) 周志华《Machine Learning》学习笔记 绪论 基本术语 数据集(data set):一堆…...

学算法常用刷题网站
学算法常用刷题网站 AcWing : 北大报送生,NOI金牌得主—yxc创办 CodeForces: 简称CF,俄罗斯的网站 hduoj: 杭州电子科技大学的在线评测系统 vjudge:用户可以自己举办比赛 POJ: 北京大学的在线评测系统 洛谷:很火的刷题网站 计蒜客…...
-37)
hdlbits系列verilog解答(always块条件语句)-37
文章目录 一、问题描述二、verilog源码三、仿真结果一、问题描述 Verilog 有一个三元条件运算符 ( ? : ) 很像 C语言: (condition ? if_true : if_false) 这可用于根据一行上的条件(多路复用器!)选择两个值之一,而无需在组合 always 块中使用 if-then。 举例: (0…...

智能井盖生产商家,万宾科技井盖传感器产品详情
市政府管理水平决定城市人民幸福程度,所以在智慧城市推进过程中,市政府也在加快城市信息基础设施建设,希望提高公共服务水平,以此来满足城市居民的需求,进一步推进城市信息化智能化发展。作为城市生命线的一个组成部分…...
开启AWS的ubuntu服务器的root用户登录权限
设置root用户密码 输入以下命令修改root用户密码 sudo passwd root输入以下命令切换到root用户 su root仅允许root用户用密码登录 输入以下命令编辑ssh配置文件 vi /etc/ssh/sshd_config新增以下配置允许root用户登录 PermitRootLogin yes把PasswordAuthentication修改为…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
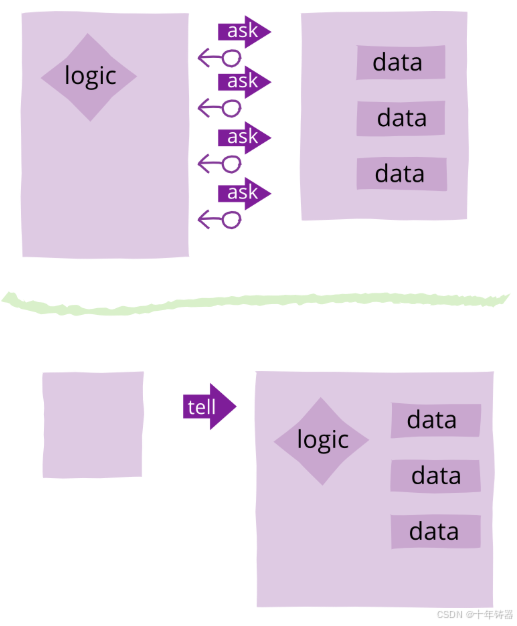
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...

使用VMware克隆功能快速搭建集群
自己搭建的虚拟机,后续不管是学习java还是大数据,都需要集群,java需要分布式的微服务,大数据Hadoop的计算集群,如果从头开始搭建虚拟机会比较费时费力,这里分享一下如何使用克隆功能快速搭建一个集群 先把…...

【图片转AR场景】Tripo + Blender + Kivicube 实现图片转 AR 建模
总览 1.将 2D 图片转为立体建模 2. 3. 一、将 2D 图片转为立体建模 1.工具介绍 Tripo 网站 2.找图片 找的图片必须是看起来能够让 AI 有能力识别和推理的,因为现在的AI虽然可以补全但是能力还没有像人的想象力那么丰富。 比如上面这张图片,看起来虽…...

spring中的@KafkaListener 注解详解
KafkaListener 是 Spring Kafka 提供的一个核心注解,用于标记一个方法作为 Kafka 消息的消费者。下面是对该注解的详细解析: 基本用法 KafkaListener(topics "myTopic", groupId "myGroup") public void listen(String message)…...
