LeetCode----149. 直线上最多的点数
题目
给你一个数组 points ,其中 points[i] = [ x i x_i xi, y i y_i yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
示例 1:
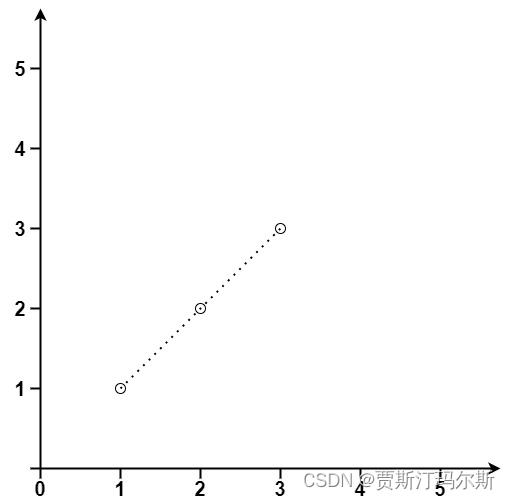
输入:points = [[1,1],[2,2],[3,3]]
输出:3
示例 2:
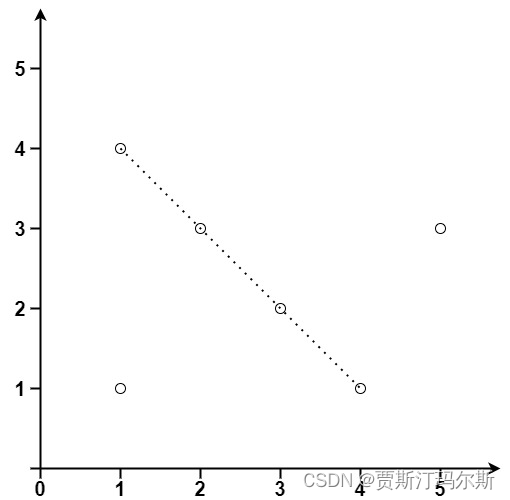
输入:points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出:4
提示:
1 <= points.length <= 300
points[i].length == 2
-104 <= xi, yi <= 1 0 4 10^4 104
points 中的所有点 互不相同
解
解决这个问题的常用方法是使用哈希表。对于给定的点 ( x i x_i xi, y i y_i yi),我们可以计算其与其他点的斜率 ( x j x_j xj - x i x_i xi) / ( y j y_j yj - y i y_i yi),并将这个斜率存储在哈希表中。
具体步骤如下:
- 遍历每一个点 ( x i x_i xi, y i y_i yi),对于每个点,初始化一个哈希表 slopeMap,用于存储以该点为起点的直线上的点数。
- 然后再次遍历每一个点 ( x j x_j xj, y j y_j yj)(这个循环将计算所有点与点 ( x i x_i xi, y i y_i yi) 的斜率),如果 ( x j x_j xj, y j y_j yj) 与 ( x i x_i xi, y i y_i yi) 重合,将 overlap 值加 1,否则计算斜率 ( x j x_j xj - x i x_i xi) / ( y j y_j yj - y i y_i yi)。
- 将计算得到的斜率存储在 slopeMap 中,如果已存在该斜率,直线上的点数加 1,如果不存在,则初始化为 2(包括 ( x i x_i xi, y i y_i yi) 和 ( x j x_j xj, y j y_j yj))。
- 在每次内循环结束后,更新 maxPoints,确保始终保持记录最多点的直线上的点数。
- 继续遍历下一个点 ( x i x_i xi, y i y_i yi),并重复上述过程,直到所有点都被处理。
以下是Java代码示例:
class Solution {public int maxPoints(int[][] points) {if (points.length < 3) {return points.length;}int maxPoints = 2; // 初始化最大点数为2,因为至少有两个点在同一直线上for (int i = 0; i < points.length; i++) {int overlap = 0; // 用于记录与当前点重合的点数HashMap<Double, Integer> slopeMap = new HashMap<>(); // 用于存储斜率与点数的映射for (int j = 0; j < points.length; j++) {if (i == j) {overlap++; // 与自身重合的点数加1} else {double slope;if (points[i][0] == points[j][0]) {slope = Double.POSITIVE_INFINITY; // 当x坐标相同时,斜率设为正无穷大} else {slope = (double)(points[i][1] - points[j][1]) / (points[i][0] - points[j][0]); // 计算斜率}slopeMap.put(slope, slopeMap.getOrDefault(slope, 0) + 1); // 存储斜率并更新点数}}int localMax = overlap; // 初始化局部最大点数为与自身重合的点数for (int count : slopeMap.values()) {localMax = Math.max(localMax, count + overlap); // 更新局部最大点数}maxPoints = Math.max(maxPoints, localMax); // 更新全局最大点数}return maxPoints;}
}
这段代码通过哈希表来统计每个点的斜率,然后记录直线上的点数,最终找到直线上点数最多的情况。
解2
除了上述的哈希表解法外,还有一种更优化的解法,可以在O(n^2)的时间内解决问题,其中n是点的数量。
这个解法基于以下观察:如果有三个点共线,那么它们的斜率是相同的。因此,我们可以遍历每一对点,计算它们之间的斜率,并存储在哈希表中。对于每个点,我们统计共线的点的数量,并保持更新最大值。
以下是基于这种观察的Java代码:
class Solution {public int maxPoints(int[][] points) {if (points.length < 3) {return points.length;}int maxPoints = 2; // 初始化最大点数为2,因为至少有两个点在同一直线上for (int i = 0; i < points.length; i++) {int overlap = 0; // 用于记录与当前点重合的点数HashMap<String, Integer> slopeMap = new HashMap<>(); // 用于存储斜率与点数的映射for (int j = 0; j < points.length; j++) {if (i == j) {overlap++; // 与自身重合的点数加1} else {int deltaX = points[i][0] - points[j][0];int deltaY = points[i][1] - points[j][1];if (deltaX == 0) {slopeMap.put("inf", slopeMap.getOrDefault("inf", 0) + 1); // 斜率为正无穷} else {int gcd = gcd(deltaX, deltaY);String slope = (deltaY / gcd) + "/" + (deltaX / gcd); // 用字符串表示斜率slopeMap.put(slope, slopeMap.getOrDefault(slope, 0) + 1);}}}int localMax = overlap; // 初始化局部最大点数为与自身重合的点数for (int count : slopeMap.values()) {localMax = Math.max(localMax, count + overlap); // 更新局部最大点数}maxPoints = Math.max(maxPoints, localMax); // 更新全局最大点数}return maxPoints;}// 辗转相除法计算最大公约数private int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);}
}
这种解法避免了使用浮点数斜率,使用最大公约数来保持斜率的精度,同时也处理了斜率为正无穷的情况。这个解法的时间复杂度为O(n^2),但在实际应用中通常更高效。
解3
动态规划的思路是,对于每个点 (xi, yi),可以考虑以它为终点的直线上的点数,然后记录最大值。下面是一个使用动态规划的Java代码示例:
class Solution {public int maxPoints(int[][] points) {if (points.length < 3) {return points.length;}int maxPoints = 2; // 初始化最大点数为2,因为至少有两个点在同一直线上int n = points.length;for (int i = 0; i < n; i++) {int overlap = 0; // 用于记录与当前点重合的点数int localMax = 0; // 用于记录以当前点为终点的直线上的点数HashMap<String, Integer> slopeMap = new HashMap<>(); // 用于存储斜率与点数的映射for (int j = i + 1; j < n; j++) {int deltaX = points[i][0] - points[j][0];int deltaY = points[i][1] - points[j][1];if (deltaX == 0 && deltaY == 0) {overlap++; // 与自身重合的点数加1} else {int gcd = gcd(deltaX, deltaY);String slope = (deltaY / gcd) + "/" + (deltaX / gcd); // 用字符串表示斜率slopeMap.put(slope, slopeMap.getOrDefault(slope, 0) + 1); // 存储斜率并更新点数localMax = Math.max(localMax, slopeMap.get(slope)); // 更新以当前点为终点的直线上的点数}}maxPoints = Math.max(maxPoints, localMax + overlap + 1); // 更新全局最大点数,加1是因为还包括自身点}return maxPoints;}// 辗转相除法计算最大公约数private int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);}
}
相关文章:

LeetCode----149. 直线上最多的点数
题目 给你一个数组 points ,其中 points[i] [ x i x_i xi, y i y_i yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。 示例 1: 输入:points [[1,1],[2,2],[3,3]] 输出:3 示例 2: 输入…...
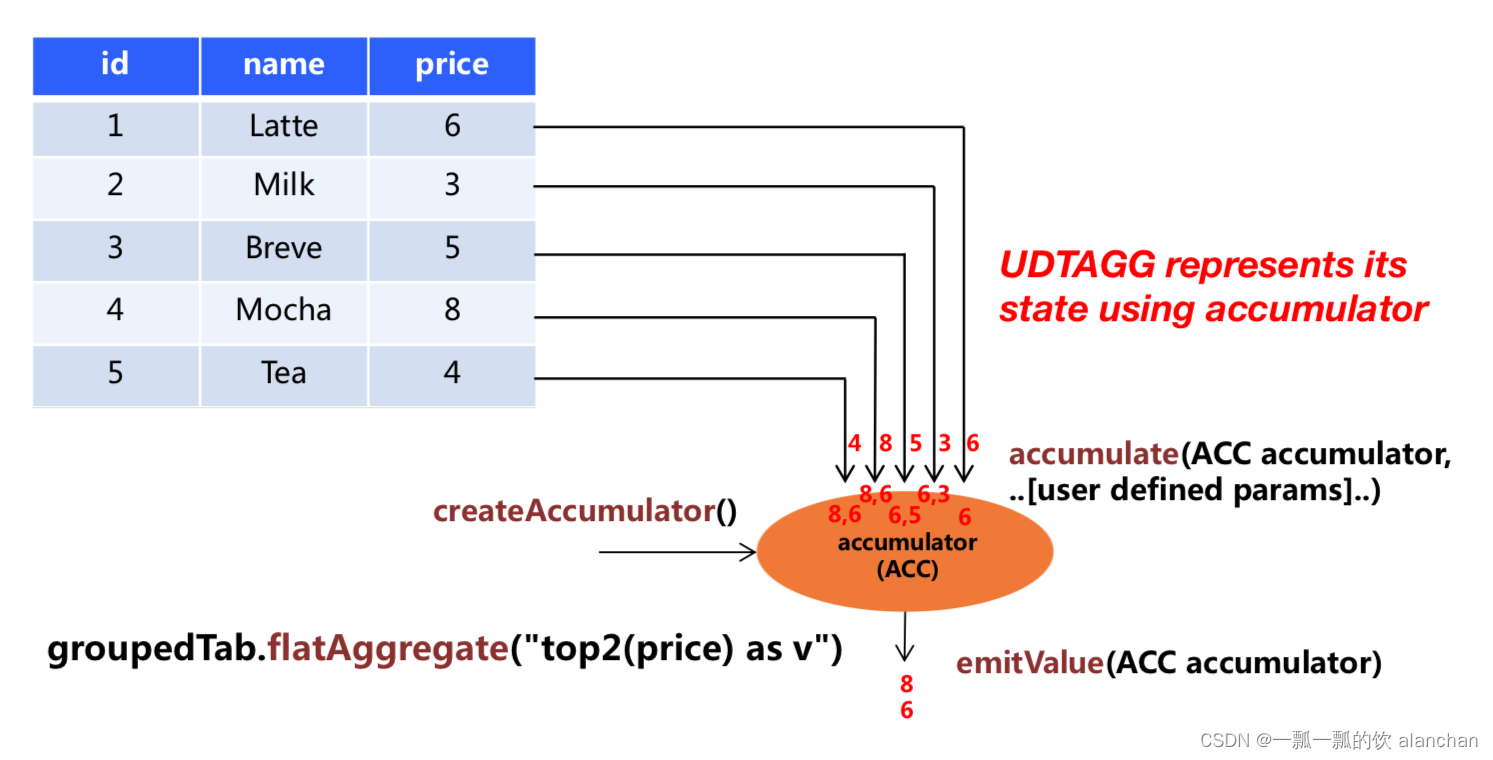
19、Flink 的Table API 和 SQL 中的自定义函数及示例(3)
Flink 系列文章 1、Flink 部署、概念介绍、source、transformation、sink使用示例、四大基石介绍和示例等系列综合文章链接 13、Flink 的table api与sql的基本概念、通用api介绍及入门示例 14、Flink 的table api与sql之数据类型: 内置数据类型以及它们的属性 15、Flink 的ta…...

Flutter IOS 前后台切换主题自动变化的问题
BUG 触发条件 设备 IOS 15 模拟器GetX 实现换肤GetMaterialApp 里面配置好 theme和darkTheme使用GetView和GetController进行开发 此时如果把App前后台切换,使用Obx包括起来的内容会跟谁异常主题变换,未使用Obx的颜色不会变化。 解决路径 首先在获取 …...
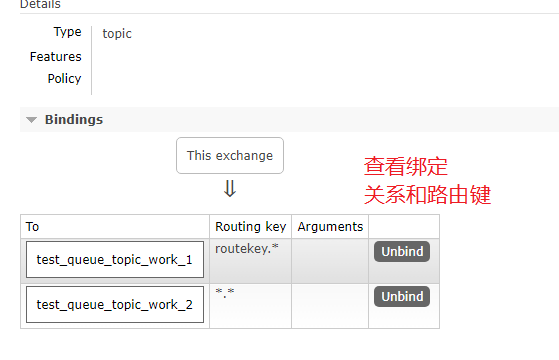
rabbitmq入门学习
写在前面 本文看下rabbit mq的基础概念以及使用。 1:简单介绍 为了不同进程间通信的解耦,出现了消息队列,为了规范消息队列的具体实现,Java制定了jms规范,这是一套基于接口的规范,因此是绑定语言的&…...
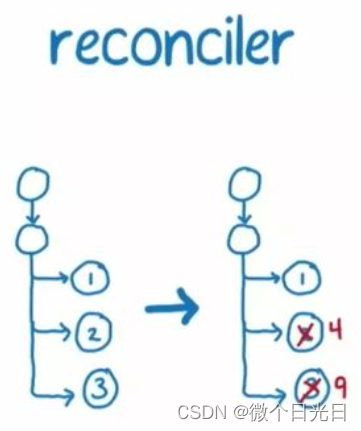
说说对Fiber架构的理解?解决了什么问题?
一、问题 JavaScript引擎和页面渲染引擎两个线程是互斥的,当其中一个线程执行时,另一个线程只能挂起等待 如果 JavaScript 线程长时间地占用了主线程,那么渲染层面的更新就不得不长时间地等待,界面长时间不更新,会导…...
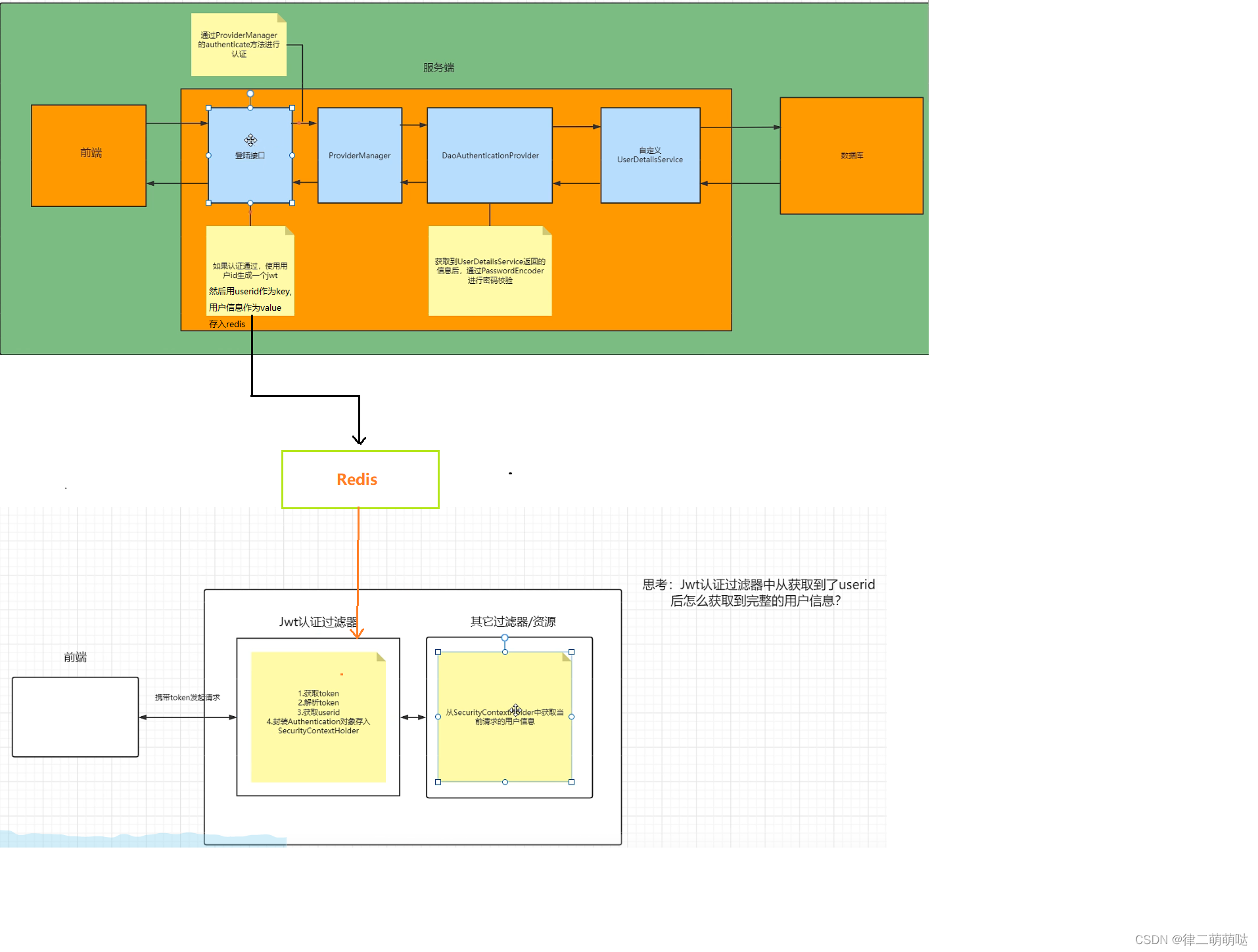
Spring Security笔记
Spring Security 是 Spring家族中的一个安全管理框架。 一般来说中大型的项目都是使用 SpringSecurity 来做安全框架,小项目用相对简单的Shiro。认证、授权是 SpringSecurity 作为安全框架的核心功能。 认证:通过用户名密码验证当前访问系统的是不是本…...
快速教程|如何在 AWS EC2上使用 Walrus 部署 GitLab
Walrus 是一款基于平台工程理念的开源应用管理平台,致力于解决应用交付领域的深切痛点。借助 Walrus 将云原生的能力和最佳实践扩展到非容器化环境,并支持任意应用形态统一编排部署,降低使用基础设施的复杂度,为研发和运维团队提供…...
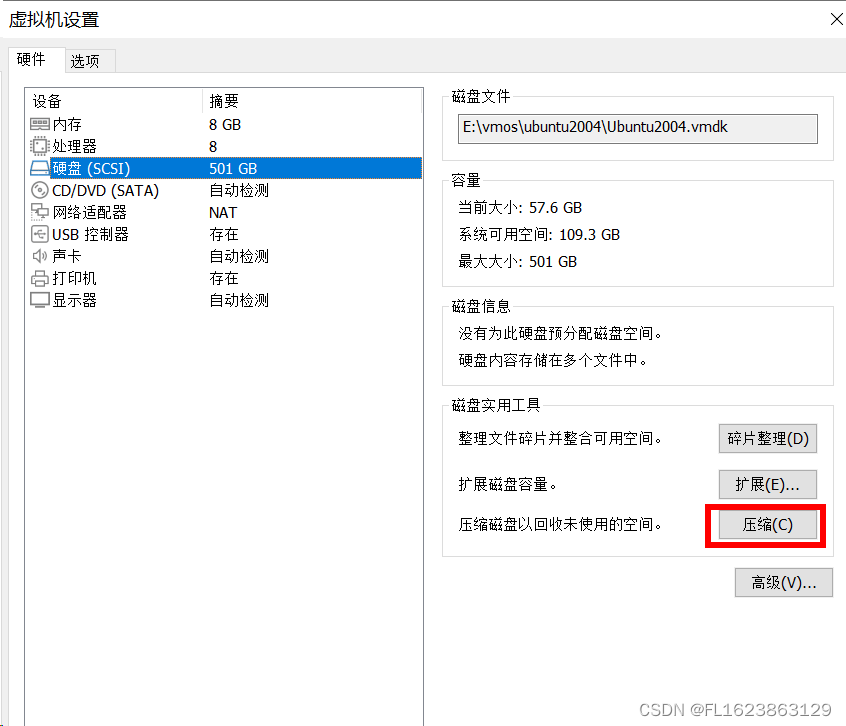
[vmware]vmware虚拟机压缩空间清理空间
vmware中的ubuntu使用如果拷贝文件进去在删除,vmare镜像文件并不会减少日积月累会不断是的真实物理磁盘空间大幅度减少,比如我以前windows操作系统本来只有30GB最后居然占道硬盘200GB,清理方法有2种。 第一种:vmware界面操作 第二…...

一篇文章带你使用(MMKV--基于 mmap 的高性能通用 key-value 组件)
一、MMKV是什么? MMKV 是基于 mmap 内存映射的 key-value 组件,底层序列化/反序列化使用 protobuf 实现,性能高,稳定性强。也是腾讯微信团队使用的技术。 支持的数据类型 支持以下 Java 语言基础类型: boolean、int…...
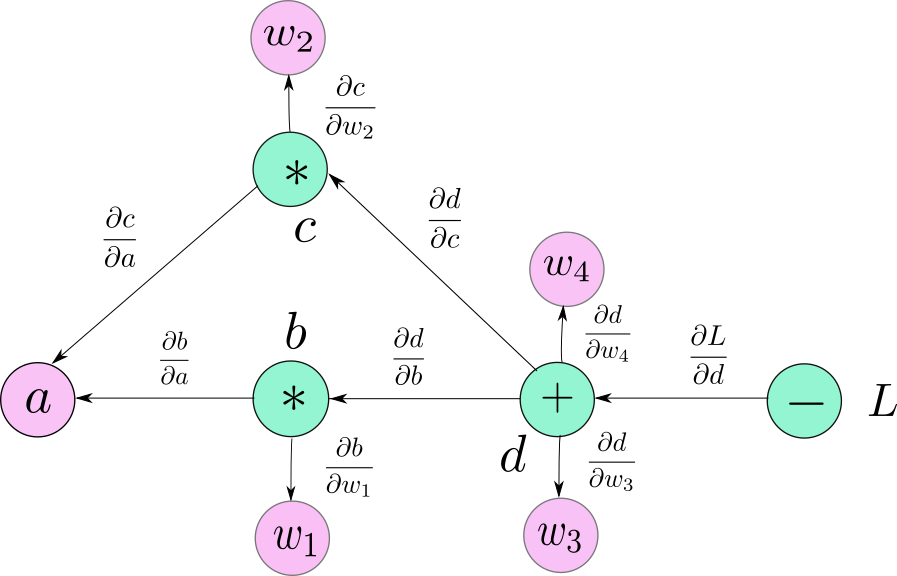
Pytorch 里面torch.no_grad 和model.eval(), model.train() 的作用
torch.no_grad: 影响模型的自微分器,使得其停止工作;这样的话,数据计算的数据就会变快,内存占用也会变小,因为没有了反向梯度计算,当然,我哦们也无法做反向传播。 model.eval() 和model.train()…...
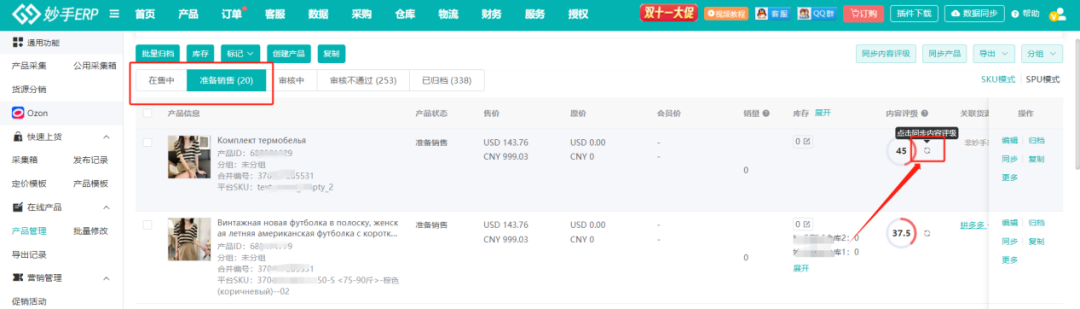
Ozon产品内容评级功能上线,妙手ERP实力助力Ozon卖家全方位打造爆款产品!
产品内容评级,可以直接反映产品质量的高低,也是影响产品排名的关键。具有较高内容评级的产品,将有更大机会显示在搜索结果和类目的前几页中,从而引起买家的关注,促进销售。 为帮助卖家打造高质量产品,妙手…...

Linux 下最主流的文件系统格式——ext
硬盘分成相同大小的单元,我们称为块(Block)。一块的大小是扇区大小的整数倍,默认是 4K。在格式化的时候,这个值是可以设定的。 一大块硬盘被分成了一个个小的块,用来存放文件的数据部分。这样一来…...
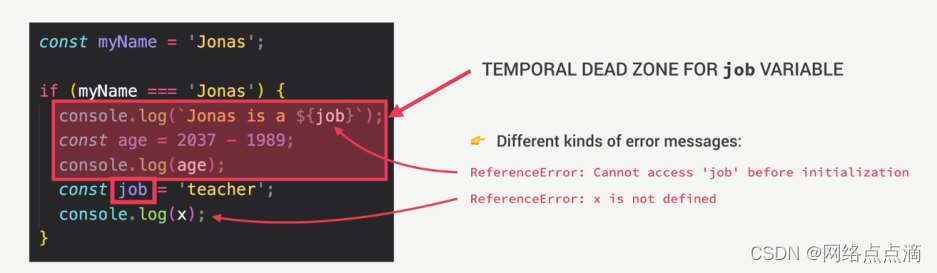
变量环境、变量提升和暂时性死区
JavaScript中的提升 在JavaScript中,“Hoisting”(提升)是一种特性,它将变量和函数的声明移动到作用域的顶部。这意味着可以在声明之前使用这些变量和函数,而不会报错。 当JavaScript代码执行时,会经过两个…...

yolov8+多算法多目标追踪+实例分割+目标检测+姿态估计(代码+教程)
多目标追踪实例分割目标检测 YOLO (You Only Look Once) 是一个流行的目标检测算法,它能够在图像中准确地定位和识别多个物体。 本项目是基于 YOLO 算法的目标跟踪系统,它将 YOLO 的目标检测功能与目标跟踪技术相结合,实现了实时的多目标跟…...
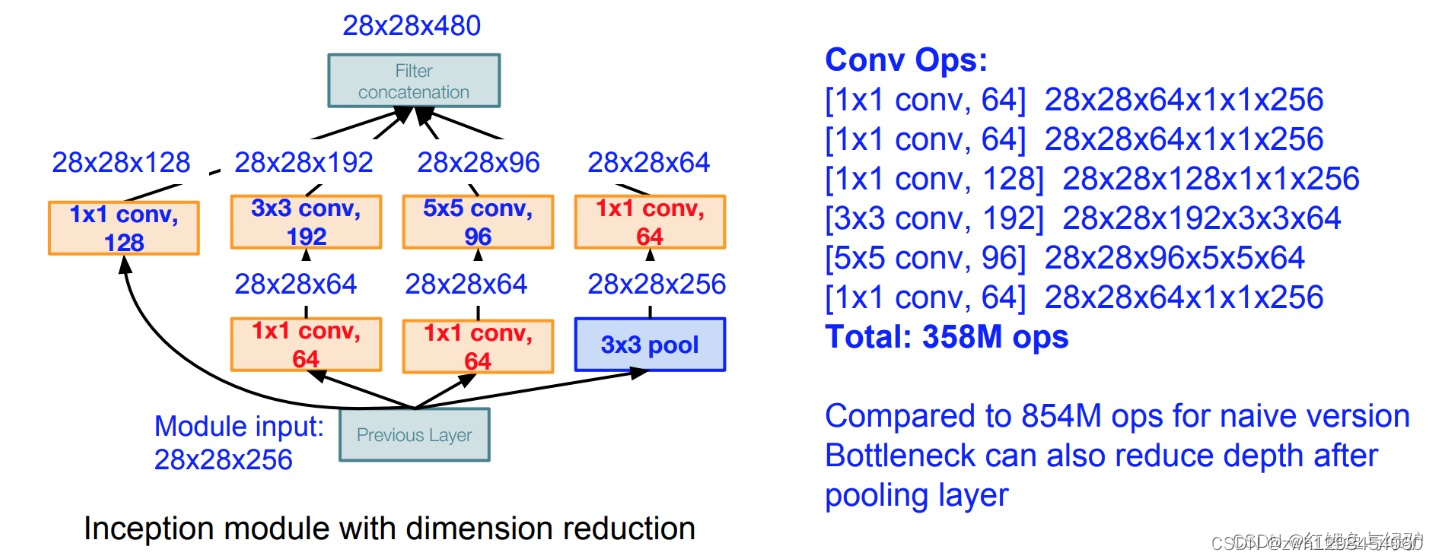
【神经网络】【GoogleNet】
1、引言 卷积神经网络是当前最热门的技术,我想深入地学习这门技术,从他的发展历史开始,了解神经网络算法的兴衰起伏;同时了解他在发展过程中的**里程碑式算法**,能更好的把握神经网络发展的未来趋势,了解神…...
网络安全深入学习第八课——正向代理(工具:ReGeorg)
文章目录 一、环境配置二、开始模拟1、拿下跳板机的Webshell权限,并上传shell文件1.1、查看跳板机网络环境1.2、查看arp表 2、使用ReGeorg来建立连接2.1、生产ReGeorg隧道文件2.2、上传ReGeorg隧道的PHP脚本到跳板机2.3、连接隧道2.4、尝试浏览器连接 3、使用Proxif…...
Jmeter全流程性能测试实战
项目背景: 我们的平台为全国某行业监控平台,经过3轮功能测试、接口测试后,98%的问题已经关闭,决定对省平台向全国平台上传数据的接口进行性能测试。 01、测试步骤 1、编写性能测试方案 由于我是刚进入此项目组不久,…...
Python算法例8 将整数A转换为B
1. 问题描述 给定整数A和B,求出将整数A转换为B,需要改变bit的位数。 2. 问题示例 把31转换为14,需要改变2个bit位,即:(31)10(11111)2,(14&…...

一个基于百度飞桨封装的.NET版本OCR工具类库 - PaddleOCRSharp
前言 大家有使用过.NET开发过OCR工具吗?今天给大家推荐一个基于百度飞桨封装的.NET版本OCR工具类库:PaddleOCRSharp。 OCR工具有什么用? OCR(Optical Character Recognition)工具可以将图像或扫描文件中的文本内容转…...

在 CelebA 数据集上训练的 PyTorch 中的基本变分自动编码器
摩西西珀博士 一、说明 我最近发现自己需要一种方法将图像编码到潜在嵌入中,调整嵌入,然后生成新图像。有一些强大的方法可以创建嵌入或从嵌入生成。如果你想同时做到这两点,一种自然且相当简单的方法是使用变分自动编码器。 这样的深度网络不…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
