【电路笔记】-并联RLC电路分析
并联RLC电路分析
文章目录
- 并联RLC电路分析
- 1、概述
- 2、AC的行为
- 3、替代配置
- 3.1 带阻滤波器
- 3.2 带通滤波器
- 4、总结
电子器件三个基本元件的串联行为已在我们之前的文章系列 RLC 电路分析中详细介绍。 在本文中,介绍了另一种称为并联 RLC 电路的关联。
在第一部分中,我们介绍基本的并联 RLC 电路并重点关注其阻抗。
第二部分重点介绍并联 RLC 电路的交流行为。 我们重点介绍并解释了并联 L//C 配置引起的谐振现象,该配置解释了并联 RLC 电路的一些特性。
为了总结这两篇有关 RLC 电路的文章,最后一节介绍了替代配置。
1、概述
并联 RLC 电路由电阻器、电容器和电感器组成,它们在端子上共享相同的电压:

由于电压保持不变,因此并联配置的输入和输出被视为电流。
对于并联配置,总阻抗的倒数 ( Z R L C Z_{RLC} ZRLC) 是每个组件的倒数阻抗之和: 1 / Z R L C = 1 / Z R + 1 / Z L + 1 / Z C 1/Z_{RLC}=1/Z_R+1/Z_L+1/Z_C 1/ZRLC=1/ZR+1/ZL+1/ZC。 换句话说,电路的总导纳是每个元件的导纳之和。
该总导纳满足:

从等式1 可以清楚地看出,当 1 / L ω − C ω = 0 1/L\omega-C\omega=0 1/Lω−Cω=0 时,阻抗在特定的 ω \omega ω 值处达到峰值。 该脉动被称为共振脉动 ω 0 \omega_0 ω0(或共振频率 f 0 = ω 0 / 2 π f_0=\omega_0/2\pi f0=ω0/2π)并且由 ω 0 = 1 / L C \omega_0=1/\sqrt{LC} ω0=1/LC给出。
2、AC的行为
阻抗的快速分析可以揭示并联 RLC 电路的行为。 实际上考虑并联 RLC 电路的组件的以下值: R = 56 k Ω R=56k\Omega R=56kΩ、 L = 3 m H L=3 mH L=3mH 和 C = 5 μ F C=5\mu F C=5μF。
根据这些值,我们可以计算出系统的共振频率 ω 0 = 2.6 × 1 0 5 \omega_0=2.6×10^5 ω0=2.6×105 rad/s。 该电路由幅值为 5A 的交流电源供电,频率从DC 到 4 × 1 0 5 4×10^5 4×105rad/S。
图 2 是总阻抗和输出电流与提供给电路的角脉动 ω \omega ω的函数关系图:

该图清楚地表明,在谐振频率附近,电路的阻抗达到峰值,这导致在同一频率附近电流输出下降。
让我们关注电路中发生的情况,更准确地说是电容器和电感器之间发生的情况,以了解这种行为。 因此,首先考虑电容器初始充电的 L//C 配置。 下图显示了称为共振的循环中涉及的步骤:

图 3 中必须注释很多内容。首先,红色和绿色箭头分别表示电容器两端的电场和电感器两端的磁场。 箭头指示磁场的方向,充满电的组件用许多箭头表示,而放电的组件则没有箭头。
这些数字代表循环的步骤,数字8之后的下一步是步骤1。正如这一系列图中突出显示的,谐振现象是由于电容器和电感器之间发生的相互充电和放电造成的。 该循环发展的速度由共振频率 f 0 = 1 / ( 2 π L C ) f_0=1/(2\pi\sqrt{LC}) f0=1/(2πLC)给出。
在实际电路中,这个循环当然不是永久的,因为内部电阻通过焦耳加热来耗散能量。 然而,交流电源可以迫使电路维持电感器和电容器之间的电流交换。
具体来说,当 ω s o u r c e = ω 0 \omega_{source}=\omega_0 ωsource=ω0 时,能量交换最大,所有电流都在这两个组件之间流动,而主线中没有电流穿过电阻(见图 4)。 理解这一点的另一种方法是通过电抗的概念。 我们提醒您,电容器 ( X C X_C XC) 和电感器 (XL) 的电抗由下式给出:

由 ω 0 \omega_0 ω0的定义可知 X C ( ω 0 ) = X L ( ω 0 ) X_C(\omega_0)=X_L(\omega_0) XC(ω0)=XL(ω0)。 因此,由于电感器中 +90° 的相移和电容器中 –90° 的相移导致 180° 的相位差,组件上的电流相等,但方向相反。 这种现象可以在图 3 中的步骤 2 和 4 或步骤 6 和 8 中看到。
当工作在 ω 0 \omega_0 ω0 附近时,这种配置通常称为抑制电路。 我们将在下一节中详细介绍这一点,其中我们将展示 L//C 电路可以与电阻器串联以创建带阻滤波器。
3、替代配置
3.1 带阻滤波器
混合并联和串联设计的一种可能有趣的配置是与输出负载串联的并联 LC 滤波器,我们在下面将该电路称为 ( L / / C ) − R (L//C)-R (L//C)−R。 下面的图 4 给出了该架构的表示:

如果我们将 Z L / / C Z_{L//C} ZL//C 称为并联 LC 配置的阻抗,则可以写成 V i n = V o u t + Z L / / C × I V_{in}=V_{out}+Z_{L//C} \times I Vin=Vout+ZL//C×I。 知道 I = V o u t / R I=V_{out}/R I=Vout/R 并通过 V o u t V_{out} Vout 对表达式进行因式分解,我们可以在几步之后写出 (L//C)-R 电路的传递函数:

我们考虑 L = 3 m H L=3mH L=3mH、 C = 5 μ F C=5\mu F C=5μF、 R = 10 k Ω R=10k\Omega R=10kΩ 和 20 k Ω 20k\Omega 20kΩ。 绘制此传递函数后,我们会清楚地看到 (L//C)-R 电路充当带阻滤波器,其频率 ω 0 \omega_0 ω0 与基本并联 RLC 电路相同:

图5还强调了这样一个事实,即当电阻增加时,该带阻滤波器的带宽 △ ω \triangle\omega △ω变得更窄,这与RLC系列文章中给出的品质因数的定义相矛盾 Q s e r i e s = ( 1 / R ) L / C = ω 0 / △ ω Q_{series}=(1/R)\sqrt{L /C}=\omega_0/\triangle\omega Qseries=(1/R)L/C=ω0/△ω。
事实上,这个定义对于并联电路无效,并联配置的公式变为 Q p a r a l l e l = 1 / Q s e r i e s = R C / L Q_{parallel}=1/Q_{series}=R\sqrt{C/L} Qparallel=1/Qseries=RC/L,这解释了之前指出的图 4 中的行为。
并联RLC电路的特性参数实际上是串联RLC电路的倒数。
3.2 带通滤波器
一个有趣的概念,称为对偶性,使我们能够从另一个电路的知识中直接找到一个新电路的行为。 从以下事实推导出:适用于特定配置的电流或电压的方程可以应用于对偶配置的对偶量。
让我们更清楚一点,并再次考虑上面详细介绍的带阻滤波器示例。 我们将此配置称为 (L//C)-R,因为并联 (//) LC 电路与电阻 R 串联 (-)。我们已经看到该电路充当电压的带阻滤波器。
该电路的对偶是 (L//R)//R 电路,如图 6 所示:

对偶概念告诉我们,这个对偶电路充当带阻滤波器的对偶电路,带阻滤波器是带通滤波器。 为了验证这一结论,我们可以首先写下 I i n = I o u t + Y L / / C × V o u t I_{in}=I_{out}+Y_{L//C} \times V_{out} Iin=Iout+YL//C×Vout,这与上一节所示的方程相同,但适用于电流,如对偶概念所述。 Y L / / C Y_{L//C} YL//C 是配置 L//C 的导纳,等于 1 / Z L / / C 1/Z_{L//C} 1/ZL//C。
知道 V o u t = R × I o u t V_{out}=R \times I_{out} Vout=R×Iout并用 I o u t I_{out} Iout 对表达式进行因式分解,得到:

我们可以看到,方程 3 与方程 2 非常相似,但虚数项相反,这导致了带通滤波器的行为。 我们可以再次考虑相同的值 L = 3 m H L=3mH L=3mH、 C = 5 n F C=5 nF C=5nF、 R = 10 k Ω R=10k\Omega R=10kΩ 和 20 k Ω 20k\Omega 20kΩ,并绘制该传递函数,以便总结本节并确认带通滤波器:

4、总结
- 并联 RLC 电路的行为与串联配置有很大不同。 这是由于 L//C 电路的能量相互交换现象(称为谐振)造成的。
- 这种现象是由于互连的电感器和电容器之间发生相互放电/充电造成的。 理论上,这种电路的阻抗在称为谐振脉动(或 f0 的谐振频率)的特定脉动 ω0 处趋向于无限值。 在实际电路中,该阻抗由于内部电阻行为而达到峰值。
- 我们在上一节中已经看到,与输出负载串联集成可以制成带阻滤波器。 然而,并联连接会导致相反的滤波器:带通滤波器。
相关文章:

【电路笔记】-并联RLC电路分析
并联RLC电路分析 文章目录 并联RLC电路分析1、概述2、AC的行为3、替代配置3.1 带阻滤波器3.2 带通滤波器 4、总结 电子器件三个基本元件的串联行为已在我们之前的文章系列 RLC 电路分析中详细介绍。 在本文中,介绍了另一种称为并联 RLC 电路的关联。 在第一部分中&a…...

ros1 client
Client(客户端):发布海龟生成请求 [类似Publisher] Serve(服务端):海龟仿真器,接收请求 [类似于Subscriber] Service(服务):生成海龟的具体内容,其中服务类型…...
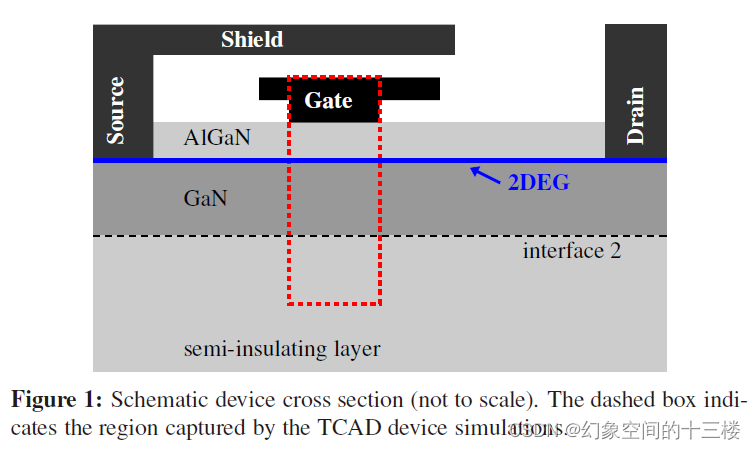
射频功率放大器应用中GaN HEMT的表面电势模型
标题:A surface-potential based model for GaN HEMTs in RF power amplifier applications 来源:IEEE IEDM 2010 本文中的任何第一人称都为论文的直译 摘要:我们提出了第一个基于表面电位的射频GaN HEMTs紧凑模型,并将我们的工…...
——EEG特征提取方法详解)
CSP(Common Spatial Patterns)——EEG特征提取方法详解
基于CSP的运动想象 EEG 特征提取和可视化参考前文:https://blog.csdn.net/qq_43811536/article/details/134273470?spm1001.2014.3001.5501 目录 1. CSP是什么?1.1 CSP的含义1.2 CSP算法1.3 CSP特征的特点 2. CSP特征在EEG信号分类任务中的应用2.1 任务…...
【Git】Git 学习笔记_操作本地仓库
1. 安装与初始化配置 1.1 安装 下载地址 在文件夹里右键点击 git bash here 即可打开命令行面板。 git -v // 查看版本1.2 配置 git config --global user.name "heo" git config --global user.email xxxgmail.com git config --global credential.helper stor…...
:在Pytorch中如何操作将数据集分为训练集和测试集?)
杂记(3):在Pytorch中如何操作将数据集分为训练集和测试集?
在Pytorch中如何操作将数据集分为训练集和测试集? 0. 前言1. 手动切分2. train_test_split方法3. Pytorch自带方法4. 总结 0. 前言 数据集需要分为训练集和测试集! 其中,训练集单纯用来训练,优化模型参数;测试集单纯用…...

【MySQL篇】数据库角色
前言 数据库角色是被命名的一组与数据库操作相关的权限,角色是权限的集合。因此,可以为一组具有相同权限的用户创建一个角色,使用角色来管理数据库权限可以简化授权的过程。 CREATE ROLE:创建一个角色 GRANT:给角色授…...
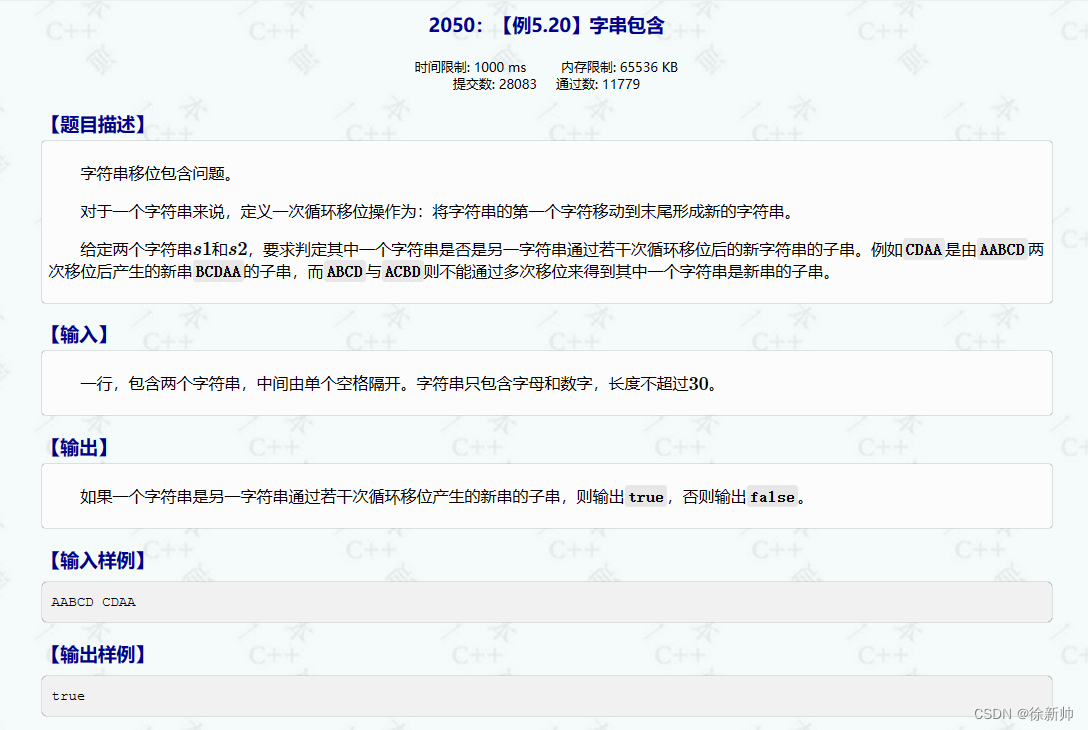
c++ 信奥赛编程 2050:【例5.20】字串包含
#include<iostream> #include<cstring> using namespace std; int main() {string str1,str2;int temp;cin>>str1>>str2;//判断长度 if(str1.size()<str2.size()){ swap(str1,str2); //交换内容 }str1str1str1; //AABCDAABCDAABCDAABCDif(str…...
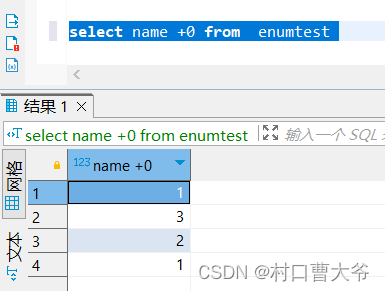
用dbeaver创建一个enum类型,并讲述一部分,mysql的enum类型的知识
写这个博客的目的就是我在网上看了半天,发现没有这方面的知识,也许是老手认为这个太简单了,不过我还是告诉新人使用dbeaver来创建一个enum类型的方法: 就是enum("a","b","name") 第一步用dbeaver…...
Paste v4.1.2(Mac剪切板)
Paste for Mac是一款运行在Mac OS平台上的剪切板小工具,拥有华丽的界面效果,剪切板每一条记录可显示(预览)文本,图片等记录的完整内容,可以记录最近指定条数的剪切板信息,方便用户随时调用&…...
事件绑定-回调函数
1.事件的概念 2.小程序常用的事件集 2.1 bindtap 点击回调事件方法 2.1.1语法格式 2.1.2 事件处理中调用data 使用setDatacount:这种方式 直接使用this.data.count 2.1.3 事件处理中传参 错误示范: 传递方式:数值用{{}},直接引…...

Makefile 总述
目录 一、Makefile 里有什么? 1、显式规则 2、隐晦规则 3、变量的定义 4、文件指示 5、注释 二、Makefile 的文件名 三、引用其它的 Makefile 四、环境变量 MAKEFILES 五、make 的工作方式 一、Makefile 里有什么? Makefile 里主要包含了五个东…...

写给新用户-Mac软件指南篇:让你的Mac更好用
用了macOS也有小四年了,今天打算分享一下Mac上的常用软件,说不上精通,但也算是有一些心得体会。平时也会定期对软件做整理,所以有了这篇文章。如果能帮到刚刚接触macOS或正在寻觅软件的你,那当然再好不过了。 软件推荐…...
03运算符综合
03 3.1.1算数运算符 3.1.2赋值运算符 3.1.3比较(关系)运算符 3.1.4逻辑运算符 3.1.5位运算符 3.2运算符的优先级 3.3条件表达式...

LeetCode刷题--思路总结记录
23-11-08每日一题:2609.最长平衡子字符串 链接:2609.最长平衡子字符串 总体思路: 平衡字符串要求“字符串前半段的0和后半段的1个数相同” > 分别记录0和1的计数结果,并最终取二者的最小值2字符串必须0开头,1结束 …...

Nodejs
node是运行js的环境 node 基础命令 // 初始化 // npm init // npm init -y// 全部选择yes // 安装包 // npm install 包名 // npm i// 安装package-lock.json里面所有的包到node_modules // npm i 包名// 安装当前最新版, // npm i 包名版本号//指定版本安装 // n…...

【面经】spring,springboot,springcloud有什么区别和联系
Spring、SpringBoot、SpringCloud都是Java开发中的重要框架,它们的作用和区别如下: Spring:是一个轻量级的开源框架,是为解决企业应用开发的复杂性而创建的。它提供了AOP(面向切面编程)和Ioc(控…...

SpringBoot Kafka消费者 多kafka配置
一、配置文件 xxxxxx:kafka:bootstrap-servers: xx.xx.xx.xx:9092,xx.xx.xx.xx:9092consumer:poll-timeout: 3000key-deserializer: org.apache.kafka.common.serialization.StringDeserializervalue-deserializer: org.apache.kafka.common.serialization.StringDeserializer…...

git 标签相关命令
要在本地仓库中添加标签,你可以使用以下命令: git tag <tag_name> 这将在当前所处的提交上创建一个轻量级标签(lightweight tag)。如果你想要创建一个带有附注信息的标签,可以使用 -a 选项: git t…...

我在Vscode学OpenCV 图像运算(权重、逻辑运算、掩码、位分解、数字水印)
文章目录 权重 _ 要求两幅图像是相同大小的。[ 1 ] 以数据说话( 1) 最终:( 2 )gamma _输出图像的标量值 [ 2 ] 图像的展现力gamma并不等同于增加曝光度( 1 )gamma100( 2 )…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
