【数据结构】树与二叉树(五):二叉树的顺序存储(初始化,插入结点,获取父节点、左右子节点等)
文章目录
- 5.1 树的基本概念
- 5.1.1 树的定义
- 5.1.2 森林的定义
- 5.1.3 树的术语
- 5.1.4 树的表示
- 5.2 二叉树
- 5.2.1 二叉树
- 5.2.2 二叉树顺序存储
- 典例
- 例题
- C语言实现
- 答案
5.1 树的基本概念
5.1.1 树的定义
- 一棵树是结点的有限集合T:
- 若T非空,则:
- 有一个特别标出的结点,称作该树的根,记为root(T);
- 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0),其中T1, T2, …, Tm又都是树,称作root(T)的子树。
- T 空时为空树,记作root(T)=NULL。
- 若T非空,则:
5.1.2 森林的定义
一个森林是0棵或多棵不相交(非空)树的集合,通常是一个有序的集合。换句话说,森林由多个树组成,这些树之间没有交集,且可以按照一定的次序排列。在森林中,每棵树都是独立的,具有根节点和子树,树与树之间没有直接的连接关系。
森林是树的扩展概念,它是由多个树组成的集合。在计算机科学中,森林也被广泛应用于数据结构和算法设计中,特别是在图论和网络分析等领域。
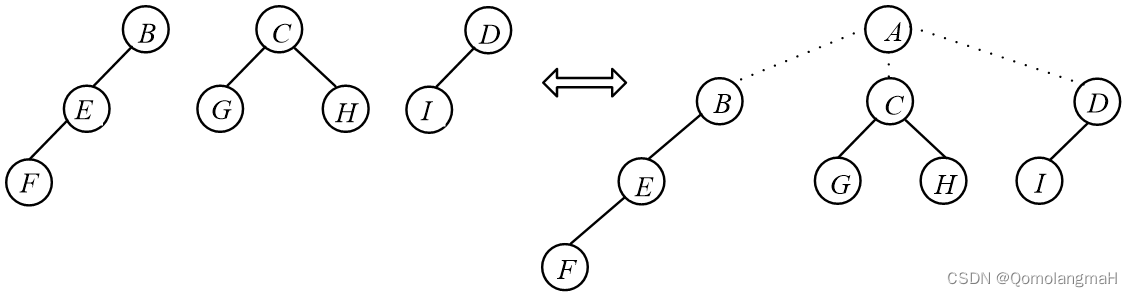
5.1.3 树的术语
- 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(ancestor)
- 度(degree)、叶子节点(leaf node)、分支节点(internal node)
- 结点的层数
- 路径、路径长度、结点的深度、树的深度
参照前文:【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
5.1.4 树的表示
- 【数据结构】树与二叉树(二):树的表示C语言:树形表示法、嵌套集合表示法、嵌套括号表示法 、凹入表示法
5.2 二叉树
5.2.1 二叉树
1. 定义
二叉树是一种常见的树状数据结构,它由结点的有限集合组成。一个二叉树要么是空集,被称为空二叉树,要么由一个根结点和两棵不相交的子树组成,分别称为左子树和右子树。每个结点最多有两个子结点,分别称为左子结点和右子结点。
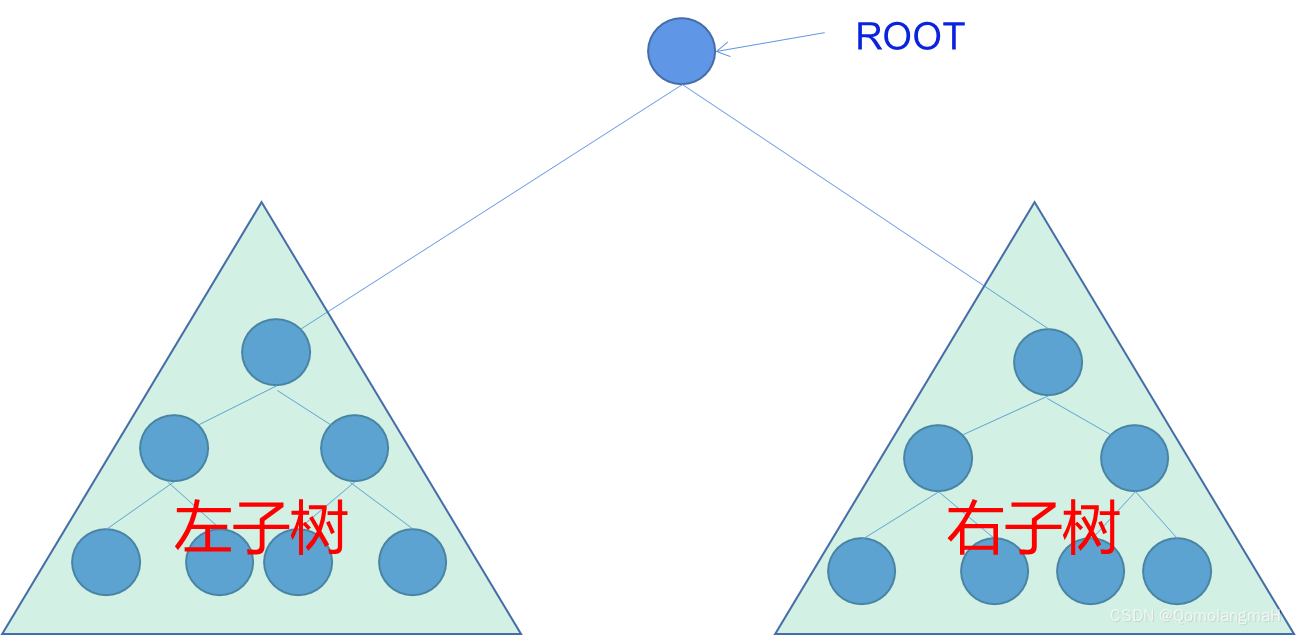
2. 特点
二叉树的特点是每个结点最多有两个子结点,并且子结点的位置是有序的,即左子结点在前,右子结点在后。这种有序性使得二叉树在搜索、排序等算法中有广泛的应用。
-
在二叉树中,根结点是整个树的起始点,通过根结点可以访问到整个树的其他结点。每个结点都可以看作是一个独立的二叉树,它的左子树和右子树也是二叉树。
-
二叉树可以是空树,也可以是只有根结点的树,或者是由多个结点组成的树。每个结点可以包含一个数据元素,以及指向左子结点和右子结点的指针。
-
二叉树的形状可以各不相同,它可以是平衡的或者不平衡的,具体取决于结点的分布情况。在二叉树中,每个结点的左子树和右子树都是二叉树,因此可以通过递归的方式来处理二叉树的操作。
3. 性质
引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。
引理5.2:高度为k的二叉树中至多有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。
引理5.3:设T是由n个结点构成的二叉树,其中叶结点个数为 n 0 n_0 n0,度数为2的结点个数为 n 2 n_2 n2,则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
- 详细证明过程见前文:【数据结构】树与二叉树(三):二叉树的定义、特点、性质及相关证明
4. 满二叉树
定义5.3:一棵非空高度为 k ( k ≥ 0 ) k( k≥0) k(k≥0)的满二叉树(perfect binary tree),是有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点的二叉树。
5. 完全二叉树
定义5.4:一棵包含 n n n个节点、高度为 k k k的二叉树 T T T,当按层次顺序编号 T T T的所有节点,对应于一棵高度为 k k k的满二叉树中编号由1至 n n n的那些节点时, T T T被称为完全二叉树(complete binary tree)。
- 满二叉树、完全二叉树性质及证明:【数据结构】树与二叉树(四):满二叉树、完全二叉树及其性质
5.2.2 二叉树顺序存储
二叉树的顺序存储是指将二叉树中所有结点按层次顺序存放在一块地址连续的存储空间中
对于完全二叉树,结点的层次顺序反映了其结构,可按层次顺序给出一棵完全二叉树之结点的编号,事实上,这就是完全二叉树的顺序存储方法,结点编号恰好反映了结点间的逻辑关系。
只要对完全二叉树之结点按照层次顺序进行编号,就可利用一维数组 A A A来存储一棵含有 n n n个结点的完全二叉树,其中A[1]存储二叉树的根结点,A[i]存储二叉树中编号为i的结点,并且结点A[i]的左儿子(若存在)存放在A[2i]处,而A[i]的右儿子(若存在)存放在A[2i+1]处。注意,这里我们约定数组索引从1开始,而不是从0开始,在使用数组存储完全二叉树时,需要留出A[0]位置不使用。
典例
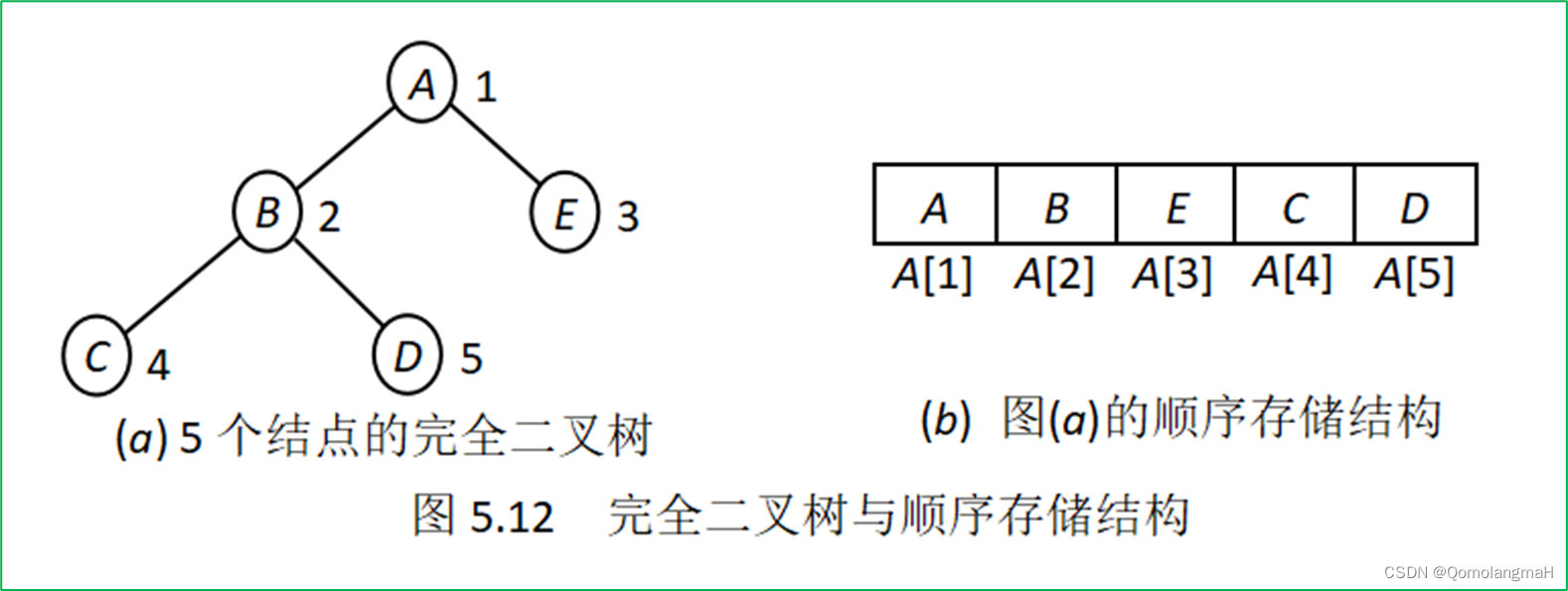
首先,我们按照完全二叉树的结点顺序进行编号,从上到下、从左到右依次编号。根据给出的完全二叉树,我们可以得到以下结点编号:
1/ \2 3/ \4 5
接下来,我们可以利用一维数组来存储这棵完全二叉树。创建一个大小为6的数组A,其中A[1]表示根结点 A A A,A[2]表示结点 B B B,A[3]表示结点 E E E,A[4]表示结点 C C C,A[5]表示结点 D D D。
索引: 1 2 3 4 5
数组: [ A, B, E, C, D ]
根据完全二叉树的性质,结点 A A A的左儿子应该存放在A[2]的位置,右儿子应该存放在A[3]的位置。结点 B B B的左儿子应该存放在A[4]的位置,右儿子应该存放在A[5]的位置。
例题
画出下面这棵完全二叉树的顺序存储结构:
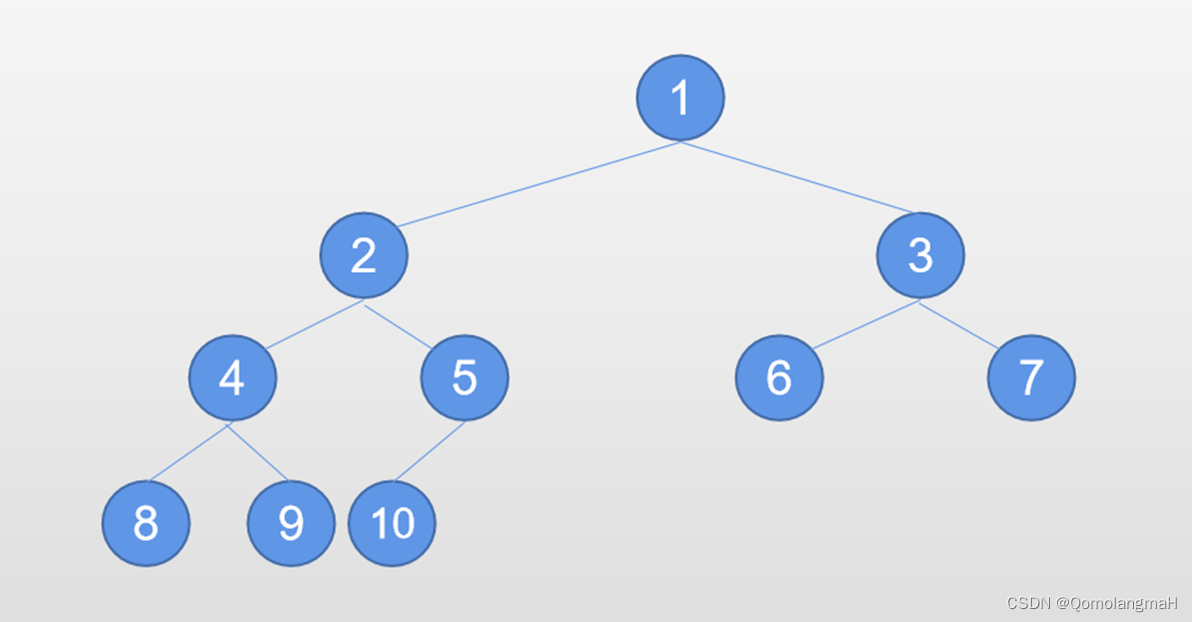
答案见文末 答案见文末 答案见文末
完全二叉树的顺序存储方式是一种简单且节省空间的存储方式。它只需要使用一个一维数组来存储完全二叉树的结点信息域的值,而不需要额外的空间来存储左儿子和右儿子的地址。
通过计算结点的编号和数组索引之间的关系,我们可以方便地找到结点的左儿子、右儿子和父亲结点。例如,对于结点i,它的左儿子的编号是2i,右儿子的编号是2i+1,父亲结点的编号是⌊i/2⌋。这种计算关系使得寻找子孙结点和祖先结点变得非常方便和高效。
顺序存储方式的优点是节省了存储空间,同时访问结点也非常快速,因为可以通过数组索引直接访问结点,而不需要进行指针的跳转。然而,顺序存储方式也有一些限制。由于使用数组存储,需要提前确定完全二叉树的最大结点个数,因此对于结点数不确定或者动态变化的情况下,顺序存储方式可能不适用。
C语言实现
注意,这里我们约定数组索引从0开始,节点位置计算公式与前文略有不同。
#include <stdio.h>
#include <stdlib.h>#define MAX_SIZE 100 // 定义数组的最大大小// 二叉树的顺序存储结构
typedef struct {char data[MAX_SIZE]; // 数组用于存储结点的数据int size; // 二叉树的大小(结点个数)
} BinaryTree;// 初始化二叉树
void initBinaryTree(BinaryTree* tree) {tree->size = 0;
}// 向二叉树中插入结点
void insertNode(BinaryTree* tree, int value, int index) {if (tree->size >= MAX_SIZE) {printf("Binary tree is full. Cannot insert more nodes.\n");return;}if (index < 0 || index > tree->size) {printf("Invalid index.\n");return;}// 将插入位置后的结点后移for (int i = tree->size - 1; i >= index; i--) {tree->data[i + 1] = tree->data[i];}// 插入新结点tree->data[index] = value;tree->size++;
}// 获取结点的父节点编号
int getParentIndex(int index) {return (index - 1) / 2;
}// 获取结点的左子节点编号
int getLeftChildIndex(int index) {return 2 * index + 1;
}// 获取结点的右子节点编号
int getRightChildIndex(int index) {return 2 * index + 2;
}// 根据索引获取结点的值
char getNodeValue(BinaryTree* tree, int index) {if (index >= tree->size || index < 0) {printf("Invalid index.\n");return -1;}return tree->data[index];
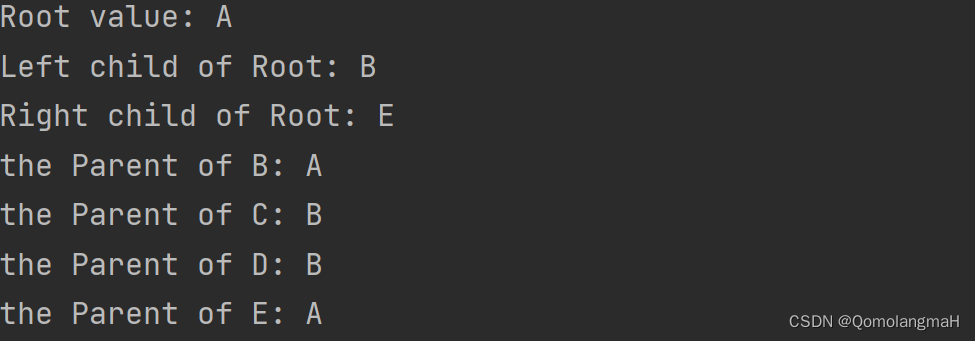
}int main() {BinaryTree tree;initBinaryTree(&tree);// 向二叉树中插入结点insertNode(&tree, 'A', 0); insertNode(&tree, 'B', 1); insertNode(&tree, 'E', 2); insertNode(&tree, 'C', 3); insertNode(&tree, 'D', 4); // 获取结点的值和子节点的值char rootValue = getNodeValue(&tree, 0);char leftChildValue = getNodeValue(&tree, getLeftChildIndex(0));char rightChildValue = getNodeValue(&tree, getRightChildIndex(0));printf("Root value: %c\n", rootValue);printf("Left child of Root: %c\n", leftChildValue);printf("Right child of Root: %c\n", rightChildValue);printf("the Parent of B: %c\n", getNodeValue(&tree, getParentIndex(1)));printf("the Parent of C: %c\n", getNodeValue(&tree, getParentIndex(3)));printf("the Parent of D: %c\n", getNodeValue(&tree, getParentIndex(4)));printf("the Parent of E: %c\n", getNodeValue(&tree, getParentIndex(2)));return 0;
}
答案


相关文章:

【数据结构】树与二叉树(五):二叉树的顺序存储(初始化,插入结点,获取父节点、左右子节点等)
文章目录 5.1 树的基本概念5.1.1 树的定义5.1.2 森林的定义5.1.3 树的术语5.1.4 树的表示 5.2 二叉树5.2.1 二叉树1. 定义2. 特点3. 性质引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。引理5.2:高度为k的二叉…...
【HarmonyOS】HarmonyOS备案获取公钥和指纹
【关键字】 HarmonyOS应用、鸿蒙应用、元服务、应用备案 HarmonyOS应用在华为云等平台进行应用备案时,平台需要提供用公钥和签名指纹的信息,Android可以直接通过keystore或jks签名文件进行签名信息获取,HarmonyOS签名方式与Android不同&…...
,多数据源+Mybatisplus + Sharding JDBC同一库中分表
水平分表是在同一个数据库内,把同一个表的数据按一定规则拆到多个表中,多数据源采用 mybatis-plus的dynamic-datasource 分库分表采用sharding-jdbc 数据库连接池管理是alibaba的druid-spring-boot-starter 同一个数据库内分表 目录 1.数据库表 2.配置 3.引入的…...
Docsify 和 Hugo 之间的选型
对文档的编译,目前的发布方案是越来越注重 MD 的编辑和发布。 针对其他 Wiki 的选择,MD 文件的编辑通常会保留修改记录,同时不依赖中央数据库和其他类型的 Web 应用服务。 随着各大云平台的支持,包括 GitHub Page 和 Google 的 …...

第二十章 ObjectScript 应用程序中的数值计算 - 转换:十进制到 $DOUBLE
文章目录 第二十章 ObjectScript 应用程序中的数值计算 - 转换:十进制到 $DOUBLE 转换:十进制到 $DOUBLE转换:$DOUBLE 到十进制$DECIMAL(x)$DECIMAL(x, n) 转换:十进制到字符串 第二十章 ObjectScript 应用程序中的数值计算 - 转…...
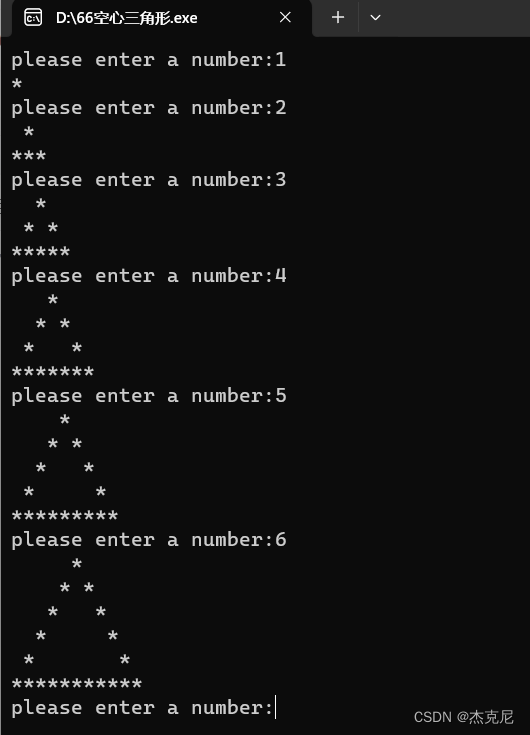
C语言【趣编程】我们怎样便捷输出空心的金字塔
目录 1问题: 2解题思路: 3代码如下: 4代码运行结果如下图所示: 5总结: r如若后续有不会的问题,可以和我私聊; 1问题: 2解题思路: 方法:找规律࿰…...

《JavaScript设计模式》笔记 - - - 超全设计模式概览
该篇文章用于记录阅读《JavaScript设计模式》后归纳的读书笔记,主要以代码形式进行展示,用于快速回顾对应设计模式的代码构造 1.面向对象编程 1.使用对象收编变量 优点:避免全局变量冲突与覆盖 缺点:不利于复用 var CheckObj {c…...

浅谈Vue 3的响应式对象: ref和reactive
Vue 3是一个流行的前端框架,它引入了一些新的特性来提高开发者的体验和性能。其中,响应式对象是 Vue 3 中一个非常重要的概念。在这篇博客中,我们将重点介绍 Vue 3 中的响应式对象,并深入探讨其中的 ref 和 reactive。 引言 在现…...
怎么学编程效率高,编程练习网站编程软件下载,中文编程开发语言工具下载
怎么学编程效率高,编程练习网站编程软件下载,中文编程开发语言工具下载 给大家分享一款中文编程工具,零基础轻松学编程,不需英语基础,编程工具可下载。 这款工具不但可以连接部分硬件,而且可以开发大型的…...

Alphago Zero的原理及实现:Mastering the game of Go without human knowledge
近年来强化学习算法广泛应用于游戏对抗上,通用的强化学习模型一般包含了Actor模型和Critic模型,其中Actor模型根据状态生成下一步动作,而Critic模型估计状态的价值,这两个模型通过相互迭代训练(该过程称为Generalized …...
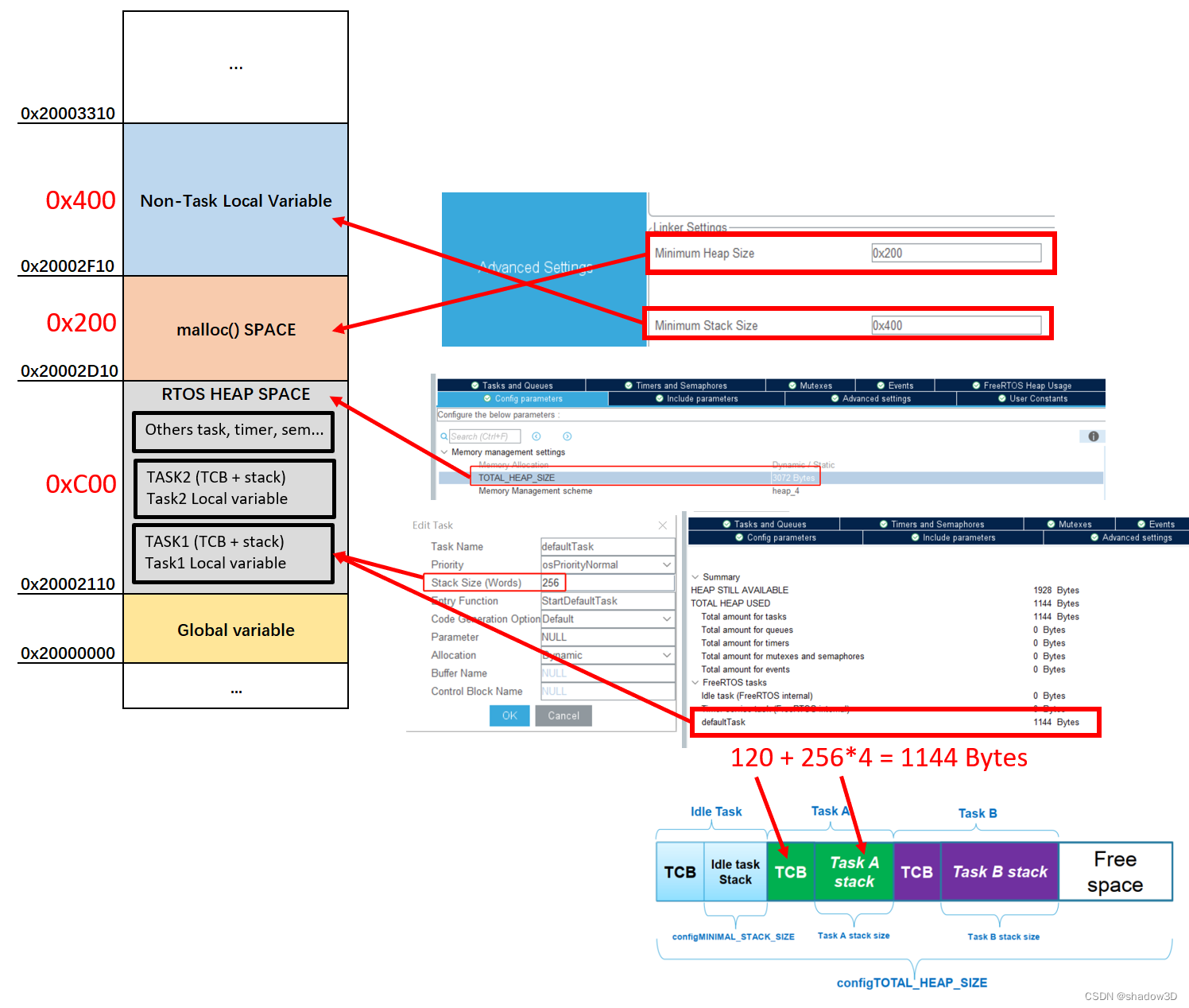
STM32 堆栈空间分布
参考 运行时访问__initial_sp和__heap_base 无RTOS时的情况 在以上配置的情况下,生成工程。在工程的startup.s文件中,由如下代码: Stack_Size EQU 0x400AREA STACK, NOINIT, READWRITE, ALIGN3 __Stack_top ; 自己添加 Stack_Mem…...

小程序制作(超详解!!!)第十五节 自动随机变化的三色旗
1.例题描述 设计一个小程序,开始时界面上显示一个三色旗和一个按钮,当点击按钮时,三色旗的颜色会发生随机变化,即使不点击按钮,三色旗的颜色也会每隔一定时间自动发生变化。 2.index.wxml <view class"box&…...

MySQL_主从复制_环境搭建
MySQL主从复制配置 CentOS 7 配置 阿里云 yum 源 sudo mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.backup sudo wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repo sudo yum clean all sudo yum makeca…...
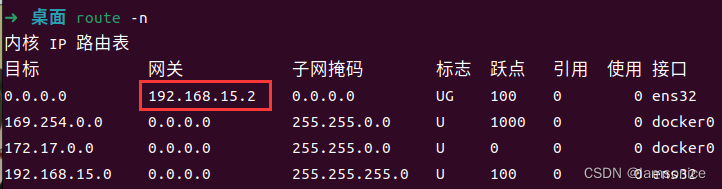
Linux 设置静态IP(Ubuntu 20.04/18.04)
以Ubuntu20.04示例 第一步:查看当前网络信息 ifconfig 本机网卡名为:ens32,IP地址为:192.168.15.133,子网掩码为:255.255.255.0 第二步:查看当前网关信息 route -n 网关地址为:1…...
计网----累积应答,TCP的流量控制--滑动窗口,粘包问题,心跳机制,Nagle算法,拥塞控制,TCP协议总结,UDP和TCP对比,中介者模式
计网----累积应答,TCP的流量控制–滑动窗口,粘包问题,心跳机制,Nagle算法,拥塞控制,TCP协议总结,UDP和TCP对比,中介者模式 一.累积应答 1.什么是累计应答 每次发一些包࿰…...

OpenCV 直方图和归一化
直方图可以反映图片的整体统计信息, 使用函数 CalcHist() 实现. 但CalcHist() 统计出的数量信息和图像大小相关, 如果要剔除图像大小因素, 需要做归一化处理, 归一化处理后的信息, 反映出各个颜色值得占比情况, 这样更方便不同size图像做对比, 归一化的函数为 Normalize(). ///…...
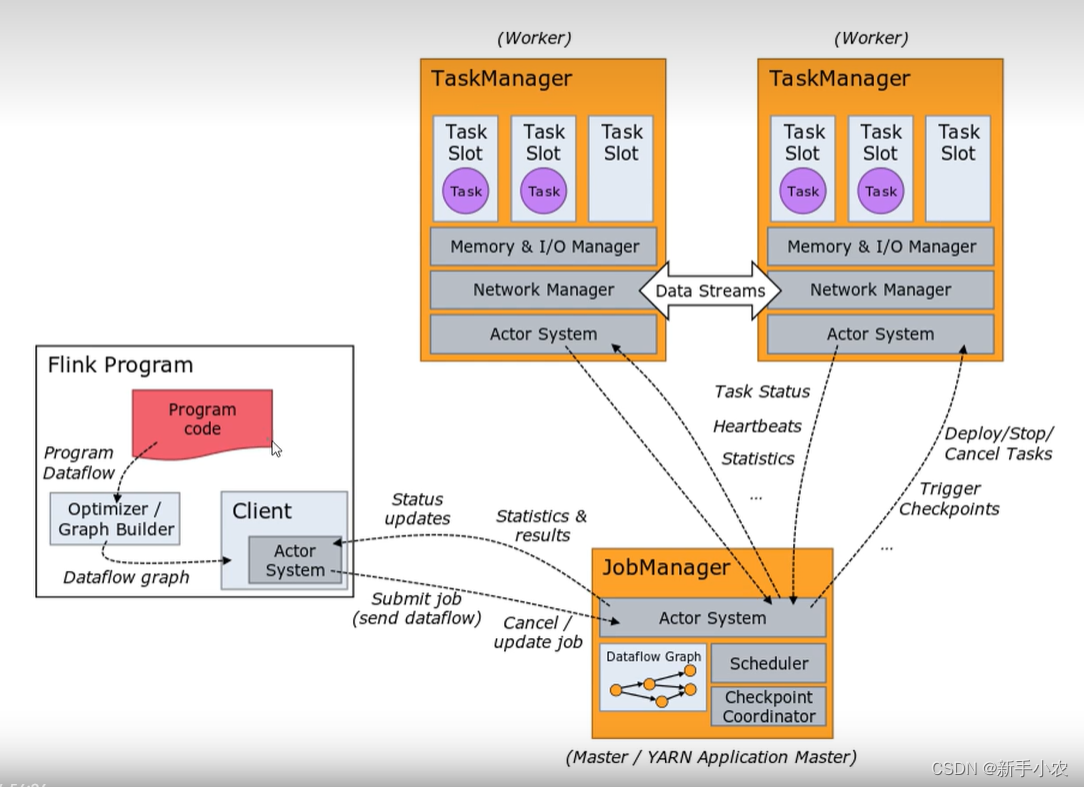
Flink架构
1、Apache Flink集群的核心架构: 1、client(作业客户端):提交任务的地方叫做客户端 2、JobManager(作业管理器):作用是用于管理集群中任务 3、TaskManager(任务管理器)&a…...

Packet Tracer路由器连接终端设备怎么配置?
在Packet Tracer中配置一台路由器和三台终端设备可以帮助你建立一个简单的局域网,以下是配置的基本步骤: 打开Packet Tracer,从左侧设备栏中拖拽一个路由器和三个终端设备到工作区。 连接设备:使用网线将路由器的端口与每台终端设…...

评估APP网页小程序代码UI开发H5估价师怎么评估开发精确研发价格?
作为一名应用程序开发评估师,可能涉及到的主要任务是为特定的应用程序提供估算开发成本和所需时间预测。为了为一个应用程序更准确地评估价格,须遵循以下几个步骤: 问: 如何让一个App更好、更精确地评估出价格? 答: 以下是一个可…...

16 Linux 内核定时器
一、Linux 时间管理和内核定时器简介 1. 内核时间管理简介 Linux 内核中有大量的函数需要时间管理,比如周期性的调度程序、延时程序、定时器等。 硬件定时器提供时钟源,时钟源的频率可以设置,设置好以后就周期性的产生定时中断,系…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
