【排序算法】 快速排序(快排)!图解+实现详解!

文章目录
- 📑前言
- 🌤️快速排序的概念
- ☁️快速排序的由来
- ☁️快速排序的思想
- ☁️快速排序的实现步骤
- 🌤️快速排序(递归版)
- ☁️快排主框架
- ☁️Hoare版本快排
- ⭐代码与图解
- ⭐代码解析:
- ☁️挖坑法
- ⭐代码与图解
- ⭐代码解析:
- ☁️双指针法
- ⭐代码与图解
- ⭐代码解析
- ☁️三数取中优化
- ⭐为什么要三数取中?
- ⭐三数取中代码实现
- ☁️小区间优化
- ⭐什么是区间优化?
- ⭐小区间优化代码实现
- ⭐小区间优化的好处
- 🌤️快速排序(非递归版)
- ☁️代码解析
- 🌤️快速排序的特性总结
- 🌤️全篇总结
📑前言
什么是快排?快排的速度到底有多快呢?它们的思想和实现是什么样的?
本文会对这快速排序进行详解,绝对细致入微!让你彻底搞懂快排!
🌤️快速排序的概念
☁️快速排序的由来
英国计算机科学家Tony Hoare在1960年为了解决计算机上的排序问题,提出了快速排序的算法,最初是为了在英国的英尔兰电子公司(ELLIOTT Brothers)的快速硬件上实现高效的排序算法。
☁️快速排序的思想
快速排序的主要思想是分治法,将一个大问题分割成小问题,解决小问题后再合并它们的结果。
☁️快速排序的实现步骤
- 从待排序的数组中选择一个元素,称之为枢纽元(pivot)。
- 将数组中小于枢纽元的元素移到枢纽元的左边,将大于枢纽元的元素移到枢纽元的右边,这个过程称为分区(partition)。
- 递归地对枢纽元左边的子数组和右边的子数组进行排序。
- 当所有子数组都有序时,整个数组就自然有序了。
🌤️快速排序(递归版)
☁️快排主框架
void QuickSort(int* a, int left, int right)
{
// 假设按照升序对array数组中[left, right)区间中的元素进行排序if (right <= left)return;
// 按照基准值对array数组的 [left, right)区间中的元素进行划分//int keyi = PartSort1(a, left, right);//int keyi = PartSort2(a, left, right);int keyi = PartSort3(a, left, right);
// 划分成功后以div为边界形成了左右两部分 [left, keyi-1) 和 [keyi+1, right)
// 递归排[left, keyi-1)QuickSort(a, left, keyi - 1);
// 递归排[keyi+1, right)QuickSort(a, keyi + 1, right);
}
上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,在写递归框架时想想二叉树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。
☁️Hoare版本快排
⭐代码与图解

int PartSort1(int* a, int left, int right)
{//三数取中(优化)//int keyi = NumBers(a, left, right);//Swap(&a[keyi], &a[left]);int key = left;while (left < right){while (left < right && a[left] <= a[right]){right--;}while (left < right && a[left] <= a[right]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[key]);return left;
}
⭐代码解析:
- 首先,定义一个变量key,用于保存基准值的下标,初始值为left。
- 进入一个循环,循环条件是left < right,即左右指针没有相遇。
- 在循环中,首先从右边开始,找到第一个小于等于基准值的元素的下标,将right指针左移,直到找到符合条件的元素或者left和right相遇。
- 然后从左边开始,找到第一个大于基准值的元素的下标,将left指针右移,直到找到符合条件的元素或者left和right相遇。
- 如果left < right,说明找到了需要交换的元素,将a[left]和a[right]交换位置。
- 重复步骤3到步骤5,直到left和right相遇。
- 最后,将基准值a[key]和a[left]交换位置,将基准值放在正确的位置上。
- 返回分割点的下标left。
实现了一次快速排序的分割操作,将数组分成两部分,左边的元素都小于等于基准值,右边的元素都大于基准值。然后再通过递归调用这个函数,这就是hoare版的快排。
☁️挖坑法
⭐代码与图解

int PartSort2(int* a, int left, int right)
{//三数取中优化//int keyi = NumBers(a, left, right);//Swap(&a[keyi], &a[left]);int key = a[left];int hole = left;//为第一个坑while (left < right){while (left < right && key <= a[right]){--right;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;return hole;
}
⭐代码解析:
- 定义一个变量key,用于保存基准值,初始值为a[left]。
- 定义一个变量hole,用于保存空洞的位置,初始值为left。
- 进入一个循环,循环条件是left < right,即左右指针没有相遇。
- 在循环中,首先从右边开始,找到第一个小于基准值的元素的下标,将right指针左移,直到找到符合条件的元素或者left和right相遇。
- 将a[right]的值赋给a[hole],将空洞的位置移动到right。
- 然后从左边开始,找到第一个大于基准值的元素的下标,将left指针右移,直到找到符合条件的元素或者left和right相遇。
- 将a[left]的值赋给a[hole],将空洞的位置移动到left。
- 重复步骤4到步骤7,直到left和right相遇。
- 最后,将基准值key放入空洞的位置a[hole],将基准值放在正确的位置上。
- 返回空洞的位置hole。
同样实现了将数据分成两部分,左边的元素都小于等于基准值,右边的元素都大于基准值。
☁️双指针法
⭐代码与图解

// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{//三数取中优化//int midi = NumBers(a, left, right);//Swap(&a[left], &a[midi]);int prev = left;int cur = prev + 1;int keyi = left;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[keyi]);return prev;
}
⭐代码解析
- 定义两个指针prev和cur,分别指向left和left+1。
- 定义一个变量keyi,用于保存基准值的下标,初始值为left。
- 进入一个循环,循环条件是cur <= right,即cur指针没有越界。
- 在循环中,如果a[cur]小于基准值a[keyi],则将prev指针右移一位,并交换a[prev]和a[cur]的值,保证prev指针之前的元素都小于基准值。
- 将cur指针右移一位。
- 重复步骤4到步骤6,直到cur指针越界。
- 最后,将基准值a[keyi]和a[prev]交换位置,将基准值放在正确的位置上。
- 返回分割点的下标prev。
同样实现了将数据分成两部分,左边的元素都小于等于基准值,右边的元素都大于基准值。
☁️三数取中优化
⭐为什么要三数取中?
-
三数取中是为了选择一个更好的基准值,以提高快速排序的效率。在快速排序中,选择一个合适的基准值是非常重要的,它决定了每次分割的平衡性。
-
快速排序是通过一趟排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的小,然后再对这两部分分别进行快速排序,递归地进行下去,直到整个序列有序。
-
如果每次选择的基准值都是最左边或最右边的元素,那么在某些情况下,快速排序的效率可能会降低。例如,当待排序序列已经有序时,如果每次选择的基准值都是最左边或最右边的元素,那么每次分割得到的两个子序列的长度差可能会非常大,导致递归深度增加,快速排序的效率降低。
-
而通过三数取中的优化,可以选择一个更好的基准值,使得每次分割得到的两个子序列的长度差更小,从而提高快速排序的效率。
-
具体来说,三数取中的优化是选择待排序序列的左端、右端和中间位置的三个元素,然后取它们的中值作为基准值。这样选择的基准值相对于最左边或最右边的元素,更接近整个序列的中间位置,可以更好地平衡分割后的两个子序列的长度,从而提高快速排序的效率。
-
通过三数取中的优化,可以减少递归深度,提高分割的平衡性,使得快速排序的效率更稳定,适用于各种不同的输入情况。
⭐三数取中代码实现
//三数取中
int NumBers(int* a, int left, int right)
{int mid = (left + right) / 2;// left mid rightif (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]) // mid是最大值{return left;}else{return right;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]) // mid是最小{return left;}else{return right;}}
}
☁️小区间优化
⭐什么是区间优化?
小区间优化是指在快速排序中,当待排序的子序列的长度小于一定阈值时,不再继续使用快速排序,而是转而使用直接插入排序。
⭐小区间优化代码实现
void QuickSort(int* a, int left, int right)
{if (right <= left)return;if(right - left + 1 > 10){int keyi = PartSort3(a, left, right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}else{InsertSort(a + left,right - left + 1);}
}
⭐小区间优化的好处
- 减少递归深度:使用插入排序来处理较小的子序列,可以减少递归的深度,从而减少了函数调用的开销。
- 提高局部性:插入排序是一种稳定的排序算法,它具有良好的局部性,可以充分利用已经有序的部分序列。对于较小的子序列,插入排序的效率更高。
- 减少分割次数:对于较小的子序列,使用插入排序可以减少分割的次数。快速排序的分割操作需要移动元素,而插入排序只需要进行元素的比较和交换,因此在较小的子序列中使用插入排序可以减少分割操作的次数。
小区间优化可以在一定程度上提高快速排序的性能。它通过减少递归深度、提高局部性和减少分割次数来优化算法的效率,特别适用于处理较小的子序列。
🌤️快速排序(非递归版)
这里需要借助栈的来实现非递归.关于栈详情见:数据结构剖析–栈
// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{Stack st;StackInit(&st);StackPush(&st, right);StackPush(&st, left);while (!StackEmpty(&st)){int begin = StackTop(&st);StackPop(&st);int end = StackTop(&st);StackPop(&st);int keyi = PartSort3(a, begin, end);if (keyi + 1 < end){StackPush(&st, end);StackPush(&st, keyi + 1);}if (begin < keyi - 1){StackPush(&st, keyi - 1);StackPush(&st, begin);}}StackDestroy(&st);
}
☁️代码解析
- 将整个序列的起始和结束位置入栈。然后,进入循环,不断从栈中取出子序列的起始和结束位置。
- 在每次循环中,通过PartSort3函数将当前子序列分割成两部分,并得到基准值的下标keyi。如果基准值右边的子序列长度大于1,则将右边子序列的起始和结束位置入栈。如果基准值左边的子序列长度大于1,则将左边子序列的起始和结束位置入栈。
- 循环继续,直到栈为空,表示所有的子序列都已经排序完成。
通过使用栈来模拟递归的过程,非递归实现避免了递归调用的开销,提高了快速排序的效率。
🌤️快速排序的特性总结
-
快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
-
时间复杂度:O(N*logN)

-
空间复杂度:O(logN)
-
稳定性:不稳定
🌤️全篇总结
本章对快排从其思想到实现,一步步由浅入深的讲解,相信聪明的你看到这里已经对快排有一个明白的理解了!
看到这里希望给博主留个:👍点赞🌟收藏⭐️关注!

相关文章:

【排序算法】 快速排序(快排)!图解+实现详解!
🎥 屿小夏 : 个人主页 🔥个人专栏 : 算法—排序篇 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言🌤️快速排序的概念☁️快速排序的由来☁️快速排序的思想☁️快速排序的实…...

急招开发、安全工程师实习生
信息安全工程师-实习生 公司:四川久远银海软件股份有限公司 工作职责 1、负责对公司WEB应用、APP、小程序、公众号等产品进行安全渗透测试; 2、负责对参与攻防演练、护网行动的项目组提供安全技术支撑; 3、负责提供基线核查、风险评估、主…...
数据结构与算法—插入排序选择排序
目录 一、排序的概念 二、插入排序 1、直接插入排序 直接插入排序的特性总结: 2、希尔排序 希尔排序的特性总结: 三、选择排序 1、直接选择排序 时间复杂度 2、堆排序—排升序(建大堆) 向下调整函数 堆排序函数 代码完整版: …...

基于词云图的短信热词数据可视化
热词统计:短信、邮件、微信、QQ、微博、电商评价、新闻、各行业热词(旅游、世界杯、战争、考研等)、热点事件等场景。 展示模型:给定多段文本,绘制出词云图。 核心思想:根据样本集中的文本包含的高频词…...
Linux/centos上如何配置管理Web服务器?
Linux/centos上如何配置管理Web服务器? 1 Web简单了解2 关于Apache3 如何安装Apache服务器?3.1 Apache服务安装3.2 httpd服务的基本操作 4 如何配置Apache服务器?4.1 关于httpd.conf配置4.2 常用指令 5 简单实例 1 Web简单了解 Web服务器称为…...
Java EE进阶2
包如果下载不下来怎么办? 1,确认包是否存在 2.如果包存在就多下载几次 3.如果下载了很多次都下载不下来,看看是不是下面几步出现了问题? 1)是否配置了国内源 settings.xml 2)目录是否为全英文,存在中文的话就修改路径 3)删除本地仓库的 jar 包,重新下载(可能由于网络的原…...

最新AI系统ChatGPT源码+AI绘画系统源码+支持GPT4.0+Midjourney绘画+搭建部署教程+附源码
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如…...

大厂面试题-为什么一线互联网公司严禁使用存储过程
之所以互联网公司不让用,主要有几个方面的原因: 1.存储过程不好调试,一旦涉及到非常复杂的逻辑,定位问题的时候比较麻烦 2.存储过程的一致性很差,如果从Oracle迁移到MySQL,涉及到部分数据库独有特性的时候…...

SpringBoot+Swagger详细使用方法
一、接口文档概述 swagger是当下比较流行的实时接口文文档生成工具。接口文档是当前前后端分离项目中必不可少的工具,在前后端开发之前,后端要先出接口文档,前端根据接口文档来进行项目的开发,双方开发结束后在进行联调测试。 二…...
[动态规划] (十二) 简单多状态 LeetCode 213.打家劫舍II
[动态规划] (十二) 简单多状态: LeetCode 213.打家劫舍II 文章目录 [动态规划] (十二) 简单多状态: LeetCode 213.打家劫舍II题目解析解题思路状态表示状态转移方程初始化和填表顺序返回值提醒 代码实现总结 213. 打家劫舍 II 题目解析 本题是对打家劫舍和按摩师的升级题型&am…...

算法与数据结构之链表
链表的定义,相信大家都知道,这里就不赘述了只是链表分单向链表和双向链表,废话不多说,直接上代码 链表节点的定义: public class Node {int val;Node next;Node pre;public Node(int val, Node next, Node pre) {thi…...

深入剖析React Hooks中的 useCallback
前言 自 React 16.8 版本引入 Hooks 以来,useCallback 成为了前端开发者们越来越青睐的一个功能。useCallback 可以有效优化组件性能,尤其在处理函数式组件中的状态更新时。本文将详细介绍 useCallback 的用法及其注意事项。 1. useCallback 简介 use…...

微服务中配置文件(YAML文件)和项目依赖(POM文件)的区别与联系
实际上涉及到了微服务架构中的两个重要概念:服务间通信和项目依赖管理。在微服务架构中,一个项目可以通过两种方式与另一个项目建立依赖关系:通过配置文件(如YAML文件)和通过项目依赖(如POM文件)…...
Java快速排序算法、三路快排(Java算法和数据结构总结笔记)[7/20]
一、什么是快速排序算法 快速排序的基本思想是选择一个基准元素(通常选择最后一个元素)将数组分割为两部分,一部分小于基准元素,一部分大于基准元素。 然后递归地对两部分进行排序,直到整个数组有序。这个过程通过 par…...

【React】05.JSX语法使用上的细节
水水水水水...

LeetCode 1759. 统计同质子字符串的数目【字符串】1490
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
IDDR)
FPGA UDP RGMII 千兆以太网(2)IDDR
1 xilinx原语 在 7 系列 FPGA 中实现 RGMII 接口需要借助 5 种原语,分别是:IDDR、ODDR、IDELAYE2、ODELAYE2(A7 中没有)、IDELAYCTRL。其中,IDDR和ODDR分别是输入和输出的双边沿寄存器,位于IOB中。IDELAYE2和ODELAYE2,分别用于控制 IO 口输入和输出延时。同时,IDELAYE2 …...

chrome安装vue devtools
不能访问应用商店 如果可以访问应用商店可以往下看 插件源代码 选择shell-chrome,这是官方的插件源码 下载源代码打包 参考教程 点击扩展按钮->管理扩展程序->打开开发者模式->把crx文件拖拽进去即可 可以访问chrome应用商店 插件地址 官方文档地址 选…...
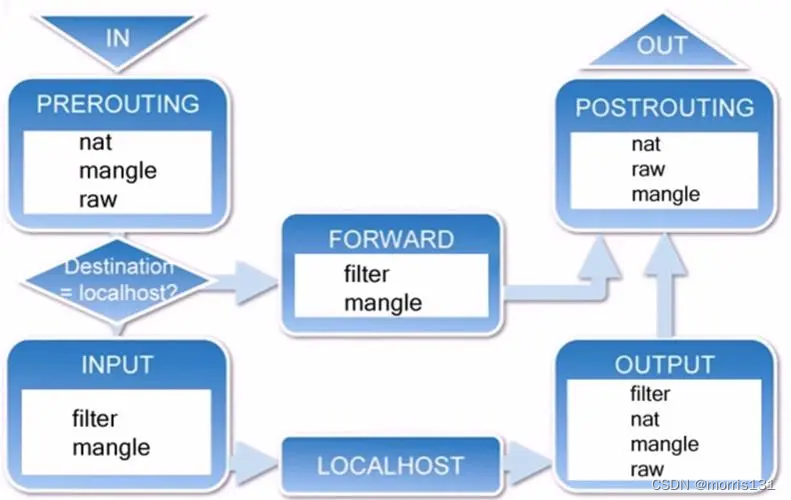
【Docker】iptables命令的使用
iptables是一个非常强大的Linux防火墙工具,你可以使用它来控制网络流量的访问和转发。 前面已经学习了iptables的基本原理,四表五链的基本概念,也已经安装好了iptables,下面我们主要学习iptables命令的基本使用。 可以使用iptable…...

Flex bison 学习好代码
计算机的重要课程编译原理很难学吧, 但是要会用flex &bison的话,容易理解一些。 有些好的项目可以帮助我们,比如 https://github.com/jgarzik/sqlfun 可以帮我们,下载 下来。 在cygwin 下面或者linux 运行: …...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
