力扣370周赛
力扣第370场周赛
找到冠军 I
答案即入度为0的点
class Solution {
public:int findChampion(vector<vector<int>>& grid) {vector<int>d(100+5);int n = grid.size() , m = grid[0].size();for(int i = 0 ; i < n ; i ++){for(int j = 0 ; j < m ; j ++){if(grid[i][j] == true){d[j] ++;}}}for(int i = 0 ; i < n ; i ++){if(d[i] == 0)return i;}return -1;}
};
找到冠军 II
和I相同,加个判断下入度为0的点的个数即可
class Solution {
public:int findChampion(int n, vector<vector<int>>& edges) {vector<int>d(n+5);for(int i = 0 ; i < edges.size(); i ++ ){cout << edges[i][1] << " ";d[edges[i][1]]++;}int res = 0 , cnt = 0;for(int i = 0 ; i < n ; i ++){if(d[i] == 0){res = i;cnt ++;}}if(cnt > 1)return -1;return res;}
};
在树上执行操作以后得到的最大分数
题目可以转化为
在树中选任意节点,使得从根节点出发,到任意叶子节点经过的路径上的节点值之和都不等于0且选的值最小
从根节点开始dfs,选根节点或者子树的和
class Solution {
public:long long maximumScoreAfterOperations(vector<vector<int>>& edges, vector<int>& values) {vector<vector<int>> g(values.size());long long res = 0;for (auto &e: edges) {int x = e[0], y = e[1];g[x].push_back(y);g[y].push_back(x);}function<long long (int , int )> dfs = [&](int u , int f) -> long long {long long ans = values[u] , su = 0;for(auto j:g[u]){if(j == f)continue;su += dfs(j , u);}if(su == 0 || ans < su)return ans;return su;};for(auto x : values)res += x;res -= dfs(0 , -1);return res;}
};
平衡子序列的最大和
1.定义 b[i] = nums[i] - i,问题变成从 b 中选出一个非降子序列,求对应的 nums 的元素和的最大值,离散化后在1e5内
2.定义 f[i] 表示子序列最后一个数的下标是 i 时,对应的 nums 的元素和的最大值。那么答案就是 max(f)
f[i] = max(f[j] , 0) + nums[i];
3.等式左边单点修改,右边区间查询用线段树优化
class Solution {
public:struct Node{int l, r;long long v; // 区间[l, r]中的最大值}tr[400008];void pushup(int u){tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);}void build(int u, int l, int r){tr[u] = {l, r};if (l == r) return;int mid = (l + r) >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pushup(u);}long long query(int u, int l, int r){if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;int mid = (tr[u].l + tr[u].r) >> 1;long long v = 0;if (l <= mid) v = query(u << 1, l, r);if (r > mid) v = max(v, query(u << 1 | 1, l, r));return v;}void modify(int u, int x, long long v){if (tr[u].l == x && tr[u].r == x) tr[u].v = v;else{int mid = (tr[u].l + tr[u].r) >> 1;if (x <= mid) modify(u << 1, x, v);else modify(u << 1 | 1, x, v);pushup(u);}}long long maxBalancedSubsequenceSum(vector<int>& nums) {int n = nums.size();// 离散化 nums[i]-iauto b = nums;for (int i = 0; i < n; i++) {b[i] -= i;}sort(b.begin(), b.end());b.erase(unique(b.begin(), b.end()), b.end()); // 去重build(1, 1, 100001);for (int i = 0; i < n; i++) {// j 为 nums[i]-i 离散化后的值(从 1 开始)int j = lower_bound(b.begin(), b.end(), nums[i] - i) - b.begin() + 1;long long f = max(query(1,0, j), 0LL) + nums[i];modify(1, j, f);}long long res = -0x3f3f3f3f;for(long long x : nums)res = max(res , x);if(query(1,0, 100001) == 0)return res;return query(1,0, 100001); }
};
相关文章:

力扣370周赛
力扣第370场周赛 找到冠军 I 答案即入度为0的点 class Solution { public:int findChampion(vector<vector<int>>& grid) {vector<int>d(1005);int n grid.size() , m grid[0].size();for(int i 0 ; i < n ; i ){for(int j 0 ; j < m ; j )…...

EMNLP2023 | 让模型学会将提示插入到合适的中间层
深度学习自然语言处理 原创作者:cola 现有的提示微调方法基本是人工选择提示层,而人工选择将提示插入到哪些层次并非一定合理,这导致了很大程度上限制提示微调发挥潜能。我们的模型(SPT)可以让模型自己学习应该在哪些中间层插入提示ÿ…...
)
【PG】PostgreSQL单机部署(简洁命令版)
目录 1 下载安装包 2 上传至需要安装的服务器 3 服务器安装所需依赖包 4 解压安装包 5 配置安装 6 创建用户 7 创建目录修改权限 8 设置环境变量 9 设置共享库 10 初始化 11 启动数据库 12 关闭数据库 13 查看数据库状态 14 连接数据库 1 下载安装包 通过下载…...

AI:69-基于深度学习的音乐推荐
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌在这个漫长的过程,中途遇到了不少问题,但是…...

php 使用phpoffice/phpspreadsheet拓展实现导出图片
基础操作参考:https://blog.csdn.net/huaweichenai/article/details/95994006 文档地址:https://phpspreadsheet.readthedocs.io/ github地址:https://github.com/PHPOffice/PhpSpreadsheet 导出插入图片主要使用\PhpOffice\PhpSpreadshee…...
几种解决mfc140.dll文件缺失的方法,电脑提示mfc140.dll怎么办
电脑提示mfc140.dll缺失,如果你不去处理的话,那么你的程序游戏什么都是启动不了的,如果你想知道有什么方法可以解决那么可以参考这篇文章进行解决,今天给大家几种解决mfc140.dll文件缺失的方法。电脑提示mfc140.dll也不用担心解决…...

并发修改异常
并发修改异常(Concurrent Modification Exception)是指在多线程环境下,当一个方法检测到对象的并发修改,但不允许这种修改时,抛出的一种异常。换句话说,当两个或多个线程同时对一个对象进行修改时ÿ…...

split() 函数实现多条件转为数据为数组类型
使用 split() 函数并传递正则表达式 /[,;.-]/ 作为分隔符来将字符串按照逗号、分号和破折号进行拆分,并将结果赋值给 splitArray 数组。下面是一个示例代码: 在上面的示例中,我们使用 split() 函数将 inputString 字符串按照逗号、分号和破折…...

【Springboot】Vue3-Springboot引入JWT实现登录校验以及常见的错误解决方案
文章目录 前言一、JWT简单介绍二、token校验设计思路三、使用步骤Springboot部署JWT引入依赖:创建登录实体类后端:LoginController.java路由守卫函数 四、问题 前言 项目版本: 后端: Springboot 2.7、 Mybatis-plus、Maven 3.8.1…...

VueCli 自定义创建项目及配置
一、VueCli 自定义创建项目 1.安装脚手架 (已安装) npm i vue/cli -g2.创建项目 vue create hm-exp-mobile选项 Vue CLI v5.0.8 ? Please pick a preset:Default ([Vue 3] babel, eslint)Default ([Vue 2] babel, eslint) > Manually select features 选自定义手动…...
)
2024年节假日sql脚本(区分休息日、节假日、工作日、调休工作)
建表 CREATE TABLE no_work_day (id int NOT NULL AUTO_INCREMENT,day varchar(255) DEFAULT NULL,PRIMARY KEY (id) ) ENGINEInnoDB DEFAULT CHARSETutf8mb3 COMMENT节假日表;执行脚本插入数据 INSERT INTO no_work_day (day) VALUES (20240101); INSERT INTO no_work_day (…...
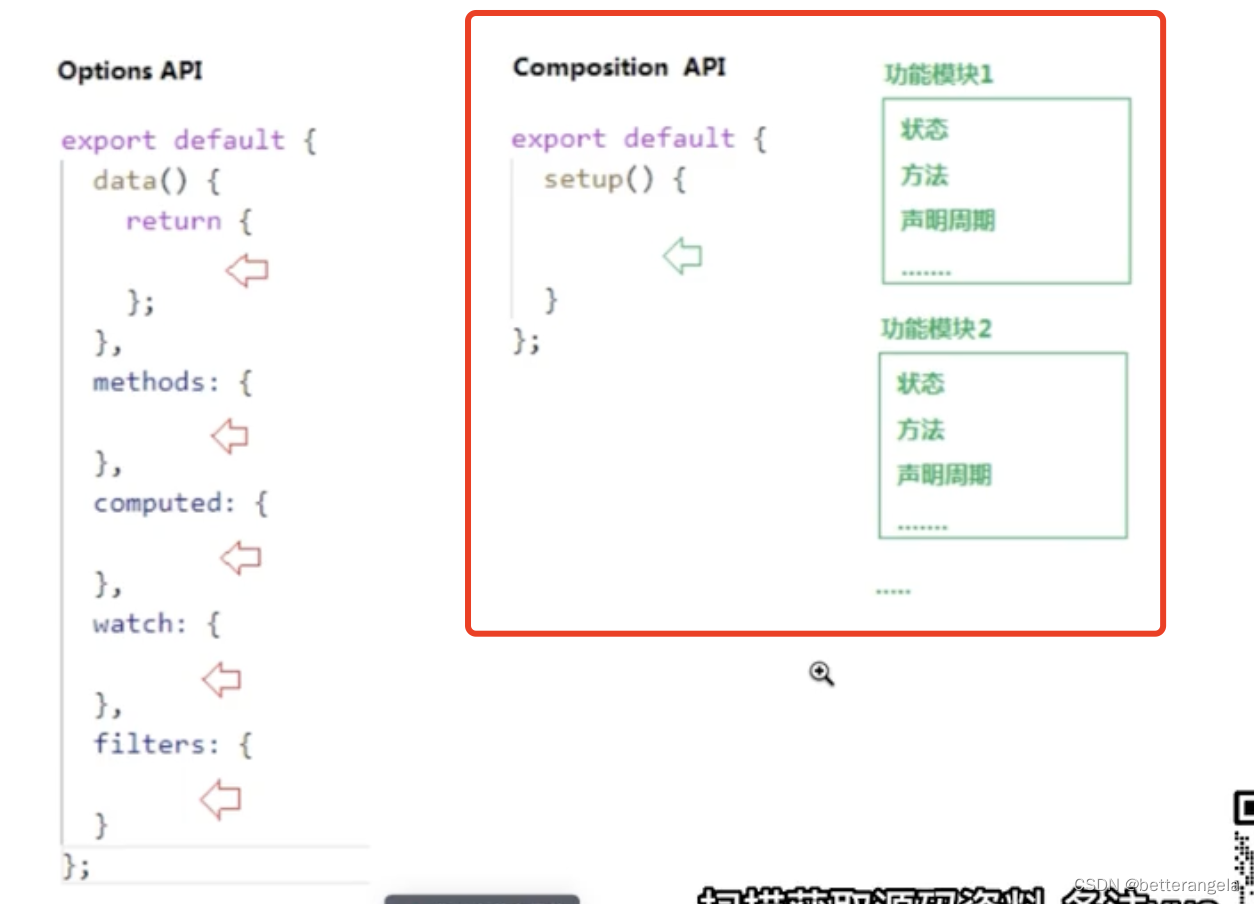
vue3介绍
介绍 3完全兼容2的语法 vue3:体积更小,性能会更高。底层做了很多优化 2倍左右 vue3vitets 渐进式框架 vue3和vue2 的区别 新语法,性能上提升很多 思想是一致的:动态绑定:状态data&计算属性,监听某些状态…...

Spark SQL自定义collect_list分组排序
想要在spark sql中对group by concat_ws()的字段进行排序,可以参考如下方法。 原始数据如下: ------------ |id |name |type| ------------ |1 |name1|p | |2 |name2|p | |3 |name3|p | |1 |x1 |q | |2 |x2 |q | |3 |x3 |q | …...

2023年云计算的发展趋势如何?
混合云的持续发展:混合云指的是将公有云和私有云进行结合,形成一种统一的云计算环境。随着企业对数据隐私和安全性的要求越来越高,以及在数据存储和处理方面的需求不断增长,混合云正在逐渐成为主流。预计未来混合云将会继续保持高…...
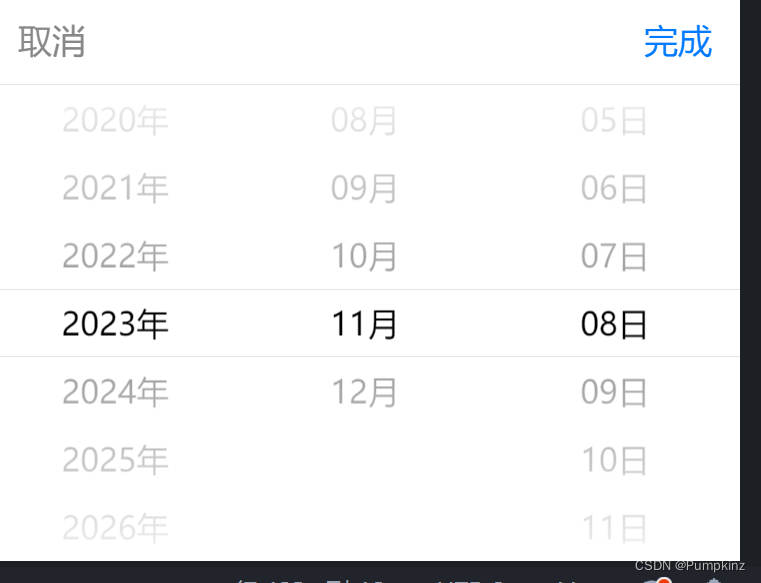
uniapp中picker 获取时间组件如何把年月日改成年月日默认时分秒为00:00:00
如图所示,uniapp中picker组件的日期格式为: 但后端要 2023-11-08 00:00:00格式 如何从2023-11-08转化为 2023-11-08 00:00:00:👇 const date new Date(e.detail.value);//"2023-11-17" date.setHours(0, 0, 0); // 2…...

k8s operator
Kubernetes Operator 是一种用于特定应用的控制器,可扩展 Kubernetes API 的功能,来代表 Kubernetes 用户创建、配置和管理复杂应用的实例。它基于基本 Kubernetes 资源和控制器概念构建,但又涵盖了特定领域或应用的知识,用于实现…...

使用io_uring
目录 升级内核以支持io_uring Io_uring 关注点 有序性 IOPOLL SQPOLL 环大小 wrk线程数量 升级内核以支持io_uring #!/bin/bash#内核源码压缩包 kernel_targz"linux-5.14.21.tar.xz"#内核源码解压后的目录 kernel_source"linux-5.14.21"echo "…...
|LeetCode93. 复原 IP 地址、LeetCode78. 子集、LeetCode90. 子集 II)
LeetCode算法题解(回溯)|LeetCode93. 复原 IP 地址、LeetCode78. 子集、LeetCode90. 子集 II
一、LeetCode93. 复原 IP 地址 题目链接:93. 复原 IP 地址 题目描述: 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 . 分隔。 例如:"0.…...

vue、react数据绑定的区别?
Vue 和 React 是两个流行的前端框架,它们在数据绑定方面有一些区别。 Vue 的数据绑定: Vue 使用双向数据绑定(two-way data binding)的概念。这意味着当数据发生变化时,视图会自动更新;同时,当…...
前端Vue 页面滑动监听 拿到滑动的坐标值
前言 前端Vue 页面滑动监听 拿到滑动的坐标值 实现 Vue2写法 mounted() {// 监听页面滚动事件window.addEventListener("scroll", this.scrolling);}, methods: { scrolling() {// 滚动条距文档顶部的距离let scrollTop window.pageYOffset ||document.documentE…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
