【算法题】最大矩形面积,单调栈解法
力扣:84. 柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。

题意很简单,翻译一下就是:求该图中最大矩形的面积。
那么,这道题的思路就是遍历。不过如何高效遍历是一个学问。
这道题我带来单调栈的解法。
单调栈就是在栈中维护一个单调规律的序列。
这道题,我们可以维护一个单调递增的序列。
遇到该元素比栈顶元素小的情况,就把栈顶元素出栈,直到栈顶元素小于该元素,或该栈为空为止。


为什么要维护一个单调递增的序列呢?
由于序列是递增的所以,最大矩形会非长容易算出最大矩形的面积。

以该矩形为例
以2为高的最大矩形是 2 * 4 = 4;
以3为高的最大矩形是3 * 3 = 9;
以4为高的最大矩形是4 * 2 = 8;
以5为高的最大矩形是5 * 1 = 1;
那么有人要问了,有聪明的小脑管们要问了,哎呀。
实际上某些矩形中间还有矩形,并不是真正的递序列,会不会产生影响捏?
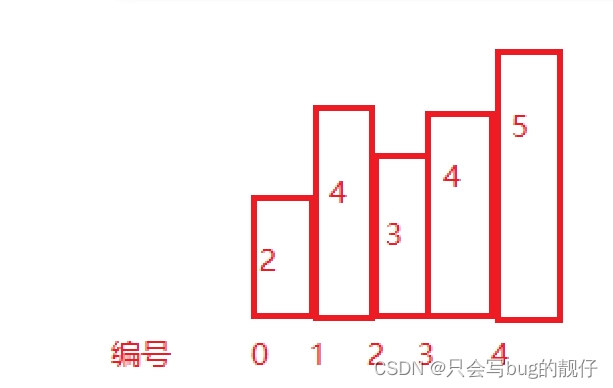
如果原图为这样,那么出栈之后维护的递增图与上图对应。由于中间的4大于3也大于2,所以,中间的矩形应该是最大的,可以把4当成3即可。 我们可以以出栈为契机,计算矩形的面积
以该图我进行解题语言描述:
1: 栈中为空栈,将矩形0入栈。 此时栈中矩形为:0
2: 矩形1的高为4,大于栈顶元素2,将矩形1入栈,此时栈中矩形为 0 ,1
3:矩形2的高为3,3小于栈顶元素的高4,所以将栈顶矩形1出栈,同时计算矩形1高的最大
矩形,为 4 * 1 = 4;同时将3入栈,此时栈中矩形为: 0, 2
4:因为矩形3的高大于栈顶矩形2的高,所以将矩形3入栈,此时栈中矩形为: 0, 2,3
5:因为矩形4的高大于栈顶矩形3的高,所以将矩形4入栈,此时栈中矩形为: 0, 2,3,4
6.此时所有的元素已经入栈完毕,且栈中元素为地址矩形,依次出栈计算所有值即可,最重要的出栈,即出栈到3的时候,不能直接拿4矩形序号减去2徐行序号 + 1,因为2号矩形前面可能还有徐行,应该捡到0矩形之后,2矩形之前。
JAVA代码的实现
class Solution {public int largestRectangleArea(int[] heights) {int maxS = 0;Stack<Integer> st = new Stack<>();//添加矩形入栈for(int i = 0; i < heights.length; i++){if(st.empty() || heights[i] >= heights[st.peek()]){st.push(i);}else{while(!st.empty() && heights[st.peek()] > heights[i]){int tempH2 = heights[st.pop()];if(st.empty()){maxS = Math.max(tempH2 * i,maxS);break;}else {}maxS = Math.max(maxS, (i - st.peek() - 1) * tempH2);}st.push(i);}}//添加完毕,依次出栈if(!st.empty()){int tempH = heights[st.peek()];int tempI = st.pop();if (st.empty()){maxS = Math.max(maxS, tempH);return maxS;}else {maxS = Math.max(maxS, tempH * (tempI - st.peek()));}while(!st.empty()){int tempH2 = heights[st.pop()];if(st.empty()){maxS = Math.max(tempH2 * (tempI + 1),maxS);break;}maxS = Math.max(maxS, (tempI - st.peek()) * tempH2);}}return maxS;}
}
同时该题也有一种取巧的做法,在守卫补两个高度为0的矩形,不影响结果的情况下,可以将流程统计, 即压入最右面的0的时候吧所有的矩形都出栈,所有矩形将出栈完毕,即计算完毕。
JAVA代码实现
public int largestRectangleArea(int[] heights) {int res =0 ;int n = heights.length;int[] arr = new int[n+2];//复制数组,首位加0System.arraycopy(heights,0,arr,1,n);Deque<Integer> stack = new ArrayDeque<>();int nOfArr = arr.length;arr[0] = arr[nOfArr-1] = 0;//依次比较入栈for (int i = 0; i < nOfArr; i++) {int h = arr[i];while (!stack.isEmpty() && h < arr[stack.peek()]){int tmph = arr[stack.pop()];res = Math.max(res,tmph * (i - stack.peek() - 1));}stack.push(i);}return res;}
相关文章:

【算法题】最大矩形面积,单调栈解法
力扣:84. 柱状图中最大的矩形 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。 题意很简单,翻译一下就是:求该图中…...

活动策划|深度分析年货节活动该如何策划!
四月初,不平凡的初春开始恢复往日的平静。对于新零售行业,疫情的缓解也逐渐平稳生态链的运转。2020年新零售的格局在洗礼后,业务的聚焦点也从前端促销转移到后端履约的体验闭环,同时很大程度的推进企业在危机公关下的应对。618大促…...

Idea启动遇到 Web server failed to start. Port 8080 was already in use. 报错
Idea启动遇到问题-记录 报错英文提示: APPLICATION FAILED TO START Description: Web server failed to start. Port 8080 was already in use. Action: Identify and stop the process that’s listening on port 8080 or configure this application to liste…...
函数知识点总结)
Python3中zip()函数知识点总结
1.引言 在本文中,我将带领大家深入了解Python中的zip()函数,使用它可以提升大家的工作效率。 闲话少说,我们直接开始吧! 2. 基础知识 首先,我们来介绍一些基础知识点: Python中的某些数据类型是不可变的…...

过滤器,监听器,拦截器的原理与在Servlet和Spring的应用
在Java Web的开发中,最原始和初期的学习都是从Servlet开始的,Servlet是Java最为耀眼的技术,也是Java EE的技术变革。目前大火主流的框架spring boot也的spring mvc部分也是基于拓展servlet完成的。回到之前的文章spring 实现了对servlet的封装…...

minio spring boot 秒传、分片上传、断点续传文件实现
此处后端使用的是前期封装的自定义starter,具体链接可参考:minio对象存储spring boot starter封装组件 这里主要针对前期封装的组件,做一个简单的应用,前端直传可查看之前的文章 秒传 秒传的逻辑比较简单,在前传上传…...

MTK平台使用Omnipeek分析空口协议讲解
讲解这个之前,我们先来了解下beacon/robe Request/Probe Response 三种帧 beacon帧 信标帧,由AP以一定的时间间隔周期性发出,以此来告诉外界自己无线网络的存在。 Beacon帧作为802.11中一个周期性的帧,Beacon周期调高,对应睡眠周期拉长,故节能(即越来休息100ms再起来…...
string和自动推断类型
欢迎来观看温柔了岁月.c的博客目前设有C学习专栏C语言项目专栏数据结构与算法专栏目前主要更新C学习专栏,C语言项目专栏不定时更新待C专栏完毕,会陆续更新C项目专栏和数据结构与算法专栏一周主要三更,星期三,星期五,星…...
【软件测试】从功能到自动化测试,测试人的进阶之路细节,这些必不可少......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 测试流程࿰…...
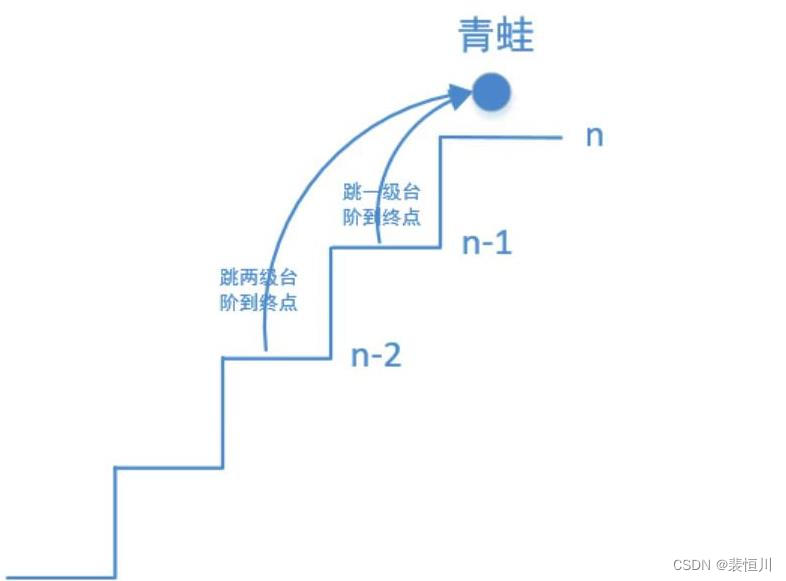
C语言青蛙跳台阶【图文详解】
青蛙跳台阶前言1. 题目介绍2. 解题思路3. 利用图片来演示青蛙跳台阶的原理4. 如何用C语言实现青蛙跳台阶前言 在本文,我们要与一只活泼可爱的小青蛙合作,带领着它跳上台阶,这个小家伙精力充沛,特别擅长于跳跃。我们要让它做我们的…...
——list容器的基础理论知识)
笔记(五)——list容器的基础理论知识
list容器是一个双向链表容器,可以高效地进行插入删除元素,但是不能随机存取元素(不支持at()和[]操作符)。一、list容器的对象构造方法list对象采用模板类的默认构造形式例如list<T> lst;#include<iostream>…...

浅谈网络中接口幂等性设计问题
所谓幂等性设计,就是说,一次和多次请求某一个资源应该具有同样的副作用。用数学的语言来表达就是:f(x) f(f(x))。 在数学里,幂等有两种主要的定义。 在某二元运算下,幂等元素是指被自己重复运算(或对于函数…...
《C Primer Plus》第13章复习题与编程练习
《C Primer Plus》第13章复习题与编程练习复习题1. 下面的程序有什么问题?2. 下面的程序完成什么任务?(假设在命令行环境中运行)3. 假设程序中有下列语句:4. 编写一个程序,不接受任何命令行参数或接受一个命…...

计算机SCI论文应该怎么作图? - 易智编译EaseEditing
计算机SCI论文,作图时要注意以下几个方面的问题: 1.图片的格式要tiff或者eps; 2.文件大小不能超过10M; 3.长和宽也给出了具体要求; 4.色彩模式要RGB或者灰度图; 5.文中的文字字体和大小; …...
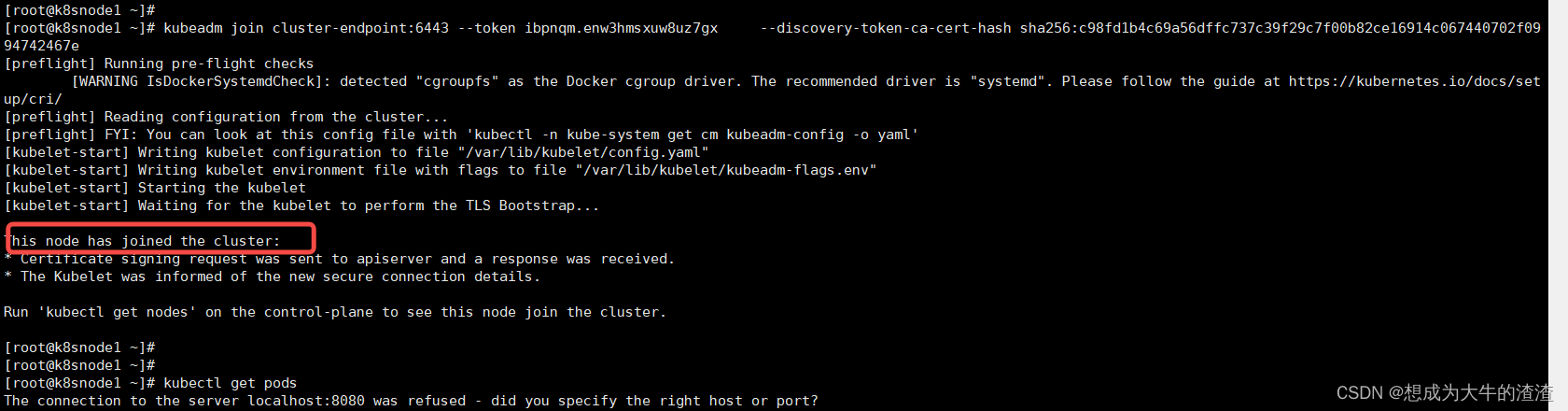
【一】kubernetes集群部署
一、docker环境搭建 1、移除以前docker相关包 sudo yum remove docker docker-client docker-client-latest docker-common docker-latest docker-latest-logrotate docker-logrotate docker-engine2、配置yam源 sudo yum install -y yum-utilssudo yum-config-manager --ad…...

Docker安装Redis
一、拉取镜像 命令::docker pull <镜像名称>:<版本号> docker pull redis 二:Docker挂载配置文件 挂载:即将宿主的文件和容器内部目录相关联,相互绑定,在宿主机内修改文件的话也随之修改容…...
 系统执行的过程)
在shell中执行一条可执行程序(./a.out) 系统执行的过程
目录 系统调度过程 用户空间角度: 内核角度 1、调用fork创建一个新进程 2、使用_fo_fork创建新进程 3、父进程调用wake_up_new_task尝试唤醒新进程 4、CPU选择一个合适的进程来运行; 5、运行新进程 6、实现负载均衡 系统调度过程 分析在命令行…...
【ArcGIS Pro二次开发】(10):属性表字段(field)的修改
在ArcGIS Pro中,经常会遇到用字段计算器对要素的属性表进行计算。下面以一个例子演示如何在ArcGIS Pro SDK二次开发中实现。 一、要实现的功能 如上图所示的要素图层,要实现如下功能: 当字段【市级行政区】的值为【泉州市】时,将…...

数据结构与算法—散列表
目录 散列表 散列函数 散列冲突解决 1、开放寻址法 1.1 线性探测 1.2 二次探测 1.3 双重散列 2、链表法 使用场景 单词查找 散列表与链表的结合使用LRU 散列表总结 散列表实例 散列表 Word 单词拼写功能,如何实现的?散列表(Has…...

计算机网络笔记、面试八股(一)—— TCP/IP网络模型
本章目录1. TCP/IP网络模型1.1 应用层1.1.1 应用层作用1.1.2 应用层有哪些常用协议1.2 运输层1.2.1 TCP与UDP的区别1.2.2 分块传输1.2.3 端口1.3 网络层1.3.1 IP报文1.3.2 IP地址1.3.3 网络号和主机号的获得1.3.4 子网掩码的获得1.3.5 路由1.3.6 IP地址与MAC地址的区别1.3.7 AR…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
