【力扣:1504】统计全1子矩阵
统计全1子矩阵个数
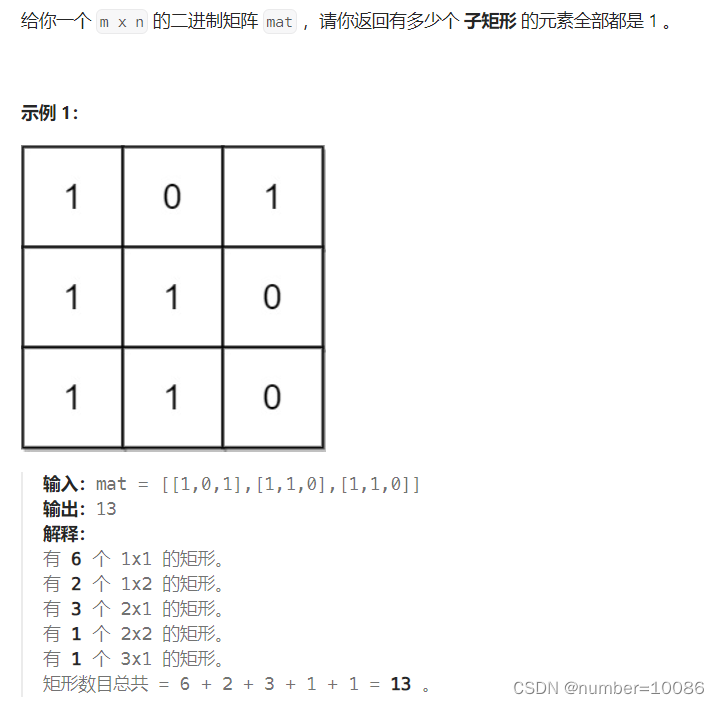
思路1:首先考虑深度优先模拟,从【0,0】出发向下、右扩展,符合条件res++,最后输出res,比较直观,但重复进行了大量节点遍历操作,时间复杂度较高,数据量大时会超时
class Solution {unordered_set<int>set;int res=0;void get(vector<vector<int>>& mat,int start_r,int start_c,int row,int col){if(row>=mat.size()||col>=mat[0].size()||set.count(start_r+(start_c+((row+col*151)*151))*151)) return;for(int i=start_r;i<=row;i++){if(!mat[i][col]) return;}for(int i=start_c;i<=col;i++){if(!mat[row][i]) return;}res++;set.insert(start_r+(start_c+((row+col*151)*151))*151);get(mat,start_r,start_c,row+1,col);get(mat,start_r,start_c,row,col+1);}
public:int numSubmat(vector<vector<int>>& mat) {for(int i=0;i<mat.size();i++){for(int j=0;j<mat[0].size();j++){get(mat,i,j,i,j);}}return res;}
};
思路2:单考虑行或列时每增加1个1,结果增加 行或列1个数+1,那么多行多列时每增加一行或一列增加(1+2+…+n)*(m+1),加列时:n为行数,m为原来列数,实际上情景就是第一个图的拓展,只不过矩形中的1实际上是长度相等的全1矩形
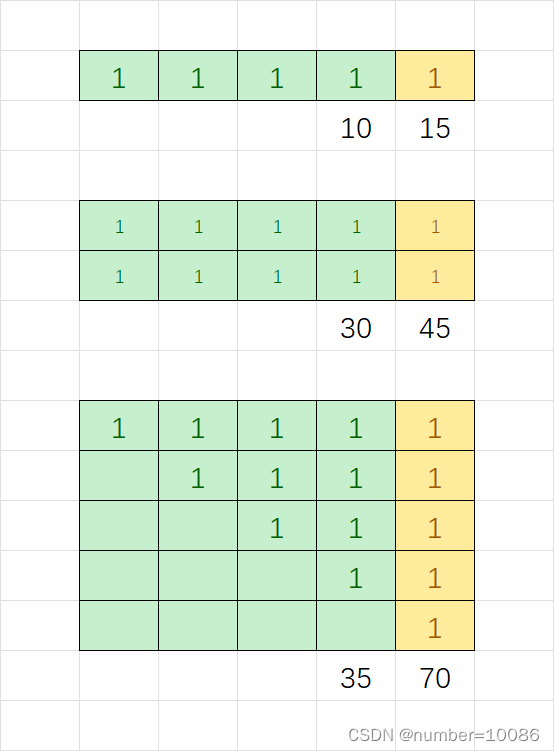
因而仅需要使用一个二维数组tmp存储target[i][j]及前有几个连续的1,然后从上到下加上min(tmp[i][j],tmp_pre_min)即可
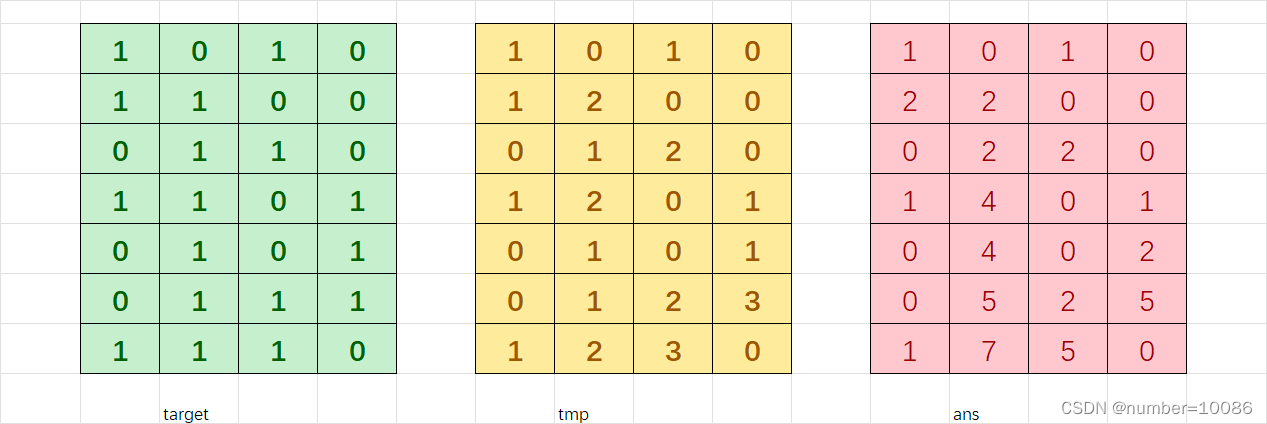
class Solution {
public:int numSubmat(vector<vector<int>>& mat) {int n = mat.size();int m = mat[0].size();vector<vector<int> > row(n, vector<int>(m, 0));for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (j == 0) {row[i][j] = mat[i][j];} else if (mat[i][j]) {row[i][j] = row[i][j - 1] + 1;}else {row[i][j] = 0;}}}int ans = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {int col = row[i][j];for (int k = i; k >= 0 && col; --k) {col = min(col, row[k][j]);ans += col;}}}return ans;}
};
单调栈优化后代码:
class Solution {
public:int numSubmat(vector<vector<int>>& mat) {int n = mat.size();int m = mat[0].size();vector<vector<int> > row(n, vector<int>(m, 0));for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (j == 0) {row[i][j] = mat[i][j];} else if (mat[i][j]) {row[i][j] = row[i][j - 1] + 1;}else {row[i][j] = 0;}}}int ans = 0;for (int j = 0; j < m; ++j) { int i = 0; stack<pair<int, int> > Q; int sum = 0; while (i <= n - 1) { int height = 1; while (!Q.empty() && Q.top().first > row[i][j]) {// 弹出的时候要减去多于的答案sum -= Q.top().second * (Q.top().first - row[i][j]); height += Q.top().second; Q.pop(); } sum += row[i][j]; ans += sum; Q.push({ row[i][j], height }); i++; } } return ans;}
};
相关文章:

【力扣:1504】统计全1子矩阵
统计全1子矩阵个数 思路1:首先考虑深度优先模拟,从【0,0】出发向下、右扩展,符合条件res,最后输出res,比较直观,但重复进行了大量节点遍历操作,时间复杂度较高,数据量大时…...

排序算法之-选择
算法原理 在未排序的数列中找出最大(或最小)的元素,然后将其存入到已排序的数列起始位置,紧接着在剩余的未排序数列中继续查找最大(或最小)的元素,并将其放入到已排序的数列末尾,依…...

机器学习模板代码(期末考试复习)自用存档
机器学习复习代码 利用sklearn实现knn import numpy as np import pandas as pd from sklearn.neighbors import KNeighborsClassifier from sklearn.model_selection import GridSearchCVdef model_selection(x_train, y_train):## 第一个是网格搜索## p是选择查找方式:1是欧…...

使用sizeof()和strlen()去计算【数组】和【指针】的大小
文章目录 一、知识回顾1、回顾sizeof()、strlen的作用:2、数组和指针3、数组名 二、sizeof()、strlen()的使用区别1、注意区别:2、一维数组与一级指针3、二维数组与二级指针 三、总结回顾 一、知识回顾 1、回顾sizeof()、strlen的作用: siz…...
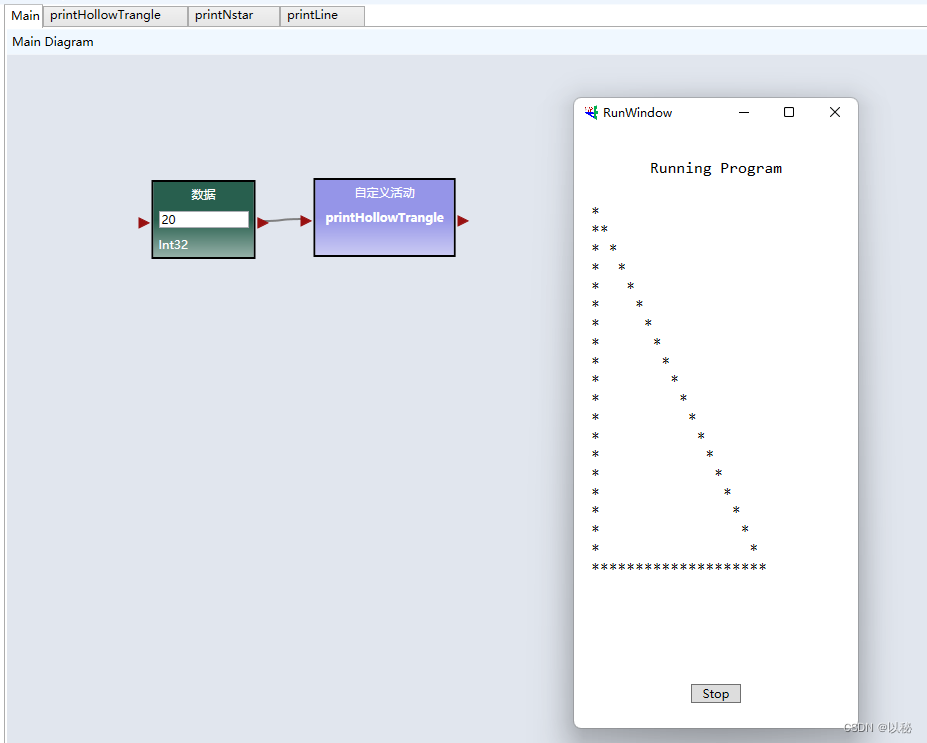
viple进阶4:打印空心三角形
题目:根据用户输入的行数n打印空心三角形,下图分别为n3、n4、n5和n10的效果图 第一步:观察效果图 输入的行数为3,打印结果就有3行;输入的行数为4,则打印结果就有4行;以此类推,输入的…...

Oauth2.0的内容
OAuth 2.0是一个授权协议,用于允许第三方应用程序访问用户在另一个应用程序上存储的受保护资源,而不需要将用户名或密码公开给第三方应用程序。 OAuth2.0基于客户端-服务器模型,通常需要三个主体:客户端、资源所有者和授权服务器…...
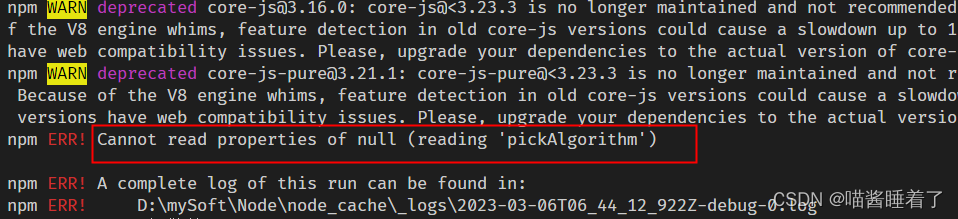
npm 下载包失败解决方案
1.【问题描述】使用 npm 下载vue项目依赖包时失败,版本不一致。 【解决方法】使用 npm install --force npm install --force 是一个命令行指令,用于在 Node.js 环境中使用 npm(Node Package Manager)安装包或模块。–force 参数表…...

C语言---插入排序、希尔排序、冒泡排序、选择排序、快速排序简单介绍
文章目录 插入排序希尔排序冒泡排序选择排序快速排序 本文主要介绍用C语言实现的一些排序方法,有插入排序、希尔排序、冒泡排序、选择排序和快速排序,文章中给出的例子都是按照升序排列的。 插入排序 若数组只有一个元素,自然不用排序&#…...

撸视频号收益这个副业靠谱吗?
我是卢松松,点点上面的头像,欢迎关注我哦! 昨天有个人问我说做视频号能月入过万吗? 我的回复是:99%的人不能。 但为什么会经常有人这么问呢,松松思考了一下,原因是最近很多人在晒视频号撸收益的项目&am…...

2、数组、Map+HashMap、Set+Hashset、Char和Character类、String类和Char类、Math类
数组 \\一个普通的长度为1的整数数组 Integer[] arr new Integer[1];\\一个普通长度为1的同时元素初始化为1的整数数组。 Integer[] arr new Integer[]{1};\\一个长度为0的空数组 Integer[] arr new Integer[0];Map 常见方法 void clear( ) 从此映射中移除所有映射关系&#…...

ESP8266 WiFi模块快速入门指南
ESP8266是一种低成本、小巧而功能强大的WiFi模块,非常适合于物联网和嵌入式系统应用。本指南将为您提供关于ESP8266 WiFi模块的快速入门步骤和基本知识。 第一步:硬件准备 首先,您需要将ESP8266 WiFi模块与您的开发板连接。通常情况下&#…...
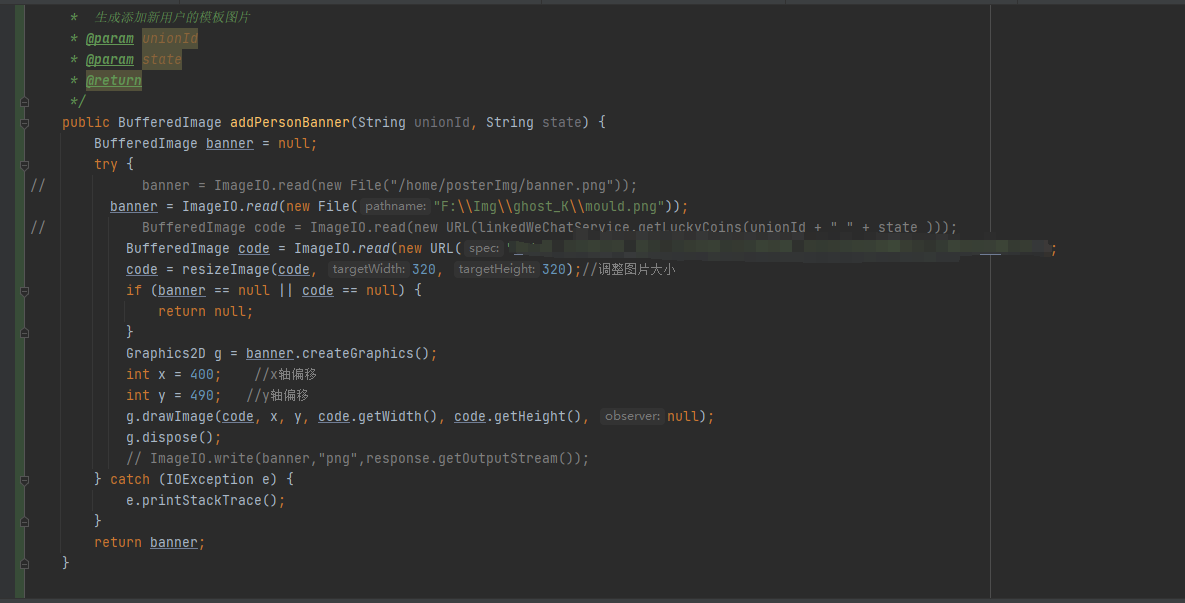
微信小程序将后端返回的图片文件流解析显示到页面
说明 由于请求接口后端返回的图片格式不是一个完整的url,也不是其他直接能显示的图片格式,是一张图片 后端根据模板与二维码生成图片,返回二进制数据 返回为文件流的格式,用wx.request请求的时候,就自动解码成为了下面这样的数据数据格式,这样的数据没…...
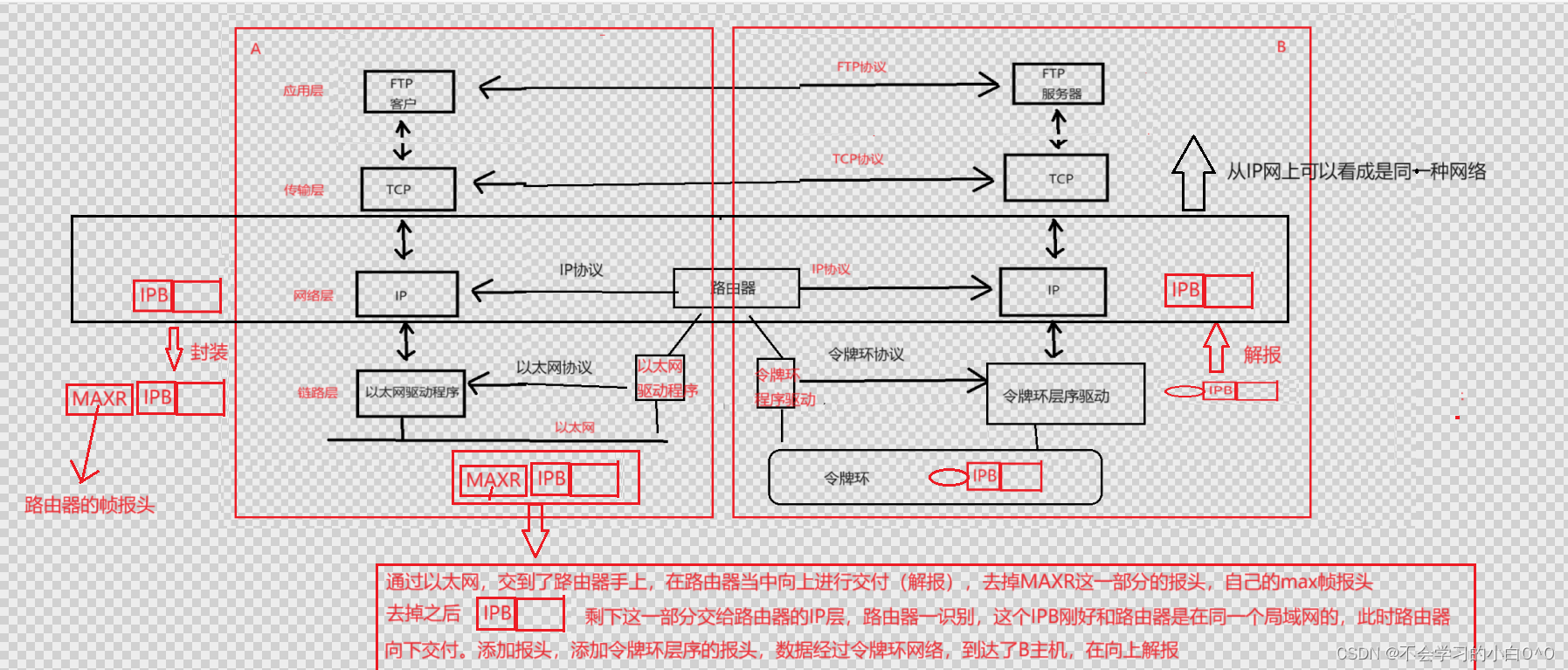
网络基础(1)
目录: 1.了解局域网(LAN)和广域网(WAN) 2.认识“协议” 3.浅谈OSI七层模型 4.网络传输的基本流程 5.路由器这个设备 ---------------------------------------------------------------------------------------…...

flink的AggregateFunction,merge方法作用范围
背景 AggregateFunction接口是我们经常用的窗口聚合函数,其中有一个merge方法,我们一般情况下也是实现了的,但是你知道吗,其实这个方法只有在你使用会话窗口需要进行窗口合并的时候才需要实现 AggregateFunction.merge方法调用时…...
Day25力扣打卡
打卡记录 寻找旋转排序数组中的最小值(二分) 链接 由于是旋转排序数组,所以整个数组有两部分是递增的,选取右侧最后元素,即可将整个数组分为大于该元素和小于该元素,碰头地段即为最小值。 class Solutio…...

SpringCloud - OpenFeign 参数传递和响应处理(全网最详细)
目录 一、OpenFeign 参数传递和响应处理 1.1、feign 客户端参数传递 1.1.1、零散类型参数传递 1. 例如 querystring 方式传参 2. 例如路径方式传参 1.1.2、对象参数传递 1. 对象参数传递案例 1.1.3、数组参数传递 1. 数组传参案例 1.1.4、集合类型的参数传递…...

Postgresql数据类型-布尔类型
前面介绍了PostgreSQL支持的数字类型、字符类型、时间日期类型,这些数据类型是关系型数据库的常规数据类型,此外PostgreSQL还支持很多非常规数据类型,比如布尔类型、网络地址类型、数组类型、范围类型、json/jsonb类型等,从这一节…...

SPASS-交叉表分析
导入数据 修改变量测量类型 分析->描述统计->交叉表 表中显示行、列变量通过卡方检验给出的独立性检验结果。共使用了三种检验方法。上表各种检验方法显著水平sig.都远远小于0.05,所以有理由拒绝实验准备与评价结果是独立的假设,即认为实验准备这个评价指标是…...

用Python的requests库来模拟爬取地图商铺信息
由于谷歌地图抓取商铺信息涉及到API使用和反爬虫策略,直接爬取可能会遇到限制。但是,我们可以使用Python的requests库来模拟爬取某个网页,然后通过正则表达式或其他文本处理方法来提取商铺信息。以下是一个简单的示例: # 导入requ…...

使用EvoMap/Three.js模拟无人机灯光秀
一、创建地图对象 首先我们需要创建一个EM.Map对象,该对象代表了一个地图实例,并设置id为"map"的文档元素作为地图的容器。 let map new EM.Map("map",{zoom:22.14,center:[8.02528, -29.27638, 0],pitch:71.507,roll:2.01,maxPit…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
