混沌系统在图像加密中的应用(小波混沌神经网络)
混沌系统在图像加密中的应用(小波混沌神经网络)
- 前言
- 一、小波混沌神经网络模型
- 二、拓展
- 三、python代码
前言
小波混沌神经网络是一种神经网络模型,结合了小波变换和混沌理论,用于信号处理、分类和预测。该模型基于多层前向神经网络,其中每一层由小波基函数和一个非线性混沌函数构成。
一、小波混沌神经网络模型
选用由小波函数组成的小波暂态混沌神经网络作为研究对象。在连续Hopfield网络中引入小波理论和暂态混沌构造的小波混沌神经网络定义如下
对于Hopfield网络可以看我之前的文章
混沌系统在图像加密中的应用(Hopfield混沌神经网络)

与 Hopfield 神经网络相 比,此小波混沌神经网络的激励函数由小波函数和 Sigmoid 函数组成,且具有暂态的混沌动力学行为。其激励函数是非单调递增但总体上是递增的函数,是由 Sigmoid 函数和 Wavelet 函数组合而成的。
Wavelet 函数的意义是既能使激励函数非单调,又能使激励函数有小波函数的优点。其混沌产生机制是通过自反馈连接项按指数方式递减引入的。且此网络多增加了一项非线性时变衰减项

当自反馈连接权 z(t) 以指数方式趋于零时,此混沌神经网络退化为一个 Hopfield 神经网络
为了更好地分析上述模型的运行机理,以单个神经元为例(令α=0),分析混沌 Hopfield 神经网络的动力学特性。我们选取的激活函数为sigmoid + Wavelet 函数,设置网络参数分别为:
ε_1 = 0.035
ε_2 = 0.1
c = 1/7
k = 1.0
u_0 = 0.5
z_0 = 0.8
I_0 = 0.6
β = 0.001
则网络的输出 v(t)、退温函数z(t)的演化过程分别如下图所示。由图,该网络具有暂态混沌动力学行为,随 着z(t) 不断衰减,通过一个倍周期逆分岔的连续混沌分岔过程,网络将逐渐趋近于一个稳定的平衡点。


二、拓展
大家可以试试其他激活函数,比如softPlus、arcTan、softsign、bent_identity、symmetrical_sigmoid、log_log、gauss、Morlet、ReLU、P-ReLU、Leaky-ReLU、Maxout 等等
三、python代码
import numpy as np
import matplotlib.pyplot as plt
import pylab as mpl
mpl.rcParams['font.sans-serif'] = ['YouYuan'] # 指定默认字体def sigmoid(x):return 1. / (1 + np.exp(-x))
def Morlet(x):return np.exp(-((x)**2) / 2) * np.cos(5 * x)
def Wave(u_t0, z0):v_t = sigmoid((u_t0 / r1)) + c * Morlet((u_t0 / r2))u_t = k * u_t0 - z0 * (v_t - I0)z_t = (1 - b) * z0return v_t, u_t, z_tlist_vt = []
list_ut = []
list_I0 = []
list_zt = []
list_rt = []
list_time = []
# 系统初值
z0 = 0.8
u_t0 = 0.5
# 系统参数
r1 = 0.035
r2 = 0.1
c = 1 / 7 # 0<c<1
k = 1.0 # 0<=k<=1
b = 0.001 # 0<b<1
I0 = 0.60
for i in range(1500):v_t1, u_t1, z1 = Wave(u_t0, z0)u_t0 = u_t1z0 = z1r0 = r1list_vt.append(v_t1)list_I0.append(I0)list_ut.append(u_t0)list_zt.append(z0)list_rt.append(r0)list_time.append(i)plt.figure()
plt.title('Wave Chaos -- activation:sigmoid+Morlet')
plt.tick_params(labelsize=15)
plt.xlabel('迭代次数', fontsize=15)
plt.ylabel('v(t)', fontsize=15)
plt.grid(True, color='c', linestyle='--', linewidth='1')
plt.scatter(list_time, list_vt, c='r', marker='.', s=1)plt.figure()
plt.tick_params(labelsize=15)
plt.xlabel('迭代次数', fontsize=15)
plt.ylabel('z(t)', fontsize=15)
plt.grid(True, color='c',linestyle='--',linewidth='1')
plt.scatter(list_time, list_zt, c='r',marker='.', s=1)plt.show()
相关文章:

混沌系统在图像加密中的应用(小波混沌神经网络)
混沌系统在图像加密中的应用(小波混沌神经网络) 前言一、小波混沌神经网络模型二、拓展三、python代码 前言 小波混沌神经网络是一种神经网络模型,结合了小波变换和混沌理论,用于信号处理、分类和预测。该模型基于多层前向神经网…...

Node.js中的文件系统(file system)模块
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

react组件间通信之context
一般用于【祖组件】与【后代组件】间通信 案例: A,B,C,D四个组件的关系分别为:爷爷,爸爸,儿子,孙子 从A向C传递参数:C组件为类式组件 从A向D传递参数:D组件为函数组件 import React, { Componen…...

京东数据分析:2023年10月京东洗衣机行业品牌销售排行榜
鲸参谋监测的京东平台10月份洗衣机市场销售数据已出炉! 10月份,洗衣机市场整体销售呈上升走势。鲸参谋数据显示,今年10月,京东平台洗衣机市场的销量为143万,环比增长约23%,同比增长约1%;销售额约…...
QQ恢复聊天记录,就用这3个方法!
无论是因为误操作、手机丢失、系统崩溃,还是因为更换了新手机,恢复重要的QQ聊天记录都是一件必做的事情。通过聊天记录,用户可以随时查看之前的信息,以便了解事情的经过。 那么,如何恢复丢失的QQ聊天记录呢࿱…...

高能数造电池3D打印智能制造小试线,开启全固态电池数字化新时代
在科技创新的浪潮中,电池制造领域又迎来了一次突破性的进展。近日,高能数造(西安)技术有限公司重磅推出了其最新电池数字制造装备——全固态电池3D打印智能制造小试线 ,这一创新性的技术开启了全固态电池的数字化智造新时代,为全固…...

stable diffusion为什么能用于文本到图像的生成
推荐基于稳定扩散(stable diffusion) AI 模型开发的自动纹理工具: DreamTexture.js自动纹理化开发包 - NSDT 稳定扩散获得如此多关注的原因 如果你还没有看过它:稳定扩散是一个文本到图像的生成模型,你可以输入一个文本提示,比如…...
c语言刷题第10周(16~20)
规律: 若多个次数最多按ASCII码顺序输出。 用for循环i取(0~26) 则输出满足条件的字符串中位置最靠前的那个。 用while循环遍历(while(a[i]!\0)) 从键盘输入任意只含有大小写字母的串s&…...

Vue.js 响应式系统深度剖析
Vue.js 是当前最流行的 JavaScript 前端框架之一,其核心特性之一就是响应式系统。Vue.js 响应式系统的设计允许开发者以声明式的方式更新 DOM,随着数据变化自动更新相关组件。本文将详细介绍 Vue.js 响应式系统的工作原理,并通过示例来展示其…...
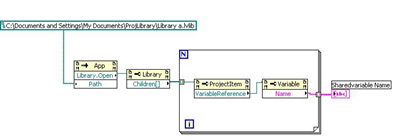
LabVIEW如何才能得到共享变量的引用
LabVIEW如何才能得到共享变量的引用 有一个LabVIEW 库文件 (.lvlib) ,其中有一些定义好的共享变量。但需要得到每个共享变量的引用以便在程序运行时访问其属性。 共享变量的属性定义在“变量”类属性节点中。为了访问变量类,共享变量的引用必须连接到变…...
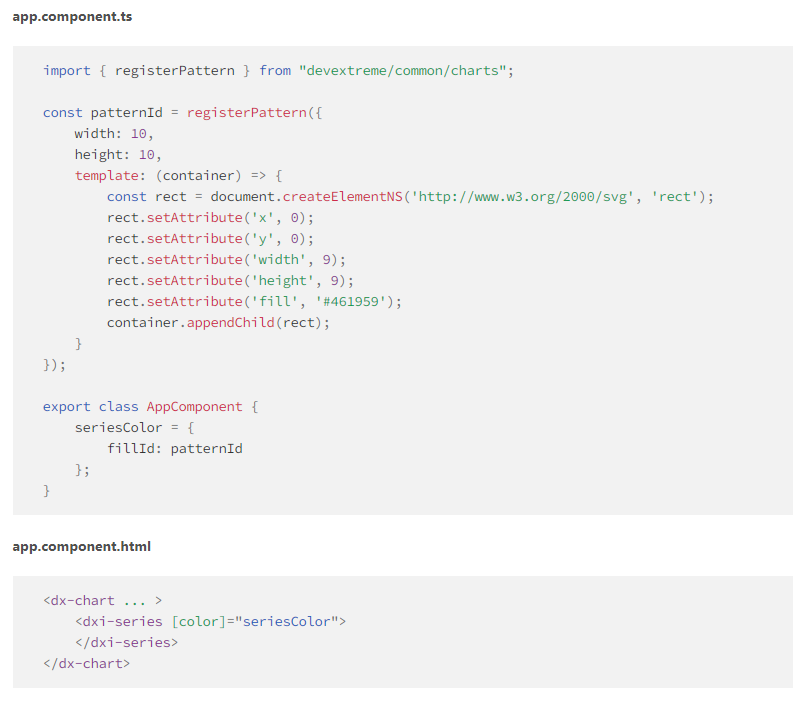
界面控件DevExtreme图表和仪表(v23.1) - 新功能(Angular,React,Vue,jQuery)
本文将为大家总结下DevExtreme在v23.1版本中发布的一些与图表和仪表盘相关的功能。 DevExtreme拥有高性能的HTML5 / JavaScript小部件集合,使您可以利用现代Web开发堆栈(包括React,Angular,ASP.NET Core,jQuery&#…...

Rust和isahc库编写代码示例
Rust和isahc库编写的图像爬虫程序的代码: rust use isahc::{Client, Response}; fn main() { let client Client::new() .with_proxy("") .finish(); let url ""; let response client.get(url) .send() …...
Win10笔记本开热点后电脑断网的解决方法
在Win10笔记本电脑中用户可以随时打开热点,但是发现热点开启后电脑就会断网,网络不稳定就会影响到用户的正常使用。下面小编给大家介绍两种简单的解决方法,解决后用户在Win10笔记本电脑开热点就不会有断网的问题出现了。 具体解决方法如下&am…...
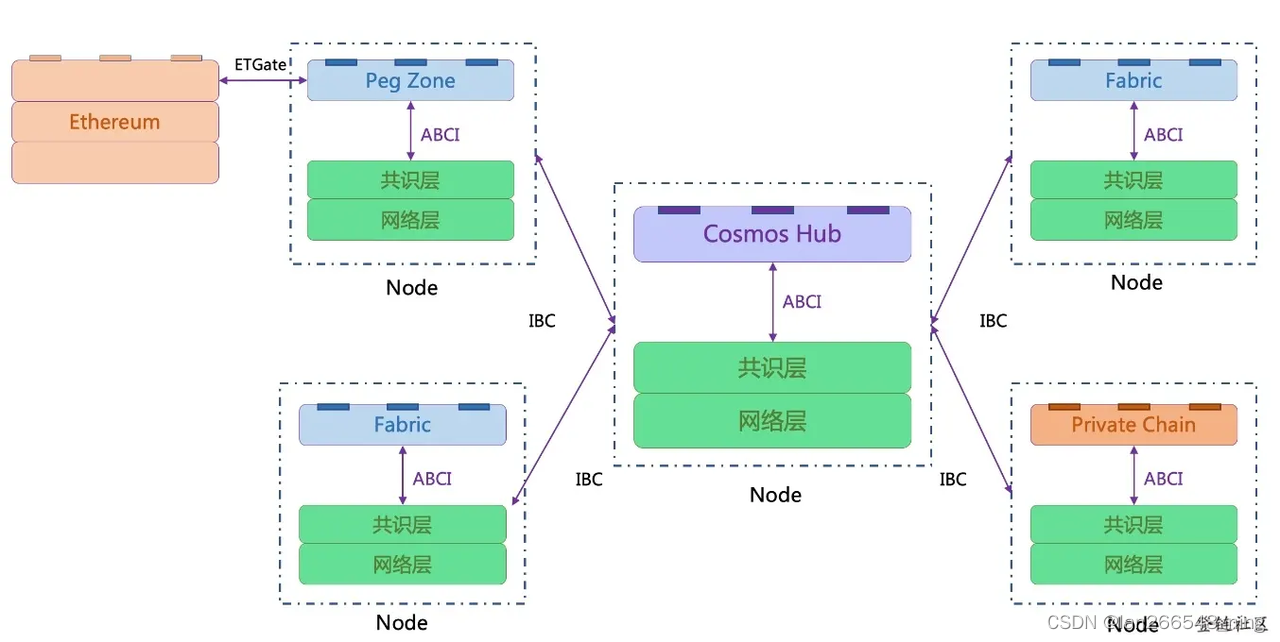
跨链知识指南
跨链知识指南 什么是跨链 跨链就是能够让两个不同的链产生某种关联的技术,或者说能把链A的东西搬到链B,跨链是一个复杂的过程,需要链对链外的信息的获取与验证,需要节点有单独的验证能力等等 什么是跨链桥? 跨链桥…...
字符编码转换时发生内存越界引发的摄像头切换失败问题的排查
目录 1、问题说明 2、初步分析 3、字符串字符编码说明 4、进一步分析 5、为啥在日常测试时没有遇到切换摄像头失败的问题呢? 6、华为MateBook笔记本使用高通的CPU 7、最后 VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更…...

git修改之前的commit提交的作者信息和邮箱信息
更改之前提交的作者信息和邮箱信息需要进行两步操作。首先,使用 git filter-branch 命令进行历史重写,然后使用 git push --force 将更改推送到远程仓库。 步骤 1: 使用 git filter-branch 进行历史重写 在终端或命令行中执行以下命令: gi…...
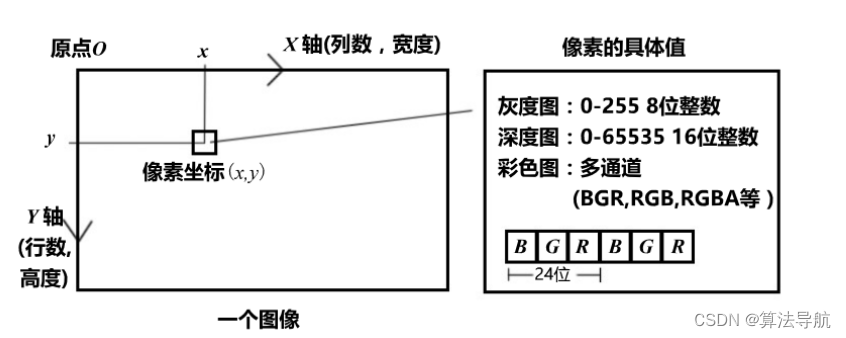
《视觉SLAM十四讲》-- 相机与图像
04 相机与图像 4.1 相机模型 4.1.1 针孔相机模型 针孔模型描述了一束光线通过针孔后,在针孔背面投影成像的关系(类似小孔成像原理)。 根据相似三角关系 Z f − X X ′ − Y Y ′ (3-1) \frac{Z}{f}-\frac{X}{X^{\prime}}-\frac{Y}{Y^{\p…...

欧科云链:成本与规模之辨——合规科技如何赋能香港Web3生态?
作为国际金融中心,香港近两年来在虚拟资产及Web3领域频频发力。秉持着“稳步创新”的基本逻辑,香港在虚拟资产与Web3领域已建立一定优势,但近期各类风险事件的发生则让业界的关注焦点再次转向“安全”与“合规”。 在香港FinTech Week前夕&a…...

【文献分享】NASA JPL团队CoSTAR一大力作:直接激光雷达里程计:利用密集点云快速定位
论文题目:Direct LiDAR Odometry: Fast Localization With Dense Point Clouds 中文题目:直接激光雷达里程计:利用密集点云快速定位 作者:Kenny Chen, Brett T.Lopez, Ali-akbar Agha-mohammadi 论文链接:https://arxiv.org/pd…...
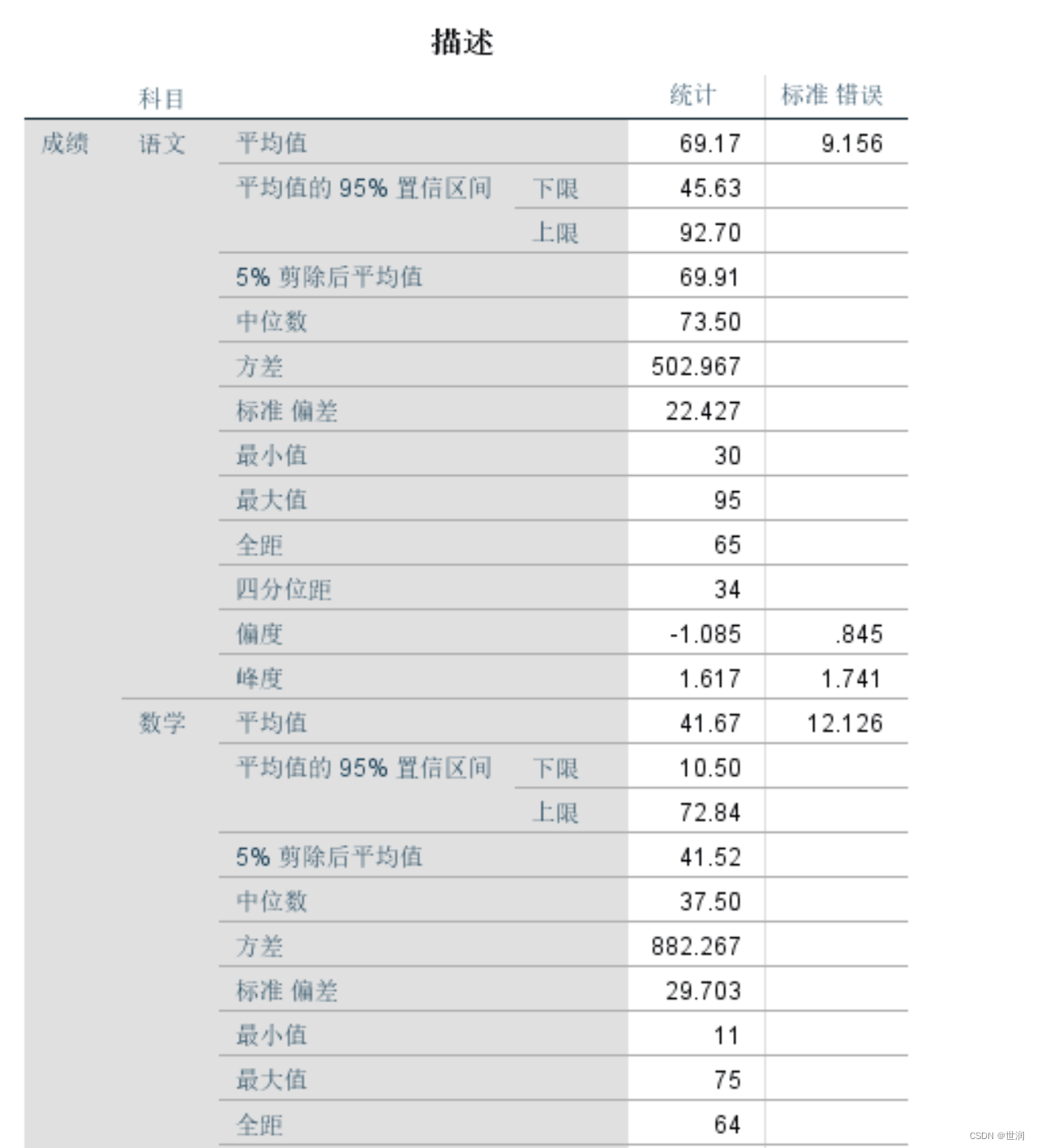
SPASS-探索性分析
探索性分析的意义 探索性分析更加强大,它是一种在对资料的性质、分布特点等完全不清楚的情况下,对变量进行更深入研究的描述性统计方法。在进行统计分析前,通常需要寻求和确定适合所研究的问题的统计方法, SPSS提供的探索性分析是解决此类问题的有效办法 探索性分析提供了很…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...

RLHF vs RLVR:对齐学习中的两种强化方式详解
在语言模型对齐(alignment)中,强化学习(RL)是一种重要的策略。而其中两种典型形式——RLHF(Reinforcement Learning with Human Feedback) 与 RLVR(Reinforcement Learning with Ver…...
