机器学习——回归
目录
一、线性回归
1、回归的概念(Regression、Prediction)
2、符号约定
3、算法流程
4、最小二乘法(LSM)
二、梯度下降
梯度下降的三种形式
1、批量梯度下降(Batch Gradient Descent,BGD):
2、随机梯度下降(Stochastic Gradient Descent,SGD):
3、小批量梯度下降(Mini-Batch Gradient Descent,MBGD):
梯度下降与最小二乘法比较
梯度下降:
最小二乘法:
数据归一化/标准化
为什么要标准化/归一化?
归一化(最大 - 最小规范化)
Z-Score标准化
需要做数据归一化/标准化
不需要做数据归一化/标准化
三、正则化
1、过拟合和欠拟合
2、过拟合的处理
3、 欠拟合的处理
4、正则化
四、回归的评价指标
一、线性回归
1、回归的概念(Regression、Prediction)
- 如何预测上海浦东的房价?
- 未来的股票市场走向?
线性回归(Linear Regression)是一种通过属性的线性组合来进行预测的线性模型,其目的是找到一条直线或者一个平面或者更高维的超平面,使得预测值与真实值之间的误差最小化。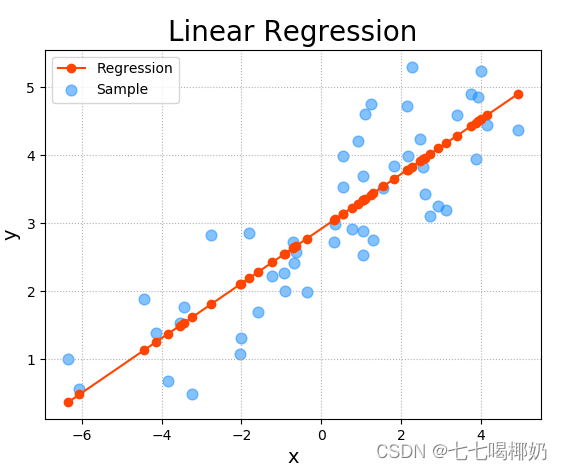
2、符号约定
- m 代表训练集中样本的数量
- n 代表特征的数量
- x 代表特征/输入变量
- y 代表目标变量/输出变量
- (x,y) 代表训练集中的样本
- (x^(i),y^(i)) 代表第i个观察样本
- ℎ 代表学习算法的解决方案或函数也称为假设(hypothesis)
- ̂┬y=ℎ(x),代表预测的值
建筑面积
总层数
楼层
实用面积
房价
143.7
31
10
105
36200
162.2
31
8
118
37000
199.5
10
10
170
42500
96.5
31
13
74
31200
……
……
……
……
……
x^(i)是特征矩阵中的第i行,是一个向量。
x_j^(i)代表特征矩阵中第 i 行的第 j 个特征
3、算法流程
损失函数(Loss Function):
度量单样本预测的错误程度,损失函数值越小,模型就越好。常用的损失函数包括:0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等。
代价函数(Cost Function):
度量全部样本集的平均误差。常用的代价函数包括均方误差、均方根误差、平均绝对误差等。
目标函数(Objective Function):
代价函数加正则化项,最终要优化的函数。
x 和 y 的关系: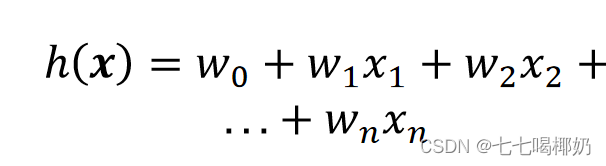
可以设x_0=1,则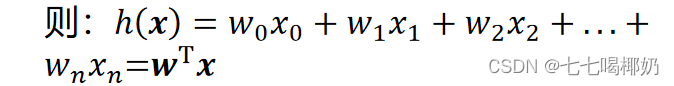
损失函数采用平方和损失: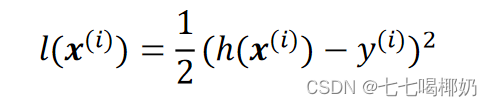
要找到一组 w(w_0,w_1,w_2,...,w_n) ,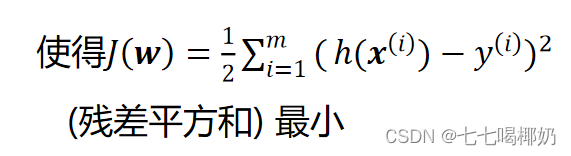
4、最小二乘法(LSM)
要找到一组 w(w_0,w_1,w_2,...,w_n) ,使得残差平方和最小。转为矩阵表达形式,令
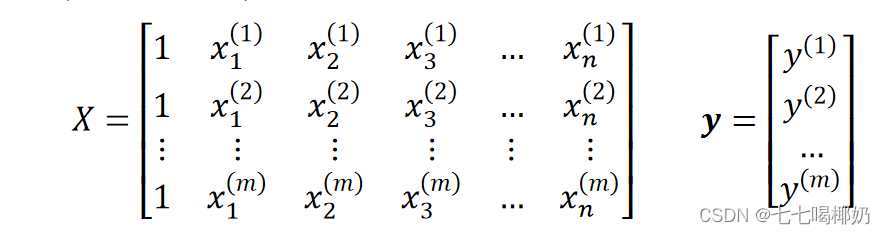
其中X为m行n+1列的矩阵(m为样本个数,n为特征个数),w为n+1行1列的矩阵(包含了w_0),Y为m行1列的矩阵,则 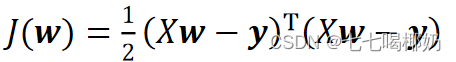
注:
(可由数学推导)
为最小化,接下来对J(w)偏导,
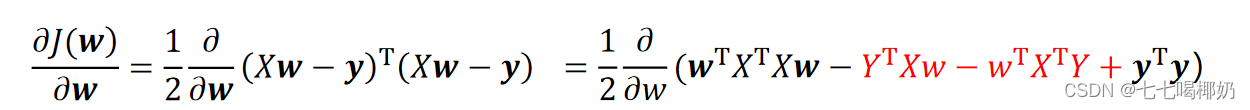
由于中间两项互为转置: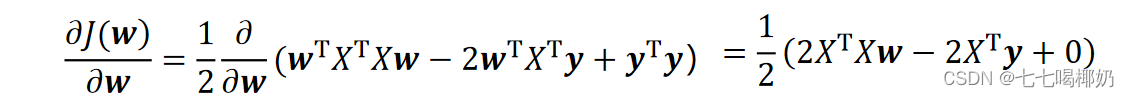
![]()
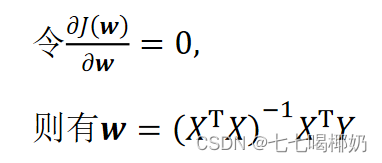
需要用到以下几个矩阵的求导结论:
二、梯度下降
梯度下降的三种形式
1、批量梯度下降(Batch Gradient Descent,BGD):
梯度下降的每一步中,都用到了所有的训练样本

2、随机梯度下降(Stochastic Gradient Descent,SGD):
度下降的每一步中,用到一个样本,在每一次计算之后便更新参数 ,而不需要首先将所有的训练集求和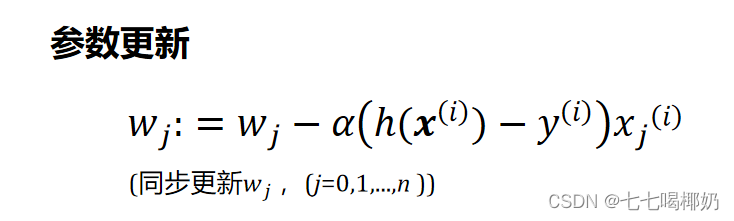
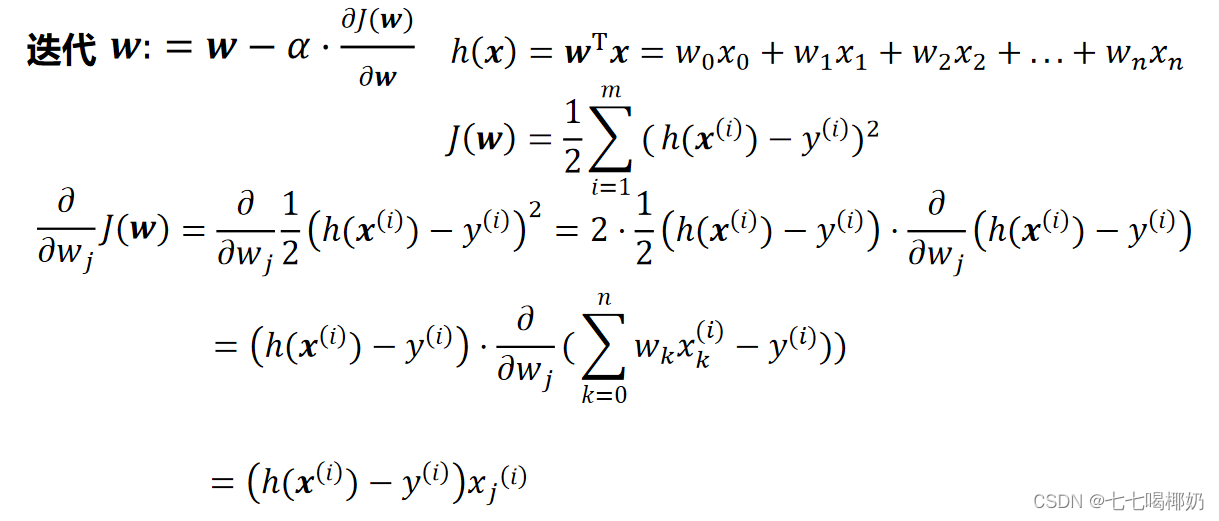
3、小批量梯度下降(Mini-Batch Gradient Descent,MBGD):
梯度下降的每一步中,用到了一定批量的训练样本
每计算常数b次训练实例,便更新一次参数 w
b=1(随机梯度下降,SGD)
b=m(批量梯度下降,BGD)
b=batch_size,通常是2的指数倍,常见有32,64,128等。(小批量梯度下降,MBGD)
梯度下降与最小二乘法比较
梯度下降:
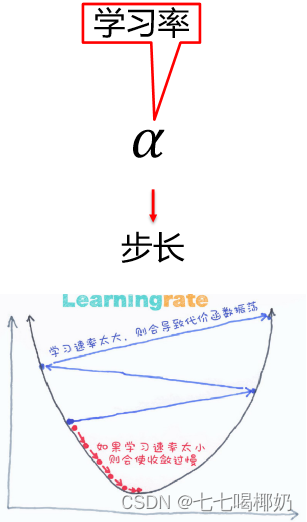
需要选择学习率α,需要多次迭代,当特征数量n大时也能较好适用,适用于各种类型的模型。
最小二乘法:
不需要选择学习率α,一次计算得出,需要计算(X^TX)^−1,如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为O(n^3),通常来说当n小于10000 时还是可以接受的,只适用于线性模型,不适合逻辑回归模型等其他模型。
数据归一化/标准化
为什么要标准化/归一化?
提升模型精度:不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性。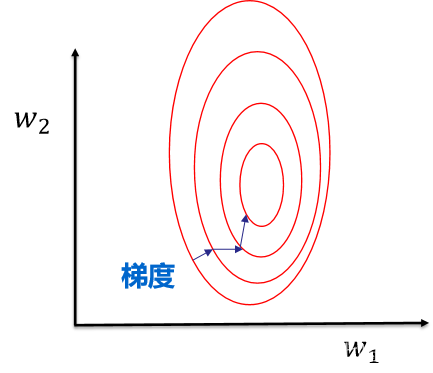
加速模型收敛:最优解的寻优过程明显会变得平缓,更容易正确的收敛到最优解。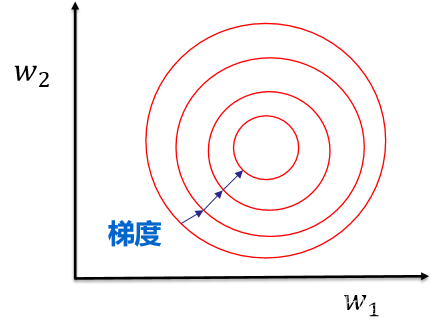
归一化(最大 - 最小规范化)
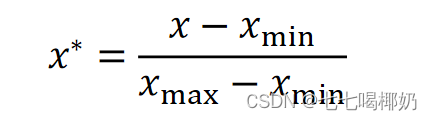
将数据映射到[0,1]区间
数据归一化的目的是使得各特征对目标变量的影响一致,会将特征数据进行伸缩变化,所以数据归一化是会改变特征数据分布的。
Z-Score标准化
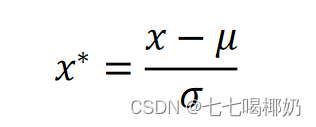

处理后的数据均值为0,方差为1
数据标准化为了不同特征之间具备可比性,经过标准化变换之后的特征数据分布没有发生改变。
就是当数据特征取值范围或单位差异较大时,最好是做一下标准化处理。
需要做数据归一化/标准化
线性模型,如基于距离度量的模型包括KNN(K近邻)、K-means聚类、感知机和SVM。另外,线性回归类的几个模型一般情况下也是需要做数据归一化/标准化处理的。
不需要做数据归一化/标准化
决策树、基于决策树的Boosting和Bagging等集成学习模型对于特征取值大小并不敏感,如随机森林、XGBoost、LightGBM等树模型,以及朴素贝叶斯,以上这些模型一般不需要做数据归一化/标准化处理。
三、正则化
1、过拟合和欠拟合
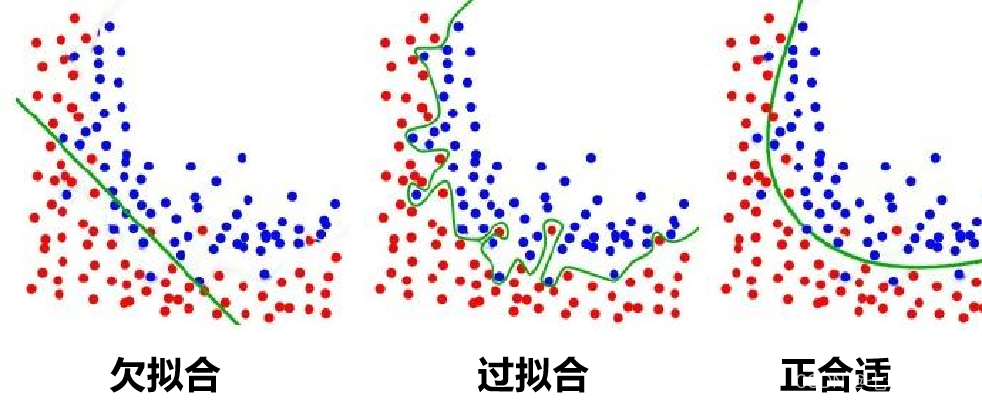
2、过拟合的处理
1.获得更多的训练数据
使用更多的训练数据是解决过拟合问题最有效的手段,因为更多的样本能够让模型学习到更多更有效的特征,减小噪声的影响。
2.降维
即丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)。
3.正则化
正则化(regularization)的技术,保留所有的特征,但是减少参数的大小(magnitude),它可以改善或者减少过拟合问题。
4.集成学习方法
集成学习是把多个模型集成在一起,来降低单一模型的过拟合风险。
3、 欠拟合的处理
1.添加新特征
当特征不足或者现有特征与样本标签的相关性不强时,模型容易出现欠拟合。通过挖掘组合特征等新的特征,往往能够取得更好的效果。
2.增加模型复杂度
简单模型的学习能力较差,通过增加模型的复杂度可以使模型拥有更强的拟合能力。例如,在线性模型中添加高次项,在神经网络模型中增加网络层数或神经元个数等。
3.减小正则化系数
正则化是用来防止过拟合的,但当模型出现欠拟合现象时,则需要有针对性地减小正则化系数。
4、正则化
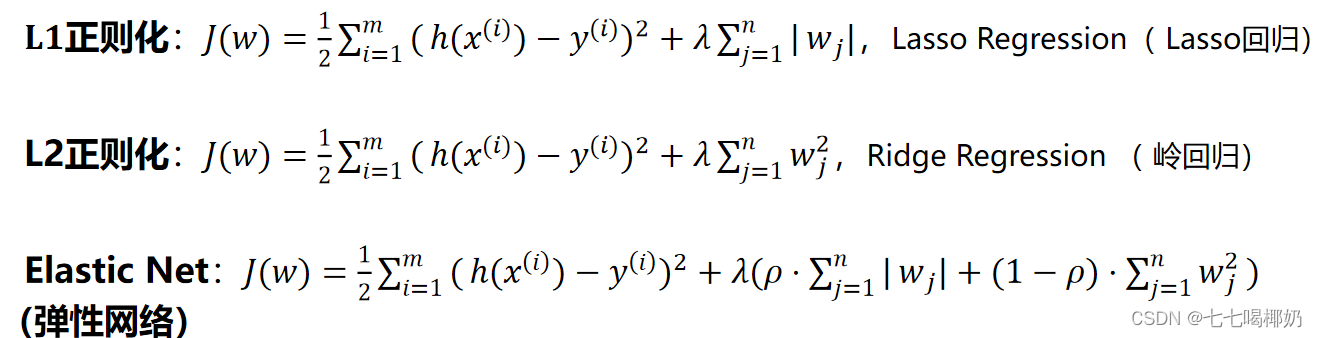
其中:
- λ为正则化系数,调整正则化项与训练误差的比例,λ>0。
- 1≥ρ≥0为比例系数,调整L1正则化与L2正则化的比例。
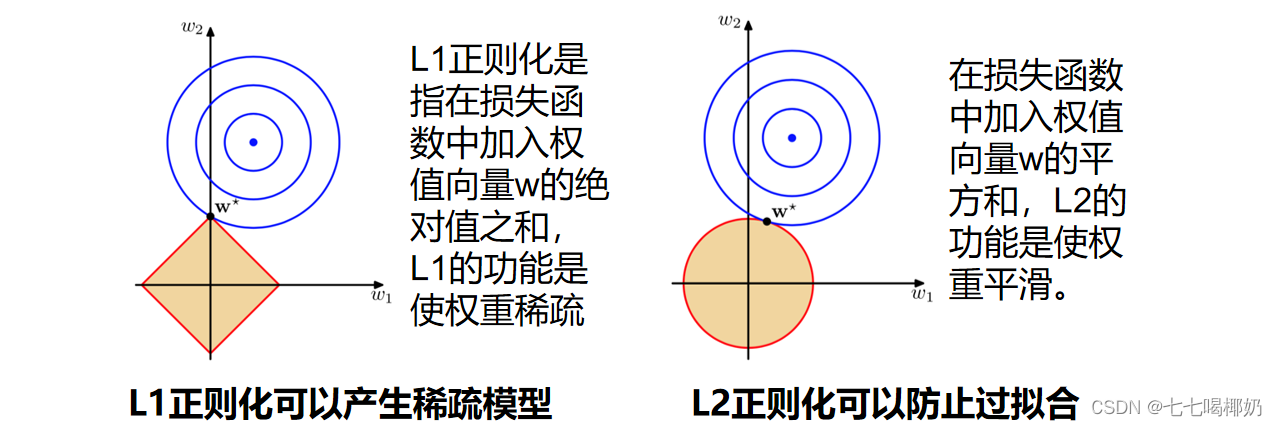
图上面中的蓝色轮廓线是没有正则化损失函数的等高线,中心的蓝色点为最优解,左图、右图分别为L1、L2正则化给出的限制。
可以看到在正则化的限制之下, L1正则化给出的最优解w*是使解更加靠近原点,也就是说L2正则化能降低参数范数的总和。
L1正则化给出的最优解w*是使解更加靠近某些轴,而其它的轴则为0,所以L1正则化能使得到的参数稀疏化。
四、回归的评价指标
均方误差(Mean Square Error,MSE)
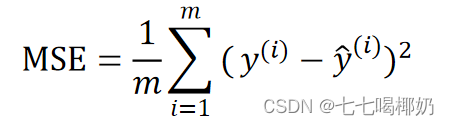
均方根误差 RMSE(Root Mean Square Error,RMSE)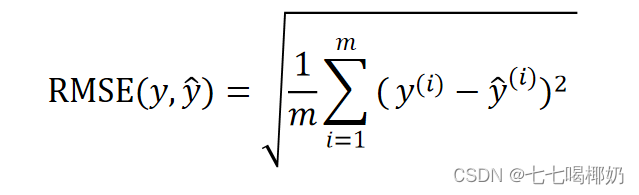
平均绝对误差(Mean Absolute Error,MAE)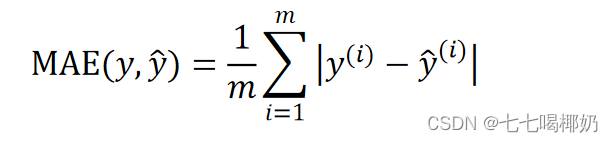

R方 [RSquared(r2score)] 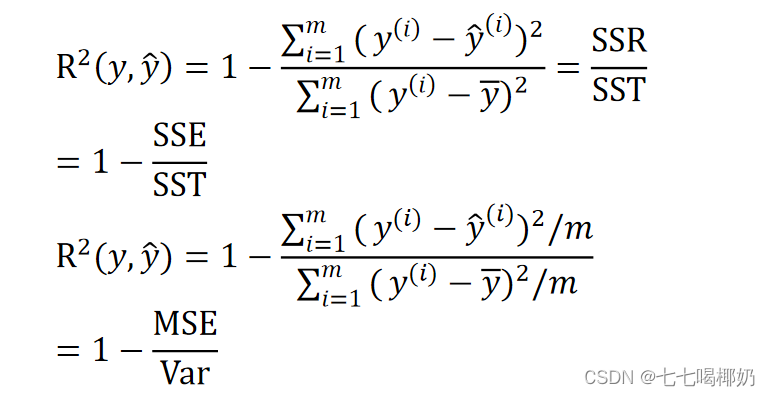
越接近于1,说明模型拟合得越好
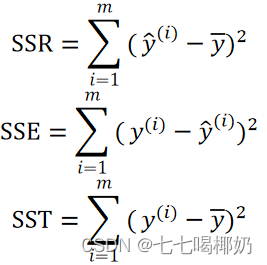
相关文章:
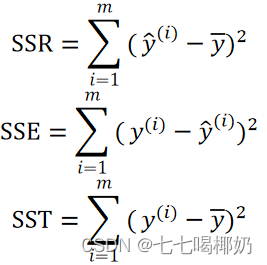
机器学习——回归
目录 一、线性回归 1、回归的概念(Regression、Prediction) 2、符号约定 3、算法流程 4、最小二乘法(LSM) 二、梯度下降 梯度下降的三种形式 1、批量梯度下降(Batch Gradient Descent,BGD)ÿ…...
JAVA代码视频转GIF(亲测有效)
1.说明 本次使用的是JAVA代码视频转GIF,maven如下: <dependency><groupId>ws.schild</groupId><artifactId>jave-nativebin-win64</artifactId><version>3.2.0</version></dependency><dependency&…...
挑战100天 AI In LeetCode Day03(热题+面试经典150题)
挑战100天 AI In LeetCode Day03(热题面试经典150题) 一、LeetCode介绍二、LeetCode 热题 HOT 100-52.1 题目2.2 题解 三、面试经典 150 题-53.1 题目3.2 题解 一、LeetCode介绍 LeetCode是一个在线编程网站,提供各种算法和数据结构的题目&am…...
【手写模拟Spring底层原理】
文章目录 模拟Spring底层详解1、结合配置类,扫描类资源1.1、创建需要扫描的配置类AppConfig,如下:1.2、创建Spring容器对象LyfApplicationContext,如下1.3、Spring容器对象LyfApplicationContext扫描资源 2、结合上一步的扫描&…...

代码随想录训练营Day1:二分查找与移除元素
本专栏内容为:代码随想录训练营学习专栏,用于记录训练营的学习经验分享与总结。 文档讲解:代码随想录 视频讲解:二分查找与移除元素 💓博主csdn个人主页:小小unicorn ⏩专栏分类:C 🚚…...
回归预测 | Matlab实现PCA-PLS主成分降维结合偏最小二乘回归预测
回归预测 | Matlab实现PCA-PLS主成分降维结合偏最小二乘回归预测 目录 回归预测 | Matlab实现PCA-PLS主成分降维结合偏最小二乘回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 Matlab实现PCA-PLS主成分降维结合偏小二乘回归预测(完整源码和数据) 1.输…...

高效的测试覆盖率:在更短的时间内最大化提高测试覆盖率
软件测试在敏捷开发生命周期中至关重要,而测试覆盖率又是软件测试的一个重要指标,有效的测试覆盖率对软件测试来说永远是重中之重。测试覆盖率确保所有关键功能和特性都经过彻底测试,减少最终产品中出现错误和错误的可能性(取决于…...
Qt 项目实战 | 音乐播放器
Qt 项目实战 | 音乐播放器 Qt 项目实战 | 音乐播放器播放器整体架构创建播放器主界面媒体对象状态实现播放列表实现桌面歌词添加系统托盘图标 资源下载 官方博客:https://www.yafeilinux.com/ Qt开源社区:https://www.qter.org/ 参考书:《Q…...

JavaScript使用Ajax
Ajax(Asynchronous JavaScript and XML)是使用JavaScript脚本,借助XMLHttpRequest插件,在客户端与服务器端之间实现异步通信的一种方法。2005年2月,Ajax第一次正式出现,从此以后Ajax成为JavaScript发起HTTP异步请求的代名词。2006…...
Python爬虫实战-批量爬取美女图片网下载图片
大家好,我是python222小锋老师。 近日锋哥又卷了一波Python实战课程-批量爬取美女图片网下载图片,主要是巩固下Python爬虫基础 视频版教程: Python爬虫实战-批量爬取美女图片网下载图片 视频教程_哔哩哔哩_bilibiliPython爬虫实战-批量爬取…...
uniapp+uview2.0+vuex实现自定义tabbar组件
效果图 1.在components文件夹中新建MyTabbar组件 2.组件代码 <template><view class"myTabbarBox" :style"{ backgroundColor: backgroundColor }"><u-tabbar :placeholder"true" zIndex"0" :value"MyTabbarS…...

opencv 任意两点切割图像
目录 opencv python直线切割图像,把图像分为两个多边形 升级版,把多边形分割抠图出来,取最小外接矩形:...
rust变量绑定、拷贝、转移、引用
目录 一,clone、copy 1,基本类型 2,类型的clone特征 3,显式声明结构体的clone特征 4,类型的copy特征 5,显式声明结构体的clone特征 5,变量和字面量的特征 6,特征总结 二&am…...

Java多种方式向图片添加自定义水印、图片转换及webp图片压缩
给个创建水印的示例: /*** 获取水印** param watermarkText 水印文字* return 水印bufferimage*/public static BufferedImage getWatermark(String watermarkText) {BufferedImage measureBufferdImage new BufferedImage(100, 100, BufferedImage.TYPE_INT_ARGB…...
——多维度单步预测)
基于Pytorch框架的LSTM算法(二)——多维度单步预测
1.项目说明 **选用Close和Low两个特征,使用窗口time_steps窗口的2个特征,然后预测Close这一个特征数据未来一天的数据 当batch_firstTrue,则LSTM的inputs(batch_size,time_steps,input_size) batch_size len(data)-time_steps time_steps 滑动窗口&…...

cnn感受野计算方法
No. Layers Kernel Size Stride 1 Conv1 33 1 2 Pool1 22 2 3 Conv2 33 1 4 Pool2 22 2 5 Conv3 33 1 6 Conv4 33 1 7 Pool3 2*2 2 感受野初始值 l 0 1 l_0 1l 0 1,每层的感受野计算过程如下: l 0 1 l_0 1l 0 1 l 1 1 ( 3 − 1 ) 3 l_1 1…...

百分点科技受邀参加“第五届治理现代化论坛”
11月4日,由北京大学政府管理学院主办的“面向新时代的人才培养——第五届治理现代化论坛”举行,北京大学校党委常委、副校长、教务长王博,政府管理学院院长燕继荣参加开幕式并致辞,百分点科技董事长兼CEO苏萌受邀出席论坛…...

基于Springboot的智慧食堂设计与实现(有报告)。Javaee项目,springboot项目。
演示视频: 基于Springboot的智慧食堂设计与实现(有报告)。Javaee项目,springboot项目。 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 项…...

「Verilog学习笔记」多功能数据处理器
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 分析 注意题目要求输入信号为有符号数,另外输出信号可能是输入信号的和,所以需要拓展一位,防止溢出。 timescale 1ns/1ns module data_…...

OpenHarmony 4.0 Release 编译异常处理
一、环境配置 编译环境:Ubuntu 20.04 OpenHarmony 软件版本:4.0 Release 设备平台:rk3568 二、下拉代码 参考官网步骤: OpenHarmony 4.0 Release 源码获取 repo init -u https://gitee.com/openharmony/manifest -b OpenHarmo…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

