2023NOIP A层联测28-大眼鸹猫
给你两个长度为 n n n 的序列 a , b a,b a,b,这两个序列都是单调不降的。
你可以对 a a a 进行不超过 m m m 次操作,每次操作你可以选择一个 i i i 满足 1 ≤ i ≤ n 1\le i\le n 1≤i≤n,然后选择一个整数(可以是负数) x x x,将 a i a_i ai 加上 x x x,这一次操作需要花费 x 2 x^2 x2 的代价。
在做操作的过程中,你需要保证 a a a 始终单调不降。
最后,你需要将 a a a 序列变成 b b b 序列,即对任意 i i i 满足 1 ≤ i ≤ n 1\le i\le n 1≤i≤n,都有 a i = b i a_i=b_i ai=bi。
求最小需要花费的总代价之和。
n , m ≤ 1 0 5 n,m\le10^5 n,m≤105
首先如果 m m m 小于 a i ≠ b i a_i\not=b_i ai=bi 的个数,就是无解了。
操作过程中,要保证 a a a 始终单调不降,看上去很难满足,但结论是一定存在一种合法操作方案。可以考虑一个极大的区间 [ l , r ] [l,r] [l,r], ∀ i ∈ [ l , r ] , a i < b i \forall i\in[l,r],a_i< b_i ∀i∈[l,r],ai<bi,此时就从 r r r 操作到 l l l,若 ∀ i ∈ [ l , r ] , a i > b i \forall i\in[l,r],a_i>b_i ∀i∈[l,r],ai>bi,就从 l l l 操作到 r r r。
所以单独考虑每一个数 ∣ a i − b i ∣ |a_i-b_i| ∣ai−bi∣,分配了 x i x_i xi 次操作,显然每次操作将 ∣ a i − b i ∣ |a_i-b_i| ∣ai−bi∣ 减少 ∣ a i − b i ∣ x i \dfrac{|a_i-b_i|}{x_i} xi∣ai−bi∣ 是代价最小的。设 f ( x ) f(x) f(x) 表示给 ∣ a i − b i ∣ |a_i-b_i| ∣ai−bi∣ 分配了 x x x 次操作的最小代价,发现 f ( x ) f(x) f(x) 是下凸函数,意思是随着 x x x 的增大, f ( x ) f(x) f(x) 减小的幅度越来越小。
那么我们可以先给每个数分配一次操作,对于剩下的操作用大根堆维护每个数再分配一次操作减少的代价,每次就贪心的去选代价减少得最多的,然后给它分配一次操作再放进堆里。最后把堆里的数拿出来算答案即可。
时间复杂度 O ( m log n ) O(m\log n) O(mlogn)。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
constexpr int N=1e5+1;
constexpr ll mod=998244353;
int n,m;
ll a[N],b[N],dis[N],ans;
inline ll getval(ll x,ll n)
{return (x/n)*(x/n)*(n-x%n)+(x/n+1)*(x/n+1)*(x%n);
}
struct node
{int num,id;bool operator<(const node &a)const{return getval(dis[id],num)-getval(dis[id],num+1)<getval(dis[a.id],a.num)-getval(dis[a.id],a.num+1);}
};
priority_queue<node> q;
int main()
{freopen("attend.in","r",stdin);freopen("attend.out","w",stdout);cin.tie(0)->sync_with_stdio(0);cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) cin>>b[i];int fl=0;for(int i=1;i<=n;i++) fl+=(a[i]!=b[i]);if(fl>m) cout<<"-1",exit(0);for(int i=1;i<=n;i++){if(a[i]==b[i]) continue;dis[i]=abs(a[i]-b[i]);q.push({1,i});}if(q.empty()) cout<<0,exit(0);m-=fl;while(m--){node now=q.top();q.pop();now.num++;q.push(now);}while(q.size()){ans=(ans+getval(dis[q.top().id],q.top().num))%mod;q.pop();}cout<<ans;
}
相关文章:

2023NOIP A层联测28-大眼鸹猫
给你两个长度为 n n n 的序列 a , b a,b a,b,这两个序列都是单调不降的。 你可以对 a a a 进行不超过 m m m 次操作,每次操作你可以选择一个 i i i 满足 1 ≤ i ≤ n 1\le i\le n 1≤i≤n,然后选择一个整数(可以是负数&…...
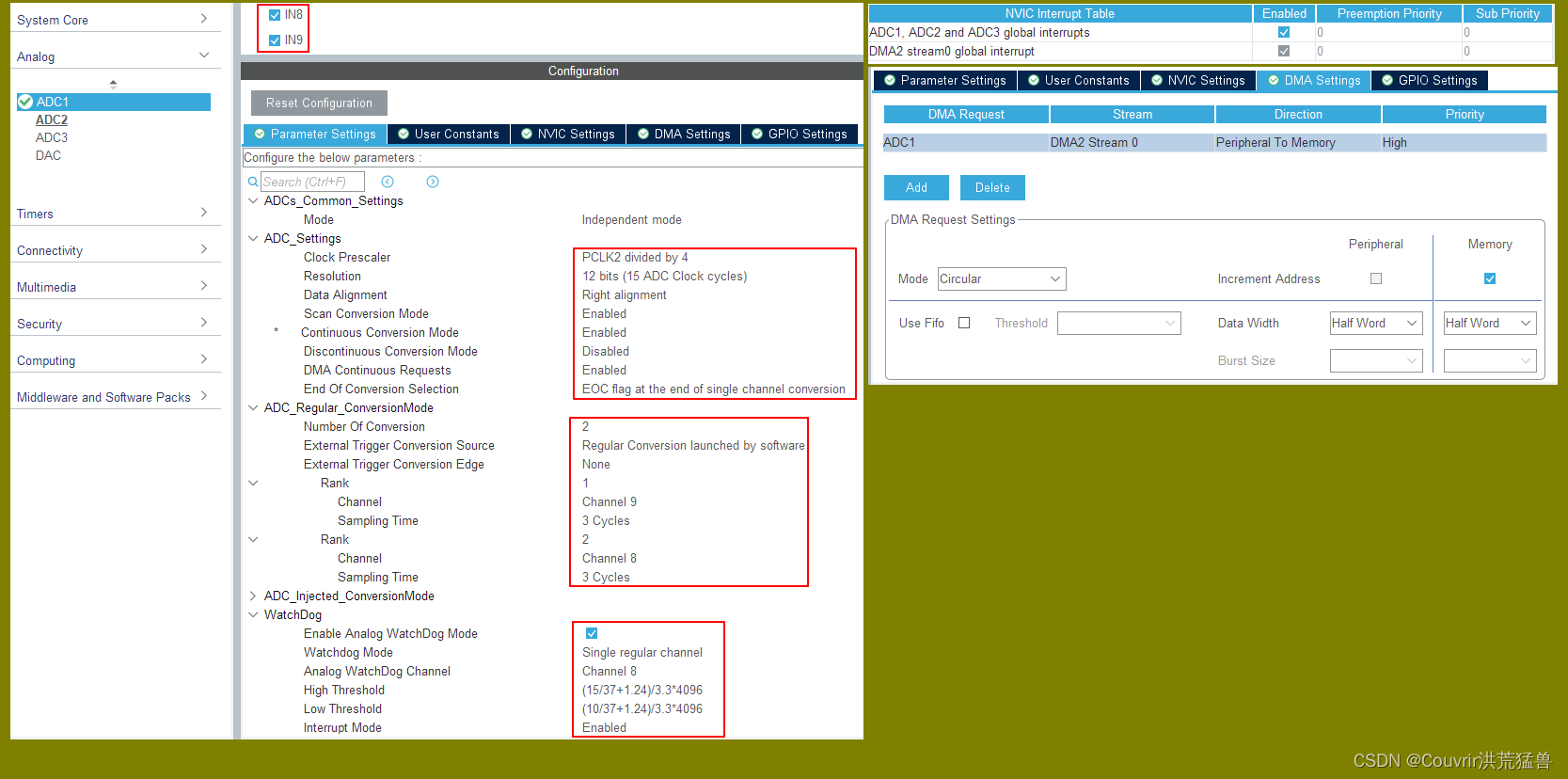
电机应用-直流有刷电机
目录 直流有刷电机 工作原理 直流有刷减速电机的重要参数 电路原理与分析 驱动芯片分析 L298N驱动芯片 直流有刷减速电机控制实现 控制速度原理 硬件设计 L298N 野火直流有刷电机驱动板-MOS管搭建板 软件设计1:两个直流有刷减速电机按键控制 开发设计 …...

BIM、建筑机器人、隧道工程施工关键技术
一、BIM简介 (一)BIM概念 BIM(Building Information Modeling),建筑信息模型。该技术通过数字化手段,在计算机中建立虚拟建筑,该虚拟建筑提供从单一到完整、包含逻辑关系的建筑信息库。信息库…...
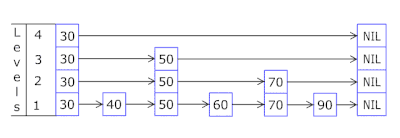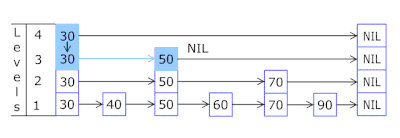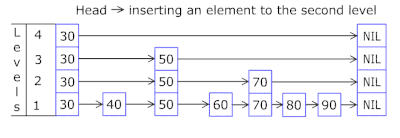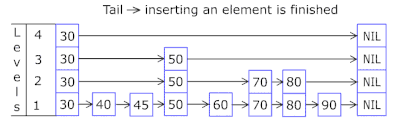
快速了解什么是跳跃表(skip list)
什么是跳跃表(skip list) 跳跃表(Skip List)是一种概率性的数据结构,它通过在多层链表的基础上添加“快速通道”来提高搜索效率。跳跃表的效率可以与平衡树相媲美,即在平均和最坏的情况下,查找…...

【Node.js入门】1.1Node.js 简介
Node.js入门之—1.1Node.js 简介 文章目录 Node.js入门之—1.1Node.js 简介什么是 Node.js错误说法 Node.js 的特点跨平台三方类库自带http服务器非阻塞I/O事件驱动单线程 Node.js 的应用场合适合用Node.js的场合不适合用Node.js的场合弥补Node.js不足的解决方案 什么是 Node.j…...
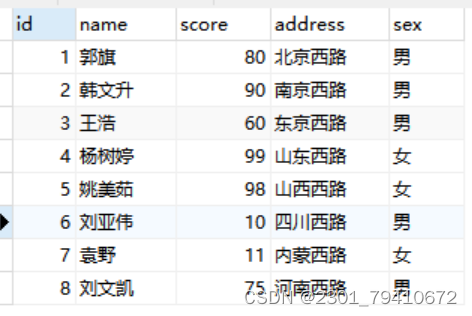
数据库 高阶语句
目录 数据库 高阶语句 使用select 语句,用order by来对进行排序 区间判断查询和去重查询 如何对结果进行分组查询group by语句 limit 限制输出的结果记录,查看表中的指定行 通配符 设置别名:alias 简写就是 as 使用select 语句&#x…...
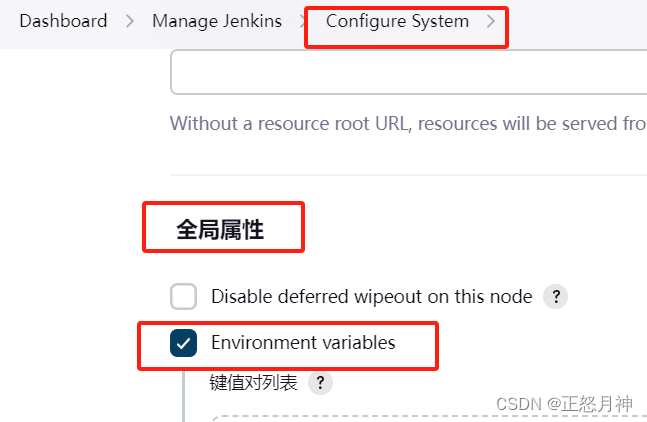
jenkins Java heap space
jenkins Java heap space,是内存不够。 两个解决方案: 一,修改配置文件 windows系统中,找到Jenkins的安装路径, 修改jenkins.xml 将 -Xmx256m 改为 -Xmx1024m 或者更大 重启jenkins服务。 二,jenkins增…...

OpenCV校准棋盘集合
棋盘格可以与相机校准工具一起使用,例如ROS的camera_calibration包。您可以通过单击下面的任何链接免费下载 PDF 格式的各种棋盘,没有水印或广告。此外,还添加了基于 JavaScript 的棋盘生成器,允许您生成自定义尺寸。 提示&#…...

使用git将本地项目推送到远程仓库github
总结:本地项目通过git上传到github 1)、在本地创建一个版本库(即文件夹),通过 git init 把它变成Git仓库; 2)、把项目复制到这个文件夹里面,再通过 git add . 把项目添加到仓库; 3)、再通过 gi…...
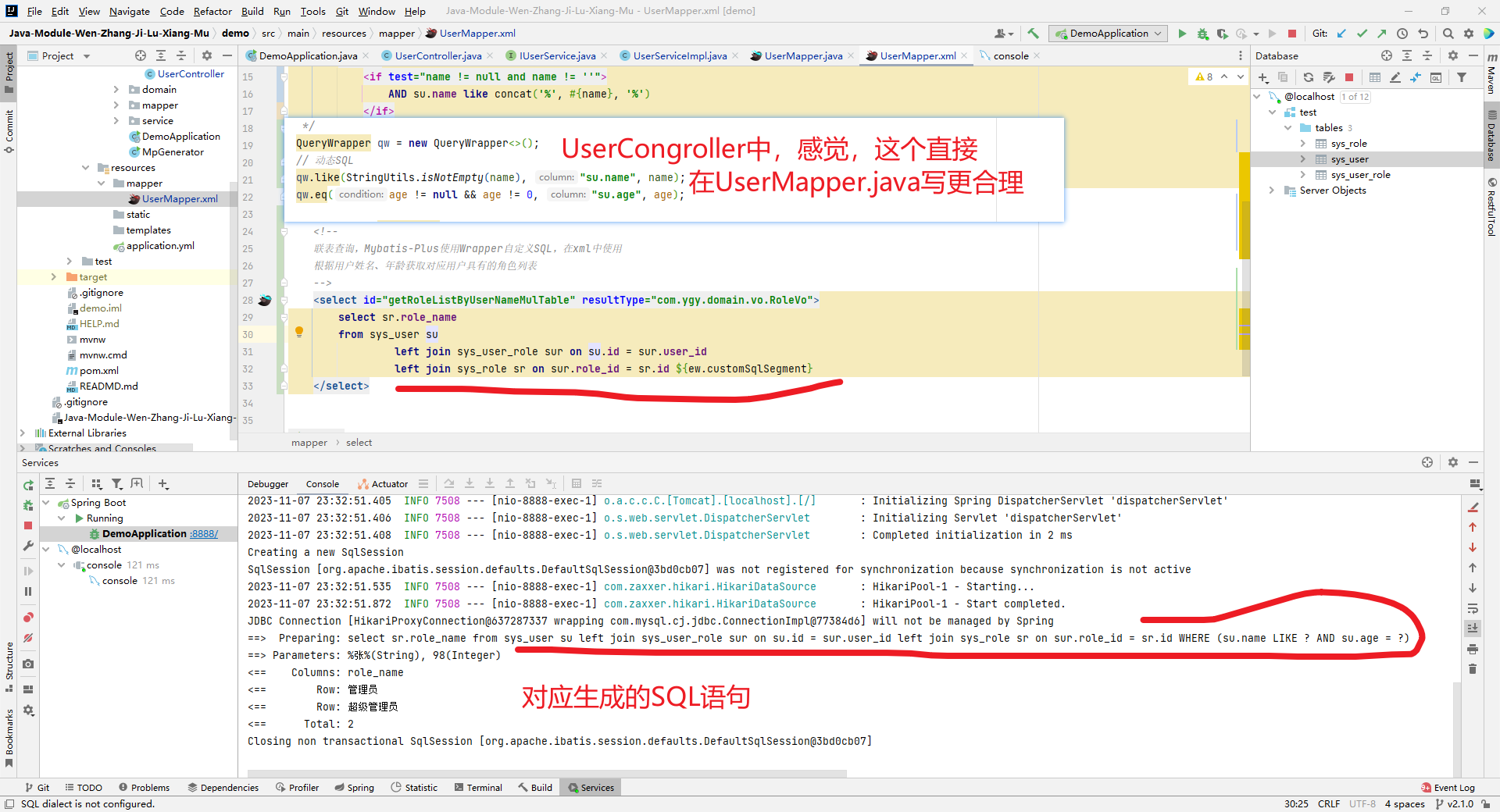
Mybatis-Plus使用Wrapper自定义SQL
文章目录 准备工作Mybatis-Plus使用Wrapper自定义SQL注意事项目录结构如下所示domain层Controller层Service层ServiceImplMapper层UserMapper.xml 结果如下所示:单表查询条件构造器单表查询,Mybatis-Plus使用Wrapper自定义SQL联表查询不用,My…...
仿mudou库one thread one loop式并发服务器
目录 1.实现目标 2.HTTP服务器 实现高性能服务器-Reactor模型 模块划分 SERVER模块: HTTP协议模块: 3.项目中的子功能 秒级定时任务实现 时间轮实现 正则库的简单使用 通⽤类型any类型的实现 4.SERVER服务器实现 日志宏的封装 缓冲区Buffer…...

二十三种设计模式全面解析-组合模式与装饰器模式的结合:实现动态功能扩展
在前文中,我们介绍了组合模式的基本原理和应用,以及它在构建对象结构中的价值和潜力。然而,组合模式的魅力远不止于此。在本文中,我们将继续探索组合模式的进阶应用,并展示它与其他设计模式的结合使用,以构…...
智慧城市建设解决方案分享【完整】
文章目录 第1章 前言第2章 智慧城市建设的背景2.1 智慧城市的发展现状2.2 智慧城市的发展趋势 第3章 智慧城市“十二五”规划要点3.1 国民经济和社会发展“十二五”规划要点3.2 “十二五”信息化发展规划要点 第4章 大数据:智慧城市的智慧引擎4.1 大数据技术—智慧城…...

unity - Blend Shape - 变形器 - 实践
文章目录 目的Blend Shape 逐顶点 多个混合思路Blender3Ds maxUnity 中使用Project 目的 拾遗,备份 Blend Shape 逐顶点 多个混合思路 blend shape 基于: vertex number, vertex sn 相同,才能正常混合、播放 也就是 vertex buffer 的顶点数…...
asp.net core mvc之路由
一、默认路由 (Startup.cs文件) routes.MapRoute(name: "default",template: "{controllerHome}/{actionIndex}/{id?}" ); 默认访问可以匹配到 https://localhost:44302/home/index/1 https://localhost:44302/home/index https:…...

前端设计模式之【访问者模式】
文章目录 前言介绍实现优缺点应用场景后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:前端设计模式 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。(如果出现错误&#…...
通过docker-compose部署elk日志系统,并使用springboot整合
ELK是一种强大的分布式日志管理解决方案,它由三个核心组件组成: Elasticsearch:作为分布式搜索和分析引擎,Elasticsearch能够快速地存储、搜索和分析大量的日志数据,帮助用户轻松地找到所需的信息。 Logstash…...

【NLP】特征提取: 广泛指南和 3 个操作教程 [Python、CNN、BERT]
什么是机器学习中的特征提取? 特征提取是数据分析和机器学习中的基本概念,是将原始数据转换为更适合分析或建模的格式过程中的关键步骤。特征,也称为变量或属性,是我们用来进行预测、对对象进行分类或从数据中获取见解的数据点的…...
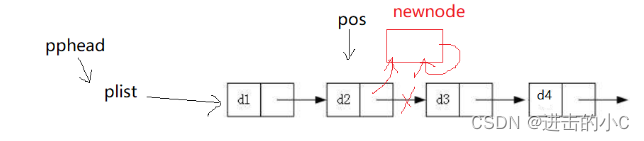
数据结构-单链表
1 链表的概念及结构 概念:链表是一种物理存储结构上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的 。 从以上图片可以看出: 1.链式结构在逻辑上是连续的,但在物理上不一定是连续的。 2.现实中的节…...
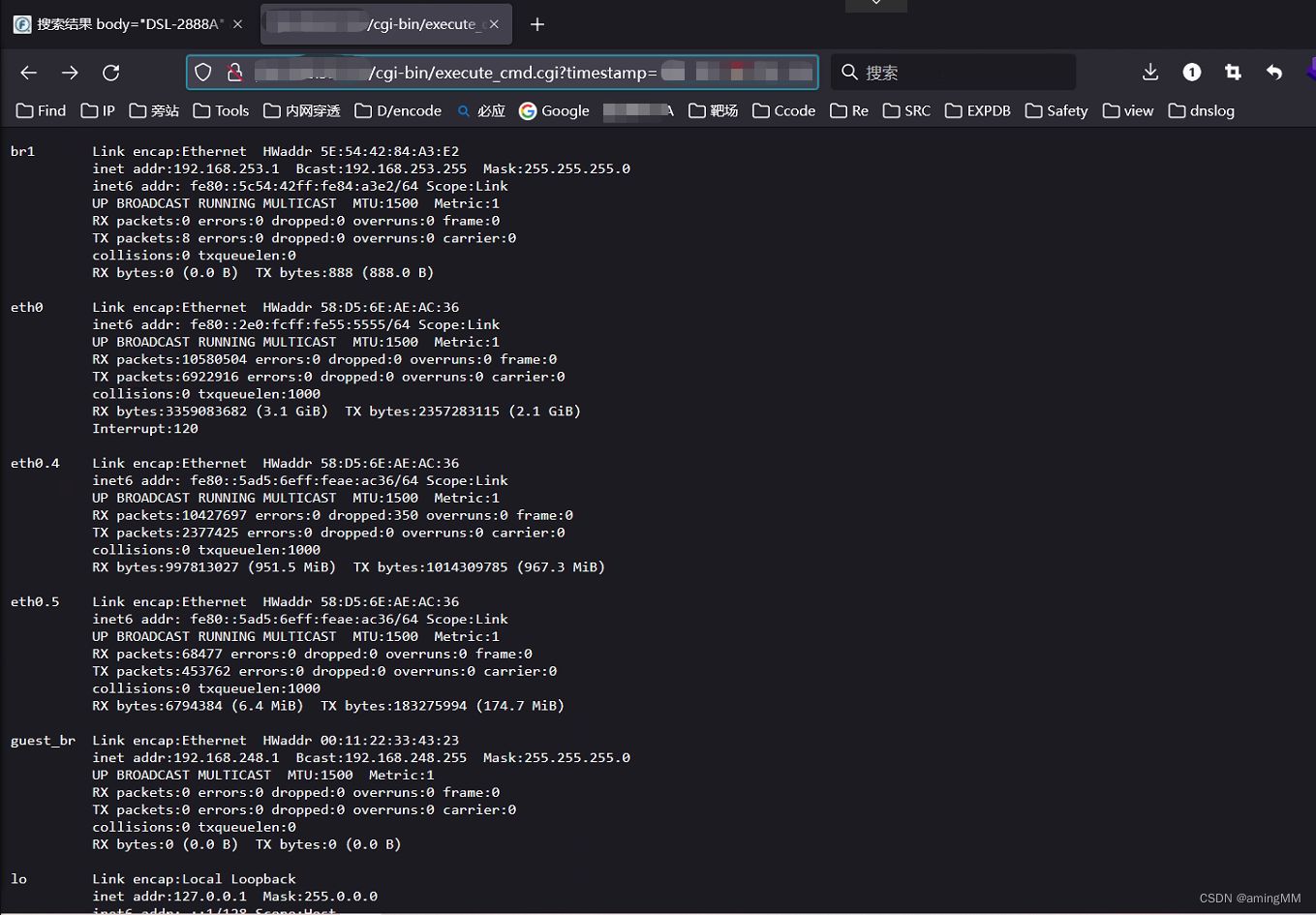
红队系列-IOT安全深入浅出
红队专题 设备安全概述物联网设备层次模型设备通信模型 渗透测试信息收集工具 实战分析漏洞切入点D-link 850L 未授权访问 2017 认证绕过认证绕过 D-link DCS-2530Ltenda 系列 路由器 前台未授权RTSP 服务未授权 访问 弱口令命令注入思科 路由器 固件二进制 漏洞 IoT漏洞-D-Lin…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
