当前位置： 首页 > news >正文

查找或替换excel换行符ctrl+j和word中的换行符^p,^l

news 2026/2/9 21:20:56

一、excel中

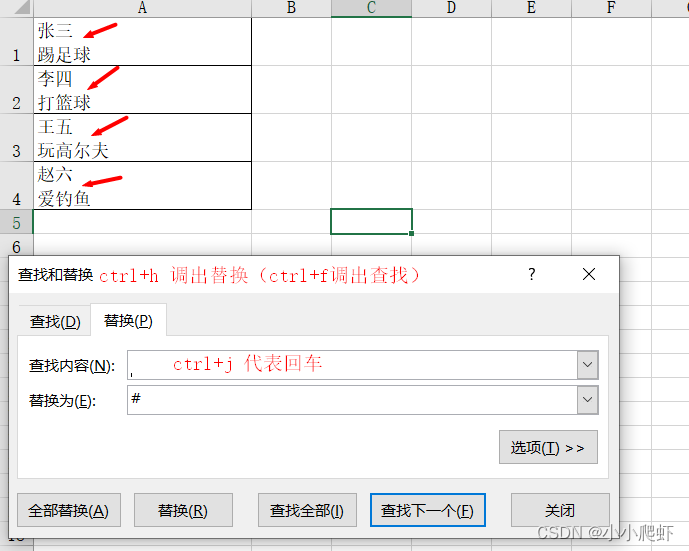
直接上图。使用ctrl+h调出替换，查找内容里按ctrl+j（会出现一个闪的小点），即为换行符。

二、word中

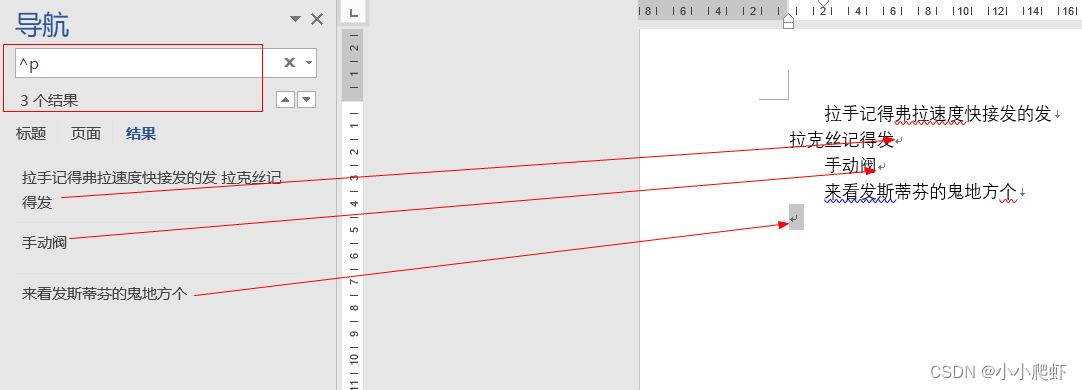
在word中，^p和^l分别代表换行符（enter）和手动换行符（使用shift+enter）。

^l是手动换行符，符号是一个向下的小箭头。^p是回车，符号是一个拐弯的小箭头。

他们两个的区别是：

1、^l只是换行，但没有分段，就是说，^l前后的文字同属于一段，首行缩进等格式对^l下一行的文字是无效的。

2、^p是回车符，他的作用是，换行、分段。^p之后的文字形成一个新的段落。

3、换行符一般在需要项目符号和编号的时候用到。

查找或者替换的方法，ctrl+h或者f，

相关文章：

查找或替换excel换行符ctrl+j和word中的换行符^p,^l

一、excel中 直接上图。使用ctrlh调出替换，查找内容里按ctrlj（会出现一个闪的小点），即为换行符。 二、word中 在word中，^p和^l分别代表换行符（enter）和手动换行符（使用shiftenter&…...

编程日记 2023/11/10 23:01:51

pytorch_神经网络构建5

文章目录 生成对抗网络自动编码器变分自动编码器重参数GANS自动编码器变分自动编码器gans网络Least Squares GANDeep Convolutional GANs 生成对抗网络 这起源于一种思想,假如有一个生成器,从原始图片那里学习东西,一个判别器来判别图片是真实的还是生成的, 假如生成的东西能以…...

编程日记 2023/11/10 23:00:51

安卓常见设计模式5------桥接模式（Kotlin版）

1. W1 是什么，什么是桥接模式？ 桥接模式是一种结构性模式。 桥接模式旨在将抽象与实现解耦，使它们可以独立地变化。可以这么理解，面向对象编程是单继承多实现的，如果我们有一个可扩展类，和多个相关的可扩展…...

编程日记 2023/11/10 22:59:49

tomcat web.xml文件中的session-config

<session-config>这个元素为该应用中创建的所有session定义默认超时时间&#xff0c;单位是分钟。这个值必须是整数。如果是0或者负数&#xff0c;表示不超时。如果该元素没有设置&#xff0c;容器设置一个默认值。 例如&#xff1a; <session-config><session…...

编程日记 2023/11/10 22:58:48

Hadoop知识点全面总结

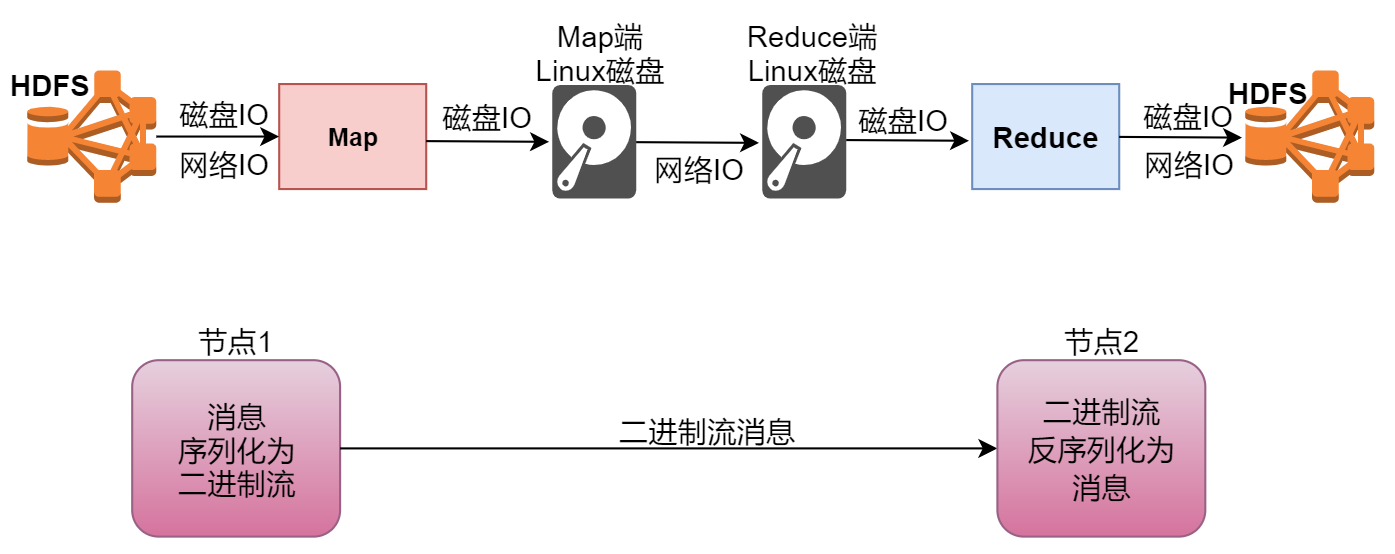
文章目录 什么是HadoopHadoop发行版介绍Hadoop版本演变历史Hadoop3.x的细节优化Hadoop三大核心组件介绍HDFS体系结构NameNode介绍总结 SecondaryNameNode介绍DataNode介绍DataNode总结 MapReduce介绍分布式计算介绍MapReduce原理剖析MapReduce之Map阶段MapReduce之Reduce阶段 实…...

编程日记 2023/11/10 22:57:47

MSVCP140_CODECVT_IDS.dll丢失怎么办？推荐三个解决方法帮你解决

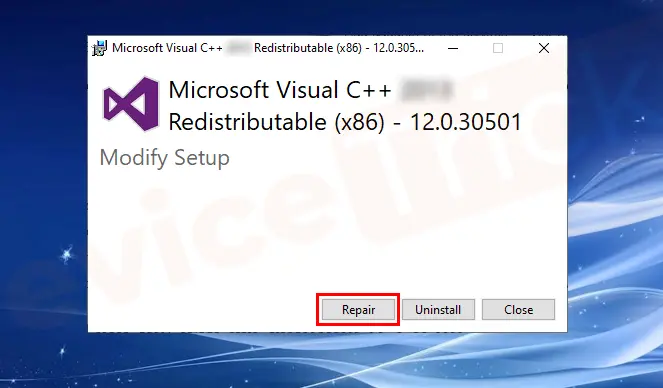
MSVCP140_CODECVT_IDS.dll是Microsoft Visual C 2015 Redistributable的一个组件&#xff0c;它包含了一些运行时库文件。当您在运行某些程序时&#xff0c;可能会遇到“msvcp140_codecvt_ids.dll丢失”的错误提示。为了解决这个问题&#xff0c;您可以尝试以下三种方法&#x…...

编程日记 2023/11/10 22:55:43

问题描述：64位计算机的寻址能力是多少TB

问题描述&#xff1a;64位计算机的寻址能力是多少TB 我在看到一个32位电脑的寻址能力计算时&#xff0c;看到是这么计算的。 虚拟内存的大小受到计算机地址位数的限制&#xff0c; 那么32位电脑的寻址能力计算应该是这样 为什么网上百度到的是16TB呢&#xff0c;如下图所示 中…...

编程日记 2023/11/10 22:54:42

【算法 | 数论 No.1】AcWing1246. 等差数列

个人主页&#xff1a;兜里有颗棉花糖 欢迎 点赞&#x1f44d; 收藏✨ 留言✉ 加关注&#x1f493;本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【AcWing算法提高学习专栏】 &#x1f354;本专栏旨在提高自己算法能力的同时&#xff0c;记录一下自己的学习过程&a…...

编程日记 2023/11/10 22:53:41

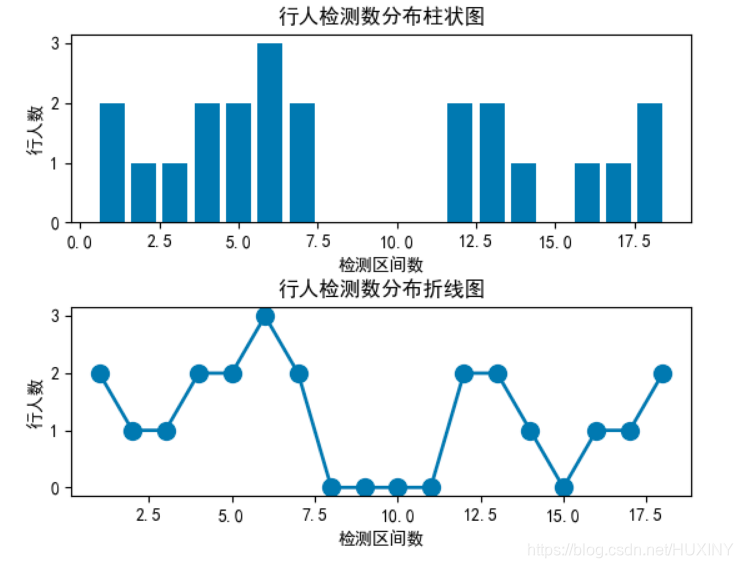
竞赛 目标检测-行人车辆检测流量计数

文章目录 前言1\. 目标检测概况1.1 什么是目标检测&#xff1f;1.2 发展阶段 2\. 行人检测2.1 行人检测简介2.2 行人检测技术难点2.3 行人检测实现效果2.4 关键代码-训练过程 最后 前言 &#x1f525; 优质竞赛项目系列&#xff0c;今天要分享的是 行人车辆目标检测计数系统 …...

编程日记 2023/11/10 22:52:40

秋招进入尾声了，还有哪些公司和岗位可以投递？

24届秋招基本已经进入尾声了&#xff0c;接下来就是秋招补录了&#xff0c;最近在微信群看到一些同学再问哪些公司还在招人的。 在这里跟大家分享一份2024届秋招信息汇总表&#xff0c;目前已更新2000家&#xff0c;不仅有互联网公司&#xff0c;还有外企、国企、各类研究所&am…...

编程日记 2023/11/10 22:51:39

CSS 文字溢出省略号显示

1. 单行文本溢出显示省略号 需要满足三个条件&#xff0c;添加对应的代码&#xff1a; &#xff08;1&#xff09;先强制一行内显示文本&#xff1b; &#xff08;2&#xff09;超出的部分隐藏&#xff1b; &#xff08;3&#xff09;文字用省略号来替代省略的部分&#xf…...

编程日记 2023/11/10 22:50:37

POD创建与删除简单描述

创建一个 Pod 的过程可以分为以下几个步骤&#xff1a; 用户使用 kubectl create 命令或 YAML 文件向 API 服务器发送创建 Pod 的请求。API 服务器将请求转换为 Kubernetes 的内部对象&#xff0c;并将 Pod 的状态设置为 Pending。调度器根据 Pod 的资源需求和节点的资源情况&…...

编程日记 2023/11/10 22:49:36

AndroidStudio打包报错记录(commons-logging，keystore password was incorrect)

场景&#xff1a; AndroidStudio2022打包APK的时报错 1.commons-logging依赖冲突 报错主要信息如下 Error: commons-logging defines classes that conflict with classes now provided by Android. 通过报错信息可以看出&#xff0c;项目中的commons-logging与Android系统自带…...

编程日记 2023/11/10 22:48:35

如何构建企业数据资产？数据资产如何入资产负债表 ?

一、构建企业数据资产 1. 数据收集 需要从多渠道收集数据&#xff0c;包括企业内部系统、市场调研、社交媒体、客户反馈等。在收集数据时&#xff0c;需要注意数据的真实性、完整性和可靠性。同时&#xff0c;需要考虑如何将不同渠道的数据进行整合和标准化&#xff0c;以便后…...

编程日记 2023/11/10 22:47:34

代码随想录算法训练营Day 47 || 198.打家劫舍、213.打家劫舍II、337.打家劫舍 III

198.打家劫舍 力扣题目链接(opens new window) 你是一个专业的小偷&#xff0c;计划偷窃沿街的房屋。每间房内都藏有一定的现金&#xff0c;影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统&#xff0c;如果两间相邻的房屋在同一晚上被小偷闯入&#xff0c;系…...

编程日记 2023/11/10 22:46:33

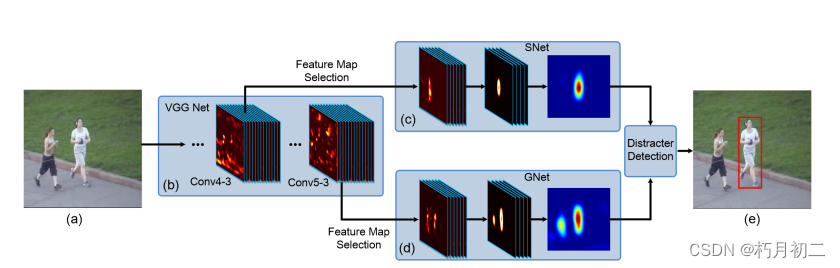
（论文阅读24/100）Visual Tracking with Fully Convolutional Networks

文献阅读笔记&#xff08;sel - CNN&#xff09; 简介 题目 Visual Tracking with Fully Convolutional Networks 作者 Lijun Wang, Wanli Ouyang, Xiaogang Wang, and Huchuan Lu 原文链接 http://202.118.75.4/lu/Paper/ICCV2015/iccv15_lijun.pdf 【DeepLearning】…...

编程日记 2023/11/10 22:45:31

第10章 文件和异常

目录 1. 从文件中读取数据1.1 读取整个文件1.2 逐行读取1.3 创建一个包含文件各行内容的列表 2. 写入文件2.1 写入空文件2.2 写入多行2.3 附加到文件 3. 异常使用try-except-else代码块 4. 存储数据使用json.dump()和json.load() 1. 从文件中读取数据 1.1 读取整个文件 with …...

编程日记 2023/11/10 22:43:28

【云栖2023】张治国：MaxCompute架构升级及开放性解读

简介&#xff1a; 本文根据2023云栖大会演讲实录整理而成&#xff0c;演讲信息如下 演讲人&#xff1a;张治国|阿里云智能计算平台研究员、阿里云MaxCompute负责人 演讲主题&#xff1a;MaxCompute架构升级及开放性解读 活动&#xff1a;2023云栖大会 MaxCompute发展经历了…...

编程日记 2023/11/10 22:41:26

【经验模态分解】4.信号由时域向频域的转换

/*** poject 经验模态分解及其衍生算法的研究及其在语音信号处理中的应用* file 傅里叶变换与小波变换* author jUicE_g2R(qq:3406291309)* * language MATLAB* EDA Base on matlabR2022b* editor Obsidian&#xff08;黑曜石笔记软件&#…...

编程日记 2023/11/10 22:40:25

STM32的M4内核在keil上面float访问就hard_fault原因

使用 Keil MDK&#xff08;Microcontroller Development Kit&#xff09;开发时&#xff0c;出现硬件故障&#xff08;hard fault&#xff09;通常是由于访问浮点数&#xff08;float&#xff09;数据类型时&#xff0c;浮点单元配置不正确或浮点单元启用导致的。以下是一些可能…...

编程日记 2023/11/10 22:39:23

MongoDB学习和应用(高效的非关系型数据库)

一丶 MongoDB简介 对于社交类软件的功能&#xff0c;我们需要对它的功能特点进行分析&#xff1a; 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具&#xff1a; mysql&#xff1a;关系型数据库&am…...

编程新知 2026/1/23 10:24:30

聊聊 Pulsar：Producer 源码解析

一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台&#xff0c;以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中&#xff0c;Producer&#xff08;生产者&#xff09; 是连接客户端应用与消息队列的第一步。生产者…...

编程新知 2026/2/5 21:34:41

YSYX学习记录（八）

C语言&#xff0c;练习0&#xff1a; 先创建一个文件夹&#xff0c;我用的是物理机&#xff1a; 安装build-essential 练习1&#xff1a; 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件&#xff0c;随机修改或删除一部分&#xff0c;之后…...

编程新知 2026/1/24 14:31:01

【机器视觉】单目测距——运动结构恢复

ps&#xff1a;图是随便找的&#xff0c;为了凑个封面 前言 在前面对光流法进行进一步改进&#xff0c;希望将2D光流推广至3D场景流时&#xff0c;发现2D转3D过程中存在尺度歧义问题&#xff0c;需要补全摄像头拍摄图像中缺失的深度信息&#xff0c;否则解空间不收敛&#xf…...

编程新知 2026/2/8 3:03:01

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序

一、开发准备 ​​环境搭建​​&#xff1a; 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 ​​项目创建​​&#xff1a; File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

编程新知 2025/9/5 12:16:40

多种风格导航菜单 HTML 实现（附源码）

下面我将为您展示 6 种不同风格的导航菜单实现&#xff0c;每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

编程新知 2026/2/2 2:49:11

Swagger和OpenApi的前世今生

Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章&#xff0c;二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑&#xff1a; &#x1f504; 一、起源与初创期&#xff1a;Swagger的诞生&#xff08;2010-2014&#xff09; 核心…...

编程新知 2026/1/25 9:08:41

Android 之 kotlin 语言学习笔记三（Kotlin-Java 互操作）

参考官方文档&#xff1a;https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java&#xff08;供 Kotlin 使用&#xff09; 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

编程新知 2026/2/8 0:33:04

学校时钟系统，标准考场时钟系统，AI亮相2025高考，赛思时钟系统为教育公平筑起“精准防线”

2025年#高考 将在近日拉开帷幕&#xff0c;#AI 监考一度冲上热搜。当AI深度融入高考&#xff0c;#时间同步 不再是辅助功能&#xff0c;而是决定AI监考系统成败的“生命线”。 AI亮相2025高考&#xff0c;40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕&#xff0c;江西、…...

编程新知 2026/2/8 22:07:52

Angular微前端架构：Module Federation + ngx-build-plus (Webpack)

以下是一个完整的 Angular 微前端示例&#xff0c;其中使用的是 Module Federation 和 npx-build-plus 实现了主应用&#xff08;Shell&#xff09;与子应用&#xff08;Remote&#xff09;的集成。 &#x1f6e0;️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

编程新知 2025/12/3 10:52:37