深度学习(生成式模型)——Classifier Guidance Diffusion
文章目录
- 前言
- 问题建模
- 条件扩散模型的前向过程
- 条件扩散模型的反向过程
- 条件扩散模型的训练目标
前言
几乎所有的生成式模型,发展到后期都需要引入"控制"的概念,可控制的生成式模型才能更好应用于实际场景。本文将总结《Diffusion Models Beat GANs on Image Synthesis》中提出的Classifier Guidance Diffusion(即条件扩散模型),其往Diffusion Model中引入了控制的概念,可以控制DDPM、DDIM生成指定类别(条件)的图片。
问题建模
本章节所有符号定义与DDPM一致,在条件 y y y下的Diffusion Model的前向与反向过程可以定义为
q ^ ( x t + 1 ∣ x t , y ) q ^ ( x t ∣ x t + 1 , y ) \begin{aligned} \hat q(x_{t+1}|x_{t},y)\\ \hat q(x_t|x_{t+1},y) \end{aligned} q^(xt+1∣xt,y)q^(xt∣xt+1,y)
只要求出上述两个概率密度函数,我们即可按条件生成图像。
我们利用 q ^ \hat q q^表示条件扩散模型的概率密度函数, q q q表示扩散模型的概率密度函数。
条件扩散模型的前向过程
对于前向过程,作者定义了以下等式
q ^ ( x 0 ) = q ( x 0 ) q ^ ( x t + 1 ∣ x t , y ) = q ( x t + 1 ∣ x t ) q ^ ( x 1 : T ∣ x 0 , y ) = ∏ t = 1 T q ^ ( x t ∣ x t − 1 , y ) \begin{aligned} \hat q(x_0)&=q(x_0)\\ \hat q(x_{t+1}|x_t,y)&=q(x_{t+1}|x_t)\\ \hat q(x_{1:T}|x_0,y)&=\prod_{t=1}^T\hat q(x_t|x_{t-1},y) \end{aligned} q^(x0)q^(xt+1∣xt,y)q^(x1:T∣x0,y)=q(x0)=q(xt+1∣xt)=t=1∏Tq^(xt∣xt−1,y)
基于上述第二行定义,可知基于条件 y y y的diffusion model的前向过程与普通的diffusion model一致,即 q ^ ( x t + 1 ∣ x t ) = q ( x t + 1 ∣ x t ) \hat q(x_{t+1}|x_t)=q(x_{t+1}|x_t) q^(xt+1∣xt)=q(xt+1∣xt)。即加噪过程与条件 y y y无关,这种定义也是合理的。
条件扩散模型的反向过程
对于反向过程,我们有
q ^ ( x t ∣ x t + 1 , y ) = q ^ ( x t , x t + 1 , y ) q ^ ( x t + 1 , y ) = q ^ ( x t , x t + 1 , y ) q ^ ( y ∣ x t + 1 ) q ^ ( x t + 1 ) = q ^ ( x t , y ∣ x t + 1 ) q ^ ( y ∣ x t + 1 ) = q ^ ( y ∣ x t , x t + 1 ) q ^ ( x t ∣ x t + 1 ) q ^ ( y ∣ x t + 1 ) (1.0) \begin{aligned} \hat q(x_t|x_{t+1},y)&=\frac{\hat q(x_t,x_{t+1},y)}{\hat q(x_{t+1},y)}\\ &=\frac{\hat q(x_t,x_{t+1},y)}{\hat q(y|x_{t+1})\hat q(x_{t+1})}\\ &=\frac{\hat q(x_t,y|x_{t+1})}{\hat q(y|x_{t+1})}\\ &=\frac{\hat q(y|x_t,x_{t+1})\hat q(x_{t}|x_{t+1})}{\hat q(y|x_{t+1})} \end{aligned}\tag{1.0} q^(xt∣xt+1,y)=q^(xt+1,y)q^(xt,xt+1,y)=q^(y∣xt+1)q^(xt+1)q^(xt,xt+1,y)=q^(y∣xt+1)q^(xt,y∣xt+1)=q^(y∣xt+1)q^(y∣xt,xt+1)q^(xt∣xt+1)(1.0)
已知条件扩散模型的前向过程与扩散模型一致,则有
q ^ ( x 1 : T ∣ x 0 ) = q ( x 1 : T ∣ x 0 ) \hat q(x_{1:T}|x_0)=q(x_{1:T}|x_0) q^(x1:T∣x0)=q(x1:T∣x0)
进而有
q ^ ( x t ) = ∫ q ^ ( x 0 , . . . , x t ) d x 0 : t − 1 = ∫ q ^ ( x 0 ) q ^ ( x 1 : t ∣ x 0 ) d x 0 : t − 1 = ∫ q ( x 0 ) q ( x 1 : t ∣ x 0 ) d x 0 : t − 1 = q ( x t ) \begin{aligned} \hat q(x_{t})&=\int \hat q(x_0,...,x_t) dx_{0:t-1}\\ &=\int \hat q(x_0)\hat q(x_{1:t}|x_0)dx_{0:t-1}\\ &=\int q(x_0)q(x_{1:t}|x_0)dx_{0:t-1}\\ &=q(x_t) \end{aligned} q^(xt)=∫q^(x0,...,xt)dx0:t−1=∫q^(x0)q^(x1:t∣x0)dx0:t−1=∫q(x0)q(x1:t∣x0)dx0:t−1=q(xt)
对于 q ^ ( x t ∣ x t + 1 ) \hat q(x_t|x_{t+1}) q^(xt∣xt+1),则有
q ^ ( x t ∣ x t + 1 ) = q ^ ( x t , x t + 1 ) q ^ ( x t + 1 ) = q ^ ( x t + 1 ∣ x t ) q ^ ( x t ) q ^ ( x t + 1 ) = q ( x t + 1 ∣ x t ) q ( x t ) q ( x t + 1 ) = q ( x t ∣ x t + 1 ) \begin{aligned} \hat q(x_t|x_{t+1})&=\frac{\hat q(x_t,x_{t+1})}{\hat q(x_{t+1})}\\ &=\frac{\hat q(x_{t+1}|x_t)\hat q(x_{t})}{\hat q(x_{t+1})}\\ &=\frac{q(x_{t+1}|x_t)q(x_{t})}{q(x_{t+1})}\\ &=q(x_{t}|x_{t+1}) \end{aligned} q^(xt∣xt+1)=q^(xt+1)q^(xt,xt+1)=q^(xt+1)q^(xt+1∣xt)q^(xt)=q(xt+1)q(xt+1∣xt)q(xt)=q(xt∣xt+1)
对于 q ^ ( y ∣ x t , x x t + 1 ) \hat q(y|x_t,x_{x_{t+1}}) q^(y∣xt,xxt+1),我们有
q ^ ( y ∣ x t , x x t + 1 ) = q ^ ( x t + 1 ∣ x t , y ) q ^ ( y ∣ x t ) q ^ ( x t + 1 ∣ x t ) = q ^ ( x t + 1 ∣ x t ) q ^ ( y ∣ x t ) q ^ ( x t + 1 ∣ x t ) = q ^ ( y ∣ x t ) \begin{aligned} \hat q(y|x_t,x_{x_{t+1}})&=\frac{\hat q(x_{t+1}|x_t,y)\hat q(y|x_t)}{\hat q(x_{t+1}|x_t)}\\ &=\frac{\hat q(x_{t+1}|x_t)\hat q(y|x_t)}{\hat q(x_{t+1}|x_t)}\\ &=\hat q(y|x_t) \end{aligned} q^(y∣xt,xxt+1)=q^(xt+1∣xt)q^(xt+1∣xt,y)q^(y∣xt)=q^(xt+1∣xt)q^(xt+1∣xt)q^(y∣xt)=q^(y∣xt)
因此式1.0为
q ^ ( x t ∣ x t + 1 , y ) = q ^ ( y ∣ x t , x t + 1 ) q ^ ( x t ∣ x t + 1 ) q ^ ( y ∣ x t + 1 ) = q ^ ( y ∣ x t ) q ( x t ∣ x t + 1 ) q ^ ( y ∣ x t + 1 ) \begin{aligned} \hat q(x_t|x_{t+1},y)&=\frac{\hat q(y|x_t,x_{t+1})\hat q(x_{t}|x_{t+1})}{\hat q(y|x_{t+1})}\\ &=\frac{\hat q(y|x_t)q(x_{t}|x_{t+1})}{\hat q(y|x_{t+1})} \end{aligned} q^(xt∣xt+1,y)=q^(y∣xt+1)q^(y∣xt,xt+1)q^(xt∣xt+1)=q^(y∣xt+1)q^(y∣xt)q(xt∣xt+1)
由于在反向过程中, x t + 1 x_{t+1} xt+1是已知的,因此 q ^ ( y ∣ x t + 1 ) \hat q(y|x_{t+1}) q^(y∣xt+1)也可看成已知值,设其倒数为 Z Z Z,则有
q ^ ( x t ∣ x t + 1 , y ) = Z q ^ ( y ∣ x t ) q ( x t ∣ x t + 1 ) \begin{aligned} \hat q(x_t|x_{t+1},y) = Z\hat q(y|x_t)q(x_{t}|x_{t+1}) \end{aligned} q^(xt∣xt+1,y)=Zq^(y∣xt)q(xt∣xt+1)
取log可得
log q ^ ( x t ∣ x t + 1 , y ) = log Z + log q ^ ( y ∣ x t ) + log q ^ ( x t ∣ x t + 1 ) (1.1) \begin{aligned} \log \hat q(x_{t}|x_{t+1},y)=\log Z+\log \hat q(y|x_t)+\log \hat q(x_t|x_{t+1})\tag{1.1} \end{aligned} logq^(xt∣xt+1,y)=logZ+logq^(y∣xt)+logq^(xt∣xt+1)(1.1)
设 q ^ ( x t ∣ x t + 1 ) = N ( μ t , ∑ t 2 ) \hat q(x_t|x_{t+1})=\mathcal N(\mu_t,\sum_t^2) q^(xt∣xt+1)=N(μt,∑t2),则有
log q ^ ( x t ∣ x t + 1 ) = − 1 2 ( x t − μ t ) T ( ∑ t ) − 1 ( x t − μ t ) + C (1.2) \log \hat q(x_{t}|x_{t+1})=-\frac{1}{2}(x_t-\mu_t)^T({\sum}_t)^{-1}(x_t-\mu_t)+C\tag{1.2} logq^(xt∣xt+1)=−21(xt−μt)T(∑t)−1(xt−μt)+C(1.2)
对于 log q ^ ( y ∣ x t ) \log \hat q(y|x_t) logq^(y∣xt),在 x t = μ t x_t=\mu_t xt=μt处做泰勒展开,则有
log q ^ ( y ∣ x t ) ≈ log q ^ ( y ∣ x t ) ∣ x t = μ t + ( x t − μ t ) ∇ x t log q ^ ( y ∣ x t ) ∣ x t = μ t = C 1 + ( x t − μ t ) g (1.3) \begin{aligned} \log \hat q(y|x_t) &\approx \log \hat q(y|x_t)|_{x_t=\mu_t}+(x_t-\mu_t)\nabla_{x_t}\log\hat q(y|x_t)|_{x_t=\mu_t}\\ &=C_1+(x_t-\mu_t)g \end{aligned}\tag{1.3} logq^(y∣xt)≈logq^(y∣xt)∣xt=μt+(xt−μt)∇xtlogq^(y∣xt)∣xt=μt=C1+(xt−μt)g(1.3)
其中 g = ∇ x t log q ^ ( y ∣ x t ) ∣ x t = μ t g=\nabla_{x_t}\log\hat q(y|x_t)|_{x_t=\mu_t} g=∇xtlogq^(y∣xt)∣xt=μt,结合式1.1、1.2、1.3,有
log q ^ ( x t ∣ x t + 1 , y ) ≈ C 1 + ( x t − μ t ) g + log Z − 1 2 ( x t − μ t ) T ( ∑ t ) − 1 ( x t − μ t ) + C = ( x t − μ t ) g − 1 2 ( x t − μ t ) T ( ∑ t ) − 1 ( x t − μ t ) + C 2 = − 1 2 ( x t − μ t − ∑ t g ) T ( ∑ t ) − 1 ( x t − μ t − ∑ t g ) + C 3 \begin{aligned} \log \hat q(x_{t}|x_{t+1},y)&\approx C_1+(x_t-\mu_t)g+\log Z-\frac{1}{2}(x_t-\mu_t)^T(\sum{_t})^{-1}(x_t-\mu_t)+C\\ &=(x_t-\mu_t)g-\frac{1}{2}(x_t-\mu_t)^T(\sum{_t})^{-1}(x_t-\mu_t)+C_2\\ &=-\frac{1}{2}(x_t-\mu_t-\sum{_t} g)^T(\sum{_t})^{-1}(x_t-\mu_t-\sum{_t}g)+C_3 \end{aligned} logq^(xt∣xt+1,y)≈C1+(xt−μt)g+logZ−21(xt−μt)T(∑t)−1(xt−μt)+C=(xt−μt)g−21(xt−μt)T(∑t)−1(xt−μt)+C2=−21(xt−μt−∑tg)T(∑t)−1(xt−μt−∑tg)+C3
最终有
q ^ ( x t ∣ x t + 1 , y ) ≈ N ( μ t + ∑ t g , ( ∑ t ) 2 ) g = ∇ x t log q ^ ( y ∣ x t ) ∣ x t = μ t (1.4) \begin{aligned} \hat q(x_t|x_{t+1},y)\approx \mathcal N(\mu_t+{\sum}_{t}g,({\sum}_t)^2)\\ g=\nabla_{x_t}\log\hat q(y|x_t)|_{x_t=\mu_t} \end{aligned}\tag{1.4} q^(xt∣xt+1,y)≈N(μt+∑tg,(∑t)2)g=∇xtlogq^(y∣xt)∣xt=μt(1.4)
为了获得 ∇ x t log q ^ ( y ∣ x t ) \nabla_{x_t}\log\hat q(y|x_t) ∇xtlogq^(y∣xt),Classifier Guidance Diffusion在训练好的Diffusion model的基础上额外训练了一个分类头。
假设 x t ≈ μ t x_t \approx\mu_t xt≈μt,则Classifier Guidance Diffusion的反向过程为:

其中 p ϕ ( y ∣ x t ) = q ^ ( y ∣ x t ) p_ \phi(y|x_t)=\hat q(y|x_t) pϕ(y∣xt)=q^(y∣xt), s s s为一个超参数。
式1.4有个问题,当方差 ∑ \sum ∑取值为0时, ∑ ∇ x t log q ^ ( y ∣ x t ) {\sum}\nabla_{x_t}\log\hat q(y|x_t) ∑∇xtlogq^(y∣xt)取值将为0,无法控制生成指定条件的图像。因此式1.4不适用于DDIM等确定性采样的扩散模型。
在推导DDIM的采样公式前,我们先了解一下用Tweedie方法做参数估计的流程。
Tweedie方法主要用于指数族概率分布的参数估计,而高斯分布属于指数族概率分布,自然也适用。假设有一批样本 z z z,则利用样本 z z z估计高斯分布 N ( Z ; μ , ∑ 2 ) \mathcal N(Z;\mu,{\sum}^2) N(Z;μ,∑2)的均值 μ \mu μ的公式为
E [ μ ∣ z ] = z + ∑ 2 ∇ z log p ( z ) (1.5) E[\mu|z]=z+{\sum}^2\nabla_z\log p(z)\tag{1.5} E[μ∣z]=z+∑2∇zlogp(z)(1.5)
已知DDPM、DDIM的前向过程有
q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) (1.6) q(x_t|x_0)=\mathcal N(x_t;\sqrt{\bar \alpha_t}x_0,(1-\bar\alpha_t)\mathcal I)\tag{1.6} q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)(1.6)
结合式1.5、1.6可得
α ˉ t x 0 = x t + ( 1 − α ˉ t ) ∇ x t log p ( x t ) \begin{aligned} \sqrt{\bar \alpha_t}x_0=x_t+(1-\bar\alpha_t)\nabla_{x_t}\log p(x_t) \end{aligned} αˉtx0=xt+(1−αˉt)∇xtlogp(xt)
进而有
x t = α ˉ t x 0 − ( 1 − α ˉ t ) ∇ x t log p ( x t ) (1.7) x_t=\sqrt{\bar \alpha_t}x_0-(1-\bar\alpha_t)\nabla_{x_t}\log p(x_t)\tag{1.7} xt=αˉtx0−(1−αˉt)∇xtlogp(xt)(1.7)
设 ϵ t \epsilon_t ϵt服从标准正态分布,则从式1.6可知
x t = α ˉ t x 0 + 1 − α ˉ t ϵ t (1.8) x_t=\sqrt{\bar \alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon_t\tag{1.8} xt=αˉtx0+1−αˉtϵt(1.8)
结合式1.7、1.8,则有
∇ x t log p ( x t ) = − 1 1 − α ˉ t ϵ t (1.9) \nabla_{x_t}\log p(x_t)=-\frac{1}{\sqrt{1-\bar\alpha_t}}\epsilon_t\tag{1.9} ∇xtlogp(xt)=−1−αˉt1ϵt(1.9)
已知DDIM的采样公式为
x t − 1 = α ˉ t − 1 x t − 1 − α ˉ t ϵ θ ( x t ) α ˉ t + 1 − α ˉ t − δ t 2 ϵ θ ( x t ) (2.0) x_{t-1}=\sqrt{\bar \alpha_{t-1}}\frac{x_t-\sqrt{1-\bar \alpha_t}\epsilon_\theta(x_t)}{\sqrt{\bar\alpha_t}}+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_\theta(x_t)\tag{2.0} xt−1=αˉt−1αˉtxt−1−αˉtϵθ(xt)+1−αˉt−δt2ϵθ(xt)(2.0)
结合式1.9、2.0可将DDIM的采样公式转变为
x t − 1 = α ˉ t − 1 x t − 1 − α ˉ t ( − 1 − α ˉ t ∇ x t log p ( x t ) ) α ˉ t + 1 − α ˉ t − δ t 2 ( − 1 − α ˉ t ∇ x t log p ( x t ) ) (2.1) x_{t-1}=\sqrt{\bar \alpha_{t-1}}\frac{x_t-\sqrt{1-\bar \alpha_t}(-\sqrt{1-\bar\alpha_t}\nabla_{x_t}\log p(x_t))}{\sqrt{\bar\alpha_t}}+\sqrt{1-\bar\alpha_{t}-\delta_t^2}(-\sqrt{1-\bar\alpha_t}\nabla_{x_t}\log p(x_t))\tag{2.1} xt−1=αˉt−1αˉtxt−1−αˉt(−1−αˉt∇xtlogp(xt))+1−αˉt−δt2(−1−αˉt∇xtlogp(xt))(2.1)
我们只需要将其中的 ∇ x t log p ( x t ) \nabla_{x_t}\log p(x_t) ∇xtlogp(xt)替换为 ∇ x t log p ( x t ∣ y ) \nabla_{x_t}\log p(x_t|y) ∇xtlogp(xt∣y),即可引入条件 y y y来控制DDIM的生成过程,利用贝叶斯定理,我们有
log p ( x t ∣ y ) = log p ( y ∣ x t ) + log p ( x t ) − log p ( y ) ∇ x t log p ( x t ∣ y ) = ∇ x t log p ( y ∣ x t ) + ∇ x t log p ( x t ) − ∇ x t log p ( y ) = ∇ x t log p ( y ∣ x t ) + ∇ x t log p ( x t ) = ∇ x t log p ( y ∣ x t ) − 1 1 − α ˉ t ϵ t (2.2) \begin{aligned} \log p(x_t|y)&=\log p(y|x_t)+\log p(x_t)-\log p(y)\\ \nabla_{x_t}\log p(x_t|y)&=\nabla_{x_t}\log p(y|x_t)+\nabla_{x_t}\log p(x_t)-\nabla_{x_t}\log p(y)\\ &=\nabla_{x_t}\log p(y|x_t)+\nabla_{x_t}\log p(x_t)\\ &=\nabla_{x_t}\log p(y|x_t)-\frac{1}{\sqrt{1-\bar\alpha_t}}\epsilon_t \end{aligned}\tag{2.2} logp(xt∣y)∇xtlogp(xt∣y)=logp(y∣xt)+logp(xt)−logp(y)=∇xtlogp(y∣xt)+∇xtlogp(xt)−∇xtlogp(y)=∇xtlogp(y∣xt)+∇xtlogp(xt)=∇xtlogp(y∣xt)−1−αˉt1ϵt(2.2)
则有
− 1 − α ˉ t ∇ x t log p ( x t ∣ y ) = ϵ t − 1 − α ˉ t ∇ x t log p ( y ∣ x t ) (2.3) -\sqrt{1-\bar\alpha_t}\nabla_{x_t}\log p(x_t|y)=\epsilon_t-\sqrt{1-\bar\alpha_t}\nabla_{x_t}\log p(y|x_t)\tag{2.3} −1−αˉt∇xtlogp(xt∣y)=ϵt−1−αˉt∇xtlogp(y∣xt)(2.3)
至此,我们可以得到DDIM的采样流程为

对于DDIM等确定性采样的扩散模型,其应在训练好的Diffusion model的基础上额外训练了一个分类头,从而转变为Classifier Guidance Diffusion。
条件扩散模型的训练目标
注意到 q ^ ( x t ∣ x t + 1 ) = q ( x t ∣ x t + 1 ) \hat q(x_t|x_{t+1})=q(x_t|x_{t+1}) q^(xt∣xt+1)=q(xt∣xt+1),并且上述的推导过程并没有改变 q ( x t ∣ x t + 1 ) 、 q ( x t + 1 ∣ x t ) q(x_t|x_{t+1})、q(x_{t+1}|x_t) q(xt∣xt+1)、q(xt+1∣xt)的形式,因此Classifier Guidance Diffusion的训练目标与DDPM、DDIM是一致的,都可以拟合训练数据。
相关文章:

深度学习(生成式模型)——Classifier Guidance Diffusion
文章目录 前言问题建模条件扩散模型的前向过程条件扩散模型的反向过程条件扩散模型的训练目标 前言 几乎所有的生成式模型,发展到后期都需要引入"控制"的概念,可控制的生成式模型才能更好应用于实际场景。本文将总结《Diffusion Models Beat …...
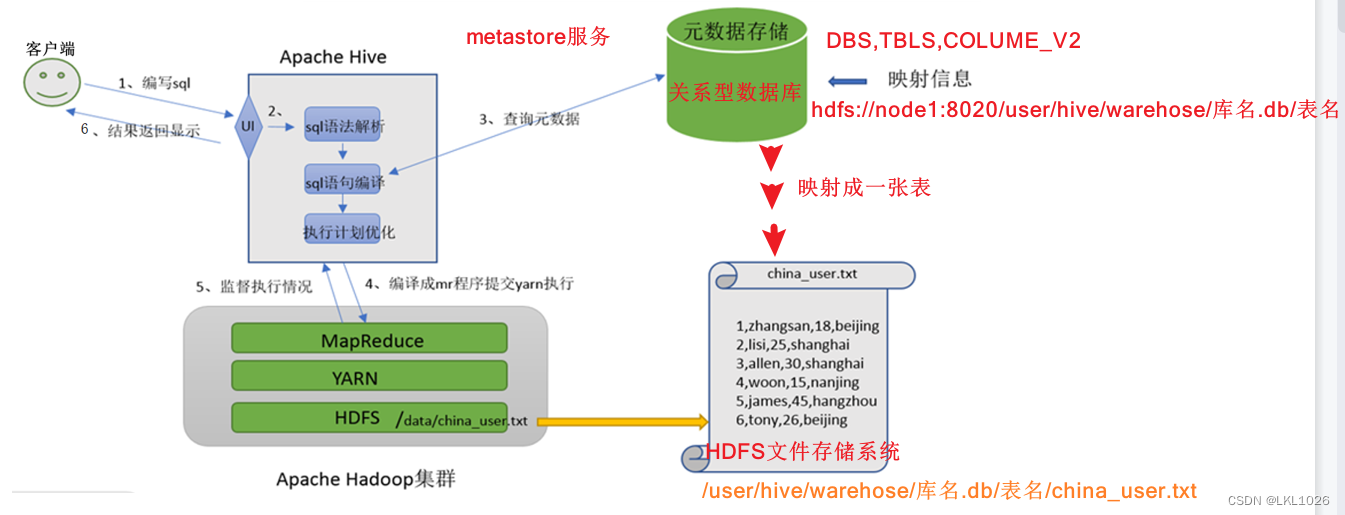
Hadoop架构、Hive相关知识点及Hive执行流程
Hadoop架构 Hadoop由三大部分组成:HDFS、MapReduce、yarn HDFS:负责数据的存储 其中包括: namenode:主节点,用来分配任务给从节点 secondarynamenode:副节点,辅助主节点 datanode:从节点&#x…...

P1529 [USACO2.4] 回家 Bessie Come Home 题解
文章目录 题目描述输入格式输出格式样例样例输入样例输出 提示完整代码 题目描述 现在是晚餐时间,而母牛们在外面分散的牧场中。 Farmer John 按响了电铃,所以她们开始向谷仓走去。 你的工作是要指出哪只母牛会最先到达谷仓(在给出的测试数…...
)
Python语法基础(条件语句 循环语句 函数 切片及索引)
目录 条件语句关键字与C对照注意 循环语句while 循环语句while else 循环语句for 循环语句range() 函数 for else 循环语句循环控制语句练习:打印乘法表 函数函数定义及调用函数值传递和引用传递多返回值参数类型位置参数默认参数关键字参数可变数量的参数可变数量的…...

Debian 9 Stretch APT问题
Debian 9 Stretch APT问题 flyfish 操作系统 Debian 9 Stretch 错误提示 使用sudo apt update错误提示 Ign:1 http://mirrors.aliyun.com/debian stretch InRelease Ign:2 http://mirrors.aliyun.com/debian-security stretch/updates InRelease Ign:3 http://mirrors.al…...
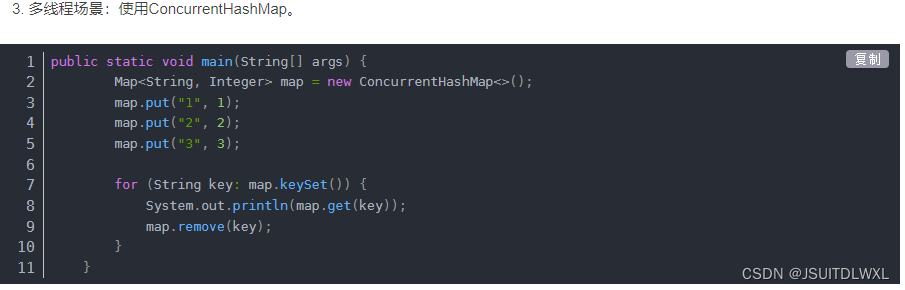
遍历List集合和Map进行修改和删除报java.util.ConcurrentModificationException错误详解
一、异常产生 当我们使用foreach迭代一个ArrayList或者HashMap时,如果尝试对集合做一些修改操作(例如删除元素或新增),可能会抛出java.util.ConcurrentModificationException的异常。 javapublic static void main(String[] args)…...

Android从一个APP跳转到另外一个APP
1、从当前APP去全新启动另外一个目标APP(非覆盖同一个进程): 启动另外一个目标APP(非覆盖原来APP的方式) 1、当前APP加入获取权限声明:(不加人权限检查,没法启动目标app࿰…...

我的创作纪念日——创作者2年
机缘 我最初使用CSDN估计是在2014年左右,当时还在读研,除了在当时比较有名的BBS例如小木虫上进行学术交流外,我发现很多问题百度后,都会转到CSDN,而且文章内容颇为专业,很多问题也都有专业的回答ÿ…...
)
大数据之LibrA数据库系统告警处理(ALM-12032 ommdba用户或密码即将过期)
告警解释 系统每天零点开始,每8小时检测当前系统中ommdba用户和密码是否过期,如果用户或密码即将在15天内过期,则发送告警。 当系统中ommdba用户过期的期限修改或密码重置,告警恢复。 告警属性 告警ID 告警级别 可自动清除 …...

C_3练习题
一、单项选择题(本大题共20小题,每小题2分,共40分。在每小题给出的四个备选项中,选出一个正确的答案,并将所选项前的字母填写在答题纸的相应位置上。) 1.下列叙述中正确的是()。 A.用C程序实现的算法必须要有输入和输出操作 B.用C程序实现的…...

CentOS7 安装Jenkins 2.414.3 详细教程
目录 1、前提条件硬件软件-java11安装 2、安装jenkins3、启动jenkins配置用户和用户组配置JAVA_HOME 4、配置Jenkins一直处于启动状态5、测试Jenkins是否可以访问以及配置6、访问Jenkins系统 1、前提条件 硬件 内存 4G ; 硬盘 20G 软件-java11安装 上传文件jdk-11.0.21_lin…...

chatglm3-6b记录问答对
# 打开文件,第二个参数是打开文件的模式,a代表追加,也就是说,打开这个文件之后直接定位到文件的末尾 file open(chatlog.txt, "a") # 写入数据 file.write(ask:prompt_text\n) file.write(response:response\n) # 关闭文件 fil…...

k8s ingress 代理 mysql 3306端口
helm 安装 ingress-nginx helm upgrade --install ingress-nginx ingress-nginx \--repo https://kubernetes.github.io/ingress-nginx \--namespace ingress-nginx --create-namespace执行命令 kubectl apply -f https://raw.githubusercontent.com/kubernetes/ingress-ngin…...

Informix管理共享内存
1、查看共享内存使用情况 [informixREHL4 ~]$ onstat -g seg IBM Informix Dynamic Server Version 11.50.UC4 -- On-Line -- Up 00:38:21 -- 144144 Kbytes Segment Summary: id key addr size ovhd class blkused blkfree 393226 …...
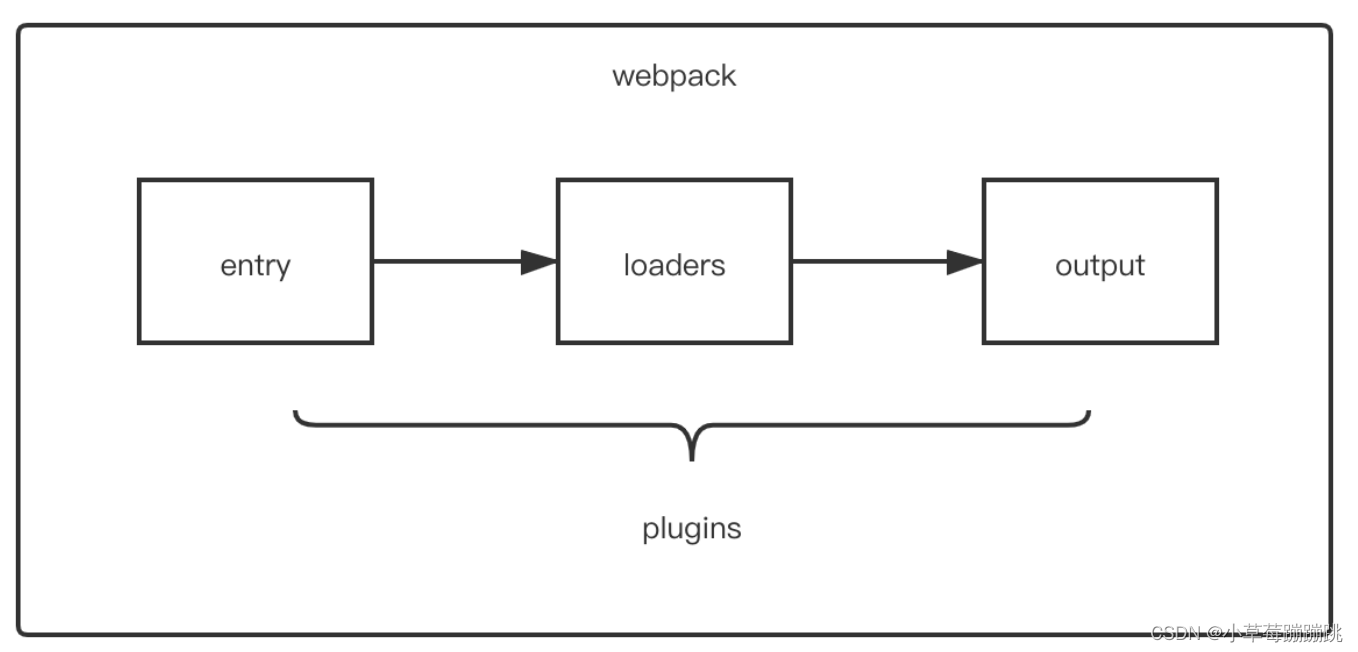
Webpack 中 Plugin 的作用是什么?常用 plugin 有哪些?
说说webpack中常见的Plugin?解决了什么问题?- 题目详情 - 前端面试题宝典 1、plugin 的作用 Plugin 是一种计算机应用程序,它和主应用程序互相交互,以提供特定的功能。 是一种遵循一定规范的应用程序接口编写出来的程序&#…...

CSRF(跨站请求伪造)攻击演示
目录 CSRF(跨站请求伪造)攻击演示CSRF 是什么CSRF 演示项目代码CSRF 演示过程服务启动演示 CSRF(跨站请求伪造)攻击演示 CSRF 是什么 CSRF(Cross-Site Request Forgery)跨站请求伪造,是一种网络安全攻击,其目标是利用被攻击者在…...
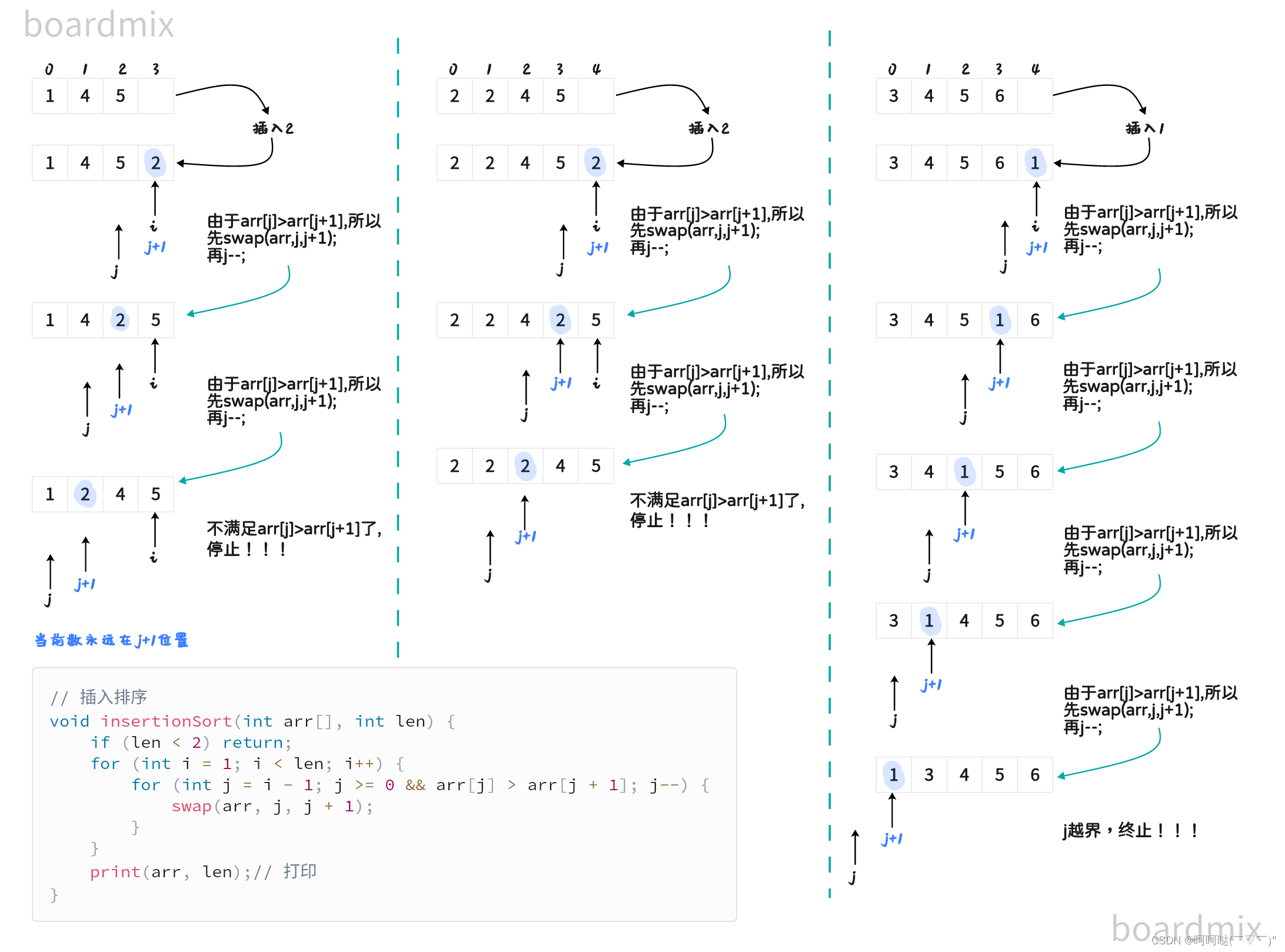
图解三傻排序 选择排序、冒泡排序、插入排序
(1)选择排序 // 交换 void swap(int arr[], int i, int j) {int tmp arr[i];arr[i] arr[j];arr[j] tmp; }// 选择排序 void selectionSort(int arr[],int len) {if (len < 2) return;for (int minIndex, i 0; i < len - 1; i) {minIndex i;f…...
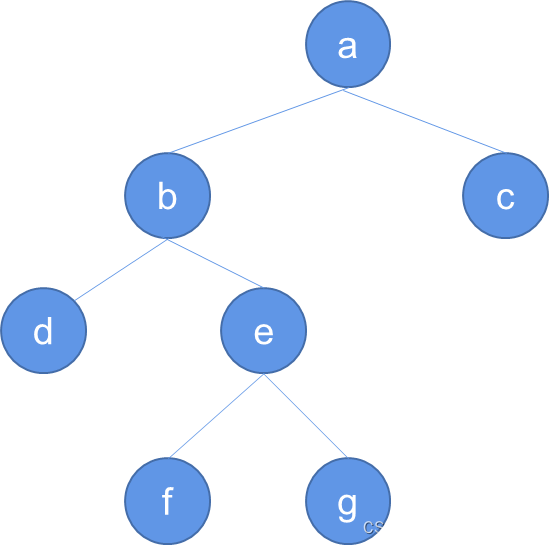
【数据结构】树与二叉树(六):二叉树的链式存储
文章目录 5.1 树的基本概念5.1.1 树的定义5.1.2 森林的定义5.1.3 树的术语5.1.4 树的表示 5.2 二叉树5.2.1 二叉树1. 定义2. 特点3. 性质引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。引理5.2:高度为k的二叉…...
)
后端Java日常实习生面试(2023年11月10日)
面试岗位为:Java 后端开发实习生 面试时长:30分钟 面试时间:2023年11月10日 首先介绍一下项目吧 这里介绍时有一个失误,没有主动把屏幕共享给打开,因为我在面试之前已经在 processon 上画好了项目的流程图…...

使用iperf3在macOS上进行网络性能测试
iperf3是一个用于测量网络性能的工具,它可以帮助你了解两台服务器之间的带宽和延迟。本博客将指导你在macOS上安装iperf3,并展示如何连接服务器进行网络性能测试。 步骤1:安装Homebrew 如果你尚未安装Homebrew,可以通过以下步骤…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...

Shell 解释器 bash 和 dash 区别
bash 和 dash 都是 Unix/Linux 系统中的 Shell 解释器,但它们在功能、语法和性能上有显著区别。以下是它们的详细对比: 1. 基本区别 特性bash (Bourne-Again SHell)dash (Debian Almquist SHell)来源G…...

第2课 SiC MOSFET与 Si IGBT 静态特性对比
2.1 输出特性对比 2.2 转移特性对比 2.1 输出特性对比 器件的输出特性描述了当温度和栅源电压(栅射电压)为某一具体数值时,漏极电流(集电极电流...

SeaweedFS S3 Spring Boot Starter
SeaweedFS S3 Spring Boot Starter 源码特性环境要求快速开始1. 添加依赖2. 配置文件3. 使用方式方式一:注入服务类方式二:使用工具类 API 文档SeaweedFsS3Service 主要方法SeaweedFsS3Util 工具类方法 配置参数运行测试构建项目注意事项集成应用更多项目…...
