数据分析实战 | 线性回归——女性身高与体重数据分析
目录
一、数据集及分析对象
二、目的及分析任务
三、方法及工具
四、数据读入
五、数据理解
六、数据准备
七、模型训练
八、模型评价
九、模型调参
十、模型预测
实现回归分析类算法的Python第三方工具包比较常用的有statsmodels、statistics、scikit-learn等,下面我们主要采用statsmodels。
一、数据集及分析对象
CSV文件——“women.csv”。
数据集链接:https://download.csdn.net/download/m0_70452407/88519967
该数据集给出了年龄在30~39岁的15名女性的身高和体重数据,主要属性如下:
(1)height:身高
(2)weight:体重
二、目的及分析任务
理解机器学习方法在数据分析中的应用——采用简单线性回归、多项式回归方法进行回归分析。
(1)训练模型。
(2)对模型进行拟合优度评价和可视化处理,验证简单线性回归建模的有效性。
(3)采用多项式回归进行模型优化。
(4)按多项式回归模型预测体重数据。
三、方法及工具
Python语言及第三方工具包pandas、matplotlib和statsmodels。
四、数据读入
import pandas as pd
df_women=pd.read_csv("D:\\Download\\JDK\\数据分析理论与实践by朝乐门_机械工业出版社\\第3章 回归分析\\women.csv",index_col=0)五、数据理解
对数据框df_women进行探索性分析。
df_women.describe()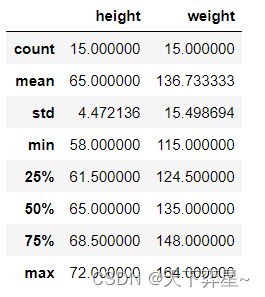
df_women.shape(15, 2)
接着,对数据库df_women进行数据可视化分析,通过调用mayplotlib.pyplot包中数据框(DataFrame)的scatter()方法绘制散点图。
import matplotlib.pyplot as plt
plt.scatter(df_women["height"],df_women["weight"])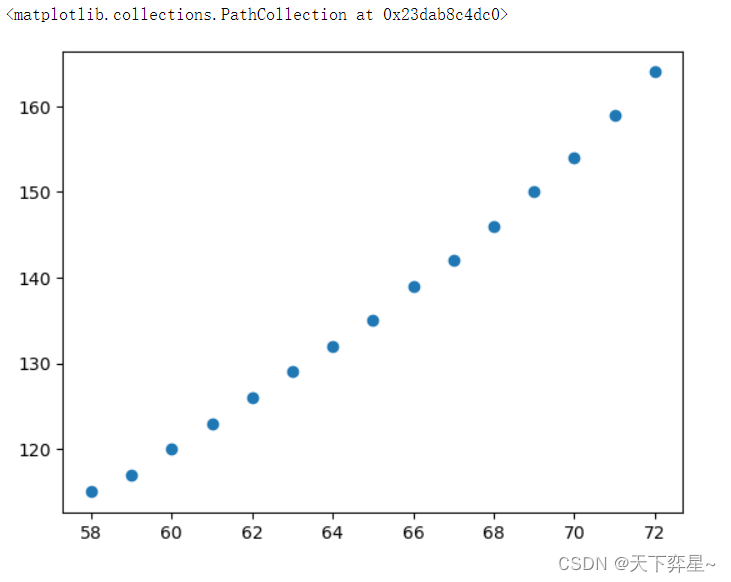
从输出结果可以看出,女性身高与体重之间的关系可以进行线性回归分析,需要进一步进行数据准备工作。
六、数据准备
进行线性回归分析之前,应准备好模型所需的特征矩阵(X)和目标向量(y)。这里我们采用Python的统计分析包statsmodel进行自动类型转换。
X=df_women['height']
y=df_women['weight']七、模型训练
以女性身高height作为自变量、体重weight作为因变量对数据进行简单线性回归建模,这里采用Python的统计分析包statsmodels中的OLS函数进行建模分析。
import statsmodels.api as smstatsmodels.OLS()方法的输入有(endog,exog,missing,hasconst)4个,其中,endog是回归中的因变量,即上述模型中的weight,exog则是自变量的值,即模型中的height。
默认情况下,statsmodels.OLS()方法不含截距项,因此应将模型中的常数项看作基为1的维度上的系数。所以,exog的输入中,最左侧的一列的数值应全为1。这里我们采用statsmodels中提供的可直接解决这一问题的方法——sm.add_constant()给X新增一列,列名为const,每行取值为1.0
X_add_const=sm.add_constant(X)
X_add_const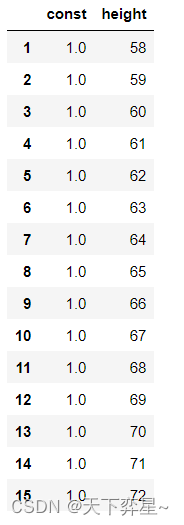
在自变量X_add_const和因变量y上使用OLS()方法进行简单线性回归。
myModel=sm.OLS(y,X_add_const)然后获取拟合结果,并调用summary()方法显示回归拟合的结果。
results=myModel.fit()
print(results.summary())OLS Regression Results ============================================================================== Dep. Variable: weight R-squared: 0.991 Model: OLS Adj. R-squared: 0.990 Method: Least Squares F-statistic: 1433. Date: Thu, 09 Nov 2023 Prob (F-statistic): 1.09e-14 Time: 18:28:09 Log-Likelihood: -26.541 No. Observations: 15 AIC: 57.08 Df Residuals: 13 BIC: 58.50 Df Model: 1 Covariance Type: nonrobust ==============================================================================coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ const -87.5167 5.937 -14.741 0.000 -100.343 -74.691 height 3.4500 0.091 37.855 0.000 3.253 3.647 ============================================================================== Omnibus: 2.396 Durbin-Watson: 0.315 Prob(Omnibus): 0.302 Jarque-Bera (JB): 1.660 Skew: 0.789 Prob(JB): 0.436 Kurtosis: 2.596 Cond. No. 982. ==============================================================================Notes: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. C:\ProgramData\Anaconda3\lib\site-packages\scipy\stats\_stats_py.py:1769: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=15warnings.warn("kurtosistest only valid for n>=20 ... continuing "
上述运行结果中第二部分的coef列所对应的const和height就是计算出的回归模型中的截距项和斜率。
除了读取回归摘要外,还可以调用params属性查看拟合结果的斜率和截距。
results.paramsconst -87.516667 height 3.450000 dtype: float64
从输出结果可以看出,回归模型中的截距项和斜率分别为-87.516667和3.450000
八、模型评价
以R^2(决定系数)作为衡量回归直线对观测值拟合程度的指标,其取值范围为[0,1],越接近1,说明“回归直线的拟合优度越好”。可以调用requared属性查看拟合结果的R^2
results.rsquared0.9910098326857505
除了决定系数等统计量,还可以通过可视化方法更直观地查看回归效果。这里我们调用matplotlib.pyplot包中的plot()方法,将回归直线与真实数据绘制在一个图中进行比较。
y_predict=results.params[0]+results.params[1]*df_women["height"]
plt.rcParams['font.family']="simHei" #汉字显示 字体设置
plt.plot(df_women["height"],df_women["weight"],"o")
plt.plot(df_women["height"],y_predict)
plt.title("女性身高与体重的线性回归分析")
plt.xlabel("身高")
plt.ylabel("体重")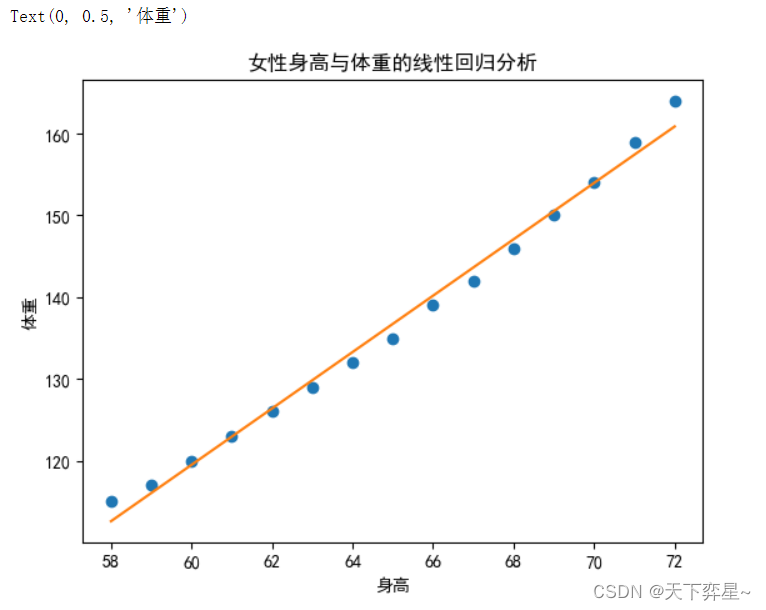
从输出结果可以看出,采用简单线性回归模型的效果还可以进一步优化,为此采取多项式回归方法进行回归分析。
九、模型调参
调用Python的统计分析包statsmodels中的OLS()方法对自变量女性身高height、因变量体重weight进行多项式回归建模。
假设因变量y与自变量X、X^2、X^3存在高元线性回归,因此在多项式分析中,特征矩阵由3部分组成,即X、X^2和X^3。通过调用numpy库的column_stack()方法创建特征矩阵X。
import numpy as np
X=np.column_stack((X,np.power(X,2),np.power(X,3)))通过sm.add_constant()方法保留多项式回归中的截距项。对自变量X_add_const和因变量y使用OLS()方法进行多项式回归。
X_add_const=sm.add_constant(X)
myModel_updated=sm.OLS(y,X_add_const)
results=myModel_updated.fit()
print(results.summary())OLS Regression Results ============================================================================== Dep. Variable: weight R-squared: 1.000 Model: OLS Adj. R-squared: 1.000 Method: Least Squares F-statistic: 1.679e+04 Date: Thu, 09 Nov 2023 Prob (F-statistic): 2.07e-20 Time: 18:46:54 Log-Likelihood: 1.3441 No. Observations: 15 AIC: 5.312 Df Residuals: 11 BIC: 8.144 Df Model: 3 Covariance Type: nonrobust ==============================================================================coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ const -896.7476 294.575 -3.044 0.011 -1545.102 -248.393 x1 46.4108 13.655 3.399 0.006 16.356 76.466 x2 -0.7462 0.211 -3.544 0.005 -1.210 -0.283 x3 0.0043 0.001 3.940 0.002 0.002 0.007 ============================================================================== Omnibus: 0.028 Durbin-Watson: 2.388 Prob(Omnibus): 0.986 Jarque-Bera (JB): 0.127 Skew: 0.049 Prob(JB): 0.939 Kurtosis: 2.561 Cond. No. 1.25e+09 ==============================================================================Notes: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. [2] The condition number is large, 1.25e+09. This might indicate that there are strong multicollinearity or other numerical problems. C:\ProgramData\Anaconda3\lib\site-packages\scipy\stats\_stats_py.py:1769: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=15warnings.warn("kurtosistest only valid for n>=20 ... continuing "
从输出结果可以看出,多项式回归模型中的截距项为-896.7476,而X、X^2、X^3对应的斜率分别为46.4108、-0.7462和0.0043
调用requared属性查看拟合结果的R^2:
results.rsquared0.9997816939979361
从决定系数的结果可以看出,多项式回归模型的效果比简单线性回归模型的效果更好。
十、模型预测
使用该多项式回归模型进行体重预测并输出预测结果。
y_predict_updated=results.predict()
y_predict_updatedarray([114.63856209, 117.40676937, 120.18801264, 123.00780722,125.89166846, 128.86511168, 131.95365223, 135.18280543,138.57808662, 142.16501113, 145.9690943 , 150.01585147,154.33079796, 158.93944911, 163.86732026])
多项式回归模型的可视化:
y_predict=(results.params[0]+results.params[1]*df_women["height"]+results.params[2]*df_women["height"]**2+results.params[3]*df_women["height"]**3)plt.plot(df_women["height"],df_women["weight"],"o")
plt.plot(df_women["height"],y_predict)
plt.title("女性身高与体重的多项式回归分析")
plt.xlabel("身高")
plt.ylabel("体重")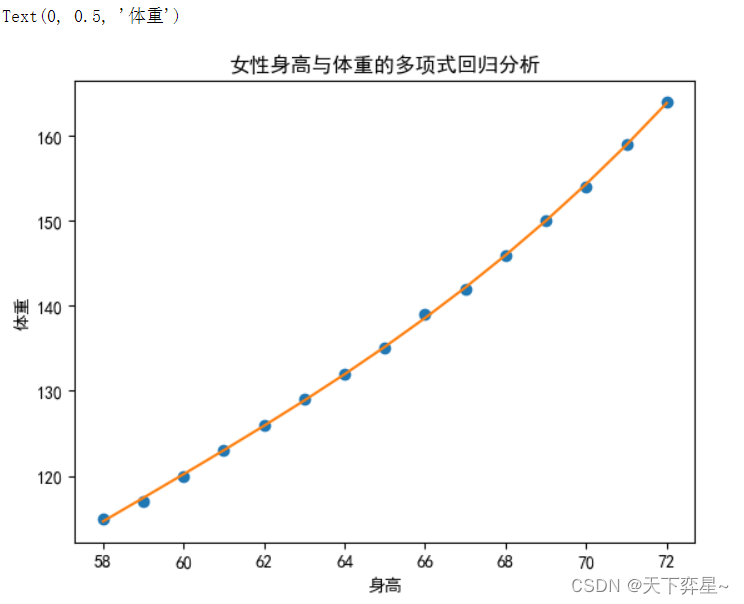
从结果可以看出,采用多项式回归后拟合效果显著提高,结果较为令人满意。
相关文章:

数据分析实战 | 线性回归——女性身高与体重数据分析
目录 一、数据集及分析对象 二、目的及分析任务 三、方法及工具 四、数据读入 五、数据理解 六、数据准备 七、模型训练 八、模型评价 九、模型调参 十、模型预测 实现回归分析类算法的Python第三方工具包比较常用的有statsmodels、statistics、scikit-learn等&#…...

python回文日期 并输出下一个ABABBABA型回文日期
题目: 输入: 输入包含一个八位整数N,表示日期 对于所有的测评用例,10000101 ≤N≤89991231,保证N是一个合法日期的8位数表示 输出: 输出两行,每行一个八位数。第一行表示下一个回文日期第二…...
Zotero拓展功能之Zotero Style
Zotero Style拓展功能 一、列: 1.简介 首先你必须知道Zotero的基本功能:右键任意一个列的名字,会弹出一个右键菜单,你可以勾选/取消勾选一个列,并且在最后有两个按钮,一个是“列设置”,一个是…...

小程序提交表单之后,清除表单form
构造表单 <form bindsubmit"bindFormSubmit"> <view class"main"><textarea name"textarea" value"{{content}}"></textarea> <button form-type"submit" type"primary" > 提交 &…...
Java程序设计实验5 | Java API应用
*本文是博主对Java各种实验的再整理与详解,除了代码部分和解析部分,一些题目还增加了拓展部分(⭐)。拓展部分不是实验报告中原有的内容,而是博主本人自己的补充,以方便大家额外学习、参考。 (解…...

自媒体项目详述
总体框架 本项目主要着手于获取最新最热新闻资讯,以微服务构架为技术基础搭建校内仅供学生教师使用的校园新媒体app。以文章为主线的核心业务主要分为如下子模块。自媒体模块实现用户创建功能、文章发布功能、素材管理功能。app端用户模块实现文章搜索、文章点赞、…...
客服呼叫中心的语音质检工作
语音质检是呼叫中心运营中必不可缺少的一个环节,呼叫中心语音质检对坐席起着直接监督的作用,也正是这种监督约束推动着客服人员不断提升自身的业务能力。 而客服呼叫中心的质检结果中还蕴藏了大量有价值的信息,可以通过日常的质检工作真正发现…...

深度解密 | 灵脉SAST 3.0最新特性曝光
一、多模智能引擎焕新 2023年6月,灵脉SAST入选国际权威咨询机构Forrester发布的《The Static Application Security Testing Landscape》报告成为全球范围内仅有的两款亚太区SAST代表产品之一。 此次3.0版本重大焕新,灵脉SAST从检测工具的灵魂核心入手…...

NowCode JZ39 数组中出现次数超过一半的数字 简单
题目 - 点击直达 1. JZ39 数组中出现次数超过一半的数字 简单1. 题目详情1. 原题链接2. 题目要求3. 基础框架 2. 解题思路1. 思路分析2. 时间复杂度3. 代码实现 1. JZ39 数组中出现次数超过一半的数字 简单 1. 题目详情 1. 原题链接 NowCode JZ39 数组中出现次数超过一半的数…...
】119 - QNX 中如何在代码中快速配置 TLMM_GPIO 或 PMIC_GPIO 中断 及 中断回调函数)
【SA8295P 源码分析 (一)】119 - QNX 中如何在代码中快速配置 TLMM_GPIO 或 PMIC_GPIO 中断 及 中断回调函数
【SA8295P 源码分析】119 - QNX 中如何在代码中快速配置 TLMM_GPIO 或 PMIC_GPIO 中断 及 中断回调函数 一、配置 TLMM GPIO15 中断示例代码二、配置 PMIC2 GPIO1 中断示例代码三、easy_irq 实现源码分析3.1 struct _easy_irq_ctx 结构体内容分析3.2 register_easy_irq_callbac…...

电大搜题:开启智能学习新时代
尊敬的读者朋友们,今天我将向您介绍一款能够让您轻松搜题、高效学习的神奇工具:电大搜题!作为湖北开放大学和广播电视大学的学习者,您一定对于繁重的课业和复杂的试题感到头疼。但是,现在有了电大搜题微信公众号&#…...
)
19、Flink 的Table API 和 SQL 中的自定义函数及示例(4)
Flink 系列文章 1、Flink 部署、概念介绍、source、transformation、sink使用示例、四大基石介绍和示例等系列综合文章链接 13、Flink 的table api与sql的基本概念、通用api介绍及入门示例 14、Flink 的table api与sql之数据类型: 内置数据类型以及它们的属性 15、Flink 的ta…...
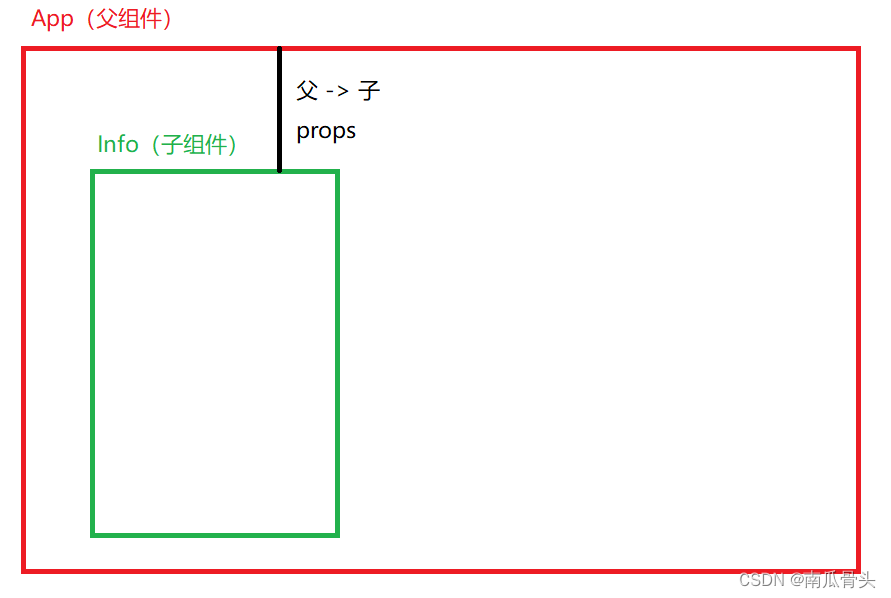
Vue23-props配置功能
Vue2&3-props配置功能 Vue2-props配置 功能:接收从其他组件传过来的数据,将数据从静态转为动态注意: 同一层组件不能使用props,必须是父组件传子组件的形式。父组件传数据,子组件接收数据。不能什么数据都接收&a…...
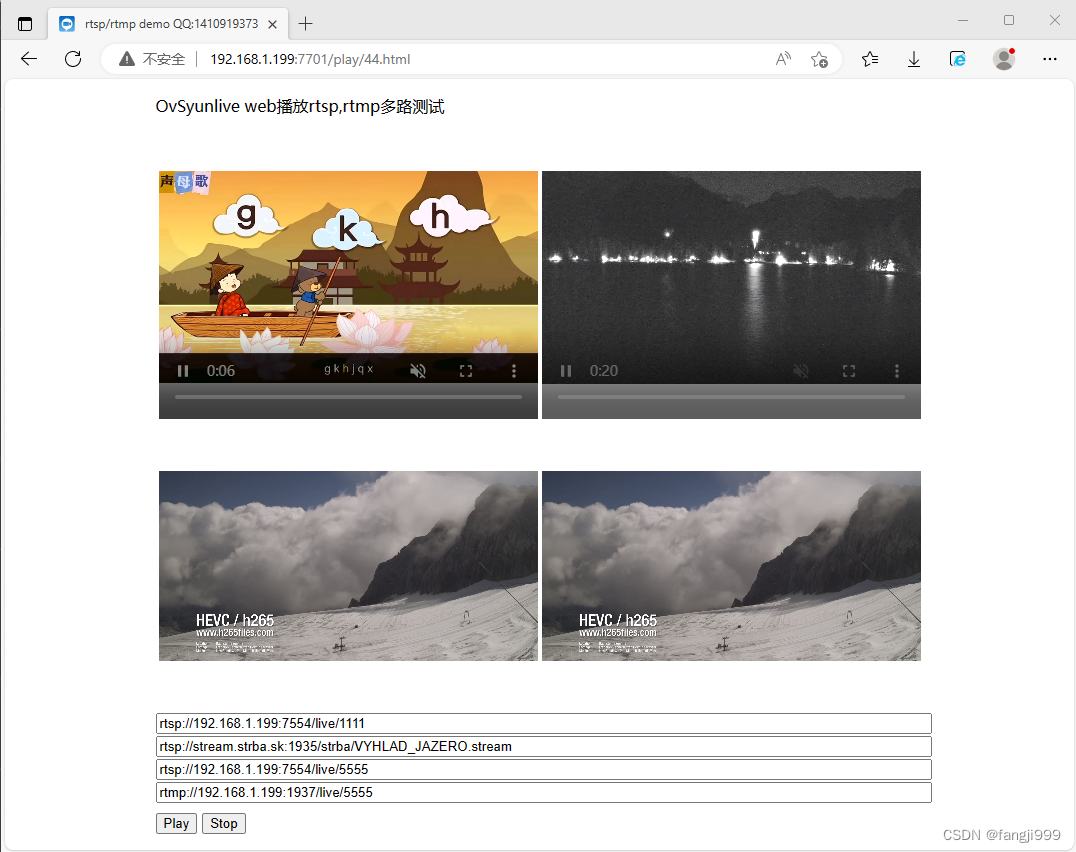
怎样使用ovsyunlive在web网页上直接播放rtsp/rtmp视频
业务中需要在网页中直接播放rtsp和rtmp视频,多方比较测试发现ovsyunlive的播放器能直接播放rtsp/rtmp视频,还是非常方便简洁,使用过程如下: 1,Windows系统在github上面下载ovsyunlive绿色包下载解压。 github地址&am…...
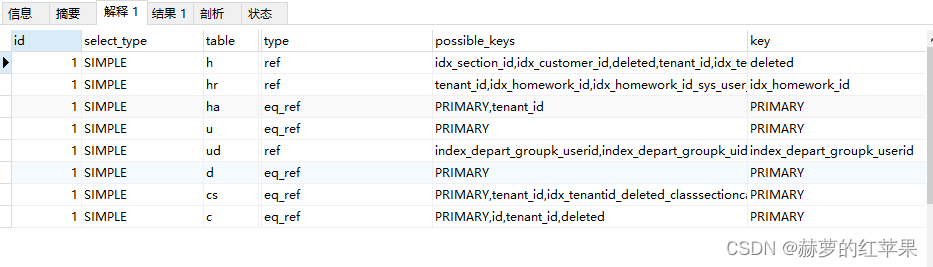
MySQL | 查询接口性能调优、编码方式不一致导致索引失效
背景 最近业务反馈,列表查询速度过慢,需要优化。 到正式环境系统去验证,发现没筛选任何条件的情况下,查询需要三十多秒,而筛选了条件之后需要13秒。急需优化。 先说结论:连表用的字段编码方式不一致导致索…...

ASUS华硕灵耀X2 Duo UX481FA(FL,FZ)_UX4000F工厂模式原装出厂Windows10系统
下载链接:https://pan.baidu.com/s/1sRHKBOyc3zu1v0qw4dSASA?pwd7nb0 提取码:7nb0 带有ASUS RECOVERY恢复功能、自带所有驱动、出厂主题壁纸、系统属性专属LOGO标志、Office办公软件、MyASUS华硕电脑管家等预装程序所需要工具:16G或以上…...
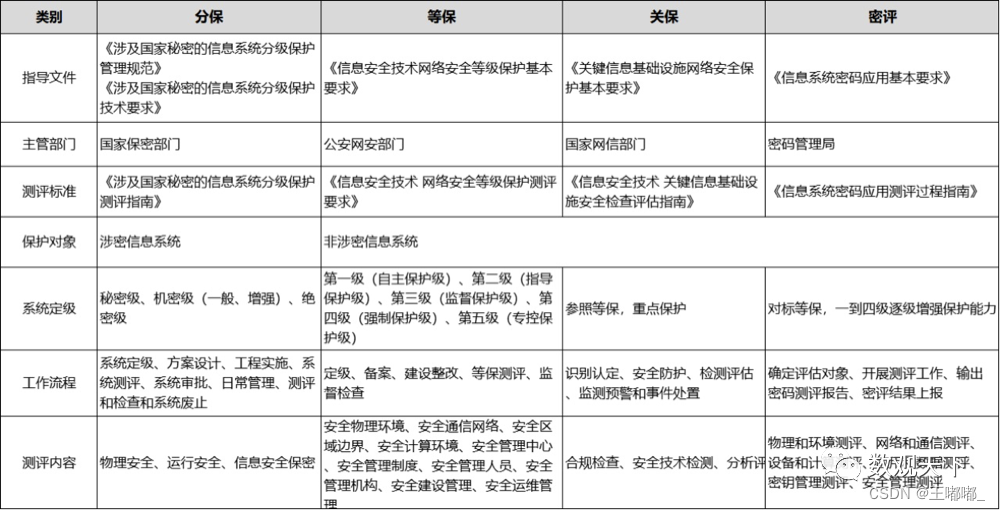
企业安全—三保一评
0x00 前言 本篇主要是讲解三保一评的基础知识,以及对为什么要进行这些内容的原因进行总结。 0x01 整体 1.概述 三保分别是,分保,等保,关保。 分保就是指涉密信息系统的建设使用单位根据分级保护管理办法和有关标准,…...

“深入理解机器学习性能评估指标:TP、TN、FP、FN、精确率、召回率、准确率、F1-score和mAP”
目录 引言 分类标准 示例:癌症检测 1. 精确率(Precision) 2. 召回率(Recall) 3. 准确率(Accuracy) 4. F1-score 5. mAP(均值平均精度) 总结与通俗解释 引言 机器…...
Linux软件包(源码包和二进制包)
Linux下的软件包众多,且几乎都是经 GPL 授权、免费开源(无偿公开源代码)的。这意味着如果你具备修改软件源代码的能力,只要你愿意,可以随意修改。 GPL,全称 General Public License,中文名称“通…...

Leetcode-394 字符串解码(不会,复习)
此题不会!!!!!!!!!!!! 题解思路:元组思想:数字[字符串],每次遇到中括号意味着要重复数字次字符串…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
