线性代数 | 矩阵运算 加减 数乘 矩阵的幂运算
文章目录
- 1 矩阵加减和数乘
- 2 矩阵与矩阵的乘法
- 2.1 相乘条件:看中间,取两头
- 2.2 相乘计算方法
- 3 矩阵的幂
- 3.1 观察归纳法
- 3.2 邻项相消法
- 3.3 化为对角
- 4 判断是否可逆(证明题或者要求求出逆矩阵)
- 4.1 直接观察
- 4.2 由定义式推得
- 4.2.1 待定系数—解方程
- 4.2.2 等价替换
- 4.2.3 因式分解
- 4.3 由性质推得
- 4.4 由矩阵行列式
- 4.5 阵的秩方阵满秩可逆,不满秩是不可逆的
- 5. 逆的性质以及求逆的方法
- 5.1 各自可逆,则乘积可逆。
- 5.2 初等变换法
- 5.3 伴随矩阵法
- 5.4 定义式法
- 6 逆的应用
- 6.1 方程组
- 7 矩阵转置
- 7.1 与行列式相联系(方阵)
- 7.2 正交矩阵
- 7.3 对称矩阵判别
《线性代数》中会有较多陌生的概念,如矩阵的逆,线性相关线性无关等,具有一定的难度。因而本系列尽量会以不同于课本的视角去学习线性代数,有些可以做类比记忆的我们会去做一些类比记忆,比如矩阵的逆类比于我们数的除法,有一些比如线性相关和无关会尽量以几何的方式直观地让大家去了解相关的内容。
《线性代数》系列重点总结线性代数相关的一些学科思想,重点方法,鉴于时间等各方面原因,对于基础的概念并不会重点阐释与总结,有基础概念不了解的比如同型矩阵去翻阅课本,课本上一定有详细的定义。所以本系列适合于初步预习之后的阅读或者在正式学习之时难点知识的参考或者在总复习之时整理相关题型方法,建立学科体系的阅读。
例题很重要,建议自己先尝试做一遍,再去看答案。同时,自己在做题过程中,遇到不会的要看看是否是下面的一些方法未掌握,或者是这些方法的综合应用,把自己不会的题总结到笔记本中,做一定的标记。
加油,希望你有所收获!!!
矩阵的运算其实类比于我们数的运算,无非也就是加减乘除。只不过在矩阵的运算中,会有更多的条件限制,比如矩阵的加减必须为同型矩阵,交换律在矩阵乘法中不满足等等。但也有很多相似的地方,比如矩阵的逆也就是我们数的除法,当矩阵行列式为零时矩阵不可逆,我们也可以联想到数如果为零的话是不能除的。
1 矩阵加减和数乘
矩阵的加减和数乘细心即可,只需要注意以下两点
(1)矩阵的加减必须为同型矩阵,行和列数要相同
(2)矩阵的数乘要区分于行列式的数乘,kA是给矩阵中的每一个元素都乘以k,而k|A|是给行列式的某一行(列)乘k
2 矩阵与矩阵的乘法
2.1 相乘条件:看中间,取两头
两个矩阵的行列数顺次排列构成四个数 a1、a2、a3、a4,只有a2=a3才能相乘,乘出来的矩阵行列分别为a1和a4 。因而我们称为看中间,取两头。好比两个朋友见面先要对个暗号,只有暗号相符(中间两个数相等)才可以计算
例1.1:
A 3 ∗ 5 ∗ B 4 ∗ 5 A_{3*5}*B_{4*5} A3∗5∗B4∗5
a1=3 a2=5 a3=4 a4=5 因而不能相乘
例1.2:
A 3 ∗ 4 ∗ B 4 ∗ 5 = C 3 ∗ 5 A_{3*4}*B_{4*5}=C_{3*5} A3∗4∗B4∗5=C3∗5
可以相乘,得到的矩阵行列分别为3和5
2.2 相乘计算方法
第一个矩阵的每一行分别去乘第二个矩阵的每一列并相加,并无难点,熟悉计算即可。
3 矩阵的幂
3.1 观察归纳法
归纳法使用于二阶三阶,阶数较小的情况,或者虽然阶数较高,但零比较多。我们可以先尝试写出二次方,三次方,观察规律,推测结果。
例1.1:设 A = ( 1 0 2 1 ) A=\begin{pmatrix}1&0\\2&1\end{pmatrix} A=(1201) 求 A n A^n An
解: A 2 = ( 1 0 4 1 ) A^2=\begin{pmatrix}1&0\\4&1\end{pmatrix} A2=(1401) A 3 = ( 1 0 6 1 ) A^3=\begin{pmatrix}1&0\\6&1\end{pmatrix} A3=(1601) 我们可以推测 A n = ( 1 0 2 n 1 ) A^n=\begin{pmatrix}1&0\\2n&1\end{pmatrix} An=(12n01)
如果是填空题直接写答案即可,如果是大题,还需要进行验证
猜想 A n = ( 1 0 2 n 1 ) A^n=\begin{pmatrix}1&0\\2n&1\end{pmatrix} An=(12n01) n=1 时成立 当n>1 时,设公式对于n-1成立,则 A n = A n − 1 A = ( 1 0 2 ( n − 1 ) 1 ) ( 1 0 2 1 ) = ( 1 0 2 n 1 ) A^n=A^{n-1}A=\begin{pmatrix}1&0\\2(n-1)&1\end{pmatrix}\begin{pmatrix}1&0\\2&1\end{pmatrix}=\begin{pmatrix}1&0\\2n&1\end{pmatrix} An=An−1A=(12(n−1)01)(1201)=(12n01)
猜想正确
3.2 邻项相消法
临项相消法使用于AB矩阵乘积形式,如果BA简单易求,结果为对角矩阵或者是一个常数或者由题目已知,则可以先算BA 即 ( A B ) n = A B A B . . . A B = A ( B A ) ( B A ) . . . B (AB)^n=ABAB...AB=A(BA)(BA)...B (AB)n=ABAB...AB=A(BA)(BA)...B
例1.2 : 设 A = ( 1 1 1 ) A=\begin{pmatrix}1\\1\\1\end{pmatrix} A= 111 B = ( 1 2 3 ) B=\begin{pmatrix}1&2&3\end{pmatrix} B=(123) 求 ( A B ) 10 (AB)^{10} (AB)10
A B = ( 1 2 3 1 2 3 1 2 3 ) AB=\begin{pmatrix}1&2&3\\1&2&3\\1&2&3\end{pmatrix} AB= 111222333 BA=6 我们发现BA比AB更容易求,则我们优先计算BA
则我们 ( A B ) 10 = A B A B . . . A B = A ( B A ) ( B A ) . . B = 6 9 A B = 6 9 ( 1 2 3 1 2 3 1 2 3 ) (AB)^{10}=ABAB...AB=A(BA)(BA)..B=6^9AB=6^9\begin{pmatrix}1&2&3\\1&2&3\\1&2&3\end{pmatrix} (AB)10=ABAB...AB=A(BA)(BA)..B=69AB=69 111222333 $
3.3 化为对角
这是我们第5章矩阵对角化的重要应用,放在这里只是为了提醒大家有这一种方法,在综合大题中,这种化为对角的方法应用还是蛮多的。化为对角矩阵为什么可行,因为对角矩阵相乘直接对角线上对应元素相乘即可
例:

A可对角化为对角矩阵B ( 5 0 0 0 − 1 0 0 0 − 1 ) \begin{pmatrix}5&0&0\\0&-1&0\\0&0&-1\end{pmatrix} 5000−1000−1 则有 P − 1 A P = B P^{-1}AP=B P−1AP=B 则 A = P B P − 1 A=PBP^{-1} A=PBP−1
A k = P B P − 1 P B P − 1 . . . P B P − 1 = P B k P − 1 A^k=PBP^{-1}PBP^{-1}...PBP^{-1}=PB^kP^{-1} Ak=PBP−1PBP−1...PBP−1=PBkP−1 而 B k = ( 5 k 0 0 0 ( − 1 ) k 0 0 0 ( − 1 ) K ) B^k=\begin{pmatrix}5^k&0&0\\0&(-1)^k&0\\0&0&(-1)^K\end{pmatrix} Bk= 5k000(−1)k000(−1)K 进而求得A的k次方
接下来就是矩阵的逆运算了!!
也就是矩阵的除法,涉及到判断是否可逆,逆的性质,逆的应用等等
4 判断是否可逆(证明题或者要求求出逆矩阵)
4.1 直接观察
某一行或某一列为零的不可逆
如果为二阶矩阵可以利用公式直接判断并计算逆矩阵
4.2 由定义式推得
如果A×B=E 则A的逆为B 有时候需要凑定义式,本质上就是转换为乘积的形式,而这其中的技巧性又很强,常见的技巧如下,抓住核心,转换为乘积形式。(K P30 例1.18)
4.2.1 待定系数—解方程
例1.1 设A,C分别为m和n阶矩阵,求证矩阵M= ( O A C B ) \begin{pmatrix}O&A\\C&B\end{pmatrix} (OCAB) 可逆,并求其逆矩阵。
解:
4.2.2 等价替换
有时候可以直接从式子中得到我们要求的量的等价关系
例1.2 设方阵A满足 A 2 − 4 A − E = 0 A^2-4A-E=0 A2−4A−E=0,证明A以及4A+E是可逆的,并求各自的逆矩阵
解: A 2 − 4 A = E A^2-4A=E A2−4A=E 即 A ( A − 4 E ) = E A(A-4E)=E A(A−4E)=E 所以 A − 1 = A − 4 E A^{-1}=A-4E A−1=A−4E 由原式可知 4 A + E = A 2 4A+E=A^2 4A+E=A2
则有 ( 4 A + E ) − 1 = ( A 2 ) − 1 (4A+E)^{-1}=(A^{2})^{-1} (4A+E)−1=(A2)−1= = ( A − 1 ) 2 =(A^{-1})^{2} =(A−1)2= ( A − 4 E ) 2 (A-4E)^2 (A−4E)2 此题中我们可以得到要求的4A+E的逆相当于求A平方的逆,进而转换为我们要求的量
4.2.3 因式分解
如果我们有 A 2 − 3 A − 4 E = E A^2-3A-4E=E A2−3A−4E=E 求A+E的逆,我们可以很轻松的想到 ( A − 4 E ) ( A + E ) = E (A-4E)(A+E)=E (A−4E)(A+E)=E,自然我们也可以求得(A+E)的逆
那如果我们把E进行一个变化如都移在右边,或者在加减E,这时候求法依然一样。
例1.3 设A为n阶矩阵,设 A 2 = A A^2=A A2=A,证明 ( A + E ) − 1 (A+E)^{-1} (A+E)−1可逆并求逆矩阵
解: A 2 − A − 2 E = − 2 E A^2-A-2E=-2E A2−A−2E=−2E ( A − 2 E ) ( A + E ) = − 2 E (A-2E)(A+E)=-2E (A−2E)(A+E)=−2E − 1 2 ( A − 2 E ) ( A + E ) = E -\frac{1}{2}(A-2E)(A+E)=E −21(A−2E)(A+E)=E 自然可以求得我们要求的答案为 − 1 2 ( A − 2 E ) -\frac{1}{2}(A-2E) −21(A−2E)
4.3 由性质推得
如果同阶方阵A1,A2…An 可逆,则我们可以知道A1 * A2 * … *An 可逆
例1.4 设A,B是同阶可逆方阵,且A+B也可逆,证明 A − 1 + B − 1 A^{-1}+B^{-1} A−1+B−1可逆,并求出逆矩阵
解: A − 1 + B − 1 = A − 1 ( B B − 1 ) + ( A − 1 A ) B − 1 = A − 1 ( A + B ) B − 1 A^{-1}+B^{-1}=A^{-1}(BB^{-1})+(A^{-1}A)B^{-1}=A^{-1}(A+B)B^{-1} A−1+B−1=A−1(BB−1)+(A−1A)B−1=A−1(A+B)B−1
因为A+B和 A − 1 A^{-1} A−1和 B − 1 B^{-1} B−1分别可逆,则原式可逆
4.4 由矩阵行列式
我们在数的除法中,零是不能做除数的,那么类比行列式,行列式为零的时候是不可逆的。
例1.5 设n阶方阵B可逆,方阵A满足 A 2 − A = B A^2-A=B A2−A=B,证明A可逆,并求其逆矩阵‘
解:因为B可逆,所以 |B|≠0 |B| =|A||A-E| 所以|A|≠0 所以A可逆
4.5 阵的秩方阵满秩可逆,不满秩是不可逆的
5. 逆的性质以及求逆的方法
5.1 各自可逆,则乘积可逆。
即如果 A 1 , A 2 , . . . , A s A_1,A_2, ... ,A_s A1,A2,...,As 可逆,那么乘积 A 1 A 2 . . . A s A_1A_2 ... A_s A1A2...As 可逆,且 ( A 1 A 2 . . . A s ) − 1 = A s − 1 . . . A 2 − 1 A 1 − 1 (A_1A_2 ... A_s)^{-1}=A_s^{-1}...A_2^{-1}A_1^{-1} (A1A2...As)−1=As−1...A2−1A1−1
例1.4 用到了这个性质
注意如果 ( A + B ) − 1 (A+B)^{-1} (A+B)−1不等于 A − 1 + B − 1 A^{-1}+B^{-1} A−1+B−1 我记得我最开始学习的时候很容易犯这个错误,其实本质上是和转置混淆了,如果转置的话是成立的, ( A + B ) T (A+B)^{T} (A+B)T= A T + B T A^{T}+B^{T} AT+BT
5.2 初等变换法
初等变换是我们求逆的最常用的方法,我们熟悉的
例1.1 设A,C分别为m和n阶矩阵,求证矩阵M= ( O A C B ) \begin{pmatrix}O&A\\C&B\end{pmatrix} (OCAB) 可逆,并求其逆矩阵。

5.3 伴随矩阵法
AA*=|A|E
5.4 定义式法
同上判断可逆时,如果AB=E ,则不仅可以判断A可逆,也可以直接得出A的逆为B
6 逆的应用
6.1 方程组
就是将我们的方程组求解转换为两个矩阵相乘,前提是A的逆好求或已知,否则的话我们还是运用后面的求方程组的方法
A x = B Ax=B Ax=B 则 $ x=A^{-1}B$
7 矩阵转置
7.1 与行列式相联系(方阵)
转置行列式值不变
7.2 正交矩阵
正交矩阵的转置等于矩阵的逆
7.3 对称矩阵判别
对称矩阵的情况下, A T = A A^T=A AT=A
例1.1 证明 A T A A^TA ATA和 A A T AA^T AAT为对称矩阵
补充题库
四-1.2.1 K P31 B 5T
四-1.2.1 K P30 例1.18
相关文章:

线性代数 | 矩阵运算 加减 数乘 矩阵的幂运算
文章目录 1 矩阵加减和数乘2 矩阵与矩阵的乘法2.1 相乘条件:看中间,取两头2.2 相乘计算方法 3 矩阵的幂3.1 观察归纳法3.2 邻项相消法3.3 化为对角 4 判断是否可逆(证明题或者要求求出逆矩阵)4.1 直接观察4.2 由定义式推得4.2.1 待…...

Linux---(五)三大工具yum、vim、gcc/g++
文章目录 一、yum工具1.Linux中安装软件的方法:2.什么是yum?3.yum源更新 二、Linux编辑器--vim1.IDE例子2.vim(1)vim的常用模式及切换模式(2)底层模式常用命令(3)插入模式常用命令(…...
网络通信TCP、UDP详解
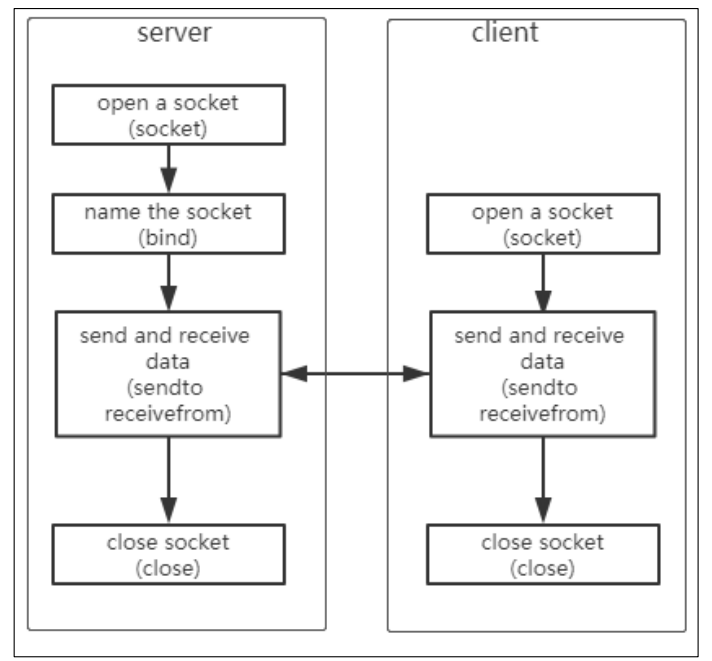
目录 IP 和端口 网络传输中的 2 个对象:server 和 client 两种传输方式:TCP/UDP TCP 和 UDP 原理上的区别 为何存在 UDP 协议 TCP/UDP 网络通信大概交互图 IP 和端口 所有的数据传输,都有三个要素 :源、目的、长度。 怎么表…...
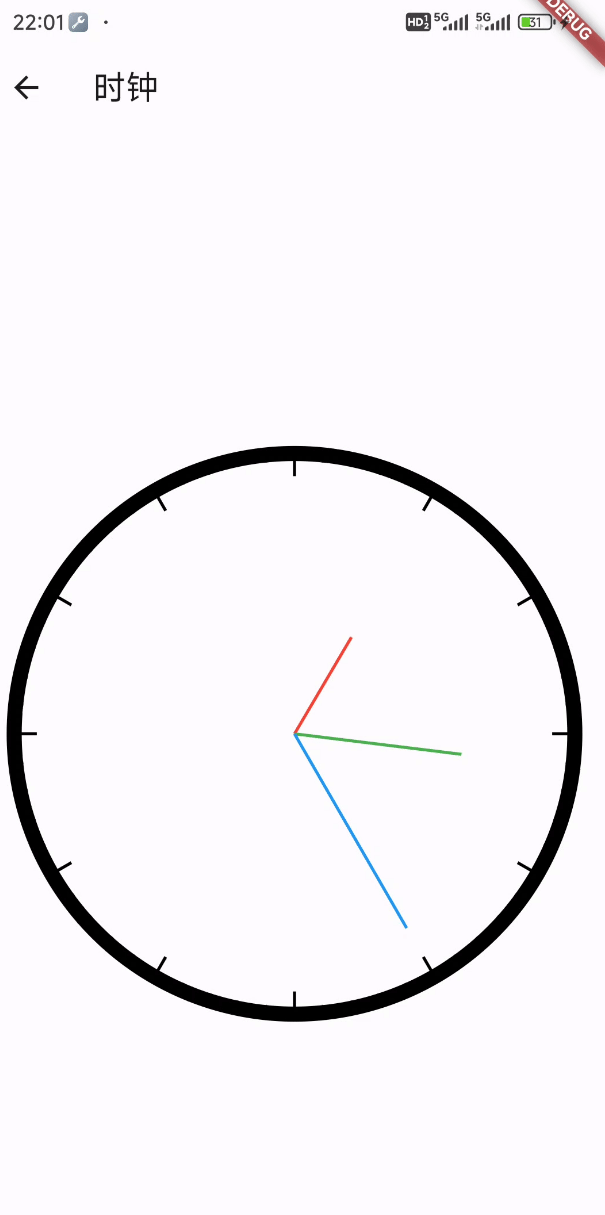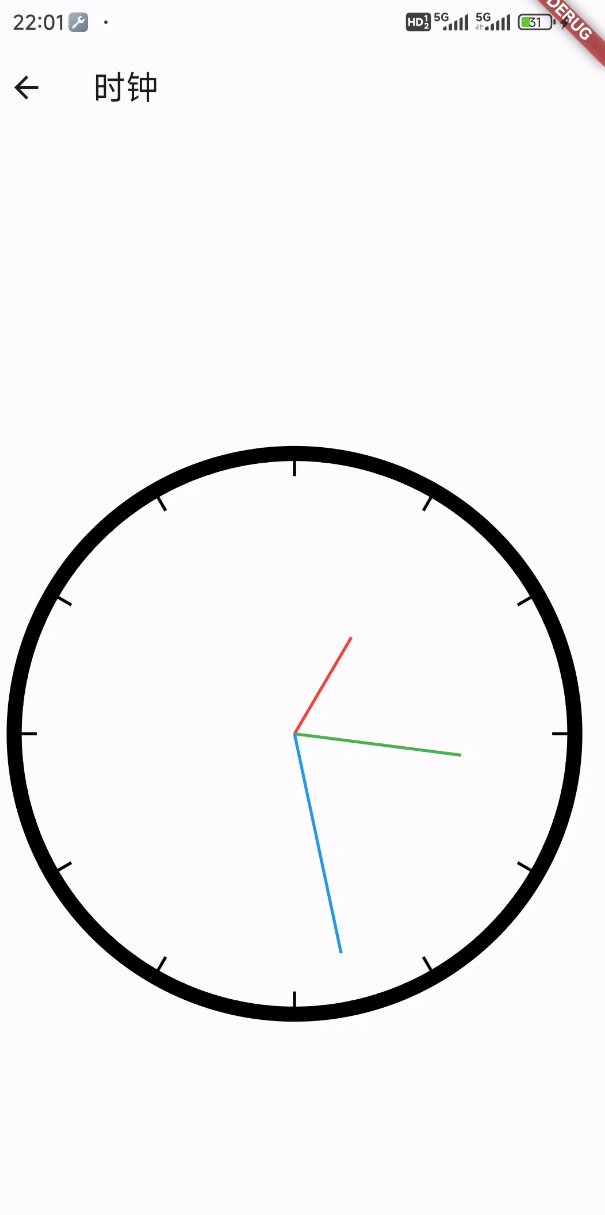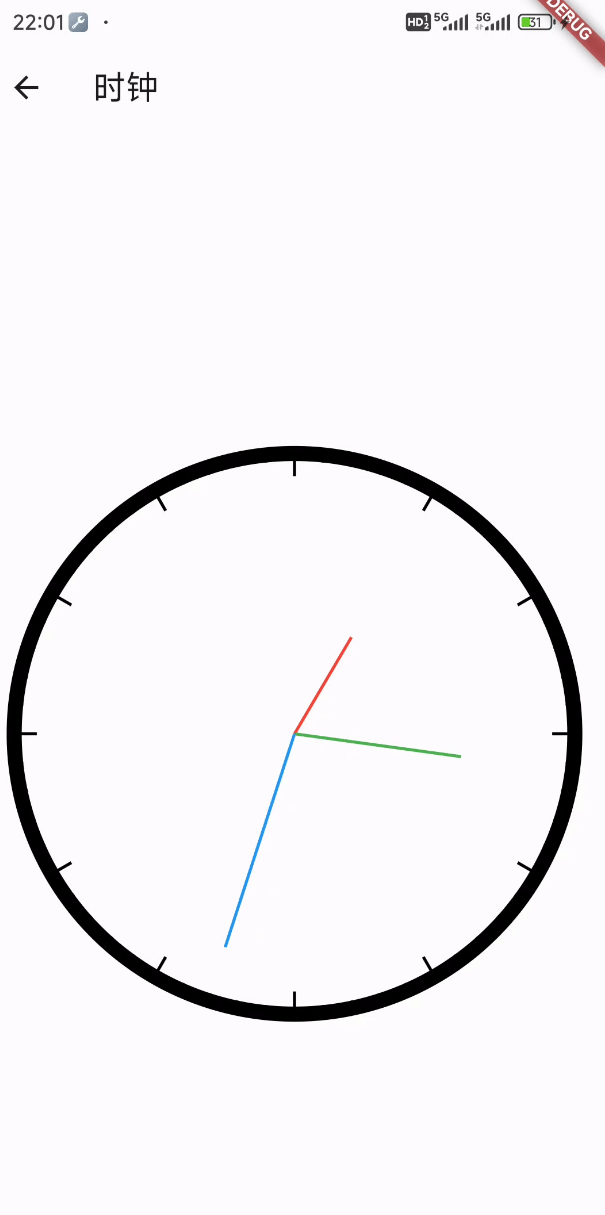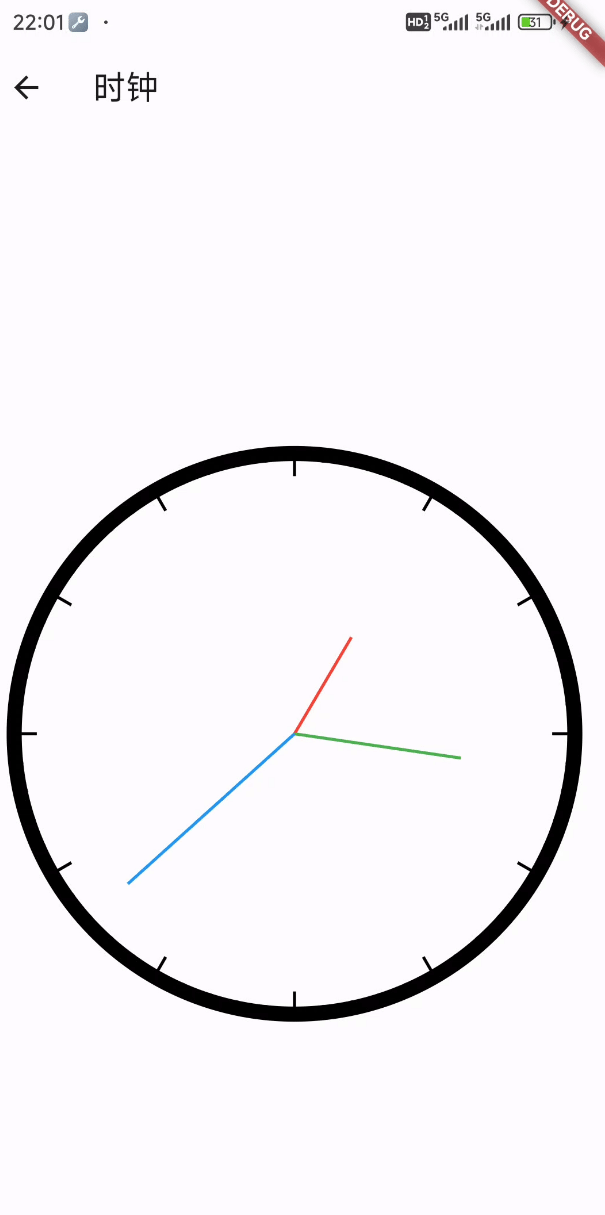
Flutter笔记:绘图示例 - 一个简单的(Canvas )时钟应用
Flutter笔记 绘图示例 - 一个简单的(Canvas )时钟应用 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_2855…...

Bard和ChatGPT的一些比较
Bard和ChatGPT的一些比较 2023.11.8版权声明:本文为博主chszs的原创文章,未经博主允许不得转载。 选择正确的自动文本生成工具对企业至关重要。本文将详细分析谷歌 Bard 和 ChatGPT 的优缺点,以帮助企业做出明智的选择。无论企业关注的是客…...
centos7安装Nexus(Maven私服)与配置使用教程
之前有位大佬问我,他说有个第三方的Jar包,在idea导出库中使用,现在要部署上线测试,要如何导进去打包。 我说,不用那么麻烦,搞个Nexus私服,将Jar上传上去,然后配置Maven的setting文件…...

Azure 机器学习 - 有关为 Azure 机器学习配置 Kubernetes 群集的参考
目录 受支持的 Kubernetes 版本和区域建议的资源计划ARO 或 OCP 群集的先决条件禁用安全增强型 Linux (SELinux)ARO 和 OCP 的特权设置 收集的日志详细信息Azure 机器学习作业与自定义数据存储连接支持的 Azure 机器学习排斥和容许最佳实践 通过 HTTP 或 HTTPS 将其他入口控制器…...
使用微信小程序控制蓝牙小车(微信小程序端)
目录 使用接口界面效果界面设计界面逻辑设计 使用接口 微信小程序官方开发文档 接口说明wx.openBluetoothAdapter初始化蓝牙模块wx.closeBluetoothAdapter关闭蓝牙模块(调用该方法将断开所有已建立的连接并释放系统资源)wx.startBluetoothDevicesDiscovery开始搜寻附近的蓝牙…...

【react hook】react hook组件中,在forEach中使用async/awati进行异步操作,为什么后面代码没有等待直接同步运行了呢?
这是因为 forEach 方法不会等待 async/await 异步操作的完成。forEach 方法是一种同步的方法,它会在每个迭代内部同步执行一个回调函数。当遇到 await 时,会立即暂停执行,但是 forEach 方法不会等待回调函数中的 await 异步操作完成ÿ…...

高斯过程回归 | GPR高斯过程回归
高斯过程回归(Gaussian Process Regression, GPR)是一种强大的非参数回归方法,它通过假设数据是从一个高斯过程中生成的来预测新的数据点。 高斯过程是一种定义在连续输入空间上的随机过程,其中任何有限集合的观测值都呈多变量高斯分布。 实现GPR的Python代码import numpy …...
[autojs]逍遥模拟器和vscode对接
第一步:启动autojs服务 第二步:去cmd查看ip地址,输入ipconfig 第三步:打开逍遥模拟器中的sutojs-左上角- 连接电脑,然后输入WLAN或者其他ip也行,根据自己电脑实际情况确认 此时vscode显示连接成功。我们写…...

Docker 安装与优化
一、安装Docker 1、关闭防火墙 systemctl stop firewalld systemctl disable firewalld setenforce 02、安装依赖包 yum -y install yum-utils device-mapper-persistent-data lvm2#解释 yum-utils #提供了yum-config-manager工具 device mapper #是linux内核中支持逻辑卷…...

Wix使用velo添加Google ads tag并在form表单提交时向谷歌发送事件
往head里加代码时,不能看谷歌的代码,要看wix的代码,不然必定踩坑 https://support.wix.com/en/article/tracking-google-ads-conversions-using-wix-custom-code 这里的代码才对,因为wix搞了个velo,这个velo很傻x&am…...
Centos配置邮件发送
在CentOS Linux上配置邮件发送 在这个指南中,我们将讨论如何配置CentOS Linux系统以通过外部邮件服务器发送电子邮件,使用自己的邮件账户进行发送。 第一步:开启SMTP授权码 首先,我们以QQ邮箱为例,需要开启SMTP授权…...

Ubuntu系统使用apt-get管理软件工具
记录一下使用Ubuntu系统的apt-get管理软件工具 先查看一下系统的版本,可以看到这里使用的是Ubuntu20.04版本,版本代号focal rootmyw:~# uname -a Linux myw 5.4.0-70-generic #78-Ubuntu SMP Fri Mar 19 13:29:52 UTC 2021 x86_64 x86_64 x86_64 GNU/L…...

带你走进Cflow (三)·控制符号类型分析
目录 编辑 1、控制符号类型 1.1 语法类 1.2 符号别名 1.3 GCC 初始化 1、控制符号类型 有人也许注意到了输出中奇怪的现象:函数_exit 丢失了,虽然它在源文件中被printdir 调用了两次。这是因为默认情况下 cflow 忽略所有的一下划线开头的符号…...
FPGA UDP RGMII 千兆以太网(3)ODDR
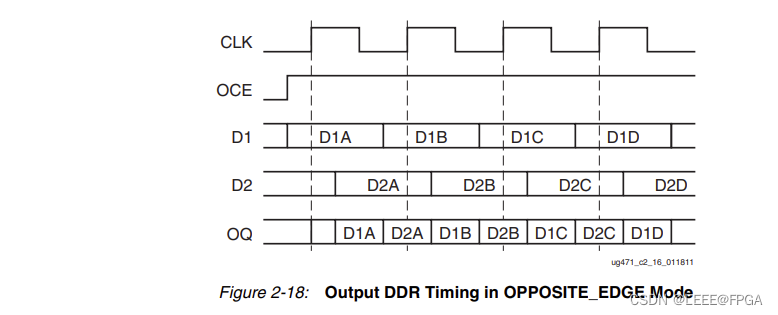
1 xilinx原语 在 7 系列 FPGA 中实现 RGMII 接口需要借助 5 种原语,分别是:IDDR、ODDR、IDELAYE2、ODELAYE2(A7 中没有)、IDELAYCTRL。其中,IDDR和ODDR分别是输入和输出的双边沿寄存器,位于IOB中。IDELAYE2和ODELAYE2,分别用于控制 IO 口输入和输出延时。同时,IDELAYE2 …...

OSG交互:选中场景模型并高亮显示
1、目的 可以在osg视图中选中指定模型实体,并高亮显示。共分为两种,一种鼠标点选,一种框选。 2、鼠标点选 2.1 功能说明 生成两组对象,一组cow对象可以被选中,另一组robot不能被选中;点击cow对象被选中高亮,点击robot被选中不高亮;点击空白处,弹出“select nothing!…...
农业大棚智能化改造升级与远程视频监管方案,助力智慧农业建设发展
一、需求分析 随着现代化技术的发展,农业大棚的智慧化也成为当前备受关注的智慧农业发展手段。利用先进的信息化手段来对农业大棚进行管理,采集和掌握作物的生长状况、作业监督、生态环境等信息数据,实现精准操作、精细管理,远程…...
P6入门:项目初始化2-项目详情之日期Date
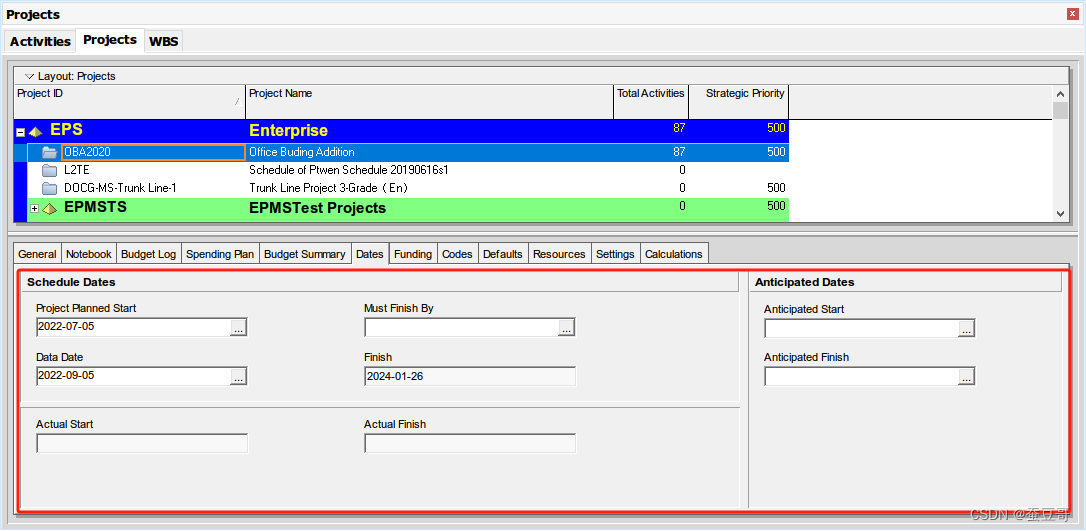
前言 使用项目详细信息查看和编辑有关所选项目的详细信息,在项目创建完成后,初始化项目是一项非常重要的工作,涉及需要设置的内容包括项目名,ID,责任人,日历,预算,资金,分类码等等&…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
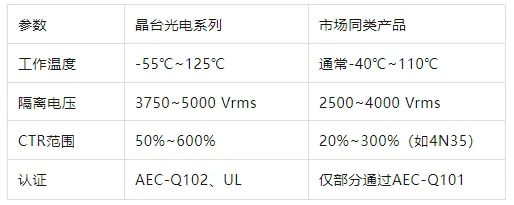
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...

