1438 绝对差不超过限制的最长连续子数组(单调队列)
题目
绝对差不超过限制的最长连续子数组
给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。
如果不存在满足条件的子数组,则返回 0 。
示例 1:
输入:nums = [8,2,4,7], limit = 4 输出:2 解释:所有子数组如下: [8] 最大绝对差 |8-8| = 0 <= 4. [8,2] 最大绝对差 |8-2| = 6 > 4. [8,2,4] 最大绝对差 |8-2| = 6 > 4. [8,2,4,7] 最大绝对差 |8-2| = 6 > 4. [2] 最大绝对差 |2-2| = 0 <= 4. [2,4] 最大绝对差 |2-4| = 2 <= 4. [2,4,7] 最大绝对差 |2-7| = 5 > 4. [4] 最大绝对差 |4-4| = 0 <= 4. [4,7] 最大绝对差 |4-7| = 3 <= 4. [7] 最大绝对差 |7-7| = 0 <= 4. 因此,满足题意的最长子数组的长度为 2 。
示例 2:
输入:nums = [10,1,2,4,7,2], limit = 5 输出:4 解释:满足题意的最长子数组是 [2,4,7,2],其最大绝对差 |2-7| = 5 <= 5 。
示例 3:
输入:nums = [4,2,2,2,4,4,2,2], limit = 0 输出:3
提示:
1 <= nums.length <= 10^51 <= nums[i] <= 10^90 <= limit <= 10^9
题解
与滑动窗口最大值类似,维护一个max队列保证队首为最大值,维护一个min队列保证队首为最小值,枚举right更新答案
class Solution {public int longestSubarray(int[] nums, int limit) {//利用两个双端队列,max从左到右单调递增,队首为最大值,min相反Deque<Integer> maxdeque = new ArrayDeque<>();Deque<Integer> mindeque = new ArrayDeque<>();int n = nums.length;int right = 0, left = 0, ans = 0;//枚举rightwhile (right < n) {while (!maxdeque.isEmpty() && nums[right] > maxdeque.peekLast()) {maxdeque.removeLast();}while (!mindeque.isEmpty() && nums[right] < mindeque.peekLast()) {mindeque.removeLast();}maxdeque.addLast(nums[right]);mindeque.addLast(nums[right]);//移动leftwhile (maxdeque.peekFirst() - mindeque.peekFirst() > limit) {//更新对内元素if (maxdeque.peekFirst() == nums[left]) {maxdeque.removeFirst();}if (mindeque.peekFirst() == nums[left]) {mindeque.removeFirst();}left++;}ans = Math.max(ans, right - left + 1);right++;}return ans;}
}相关文章:
)
1438 绝对差不超过限制的最长连续子数组(单调队列)
题目 绝对差不超过限制的最长连续子数组 给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。 如果不存在满足条件的子数组,则返…...

OpenCV入门9:图像增强和图像滤波
图像增强是一种通过对图像进行处理以改善其质量、对比度、清晰度等方面的技术。在OpenCV中,有多种图像增强的方法和函数可用。下面简要介绍一些常见的图像增强方法及其在OpenCV中的实现方式。 直方图均衡化(Histogram Equalization)ÿ…...

Pycharm常用快捷键和替换正则表达式
原生快捷键的使用: 1.CtrlF:查找 2.CtrlZ:返回上一步 3.Alt 鼠标左键选择:多行同时编辑(上、下、左、右键能够移动光标) 按住Ctrl,左键点击,定位光标 编辑过程 URL常用的替换正则表达式&am…...

C#,数值计算——函数计算,Epsalg的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// Convergence acceleration of a sequence by the algorithm.Initialize by /// calling the constructor with arguments nmax, an upper bound on the /// number of term…...

Delphi 12 重返雅典 (RAD Studio 12)
RAD Studio 12 的新功能: 以最新的平台版本为目标! RAD Studio 12 提供对 iOS 17(仅适用于 Delphi)、Android 14 和 macOS Sonoma 的官方支持。RAD Studio 12 还支持 Ubuntu 22 LTS 和 Windows Server 2022。 Delphi 源代码的多…...

手写链表C++
目录 一、链表基本概念以及注意事项 1.1 构造函数与析构函数 1.2 插入元素 1.3 重载运算符 二、小结 一、链表基本概念以及注意事项 在工作中,链表是一种常见的数据结构,可以用于解决很多实际问题。在学习中,掌握链表可以提高编程能力和…...

为什么我一直是机器视觉调机仔,为什么一定要学一门高级语言编程?
为什么我是机器视觉调机仔,为什么一定要学一门高级语言编程,以后好不好就业,待遇高不高,都是跟这项技术没关系,是跟这个技术背后的行业发展有关系。 你可以选择离机器视觉行业,也可以选择与高级语言相关…...
)
MongoDB单实例安装(Linux)
实战环境 centos7系统、64位 iptables和selinux关闭 mongodb简介 mongodb是个非关系型数据库,但操作跟关系型数据最类似。mysql是关系型数据库 mongodb是面向文档存储的非关系型数据库,数据以json的格式进行存储 mongodb可用来永久存储,也可用…...

各种业务场景调用API代理的API接口教程(附带电商平台api接口商品详情数据接入示例)
API代理的API接口在各种业务场景中具有广泛的应用,本文将介绍哪些业务场景可以使用API代理的API接口,并提供详细的调用教程和代码演示,同时,我们还将讨论在不同场景下使用API代理的API接口所带来的好处。 哪些业务场景可以使用API…...

React-hooks有哪些 包括用法是什么?
React Hooks是React 16.8版本引入的功能,它允许你在函数组件中使用状态(state)和其他React特性,而无需编写类组件。以下是一些常用的React Hooks及其用法: 1:useState:用于在函数组件中添加状态…...
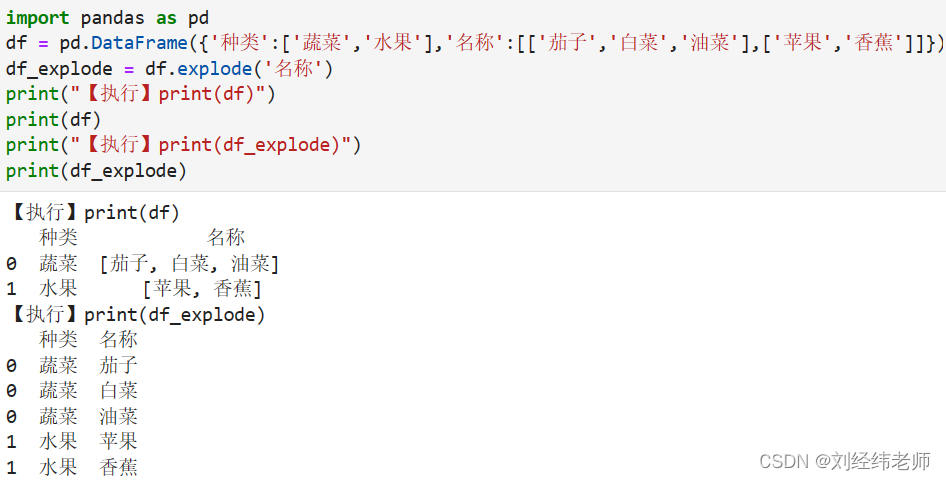
根据DataFrame指定的列该列中如果有n个不同元素则将其转化为n行显示explode()
【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 根据DataFrame指定的列 该列中如果有n个不同元素 则将其转化为n行显示 explode() 选择题 以下代码两次输出结果分别为几行? import pandas as pd df pd.DataFrame({种类:[蔬菜,水…...
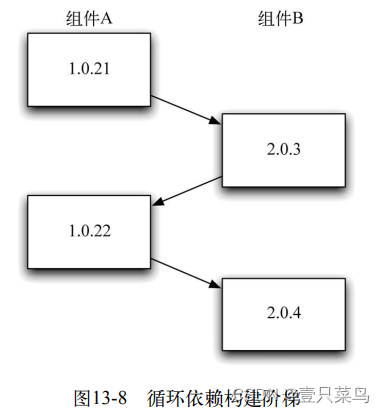
《持续交付:发布可靠软件的系统方法》- 读书笔记(十三)
持续交付:发布可靠软件的系统方法(十三) 第 13 章 组件和依赖管理13.1 引言13.2 保持应用程序可发布13.2.1 将新功能隐蔽起来,直到它完成为止13.2.2 所有修改都是增量式的13.2.3 通过抽象来模拟分支 13.3 依赖13.3.1 依赖地狱13.3…...
【Copilot】登录报错 Extension activation failed: “No auth flow succeeded.“(VSCode)
问题描述 Visual Studio Code 登录 GitHub Copilot 插件报错。 在浏览器中成功授权 GitHub 账户,返回 VSCode 后仍然报错。 [ERROR] [default] [2023-11-06T12:34:56.185Z] Extension activation failed: "No auth flow succeeded."原因分析 网络环境问…...

uboot - 驱动开发 - dw watchdog
说明 公司SOC使用的watchdog模块是新思(Synopsys)的IP。 需求 用户有时会在uboot/kernel中做些开发,新增一些功能(OTA升级等),可能会出现uboot/kernel启动崩溃甚至设备死机等问题,需要在uboo…...

【系统架构设计】架构核心知识: 2.5 软件测试、系统转换计划、系统维护
目录 一 软件测试 1 静态测试 2 动态测试 3 测试 4 集成测试的策略 二...

EXPLAIN详解(MySQL)
EXPLAIN概述 EXPLAIN语句提供MySQL如何执行语句的信息。EXPLAIN与SELECT, DELETE, INSERT, REPLACE和UPDATE语句一起工作。 EXPLAIN返回SELECT语句中使用的每个表的一行信息。它按照MySQL在处理语句时读取表的顺序列出了输出中的表。MySQL使用嵌套循环连接方法解析所有连接。…...
[PyTorch][chapter 61][强化学习-免模型学习 off-policy]
前言: 蒙特卡罗的学习基本流程: Policy Evaluation : 生成动作-状态轨迹,完成价值函数的估计。 Policy Improvement: 通过价值函数估计来优化policy。 同策略(one-policy):产生 采样轨迹的策略 和要改…...

【服务器学习】 iomanager IO协程调度模块
iomanager IO协程调度模块 以下是从sylar服务器中学的,对其的复习; 参考资料 继承自协程调度器,封装了epoll,支持为socket fd注册读写事件回调函数 IO协程调度还解决了调度器在idle状态下忙等待导致CPU占用率高的问题。IO协程调…...

前端设计模式之【迭代器模式】
文章目录 前言介绍实现接口优缺点应用场景后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:前端设计模式 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。(如果出现错误&a…...

Linux-用户与用户组,权限
1.用户组管理(以下命令需root用户执行) ①创建用户组 groupadd 用户组名 ②删除用户组 groupdel 用户组名 2.用户管理(以下命令需root用户执行) ①创建用户 useradd [-g -d] 用户名 >-g:指定用户的组,不…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...
)
后端下载限速(redis记录实时并发,bucket4j动态限速)
✅ 使用 Redis 记录 所有用户的实时并发下载数✅ 使用 Bucket4j 实现 全局下载速率限制(动态)✅ 支持 动态调整限速策略✅ 下载接口安全、稳定、可监控 🧩 整体架构概览 模块功能Redis存储全局并发数和带宽令牌桶状态Bucket4j Redis分布式限…...
Xcode 16.2 版本 pod init 报错
Xcode 版本升级到 16.2 后,项目执行 pod init 报错; ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchron…...
