使用Python从零实现多分类SVM
前言
本文将首先简要概述支持向量机及其训练和推理方程,然后将其转换为代码以开发支持向量机模型。之后然后将其扩展成多分类的场景,并通过使用Sci-kit Learn测试我们的模型来结束。
SVM概述
支持向量机的目标是拟合获得最大边缘的超平面(两个类中最近点的距离)。可以直观地表明,这样的超平面(A)比没有最大化边际的超平面(B)具有更好的泛化特性和对噪声的鲁棒性。
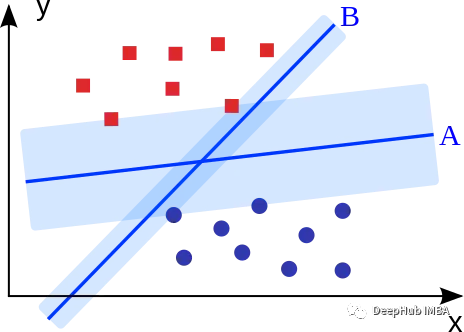
为了实现这一点,SVM通过求解以下优化问题找到超平面的W和b:
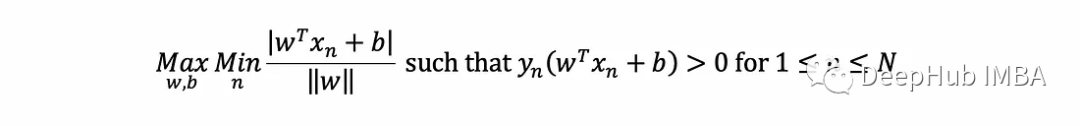
它试图找到W,b,使最近点的距离最大化,并正确分类所有内容(如y取±1的约束)。这可以被证明相当于以下优化问题:
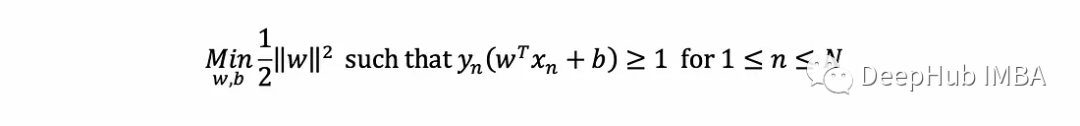
可以写出等价的对偶优化问题
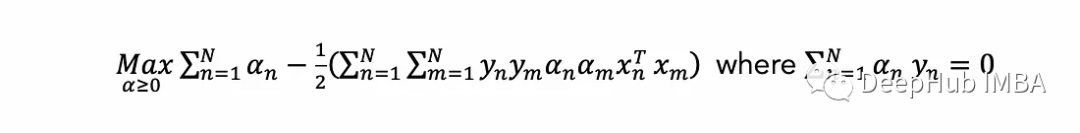
这个问题的解决方案产生了一个拉格朗日乘数,我们假设数据集中的每个点的大小为m:(α 1, α 2,…,α _n)。目标函数在α中明显是二次的,约束是线性的,这意味着它可以很容易地用二次规划求解。一旦找到解,由对偶的推导可知:
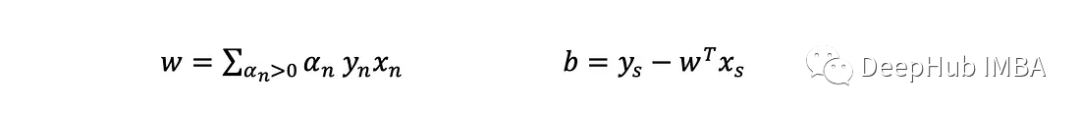
注意,只有具有α>0的点才定义超平面(对和有贡献)。这些被称为支持向量。因此当给定一个新例子x时,返回其预测y=±1的预测方程为:
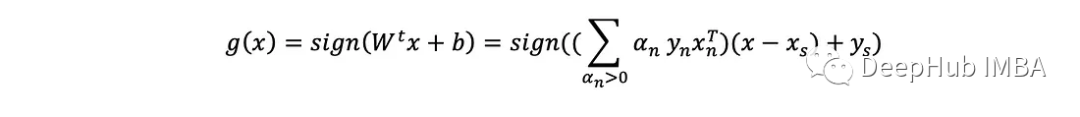
这种支持向量机的基本形式被称为硬边界支持向量机(hard margin SVM),因为它解决的优化问题(如上所述)强制要求训练中的所有点必须被正确分类。但在实际场景中,可能存在一些噪声,阻止或限制了完美分离数据的超平面,在这种情况下,优化问题将不返回或返回一个糟糕的解决方案。
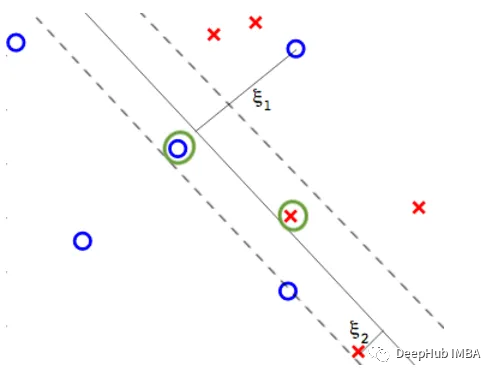
软边界支持向量机(soft margin SVM)通过引入C常数(用户给定的超参数)来适应优化问题,该常数控制它应该有多“硬”。特别地,它将原优化问题修改为:
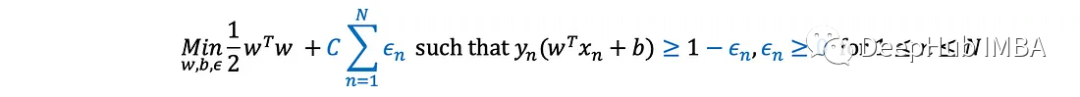
它允许每个点产生一些错误λ(例如,在超平面的错误一侧),并且通过将它们在目标函数中的总和加权C来减少它们。当C趋于无穷时(一般情况下肯定不会),它就等于硬边界。与此同时,较小的C将允许更多的“违规行为”(以换取更大的支持;例如,更小的w (w)。
可以证明,等价对偶问题只有在约束每个点的α≤C时才会发生变化。
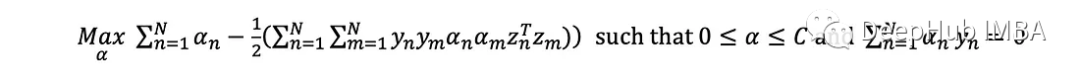
由于允许违例,支持向量(带有α>0的点)不再都在边界的边缘。任何错误的支持向量都具有α=C,而非支持向量(α=0)不能发生错误。我们称潜在错误(α=C)的支持向量为“非错误编剧支持向量”和其他纯粹的支持向量(没有违规;“边界支持向量”(0<α<C)。
这样推理方程不变:
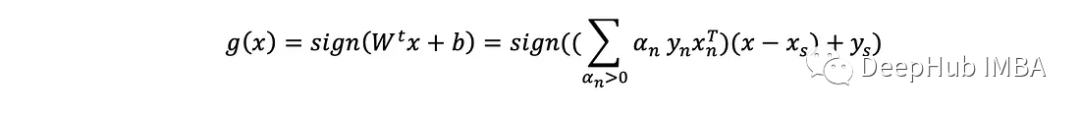
现在(xₛ,yₛ)必须是一个没有违规的支持向量,因为方程假设它在边界的边缘。
软边界支持向量机扩展了硬边界支持向量机来处理噪声,但通常由于噪声以外的因素,例如自然非线性,数据不能被超平面分离。软边界支持向量机可以用于这样的情况,但是最优解决方案的超平面,它允许的误差远远超过现实中可以容忍的误差。
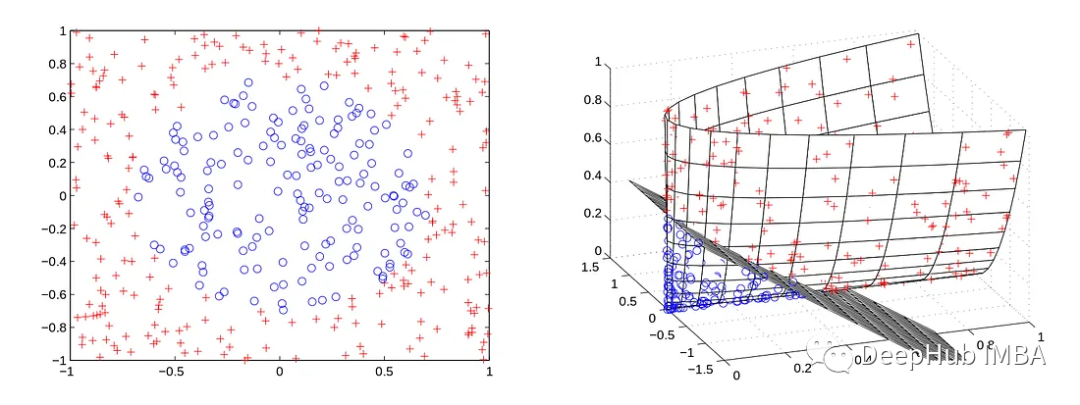
例如,在左边的例子中,无论C的设置如何,软边界支持向量机都找不到线性超平面。但是可以通过某种转换函数z=Φ(x)将数据集中的每个点x映射到更高的维度,从而使数据在新的高维空间中更加线性(或完全线性)。这相当于用z替换x得到:
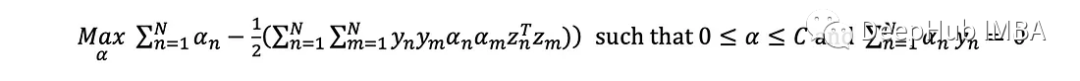
在现实中,特别是当Φ转换为非常高维的空间时,计算z可能需要很长时间。所以就出现了核函数。它用一个数学函数(称为核函数)的等效计算来取代z,并且更快(例如,对z进行代数简化)。例如,这里有一些流行的核函数(每个都对应于一些转换Φ到更高维度空间):
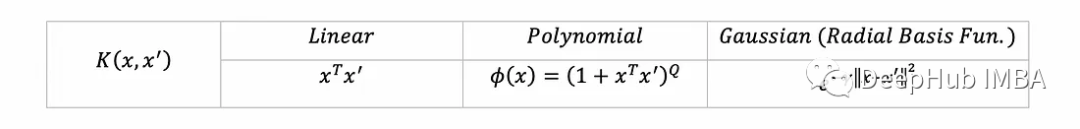
这样,对偶优化问题就变成:
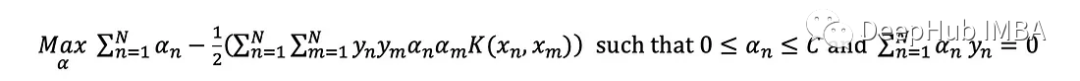
直观地,推理方程(经过代数处理后)为:
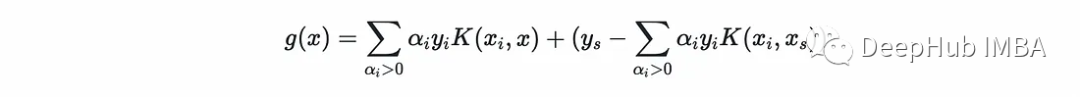
上面所有方程的完整推导,有很多相关的文章了,我们就不详细介绍了。
Python实现
对于实现,我们将使用下面这些库:
import numpy as np # for basic operations over arraysfrom scipy.spatial import distance # to compute the Gaussian kernelimport cvxopt # to solve the dual opt. problemimport copy # to copy numpy arrays定义核和SVM超参数,我们将实现常见的三个核函数:
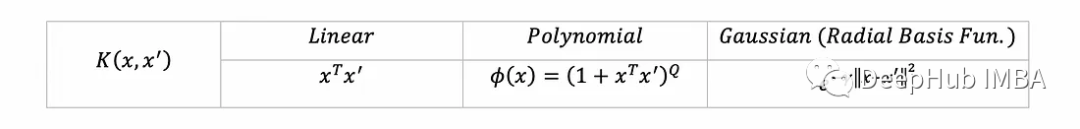
class SVM:linear = lambda x, xࠤ , c=0: x @ xࠤ.Tpolynomial = lambda x, xࠤ , Q=5: (1 + x @ xࠤ.T)**Qrbf = lambda x, xࠤ, γ=10: np.exp(-γ*distance.cdist(x, xࠤ,'sqeuclidean'))kernel_funs = {'linear': linear, 'polynomial': polynomial, 'rbf': rbf}为了与其他核保持一致,线性核采用了一个额外的无用的超参数。kernel_funs接受核函数名称的字符串,并返回相应的内核函数。
继续定义构造函数:
class SVM:linear = lambda x, xࠤ , c=0: x @ xࠤ.Tpolynomial = lambda x, xࠤ , Q=5: (1 + x @ xࠤ.T)**Qrbf = lambda x, xࠤ, γ=10: np.exp(-γ*distance.cdist(x, xࠤ,'sqeuclidean'))kernel_funs = {'linear': linear, 'polynomial': polynomial, 'rbf': rbf}def __init__(self, kernel='rbf', C=1, k=2):# set the hyperparametersself.kernel_str = kernelself.kernel = SVM.kernel_funs[kernel]self.C = C # regularization parameterself.k = k # kernel parameter# training data and support vectors (set later)self.X, y = None, Noneself.αs = None# for multi-class classification (set later)self.multiclass = Falseself.clfs = [] SVM有三个主要的超参数,核(我们存储给定的字符串和相应的核函数),正则化参数C和核超参数(传递给核函数);它表示多项式核的Q和RBF核的γ。
为了兼容sklearn的形式,我们需要使用fit和predict函数来扩展这个类,定义以下函数,并在稍后将其用作装饰器:
SVMClass = lambda func: setattr(SVM, func.__name__, func) or func拟合SVM对应于通过求解对偶优化问题找到每个点的支持向量α:
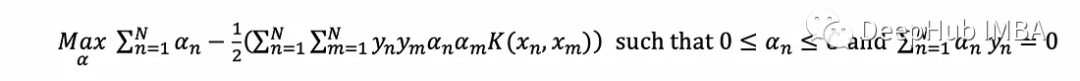
设α为可变列向量(α₁α₂…α _n);y为标签(y₁α₂…y_N)常数列向量;K为常数矩阵,其中K[n,m]计算核在(x, x)处的值。点积、外积和二次型分别基于索引的等价表达式:
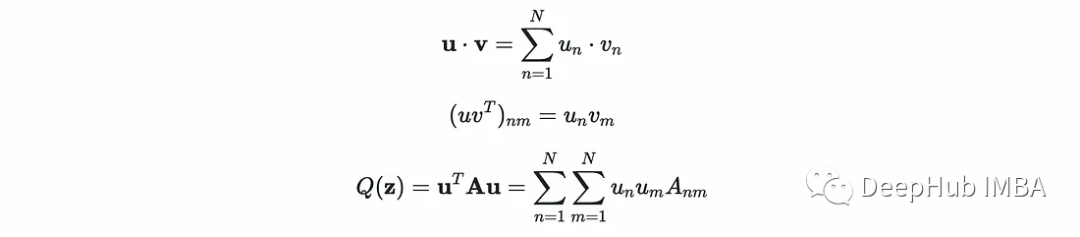
可以将对偶优化问题写成矩阵形式如下:
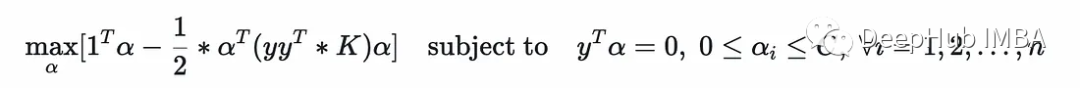
这是一个二次规划,CVXOPT的文档中解释如下:

可以只使用(P,q)或(P,q,G,h)或(P,q,G,h, A, b)等等来调用它(任何未给出的都将由默认值设置,例如1)。
对于(P, q, G, h, A, b)的值,我们的例子可以做以下比较:

为了便于比较,将第一个重写如下:
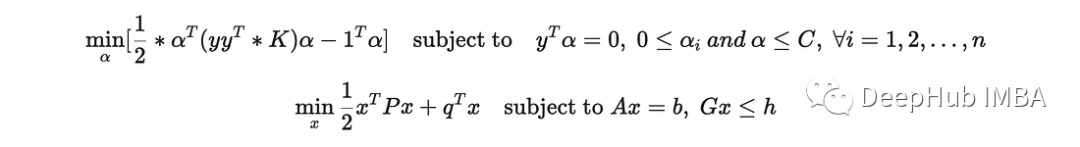
现在很明显(0≤α等价于-α≤0):

我们就可以写出如下的fit函数:
@SVMClassdef fit(self, X, y, eval_train=False):# if more than two unique labels, call the multiclass versionif len(np.unique(y)) > 2:self.multiclass = Truereturn self.multi_fit(X, y, eval_train)# if labels given in {0,1} change it to {-1,1}if set(np.unique(y)) == {0, 1}: y[y == 0] = -1# ensure y is a Nx1 column vector (needed by CVXOPT)self.y = y.reshape(-1, 1).astype(np.double) # Has to be a column vectorself.X = XN = X.shape[0] # Number of points# compute the kernel over all possible pairs of (x, x') in the data# by Numpy's vectorization this yields the matrix Kself.K = self.kernel(X, X, self.k)### Set up optimization parameters# For 1/2 x^T P x + q^T xP = cvxopt.matrix(self.y @ self.y.T * self.K)q = cvxopt.matrix(-np.ones((N, 1)))# For Ax = bA = cvxopt.matrix(self.y.T)b = cvxopt.matrix(np.zeros(1))# For Gx <= hG = cvxopt.matrix(np.vstack((-np.identity(N),np.identity(N))))h = cvxopt.matrix(np.vstack((np.zeros((N,1)),np.ones((N,1)) * self.C)))# Solve cvxopt.solvers.options['show_progress'] = Falsesol = cvxopt.solvers.qp(P, q, G, h, A, b)self.αs = np.array(sol["x"]) # our solution# a Boolean array that flags points which are support vectorsself.is_sv = ((self.αs-1e-3 > 0)&(self.αs <= self.C)).squeeze()# an index of some margin support vectorself.margin_sv = np.argmax((0 < self.αs-1e-3)&(self.αs < self.C-1e-3))if eval_train: print(f"Finished training with accuracy{self.evaluate(X, y)}")我们确保这是一个二进制问题,并且二进制标签按照支持向量机(±1)的假设设置,并且y是一个维数为(N,1)的列向量。然后求解求解(α₁α₂…α _n) 的优化问题。
使用(α₁α₂…α _n) _来获得在与支持向量对应的任何索引处为1的标志数组,然后可以通过仅对支持向量和(xₛ,yₛ)的边界支持向量的索引求和来应用预测方程。我们确实假设非支持向量可能不完全具有α=0,如果它的α≤1e-3,那么这是近似为零(CVXOPT结果可能不是最终精确的)。同样假设非边际支持向量可能不完全具有α=C。
下面就是预测的方法,预测方程为:
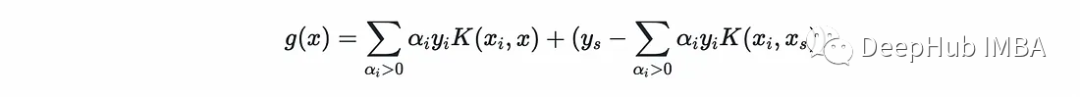
@SVMClassdef predict(self, X_t):if self.multiclass: return self.multi_predict(X_t)# compute (xₛ, yₛ)xₛ, yₛ = self.X[self.margin_sv, np.newaxis], self.y[self.margin_sv]# find support vectorsαs, y, X= self.αs[self.is_sv], self.y[self.is_sv], self.X[self.is_sv]# compute the second termb = yₛ - np.sum(αs * y * self.kernel(X, xₛ, self.k), axis=0)# compute the scorescore = np.sum(αs * y * self.kernel(X, X_t, self.k), axis=0) + breturn np.sign(score).astype(int), score我们还可以实现一个评估方法来计算精度(在上面的fit中使用)。
@SVMClassdef evaluate(self, X,y): outputs, _ = self.predict(X)accuracy = np.sum(outputs == y) / len(y)return round(accuracy, 2)最后测试我们的完整代码:
from sklearn.datasets import make_classificationimport numpy as np# Load the datasetnp.random.seed(1)X, y = make_classification(n_samples=2500, n_features=5, n_redundant=0, n_informative=5, n_classes=2, class_sep=0.3)# Test Implemented SVMsvm = SVM(kernel='rbf', k=1)svm.fit(X, y, eval_train=True)y_pred, _ = svm.predict(X)print(f"Accuracy: {np.sum(y==y_pred)/y.shape[0]}") #0.9108# Test with Scikitfrom sklearn.svm import SVCclf = SVC(kernel='rbf', C=1, gamma=1)clf.fit(X, y)y_pred = clf.predict(X)print(f"Accuracy: {sum(y==y_pred)/y.shape[0]}") #0.9108多分类SVM
我们都知道SVM的目标是二元分类,如果要将模型推广到多类则需要为每个类训练一个二元SVM分类器,然后对每个类进行循环,并将属于它的点重新标记为+1,并将所有其他类的点重新标记为-1。
当给定k个类时,训练的结果是k个分类器,其中第i个分类器在数据上进行训练,第i个分类器被标记为+1,所有其他分类器被标记为-1。
@SVMClassdef multi_fit(self, X, y, eval_train=False):self.k = len(np.unique(y)) # number of classes# for each pair of classesfor i in range(self.k):# get the data for the pairXs, Ys = X, copy.copy(y)# change the labels to -1 and 1Ys[Ys!=i], Ys[Ys==i] = -1, +1# fit the classifierclf = SVM(kernel=self.kernel_str, C=self.C, k=self.k)clf.fit(Xs, Ys)# save the classifierself.clfs.append(clf)if eval_train: print(f"Finished training with accuracy {self.evaluate(X, y)}")然后,为了对新示例执行预测,我们选择相应分类器最自信(得分最高)的类。
@SVMClassdef multi_predict(self, X):# get the predictions from all classifiersN = X.shape[0]preds = np.zeros((N, self.k))for i, clf in enumerate(self.clfs):_, preds[:, i] = clf.predict(X)# get the argmax and the corresponding scorereturn np.argmax(preds, axis=1), np.max(preds, axis=1)完整测试代码:
from sklearn.datasets import make_classificationimport numpy as np# Load the datasetnp.random.seed(1)X, y = make_classification(n_samples=500, n_features=2, n_redundant=0, n_informative=2, n_classes=4, n_clusters_per_class=1, class_sep=0.3)# Test SVMsvm = SVM(kernel='rbf', k=4)svm.fit(X, y, eval_train=True)y_pred = svm.predict(X)print(f"Accuracy: {np.sum(y==y_pred)/y.shape[0]}") # 0.65# Test with Scikitfrom sklearn.multiclass import OneVsRestClassifierfrom sklearn.svm import SVCclf = OneVsRestClassifier(SVC(kernel='rbf', C=1, gamma=4)).fit(X, y)y_pred = clf.predict(X)print(f"Accuracy: {sum(y==y_pred)/y.shape[0]}") # 0.65绘制每个决策区域的图示,得到以下图:
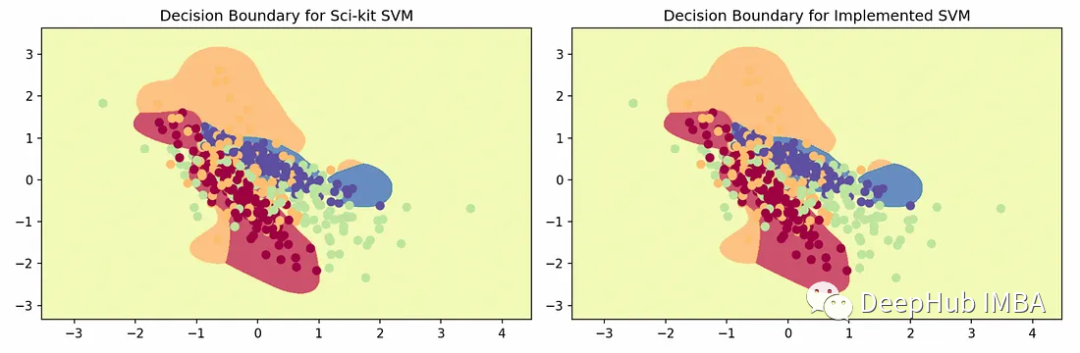
可以看到,我们的实现与Sci-kit Learn结果相当,说明在算法实现上没有问题。注意:SVM默认支持OVR(没有如上所示的显式调用),它是特定于SVM的进一步优化。
总结
我们使用Python实现了支持向量机(SVM)学习算法,并且包括了软边界和常用的三个核函数。我们还将SVM扩展到多分类的场景,并使用Sci-kit Learn验证了我们的实现。希望通过本文你可以更好的了解SVM。
相关文章:

使用Python从零实现多分类SVM
前言 本文将首先简要概述支持向量机及其训练和推理方程,然后将其转换为代码以开发支持向量机模型。之后然后将其扩展成多分类的场景,并通过使用Sci-kit Learn测试我们的模型来结束。 SVM概述 支持向量机的目标是拟合获得最大边缘的超平面(两个类中最近…...

WPF ToggleButton 主题切换动画按钮
WPF ToggleButton 主题切换动画按钮 仿造最近看到的html中的一个效果,大致思路是文章这样,感觉还可以再雕琢一下。 代码如下 XAML: <UserControl x:Class"WPFSwitch.AnimationSwitch"xmlns"http://schemas.microsoft.com/winfx/200…...

centerOS下docker 搭建IotDB集群
一、准备3台机器,IP地址依次为IP1,IP2,IP3,找一个目录下建立文件夹如下: ./data/confignode ./logs/confignode ./data/datanode ./logs/datanode二、在当前目录下建立docker-compose.yml文件,3台都要 1、…...

Vue3-Composition-API-学习笔记
01.Setup函数的体验 App.vue <template><div><h2>当前计数:{{ counter }}</h2><button click"increment">1</button><button click"decrement">-1</button></div> </template>&…...
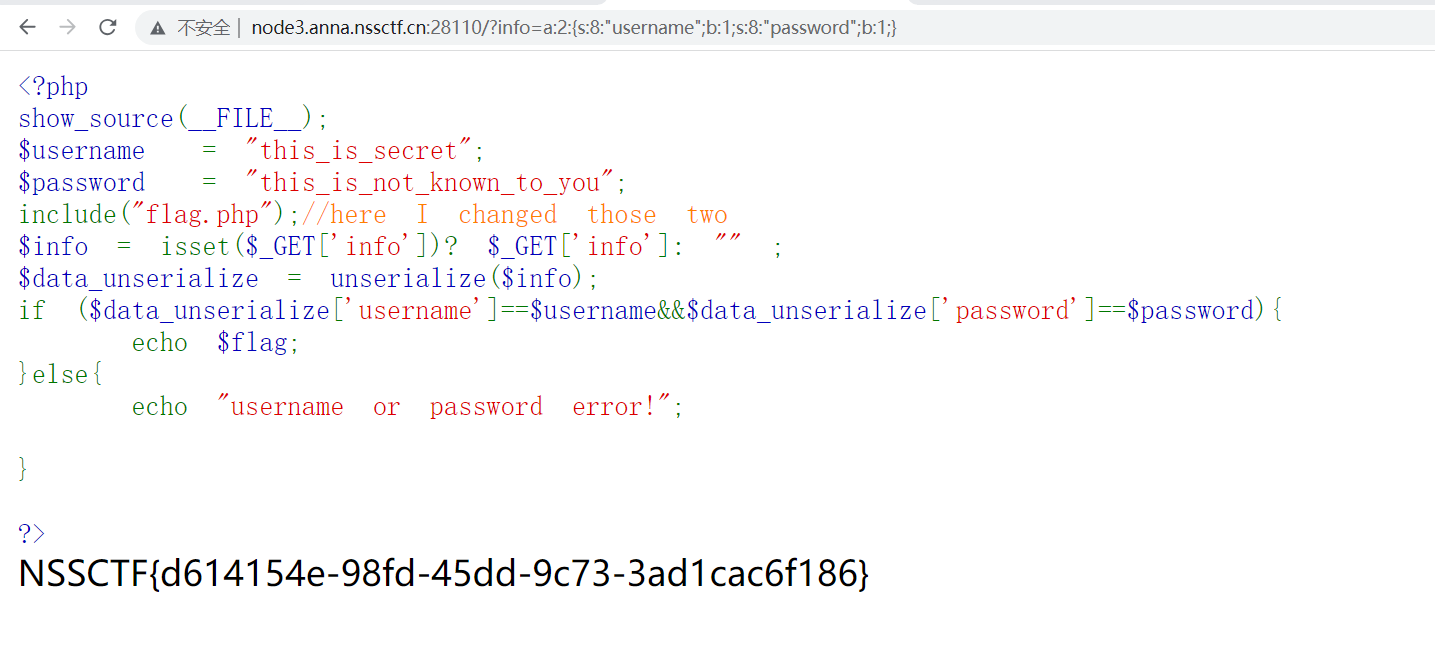
NSS [HUBUCTF 2022 新生赛]checkin
NSS [HUBUCTF 2022 新生赛]checkin 判断条件是if ($data_unserialize[username]$username&&$data_unserialize[password]$password),满足则给我们flag。正常思路来说,我们要使序列化传入的username和password等于代码中的两个同名变量࿰…...

免费小程序HTTPS证书
随着互联网的快速发展,小程序已经成为人们日常生活中不可或缺的一部分。然而,在小程序的开发和使用过程中,安全问题一直是开发者们关注的重点。其中,HTTPS 证书是保障小程序安全的重要工具之一。在这方面,免费的小程序…...

Linux arm64异常简介和系统调用过程
文章目录 一、异常简介1.1 Exception levels1.2 异常类型 二、系统调用简介2.1 SVC指令2.2 VBAR2.3 系统调用保存现场2.4 系统调用返回 三、Linux 内核分析参考资料 一、异常简介 在ARM64体系架构中,异常是处理器在执行指令时可能遇到的不寻常情况或事件。这些异常…...

我遇到的最蠢的bug,竟然是因为这个原因……
bug的背景 我是一个Python开发者,我最近在做一个数据分析的项目,需要用到pandas库,来处理和分析一些表格数据我的功能需求是,根据用户输入的一些条件,从一个大的数据表中筛选出符合条件的数据,并生成一个新…...
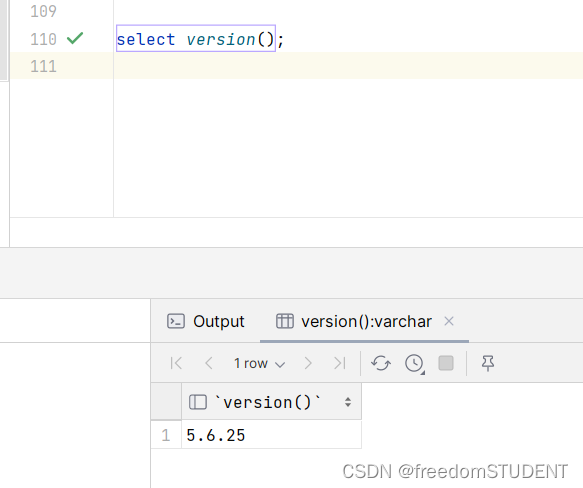
【Mysql】查询mysql的版本
目录 cmd命令查询 mysql -- help(命令) mysql -u root -p(命令) 数据库管理工具查询 select version(); cmd命令查询 mysql -- help(命令) mysql -u root -p(命令) 执行该命令并且输入数据库密码 数据库管理工具查询 selec…...
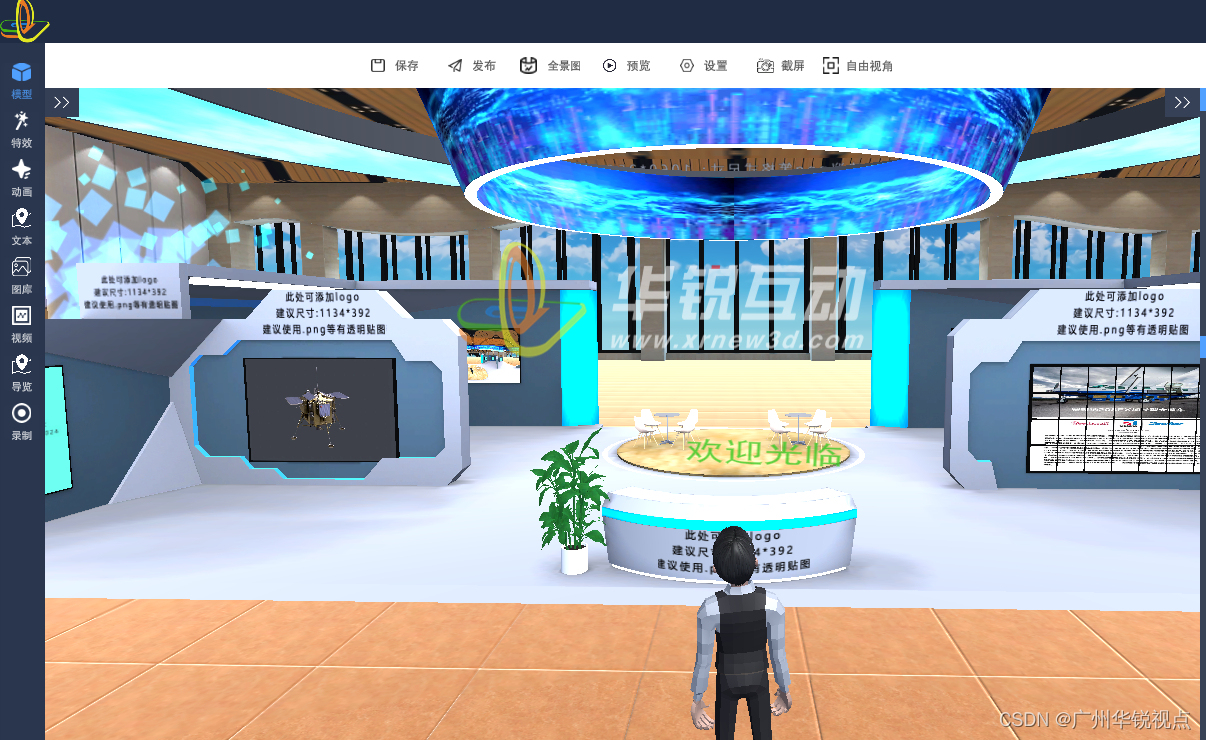
广州华锐互动:VR互动实训内容编辑器助力教育创新升级
随着科技的飞速发展,教育领域也正在经历一场深刻的变革。其中,虚拟现实(VR)技术为教学活动提供了前所未有的便利和可能性。在诸多的VR应用中,VR互动实训内容编辑器无疑是最具潜力和创新性的一种。广州华锐互动开发的这款编辑器以其独特的功能…...
2023最新版本 从零基础入门C++与QT(学习笔记) -1- C++输入与输出
🎏说在前面 🎈我预计是使用两个月的时间玩转C与QT 🎈所以这是一篇学习笔记 🎈根据学习的效率可能提前完成学习,加油!!! 输入(代码如下方代码块) 🎄分析一下构成 🎈…...

Linux:权限篇 (彻底理清权限逻辑!)
shell命令以及运行原理: Linux严格意义上说的是一个操作系统,我们称之为“核心(kernel)“ ,但我们一般用户,不能直接使用kernel。而是通过kernel的“外壳”程序,也就是所谓的shell,来…...

classification_report分类报告的含义
classification_report分类报告 基础知识混淆矩阵(Confusion Matrix)TP、TN、FP、FN精度(Precision)准确率(Accuracy)召回率(Recall)F1分数(F1-score) classi…...
)
mysql with 的用法 (含 with recursive)
mysql with 的用法 (含 with recursive) 相关基础 AS 用法 as 在 mysql 中用来给列/表起别名 如: -- 给列起别名, 把列为name的别名命名为student_name select name as student_name from student; -- 给表起别名, 把表student的别名命名为data_list select * from student…...

YOLOv8模型ONNX格式INT8量化轻松搞定
ONNX格式模型量化 深度学习模型量化支持深度学习模型部署框架支持的一种轻量化模型与加速模型推理的一种常用手段,ONNXRUNTIME支持模型的简化、量化等脚本操作,简单易学,非常实用。 ONNX 模型量化常见的量化方法有三种:动态量化…...

揭秘南卡开放式耳机创新黑科技,核心技术剑指用户痛点
随着科技的进步和人们娱乐方式的升级,大家对听音工具的选择,从传统的耳机到蓝牙耳机再到AirPods这样的真无线耳机,而今年,也有一种全新的耳机爆发式涌入人们之中,那就是开放式耳机。 开放式耳机的出现,满足…...
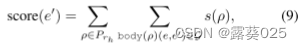
ChatRule:基于知识图推理的大语言模型逻辑规则挖掘11.10
ChatRule:基于知识图推理的大语言模型逻辑规则挖掘 摘要引言相关工作初始化和问题定义方法实验 摘要 逻辑规则对于揭示关系之间的逻辑联系至关重要,这可以提高推理性能并在知识图谱(KG)上提供可解释的结果。虽然已经有许多努力&a…...
6.4翻转二叉树(LC226—送分题,前序遍历)
算法: 第一想法是用昨天的层序遍历,把每一层level用切片反转。但是这样时间复杂度很高。 其实只要在遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。 这道题目使用前序遍历和后序遍历都可以,唯独中序遍历不方便&#x…...

【斗罗二】霍雨浩拿下满分碾压戴华斌,动用家族力量,海神阁会议
Hello,小伙伴们,我是小郑继续为大家深度解析国漫资讯。 深度爆料《绝世唐门》第23话最新预告分析,魂兽升学考试中一场白虎魂师戴华斌与千年级别的风虎的决斗即将上演。风虎,作为虎类魂兽的王者,其强大的实力和独特的技能让这场战…...
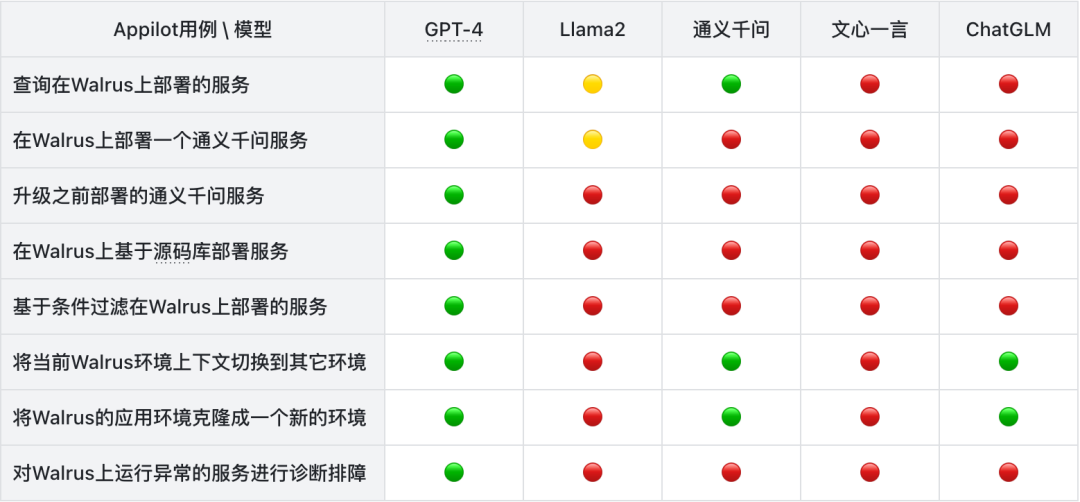
通义千问, 文心一言, ChatGLM, GPT-4, Llama2, DevOps 能力评测
引言 “克隆 dev 环境到 test 环境,等所有服务运行正常之后,把访问地址告诉我”,“检查所有项目,告诉我有哪些服务不正常,给出异常原因和修复建议”,在过去的工程师生涯中,也曾幻想过能够通过这…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
