欧拉角(横滚角、俯仰角、偏航角)、旋转矩阵、四元数的转换与解决万向节死锁
1、概述
物体的位姿(位置和方向)的描述方法一般使用两个坐标系来表示,一个是世界坐标系或地面坐标系,这里我都叫做地面坐标系吧,属于参考坐标系;另一个是自身的坐标系,以飞机为例来讲述一些常见的用语,感觉比较合适,这里就叫做机体坐标系,这个会随着自身的变化而发生变化。
如下图所示:
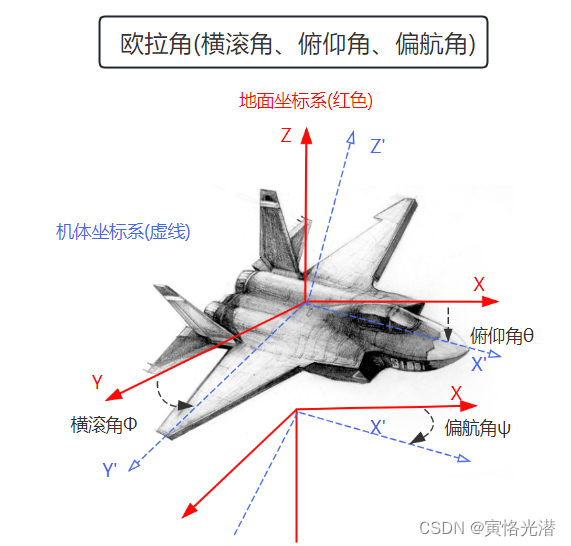
2、机体坐标系
机体坐标系是指固定在飞行器或者飞机上的遵循右手法则的三维正交直角坐标系,其原点位于飞行器的质心。
X'轴永远指向机头,Y'轴指向机身右方,跟X'轴所在的对称平面垂直,Z'轴跟X'轴的所在水平平面垂直。也就是说这个坐标的固定是相对飞机来说的不变化,而上面的地面坐标系是整个的参考坐标,保持固定不变。
3、欧拉角
Euler欧拉角(姿态角):
机体坐标系与地面坐标系的关系是三个角,反应了飞机相对地面的姿态。
横滚角Φ(roll):绕X轴旋转。横滚角是指运载体横轴与水平线之间的夹角。也叫滚转角,代表运载体绕纵轴的转动,绕纵轴轴向顺时针转动为正,否则为负,可以想象成飞机做翻滚运动。
俯仰角θ(pitch):绕Y轴旋转。机体坐标系x轴与水平面的夹角,俯仰角在水平面上面为正,否则为负,可以想象成飞机抬头向上与俯冲向下。
偏航角ψ(yaw):绕Z轴旋转。相对于纵轴的旋转角度,改变偏航角可以改变飞机的飞行方向,机头往右为正,这个跟平时开车,左转弯右转弯一样。
4、欧拉角转换旋转矩阵
当然这个欧拉角的旋转顺序也是很有关系的,都是描述着一个坐标系到另一个坐标系的变化,也就是说一个坐标系相对于另一个坐标系的位姿可以使用一个旋转矩阵来表示。其旋转矩阵我们来看下推导如下:

5、四元数
四元数,又称欧拉参数,提供另外一种方法来表述三维旋转。四元数方法用在大多数的演算会比较快捷,并能避免一些技术上的问题,如万向节死锁(即当旋转角度接近某些特定值时,欧拉角表示会出现无限循环,换句话说就是两个轴重合,失去一个自由度,然后再旋转也没啥意义了) 现象,因为这些原因,许多高速度三维图形程式制作都使用四元数。当然四元数没有欧拉角来的直观,比较难以理解,这个也是它的缺点。
欧拉角和四元数都是用于描述旋转和方向的方法,但它们在表示旋转的方式和数学结构上有所不同。
对于万向节死锁的情况,可以查看视频来更直观了解:欧拉旋转万向节死锁
四元数是四个自由度,比欧拉角多出一个自由度:
Q=a+bi+cj+dk,其中a,b,c,d是实数,i,j,k是虚数,i²=j²=k²=-1
6、Python示例
6.1、欧拉角转旋转矩阵
import math
import numpy as np
def euler_to_matrix(theta) :R_x = np.array([[1, 0,0],[0,math.cos(theta[0]), -math.sin(theta[0])],[0,math.sin(theta[0]), math.cos(theta[0])]]) R_y = np.array([[math.cos(theta[1]), 0,math.sin(theta[1])],[0,1,0],[-math.sin(theta[1]),0,math.cos(theta[1])]])R_z = np.array([[math.cos(theta[2]), -math.sin(theta[2]),0],[math.sin(theta[2]), math.cos(theta[2]),0],[0,0,1]]) R = np.dot(R_z, np.dot( R_y, R_x ))return R分别计算绕x、y、z轴的旋转矩阵,然后以某个顺序做点积运算即可。
print(euler_to_matrix([math.pi/3,0,math.pi/6]))
/*
[[ 0.8660254 -0.25 0.4330127][ 0.5 0.4330127 -0.75 ][-0. 0.8660254 0.5 ]]
*/使用transforms3d或者scipy里面的库,分别来验证下,答案是正确的:
import transforms3d as tfs
print(tfs.euler.euler2mat(math.pi/3,0,math.pi/6,"sxyz"))
print(np.degrees(tfs.euler.mat2euler(euler_to_matrix([math.pi/3,0,math.pi/6]),"sxyz"))) #[60. -0. 30.]//使用弧度制
from scipy.spatial.transform import Rotation as R
print(R.from_euler('xyz', [math.pi/3,0,math.pi/6], degrees=False).as_matrix())
print(np.degrees(R.from_matrix(euler_to_matrix([math.pi/3,0,math.pi/6])).as_euler('xyz'))) #[60. 0. 30.]
//使用角度制
print(R.from_euler('xyz', [60,0,30], degrees=True).as_matrix())一般我们都是以弧度为标准,当然有些情况为了直观,我们也可以转成角度来运算。
6.2、欧拉角转四元数
import mathdef euler_to_quaternion(roll, pitch, yaw):cy = math.cos(yaw * 0.5)sy = math.sin(yaw * 0.5)cr = math.cos(roll * 0.5)sr = math.sin(roll * 0.5)cp = math.cos(pitch * 0.5)sp = math.sin(pitch * 0.5)w = cy * cr * cp + sy * sr * spx = cy * sr * cp - sy * cr * spy = cy * cr * sp + sy * sr * cpz = sy * cr * cp - cy * sr * spreturn w, x, y, zprint(euler_to_quaternion(math.pi/3,0,math.pi/6))
#(0.8365163037378079, 0.4829629131445341, 0.12940952255126034, 0.2241438680420134)print(tfs.euler.euler2quat(math.pi/3,0,math.pi/6,"sxyz"))
#[0.8365163 0.48296291 0.12940952 0.22414387]print(euler_to_quaternion(math.pi/3,math.pi,math.pi/2))
#(0.3535533905932738, -0.6123724356957946, 0.6123724356957946, -0.3535533905932737)print(tfs.euler.euler2quat(math.pi/3,math.pi,math.pi/2,"sxyz"))
#array([ 0.35355339, -0.61237244, 0.61237244, -0.35355339])6.3、四元数转旋转矩阵
#x, y ,z ,w
def quaternion_to_rotation_matrix(q):rot_matrix = np.array([[1.0 - 2 * (q[1] * q[1] + q[2] * q[2]), 2 * (q[0] * q[1] - q[3] * q[2]), 2 * (q[3] * q[1] + q[0] * q[2])],[2 * (q[0] * q[1] + q[3] * q[2]), 1.0 - 2 * (q[0] * q[0] + q[2] * q[2]), 2 * (q[1] * q[2] - q[3] * q[0])],[2 * (q[0] * q[2] - q[3] * q[1]), 2 * (q[1] * q[2] + q[3] * q[0]), 1.0 - 2 * (q[0] * q[0] + q[1] * q[1])]],dtype=q.dtype)return rot_matrixr_matrix=quaternion_to_rotation_matrix(np.array([0.4829629,0.12940952,0.22414387,0.8365163]))
print(r_matrix)
/*
[[ 8.66025403e-01 -2.50000007e-01 4.33012693e-01][ 4.99999996e-01 4.33012726e-01 -7.49999975e-01][ 1.23449401e-09 8.66025378e-01 5.00000027e-01]]
*/6.4、旋转矩阵转欧拉角
def rotation_matrix_to_euler(R) :sy = math.sqrt(R[0,0] * R[0,0] + R[1,0] * R[1,0])singular = sy < 1e-6if not singular :x = math.atan2(R[2,1] , R[2,2])y = math.atan2(-R[2,0], sy)z = math.atan2(R[1,0], R[0,0])else :x = math.atan2(-R[1,2], R[1,1])y = math.atan2(-R[2,0], sy)z = 0return np.array([x, y, z])print(rotation_matrix_to_euler(r_matrix))
//弧度
#[ 1.04719751e+00 -1.23449401e-09 5.23598772e-01]
print(np.degrees(rotation_matrix_to_euler(r_matrix)))
//角度
#[ 5.99999979e+01 -7.07312966e-08 2.99999998e+01]7、小结
这里通过画图直观了解到两种坐标系的关系,以及飞机在飞行过程中产生的欧拉角的多种表示方法,由于欧拉角是三自由度,当两根轴重叠之后将发生“万向节死锁”的问题,所以我们一般都使用四元数来代替欧拉角,四个自由度避免了万向节发生死锁。
由于不同顺序的旋转将会产生不一样的旋转矩阵,这里我也通过三角函数的知识,将欧拉角分别沿着三个轴做旋转得到的旋转矩阵做了推导,希望可以帮助到大家更好地理解。
相关文章:

欧拉角(横滚角、俯仰角、偏航角)、旋转矩阵、四元数的转换与解决万向节死锁
1、概述 物体的位姿(位置和方向)的描述方法一般使用两个坐标系来表示,一个是世界坐标系或地面坐标系,这里我都叫做地面坐标系吧,属于参考坐标系;另一个是自身的坐标系,以飞机为例来讲述一些常见…...

Java Post请求参数格式为XML
方式一: public static void PostXml1(String url, String xml) throws IOException {OkHttpClient client new OkHttpClient().newBuilder().build();//okhttp3.MediaType mediaType okhttp3.MediaType.parse("application/xml");okhttp3.MediaType m…...
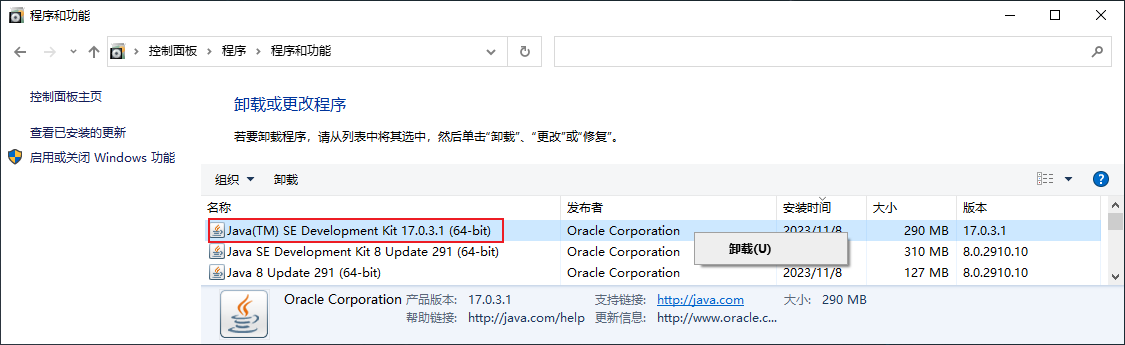
Windows 安装 JDK 8 和 JDK 17 和多版本JDK切换
目录 下载 JDK安装 JDK配置环境变量卸载 JDK卸载 JDK 8卸载 JDK 17 下载 JDK JDK 8 下载地址:https://www.aliyundrive.com/s/koYe1SVRg76 JDK 17 下载地址: https://www.aliyundrive.com/s/tBcbUtAHTbg 安装 JDK 点击可执行文件 jdk-8u291-windows-…...
SpringData、SparkStreaming和Flink集成Elasticsearch
本文代码链接:https://download.csdn.net/download/shangjg03/88522188 1 Spring Data框架集成 1.1 Spring Data框架介绍 Spring Data是一个用于简化数据库、非关系型数据库、索引库访问,并支持云服务的开源框架。其主要目标是使得对数据的访问变得方便快…...

中国电子学会2023年09月份青少年软件编程Python等级考试试卷六级真题(含答案)
2023-09 Python六级真题 分数:100 题数:38 测试时长:60min 一、单选题(共25题,共50分) 1. 以下选项中,不是tkinter变量类型的是?(D )(2分) A.IntVar() B.StringVar() C.Do…...
)
基于STM32设计的智能水母投喂器(华为云IOT)
基于STM32设计的智能水母养殖系统 一、设计简述 1.1 项目背景 水母是一种非常美丽和神秘的生物,在许多人的眼中,它不仅是一种宽广的海洋世界中的一道美丽的风景线,同时也是一种珍贵的实验动物和养殖资源。随着水母的养殖需求不断增多,一个高效、智能、可控的水母养殖系统…...
合成数据加速机器视觉学习
虽然机器学习在基于视觉的自动化中的应用正在增长,但许多行业都面临着挑战,并难以在其计算机视觉应用中实施它。这在很大程度上是由于需要收集许多图像,以及与准确注释这些图像中的不同产品相关的挑战。 该领域的最新趋势之一是利用合成数据…...
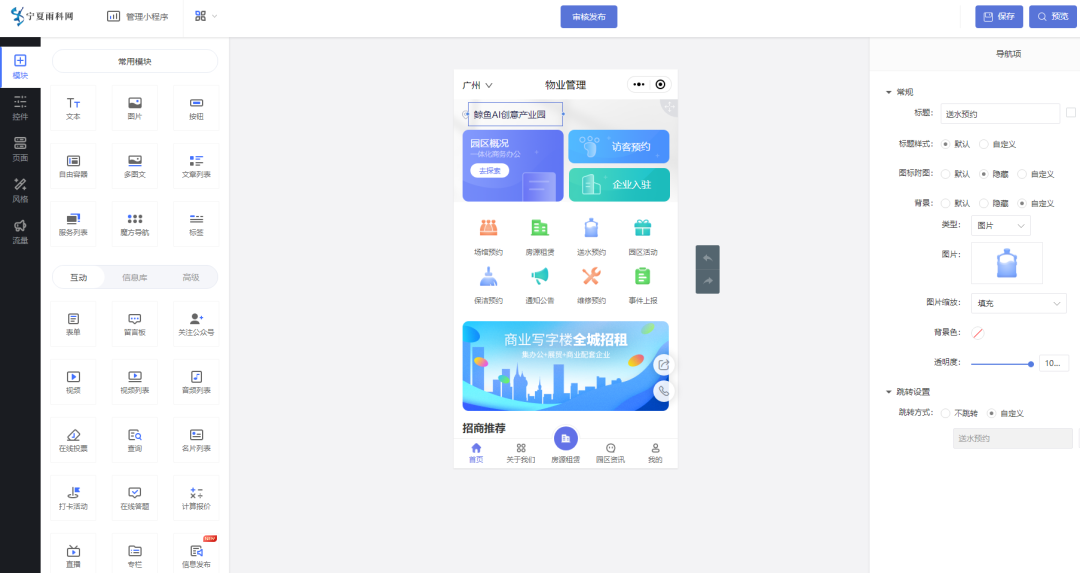
物业管理服务预约小程序的效果如何
物业所涵盖的场景比较多,如小区住宅、办公楼、医院、度假区等,而所涵盖的业务也非常广,而在实际管理中,无论对外还是对内也存在一定难题: 1、品牌展示难、内部管理难 物业需求度比较广,设置跨区域也可以&…...

ORA-00257: Archiver error. Connect AS SYSDBA only until resolved错误解决
错误的原因:是因为服务器分配空间不足,数据库归档日志满导致系统数据库登陆失败。 解决办法:1.删除以前的日志 2.增大归档日志的容量 3.关闭归档模式 一、删除以前的容量 1.登录账号后,查看ORACLE_BASE目录 【oraclelocalhost~】$…...
)
backbone:从AlexNet到...(持续补充ing)
文章目录 Introduction(前言知识)代码参考卷积、池化输出退化1*1卷积减少或增加通道数自然的减少计算量解决了什么问题,达到了什么样的效果AlexNet整体结构如下VGGNet网络结构如下,D、E分别代表VGG-16、VGG-19下图为VGG-16ResNet结构如下DenseNet结构如下Dense Block——特…...

FiRa标准——MAC实现(二)
在IEEE 802.15.4z标准中,最关键的就是引入了STS(加扰时间戳序列),实现了安全测距,大大提高了测距应用的安全性能。在FiRa的实现中,其密钥派生功能是非常重要的一个部分,本文首先对FiRa MAC中加密…...

oracle中分组函数LISTAGG
前言 Oracle中的 GROUP_CONCAT 函数用于将多行数据合并为一行,并以指定的分隔符分隔各个值。在Oracle中,没有直接的GROUP_CONCAT函数,但可以使用 LISTAGG 函数来实现类似的功能。 如何使用 1、使用SELECT语句选择需要合并的列,…...
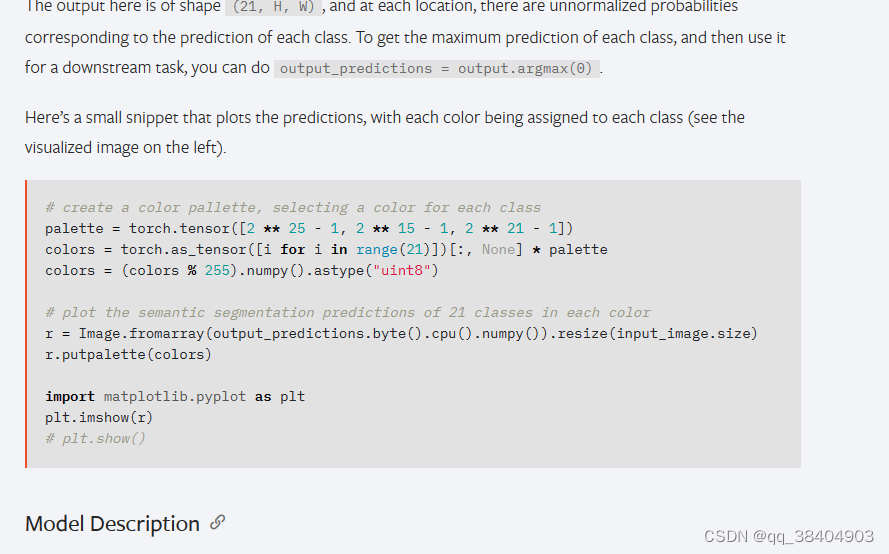
深度学习pytorch之hub模块
pytorchhub模块里面有很多模型 https://pytorch.org/hub/ github网址:https://github.com/pytorch/pytorch import torch model torch.hub.load(pytorch/vision:v0.10.0, fcn_resnet50, pretrainedTrue) # or # model torch.hub.load(pytorch/vision:v0.10.0, fc…...
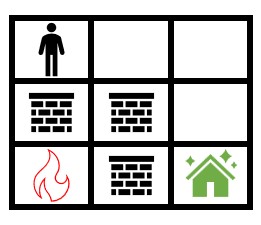
LeetCode 2258. 逃离火灾:BFS
【LetMeFly】2258.逃离火灾 力扣题目链接:https://leetcode.cn/problems/escape-the-spreading-fire/ 给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ,它表示一个网格图。每个格子为下面 3 个值之一: 0 表示草地。1 表示着火的格…...
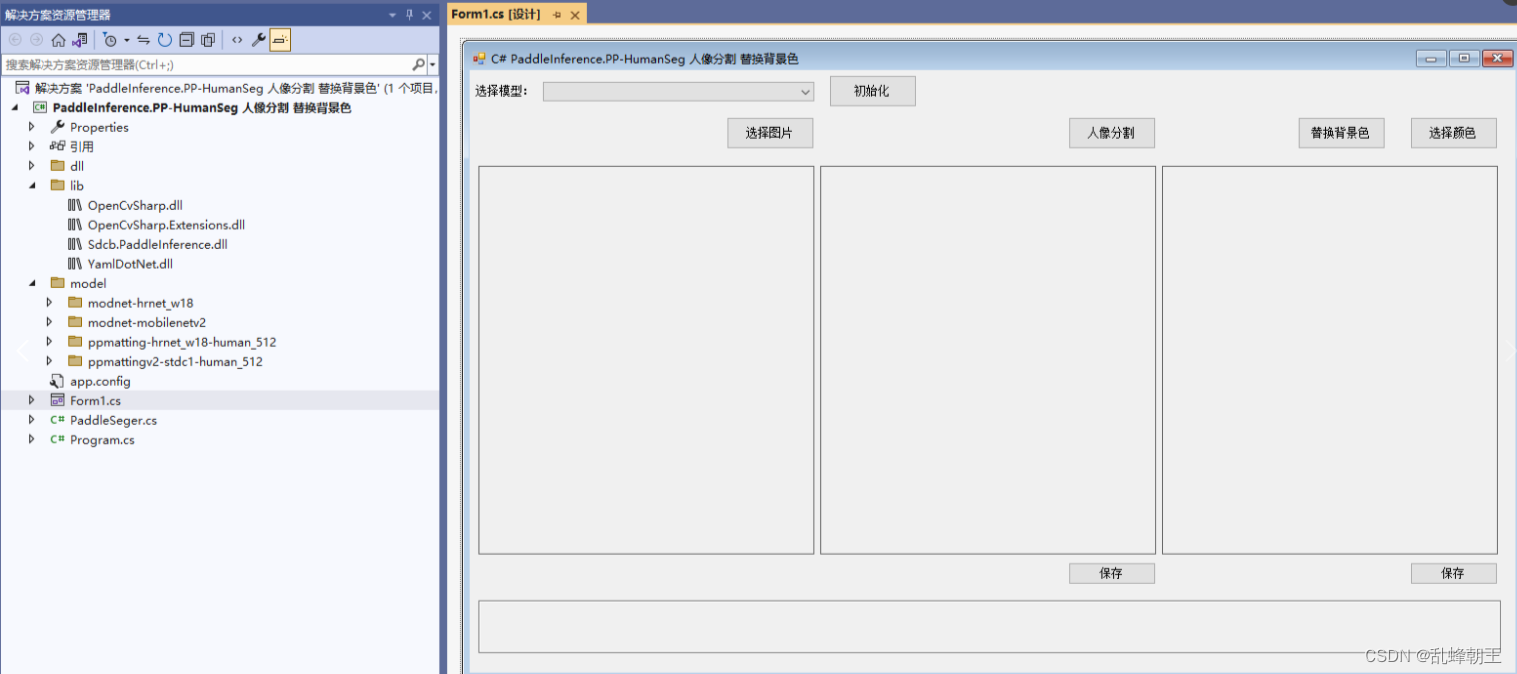
C# PaddleInference.PP-HumanSeg 人像分割 替换背景色
效果 项目 VS2022.net4.8OpenCvSharp4Sdcb.PaddleInference 包含4个分割模型 modnet-hrnet_w18 modnet-mobilenetv2 ppmatting-hrnet_w18-human_512 ppmattingv2-stdc1-human_512 代码 using OpenCvSharp; using Sdcb.PaddleInference; using System; using System.Col…...

Java 变量初始化的两种方式和优缺点比较
第一种初始化方式:(优先推荐) String fileRename null; File fileToSave null; 这种方式将变量的作用域限定在循环外部,即在整个代码块中都可以使用这些变量。初始值为null表示变量在开始时没有具体的数值。 这种方式更好的…...

15.三数之和
题目来源: leetcode题目,网址:15. 三数之和 - 力扣(LeetCode) 解题思路: 1.三重循环暴力遍历,超时原因,三重循环复杂度太高 2.双重循环哈希表,超时原因,哈…...

竞赛选题 深度学习疲劳驾驶检测 opencv python
文章目录 0 前言1 课题背景2 实现目标3 当前市面上疲劳驾驶检测的方法4 相关数据集5 基于头部姿态的驾驶疲劳检测5.1 如何确定疲劳状态5.2 算法步骤5.3 打瞌睡判断 6 基于CNN与SVM的疲劳检测方法6.1 网络结构6.2 疲劳图像分类训练6.3 训练结果 7 最后 0 前言 🔥 优…...
PROFINET和UDP、MODBUS-RTU通信速度对比实验
这篇博客我们介绍PROFINET 和MODBUS-RTU通信实验时的数据刷新速度,以及这种速度不同对控制系统带来的挑战都有哪些,在介绍这篇对比实验之前大家可以参考下面的文章链接: S7-1200PLC和SMART PLC的PN智能从站通信 S7-200 SMART 和 S7-1200PLC进行PROFINET IO通信-CSDN博客文…...
CSS3 多媒体查询、网格布局
一、CSS3多媒体查询: CSS3 多媒体查询继承了CSS2多媒体类型的所有思想,取代了查找设备的类型。CSS3根据设置自适应显示。 多媒体查询语法: media not|only mediatype and (expressions) { CSS 代码...; } not: not是用来排除掉某些特定…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

uniapp获取当前位置和经纬度信息
1.1. 获取当前位置和经纬度信息(需要配置高的SDK) 调用uni-app官方API中的uni.chooseLocation(),即打开地图选择位置。 <button click"getAddress">获取定位</button> const getAddress () > {uni.chooseLocatio…...

若依项目部署--传统架构--未完待续
若依项目介绍 项目源码获取 #Git工具下载 dnf -y install git #若依项目获取 git clone https://gitee.com/y_project/RuoYi-Vue.git项目背景 随着企业信息化需求的增加,传统开发模式存在效率低,重复劳动多等问题。若依项目通过整合主流技术框架&…...
