ARC142D Deterministic Placing
ARC142D Deterministic Placing
题目大意
有一棵nnn个顶点的树,每个点上最多放一张卡片,你可以做如下操作:
- 同时将所有的卡片移到它所在顶点的相邻的一个顶点上
一个操作我们说它是好的,当下列条件满足:
- 每条边最多被某张卡片经过
- 每个顶点最多被一张卡片占据
小TTT可以选择一个或多个顶点来放置卡片,一个顶点放置一张卡片。他有2n−12^n-12n−1种方式,求满足以下条件的方案数:
对于每个非负整数kkk
- 它能连续进行kkk次好的操作
- 令SkS_kSk表示经过刚好kkk次操作后被卡片占据的点的集合,则SkS_kSk是唯一的
题解
第一步:分树为链
我们可以发现,每一张卡片都是在两个点上反复横跳的。我们把每个反复横跳的边拿出来,那一定是若干条不相交的链。且这些链一定是以空点为顶部,有卡片的点为中部和尾部(一条链不能只有一个空点)。这些链一定能填满整棵树。
假设x,yx,yx,y为相邻的两个点且在不同的链上,为了避免重复和不合法的情况,我们做一些规定。
- 如果xxx链的端点且yyy为链的中间点,则在第二次操作时,在yyy上的卡片可以向xxx移动,则SkS_kSk不唯一
- 如果x,yx,yx,y都是链的顶部,则第一次操作后两条链合并成一条链,可以往两个方向移动,SkS_kSk不唯一
- 如果x,yx,yx,y都是链的尾部,则第一次操作时xxx的位置空出了,yyy所在可以往链头或xxx移动,SkS_kSk不唯一
其余情况都是合法的。
第二步:树形DP
定义fu,if_{u,i}fu,i表示点uuu第iii种状态下的方案数。各种状态如下:
- fu,0f_{u,0}fu,0表示uuu为链身,且uuu在链上无前无后
- fu,1f_{u,1}fu,1表示uuu为链身,且uuu在链上有前无后
- fu,2f_{u,2}fu,2表示uuu为链身,且uuu在链上无前有后
- fu,3f_{u,3}fu,3表示uuu为链身,且uuu在链上有前有后
- fu,4f_{u,4}fu,4表示uuu为链头,且uuu在链上无后面的点
- fu,5f_{u,5}fu,5表示uuu为链头,且uuu在链上有后面的点
- fu,6f_{u,6}fu,6表示uuu为链尾,且uuu在链上无后面的点
- fu,7f_{u,7}fu,7表示uuu为链尾,且uuu在链上有后面的点
有前或有前面的点即存在链头,有后或有后面的点即存在链尾。
为了防止在转移的时候计算重复,我们还需要定义gu,ig_{u,i}gu,i。假设当前枚举的是uuu的各个儿子,且枚举到的儿子为vvv,则fu,if_{u,i}fu,i表示点uuu在统计vvv之前的各种状态的方案数,ggg表示统计vvv之后的方案数,则可以用fu,if_{u,i}fu,i和fv,if_{v,i}fv,i来更新ggg,在vvv的贡献计算完之后再将ggg的值赋值给fff,然后计算uuu的下一个儿子。
因为状态比较多,所以转移式也比较多。除去不合法的情况,有202020种转移方法,具体见代码。
对于每个点,状态0,4,60,4,60,4,6的fff的初值为111。最后的答案为f1,3+f1,5+f1,7f_{1,3}+f_{1,5}+f_{1,7}f1,3+f1,5+f1,7。
总结
这道题主要是用树形DP,考虑各种状态来进行状态转移。时间复杂度为O(n)O(n)O(n)。
注:代码中gt(v1,v2,v3)gt(v1,v2,v3)gt(v1,v2,v3)表示gu,v1=fu,v2×fv,v3g_{u,v1}=f_{u,v2}\times f_{v,v3}gu,v1=fu,v2×fv,v3,vvv为uuu的儿子。这一步即用uuu点的状态v2v2v2的fff和vvv点的状态v2v2v2的fff值更新ggg的状态v1v1v1。
code
#include<bits/stdc++.h>
using namespace std;
int n,x,y,tot=0,d[500005],l[500005],r[500005];
long long v[10],f[200005][8];
long long mod=998244353;
void add(int xx,int yy){l[++tot]=r[xx];d[tot]=yy;r[xx]=tot;
}
void pt(int v1,int v2,int v3){v[v1]=(v[v1]+f[x][v2]*f[y][v3]%mod)%mod;
}
void dfs(int u,int fa){f[u][0]=f[u][4]=f[u][6]=1;for (int i=r[u];i;i=l[i]){if(d[i]==fa) continue;dfs(d[i],u);for (int j=0;j<8;j++) v[j]=0;x=u;y=d[i];pt(0,0,3);pt(1,0,4);pt(1,0,1);pt(1,1,3);pt(2,0,6);pt(2,0,2);pt(2,2,3);pt(3,2,4);pt(3,1,6);pt(3,1,2);pt(3,2,1);pt(3,3,3);pt(4,4,7);pt(5,5,7);pt(5,4,2);pt(5,4,6);pt(6,6,5);pt(7,7,5);pt(7,6,1);pt(7,6,4);for(int j=0;j<8;j++) f[u][j]=v[j];}
}
int main()
{scanf("%d",&n);for(int i=1;i<n;i++){scanf("%d%d",&x,&y);add(x,y);add(y,x);}dfs(1,0);printf("%lld",(f[1][3]+f[1][5]+f[1][7])%mod);return 0;
}
相关文章:

ARC142D Deterministic Placing
ARC142D Deterministic Placing 题目大意 有一棵nnn个顶点的树,每个点上最多放一张卡片,你可以做如下操作: 同时将所有的卡片移到它所在顶点的相邻的一个顶点上 一个操作我们说它是好的,当下列条件满足: 每条边最…...

阶段八:服务框架高级(第二章:分布式事务)
阶段八:服务框架高级(第二章:分布式事务)Day-分布式事务0.学习目标1.分布式事务问题1.1.本地事务1.2.分布式事务1.3.演示分布式事务问题2.理论基础2.1.CAP定理2.1.1.一致性2.1.2.可用性2.1.3.分区容错2.1.4.矛盾2.2.BASE理论2.3.解…...
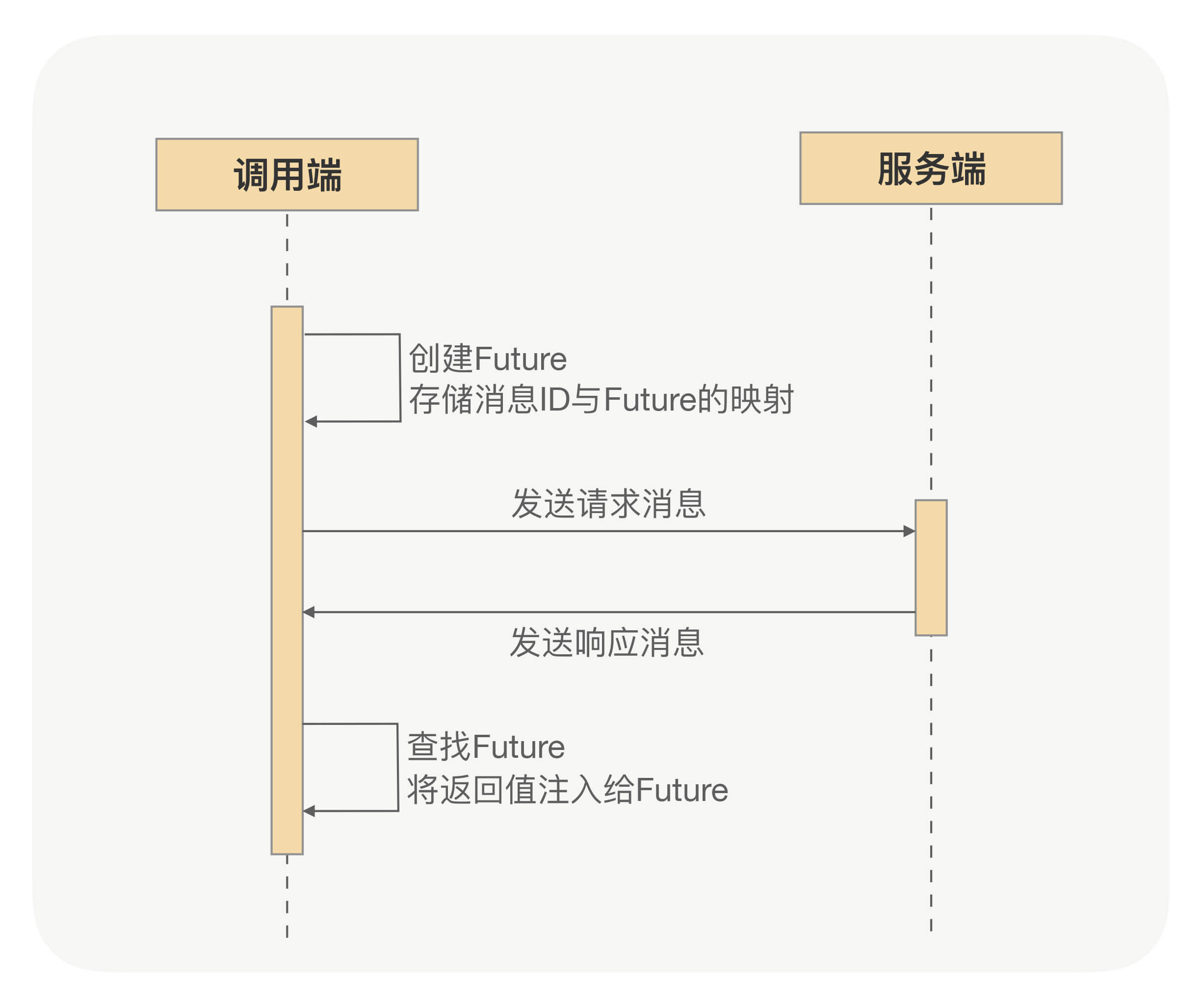
RPC异步化原理
深入RPC,更好使用RPC,须从RPC框架整体性能考虑问题。得知道如何提升RPC框架的性能、稳定性、安全性、吞吐量及如何在分布式下快速定位问题。RPC框架如何压榨单机吞吐量? 1 前言 TPS一直上不去,压测时CPU压到40%~50%就…...

C# 多窗口切换的实现
1、目的在主窗口中根据不同的按钮选择不同的子窗口显示。2、实现(1)、创建Winform窗体程序,放入SplitContainer控件splitContainer1将窗体分成左右2部分;(2)、在左侧splitContainer1.panel1中放入3个Button…...
【深度学习】RNN
1. 什么是RNN 循环神经网络(Recurrent Neural Network, RNN)是一类以序列(sequence)数据为输入,在序列的演进方向进行递归(recursion)且所有节点(循环单元)按链式连接的递…...

招聘岗位,机会难得
岗位需求 费话不多说,直接上JD: 嵌入式开发工程师: 17:411.计算机、通信等相关专业。 2.熟悉网络基础知识,熟悉802.11a/b/g/n/ac协议,能通过抓包等分析手段排查定位各种wifi相关问题。 3.熟悉路由器主要功能及实现原…...
)
web打印的几种方法(2023)
在工作中出现web打印的情况是非常多的,其实这也是一个比较烦人的问题,这篇博客整理一下关于Web打印的一些方法或者方式。 1. window.print() 这个方法是用来打印网页的,页面上的其他的元素也会被打印处理,在打印的时候页眉页脚是…...
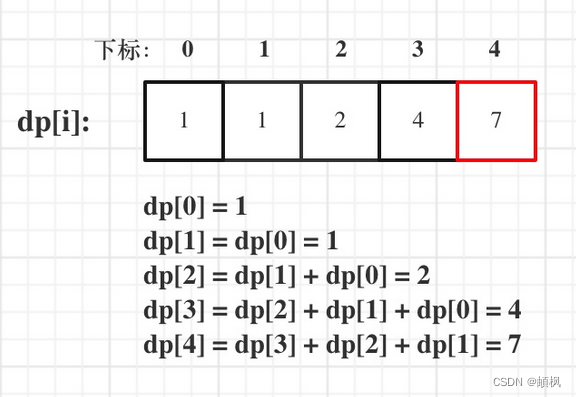
代码随想录算法训练营day44 | 动态规划之完全背包 518. 零钱兑换 II 377. 组合总和 Ⅳ
day44完全背包基础知识问题描述举个栗子518. 零钱兑换 II1.确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组377. 组合总和 Ⅳ1.确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例来推导dp数组完全背包基…...
IntelliJ IDEA 实用插件推荐(包含使用教程)
IntelliJ IDEA 实用插件推荐 背景:电脑重装了,重新下载了最新版的IntelliJ IDEA,感觉默认模式有点枯燥,于是决定从网上下载一些实用美观的插件优化自己以后吃饭的工具,现在推荐的都是目前还能用的(亲身实践…...

WideDeep模型
google提出的Wide&deep模型,将线性模型与DNN很好的结合起来,在提高模型泛化能力的同时,兼顾模型的记忆性。wide&deep这种将线性模型与DNN的并行连接模式,后来称为推荐领域的经典模式,奠定了后面深度学习模型的…...
nacos集群模式+keepalived搭建高可用服务
实际工作中如果nacos这样的核心服务停掉了或者整个服务器宕机了,那整个系统也就gg了,所以像这样的核心服务我们必须要搞个3个或者3个以上的nacos集群部署,实现高可用; 部署高可用版本之前,首先你要会部署单机版的naco…...

吉利「银河」负重突围
吉利控股集团最新公布的数据显示,2022年,吉利控股集团汽车总销量超230万辆,同比增长4.3%。其中,新能源汽车销量超64万辆,同比增长100.3%。 在中国本土市场,2022年吉利集团旗下品牌乘用车总交付量为135.84万…...

QT之图形视图框架概述——Graphics View Framework
QT之图形视图框架概述——Graphics View Framework1. 概述2. 核心类3. 事件传递4. Graphics View 坐标系统5. 参考1. 概述 Graphics View Framework是子Qt 4.2引入的,用来取代之前版本中的QCanvas。Graphics View Framework提拱了用于大量2D图形项的管理和交互的能…...
:数仓报表场景(上) 从分析函数效率一定快吗聊一聊结果集分页和隔行抽样实现方式)
【SQL开发实战技巧】系列(二十二):数仓报表场景(上) 从分析函数效率一定快吗聊一聊结果集分页和隔行抽样实现方式
系列文章目录 【SQL开发实战技巧】系列(一):关于SQL不得不说的那些事 【SQL开发实战技巧】系列(二):简单单表查询 【SQL开发实战技巧】系列(三):SQL排序的那些事 【SQL开发实战技巧…...

小米无线AR眼镜探索版细节汇总
在MWC 2023期间,小米正式发布了一款无线AR眼镜,虽然还没看过实机,但XDA提前上手体验,我们从中进行总结。首先我要说的是,小米这款眼镜和高通无线AR眼镜参考设计高度重叠,产品卖点几乎一致,只是增…...

Web3中文|Litra:简洁而优美的NFT流动性协议,能给NFT市场带来什么?
2021年,NFT元年2021年,无疑是 NFT 的“元年”。这一年推特创始人的首条推特被拍出250万美元,加密艺术家Beeple的数字作品“First 5000 Days”在佳士得以6900万美元价格成交,无聊猿最高上涨了1800倍。2021年11月,在Goog…...

SSL证书对虚拟主机的用处有哪些?
虚拟主机是指在同一台服务器上,通过不同的域名或IP地址为多个网站提供服务的一种网络主机。而SSL证书则是一种数字证书,它用于加密网站与用户之间的通信,确保数据传输的安全性和完整性。在虚拟主机上,SSL证书有以下几个用处&#…...
SpringCloud之MQ笔记分享
MQ异步通信 初始MQ 同步通信 优点:时效性较强,可以以及得到结果 Feign就属于同步方式–问题: 耦合问题性能下降(中间的等待时间)资源浪费级联失败 异步通信 优点 耦合度低性能提升,吞吐量高故障隔离…...
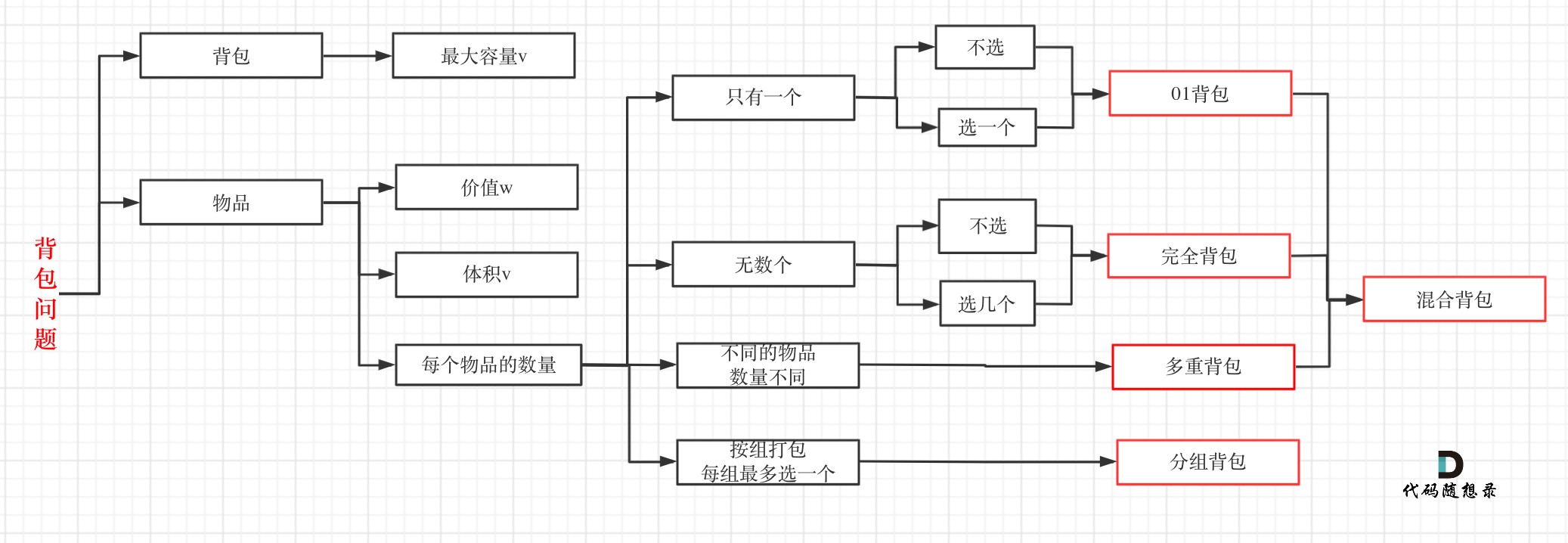
动态规划背包问题
背包问题的分类 拿到背包问题,最重要的是会归类到哪一种背包问题中,常见的考题里主要是01背包和完全背包,leetcode上连多重背包的题目都没有。实际完全背包问题就是01背包的一种。 对一和零这道题,很多人容易把m看成一个背包,n看成另一个背包,从而当做多重背包。然而这…...

OpenCV4.x图像处理实例-张嘴和闭嘴检测
张嘴和闭嘴检测 在活体验证中,张嘴和闭嘴检测也是一个重要的环节。本文将介绍如何通过检测人脸上唇和下唇的关键点,并计算上唇和下唇的关键点的距离来检测当前人脸状态是否处于张嘴或闭嘴。 张嘴和闭嘴检测主要步骤如下: 第一步,安装依赖库 示例中使用到OpenCV和MediaP…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...

Android Framework预装traceroute执行文件到system/bin下
文章目录 Android SDK中寻找traceroute代码内置traceroute到SDK中traceroute参数说明-I 参数(使用 ICMP Echo 请求)-T 参数(使用 TCP SYN 包) 相关文章 Android SDK中寻找traceroute代码 设备使用的是Android 11,在/s…...
