华为ensp:交换机接口划分vlan
 现在要把
现在要把
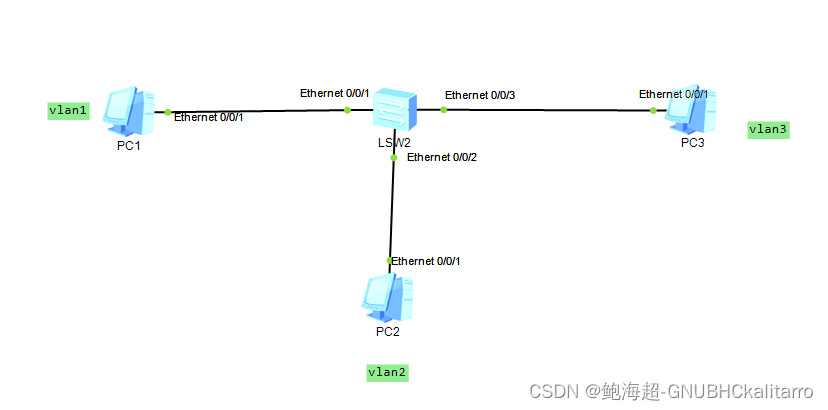
e0/0/1 接口放入vlan1
e0/0/2 接口放入vlan2
e0/0/3 接口放入vlan3
默认所有接口都在vlan1所以 e0/0/0 接口不用动
1.创建vlan
进入系统视图模式
直接输入 vlan 编号 即可创建对应vlan
vlan 编号
vlan 2创建vlan2
vlan 3创建vlan3

2.将接口进入vlan
int e0/0/2进入e0/0/2接口
port link-type access 切换为access模式
port default vlan 2将接口加入vlan2
这样我们的e0/0/2就加入进vlan2了
---------------------------------------------------------------------------------------
e0/0/3接口加入vlan3也是同样操作
interface e0/0/3port link-type access port default vlan 3成功将e0/0/3接口加入vlan3
3.查看结果
display vlan查看vlan划分
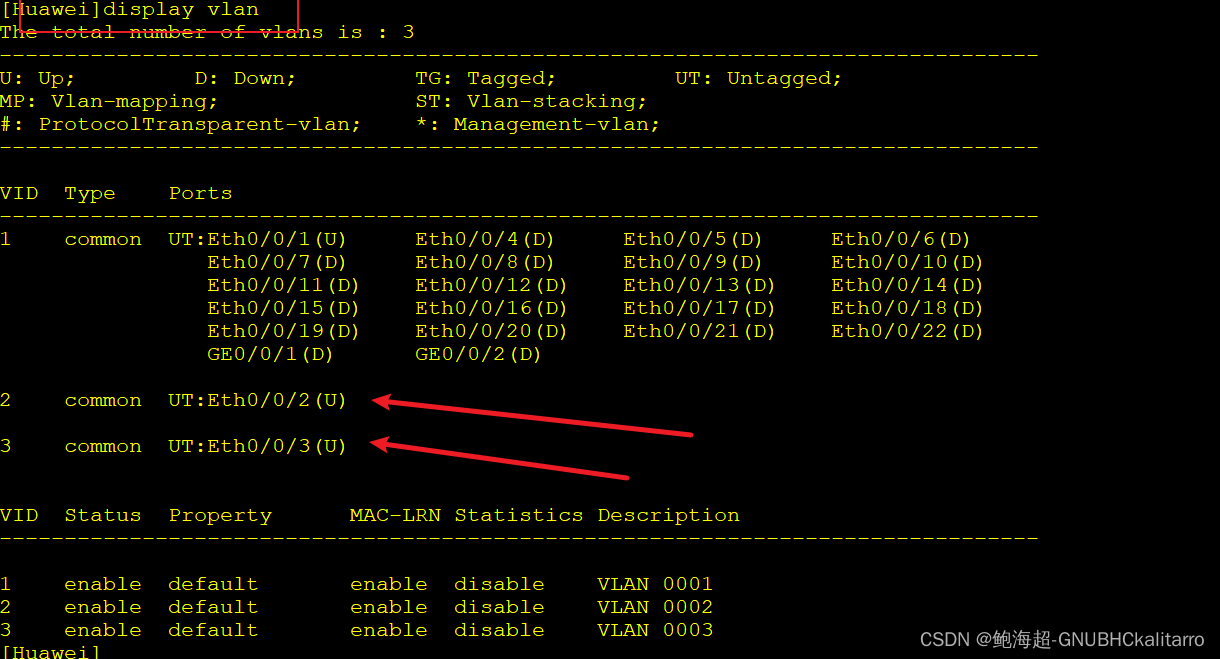
可以看见前面的数字1 , 2 , 3 就是对应的vlan编号,后面的就是vlan内的接口
相关文章:

华为ensp:交换机接口划分vlan
现在要把 e0/0/1 接口放入vlan1 e0/0/2 接口放入vlan2 e0/0/3 接口放入vlan3 默认所有接口都在vlan1所以 e0/0/0 接口不用动 1.创建vlan 进入系统视图模式 直接输入 vlan 编号 即可创建对应vlan vlan 编号 vlan 2 创建vlan2 vlan 3 创建vlan3 2.将接口进入vlan…...
PCBA表面污染的分类及处理方法
NO.1 引言 在PCBA生产过程中,锡膏和助焊剂会产生残留物质,残留物中包含的有机酸和电离子,前者易腐蚀PCBA,后者会造成焊盘间短路故障。且近年来,用户对产品的清洁度要求越来越严格,PCBA清洗工艺逐渐被电子组…...
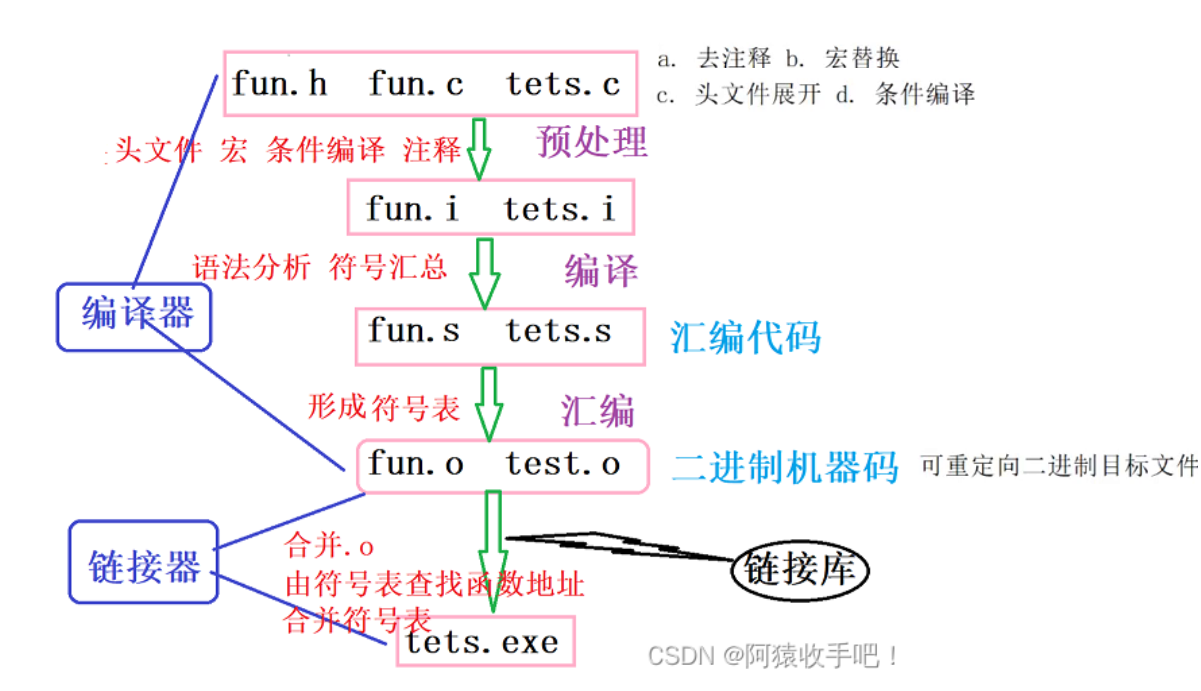
Linux开发工具之编辑器vim
文章目录 1.vim是啥?1.1问问度娘1.2自己总结 2.vim的初步了解2.1进入和退出2.2vim的模式1.介绍2.使用 3.vim的配置3.1自己配置3.2下载插件3.3安装大佬配置好的文件 4.程序的翻译 1.vim是啥? 1.1问问度娘 1.2自己总结 vi/vim都是多模式编辑器,vim是vi的升级版本&a…...
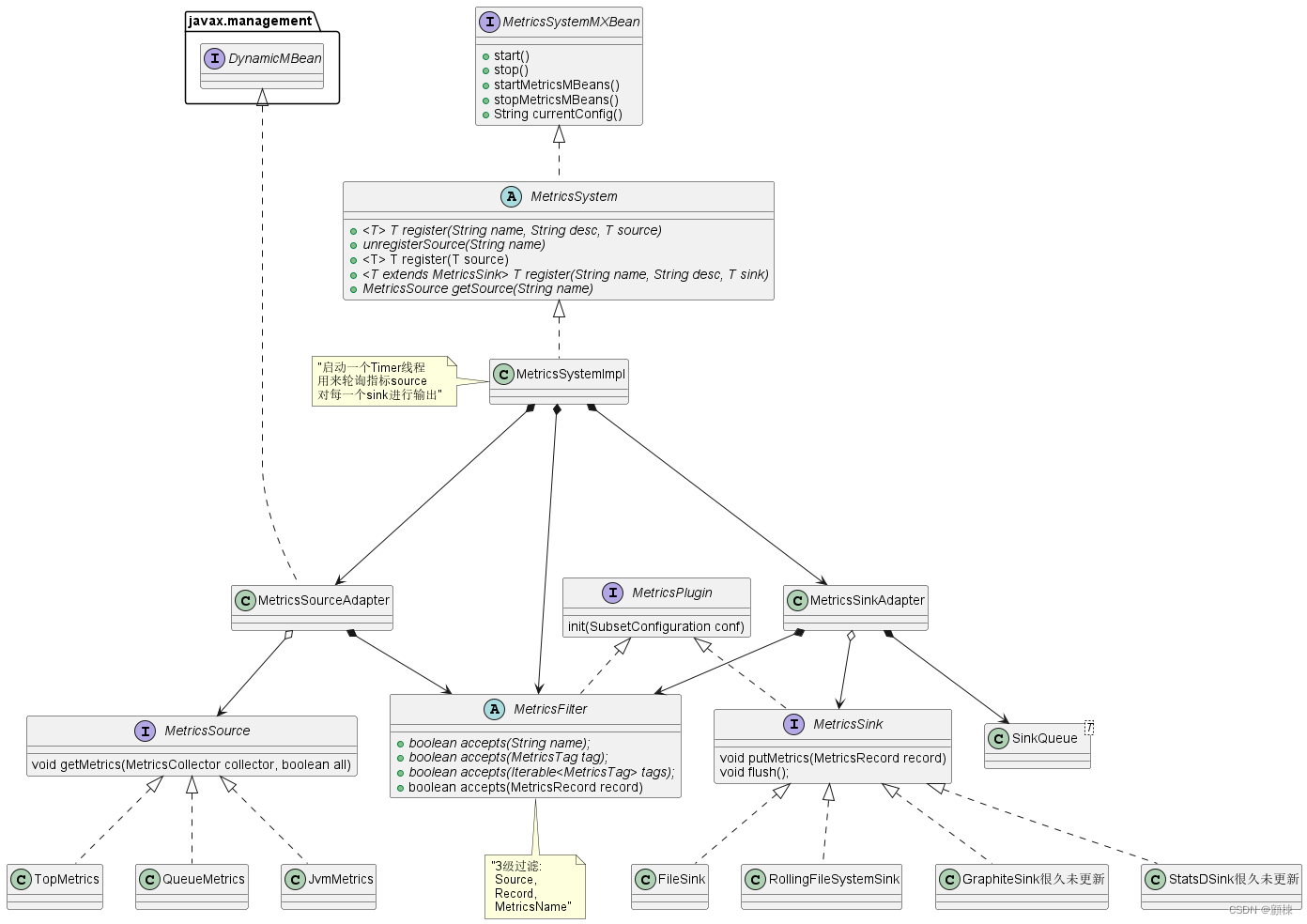
【Hadoop实战】Hadoop指标系统V2分析
Hadoop指标系统V2分析 文章目录 Hadoop指标系统V2分析架构主要组成部分根据图表解释数据流向指标过滤JMX的应用开启指标系统的组件指标项说明 使用HTTP(JMXJsonServlet)获取指标接口调用方式GET查询的逻辑数据的来源,以及更新的原理 架构 在…...
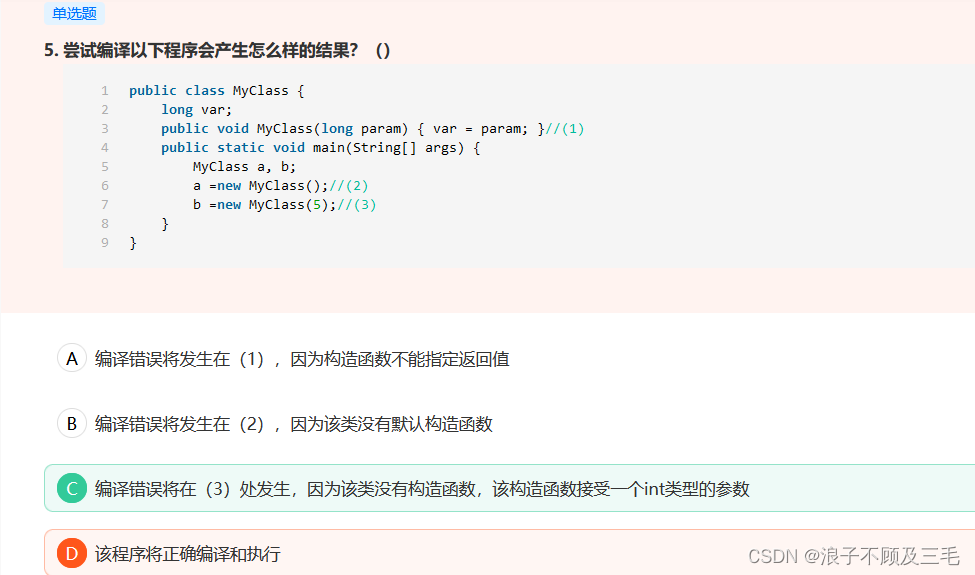
【java:牛客每日三十题总结-5】
java:牛客每日三十题总结 总结如下 总结如下 -Xmx:最大堆大小 -Xms:初始堆大小 -Xmn:年轻代大小 -XXSurvivorRatio:年轻代中Eden区与Survivor区的大小比值 年轻代5120m, Eden:Survivor3,Survivor区大小102…...

【Redis】set常用命令集合间操作内部编码使用场景
文章目录 前置知识常见命令SADDSMEMBERSSISMEMBERSCARDSPOPSMOVESREM 集合间操作SINTERSINTERSTORESUNIONSUNIONSTORESDIFFSDIFFSTORE 命令小结内部编码测试内部编码 使用场景 前置知识 集合类型也是保存多个字符串类型的元素的,但和列表类型不同的是,在…...

94. 二叉树的中序遍历 --力扣 --JAVA
题目 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。 解题思路 中序遍历的顺序为左中右;通过递归来遍历左子树、添加数据、遍历右子树; 代码展示 package zero.zero.nine;import java.util.ArrayList; import java.util.List;/*** …...
webpack babel
构建工具 简介 当我们习惯了在node中编写代码的方式后,在回到前端编写html、css、js这些东西会感觉到各种的不便。比如:不能放心的使用模块化规范(浏览器兼容性问题)、即使可以使用模块化规范也会面临模块过多时的加载问题。我们…...

autollm 指令设计
autollm 指令设计 可循环示意图文本 示意图AI解释可循环示意图 文本 示意图 # <|aos|>环境<|bos|>他人<|cos|>自己<|dos|>表示是否进行写python 代码来从外界获取辅助数据来重构 前面所有的信息<|eos|>代表是否生成python 代码控制各种外审设备…...

浙江大学漏洞报送证书
获取来源:edusrc(教育漏洞报告平台) url:主页 | 教育漏洞报告平台 兑换价格:20金币 获取条件:提交浙江大学任意中危或以上级别漏洞...

ROS 学习应用篇(三)服务Server学习之Server
话题Topic是订阅器与发布器节点之间的,而服务则是客户端(Client)和服务器(Server)间的,前者是异步的,后者是同步的。而且话题是单项的不需要服务器上线,而服务是双向的。在开启服务之…...

vue+css动画 实现文字的上下轮播切换
突然间碰到一个比较丝滑的特效,就研究了一下想把它实现出来。 效果:渐隐消失,底部往上走覆盖出现 以下是完整代码,复制粘贴即可运行 <template><div class="aaa"><divclass="page1":class="{ private-fade-out: prevIndex === 1…...
debian/ubuntu/windows配置wiregurad内网服务器(包含掉线自启动)
文章目录 前言一、服务器配置安装wireguard软件生成私钥公钥配置服务器参数配置服务器sysctl参数启动、停止服务端 二、用户端配置安装wireguard软件生成私钥公钥配置客户端参数启动、停止客户端配置服务开机启动 三、服务器添加、删除客户四、配置掉线自启动配置掉线自启动脚本…...

LeetCode146.LRU缓存
写了一个小时,终于把示例跑过了,没想到啊提交之后第19/22个测试用例没过 我把测试用例的输出复制在word上看看和我的有什么不同,没想到有18页的word,然后我一直检查终于找出了问题,而且这个bug真的太活该了,…...

5-7 使用函数求余弦函数的近似
实现一个函数,用下列公式求cos(x)的近似值,精确到最后一项的绝对值小于e:…...
Kotlin HashMap entries.filter过滤forEach
Kotlin HashMap entries.filter过滤forEach fun main(args: Array<String>) {val hashMap HashMap<String, Int>()hashMap["a"] 1hashMap["b"] 2hashMap["c"] 3println(hashMap)hashMap.entries.filter {println("filter $…...

css的预处理
CSS的预处理器是一种CSS的扩展,可以让开发者使用更加高效、灵活的方式来编写CSS代码。 常用的CSS预处理器包括: Sass:基于Ruby的CSS预处理器,提供了大量的函数和变量等扩展功能。 Less:基于JavaScript的CSS预处理器&…...

[云原生案例2.2 ] Kubernetes的部署安装 【单master集群架构 ---- (二进制安装部署)】网络插件部分
文章目录 1. Kubernetes的网络类别2. Kubernetes的接口类型3. CNI网络插件 ---- Flannel的介绍及部署3.1 简介3.2 flannel的三种模式3.3 flannel的UDP模式工作原理3.4 flannel的VXLAN模式工作原理3.5 Flannel CNI 网络插件部署3.5.1 上传flannel镜像文件和插件包到node节点3.5.…...

Go开发基础环境搭建
前面,我们写了下关于GO的入门简介,今天我们打算实操,在实操之前需要准备下基础环境。 IDE开发工具 GoLand 是一款由捷克软件开发公司 JetBrains 专为 Go 开发的跨平台商业 IDE。Goland 具有 Strong Code Insight、Navigation & Search、…...
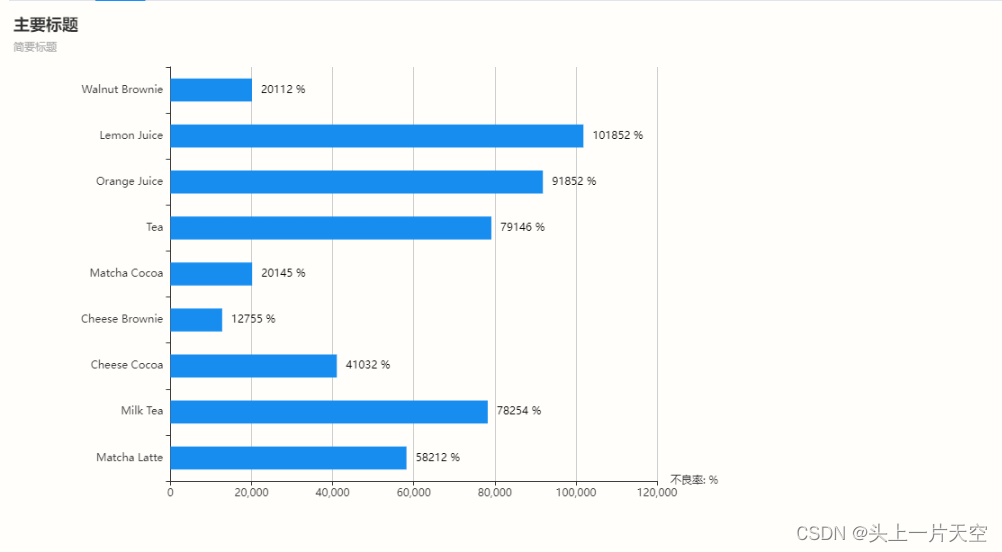
Vue简单使用Echart图表柱形图 vue使用柱形图 vue使用 echart图表柱形图 vue使用柱形图
Vue简单使用Echart图表柱形图 vue使用柱形图 vue使用 echart图表柱形图 vue使用柱形图 1、安装依赖2、页面Demo使用3、效果图 1、安装依赖 官方文档:https://echarts.apache.org/zh/option.html#title 官方在线示例:https://echarts.apache.org/exampl…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...
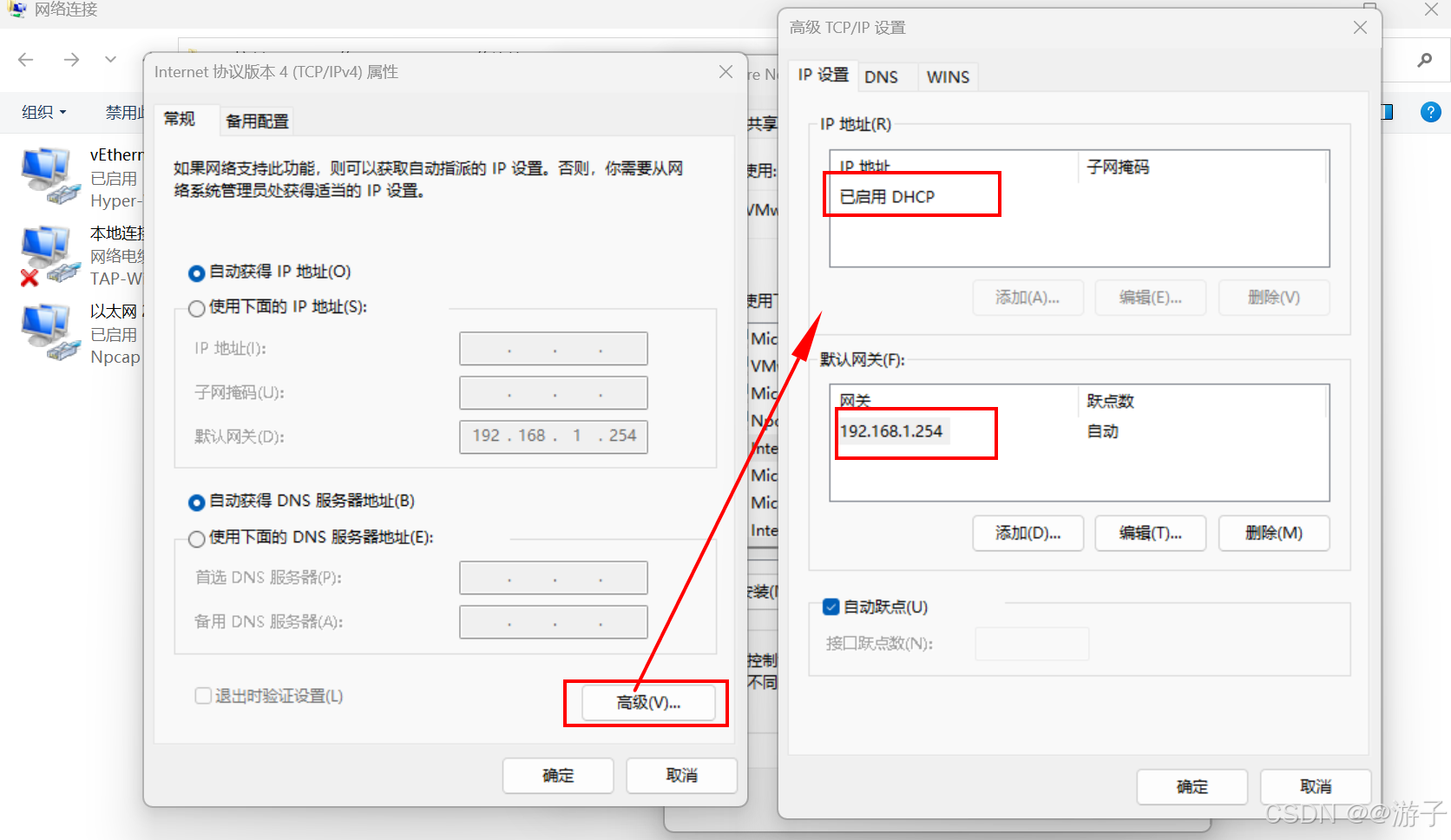
虚拟机网络不通的问题(这里以win10的问题为主,模式NAT)
当我们网关配置好了,DNS也配置好了,最后在虚拟机里还是无法访问百度的网址。 第一种情况: 我们先考虑一下,网关的IP是否和虚拟机编辑器里的IP一样不,如果不一样需要更改一下,因为我们访问百度需要从物理机…...

十二、【ESP32全栈开发指南: IDF开发环境下cJSON使用】
一、JSON简介 JSON(JavaScript Object Notation)是一种轻量级的数据交换格式,具有以下核心特性: 完全独立于编程语言的文本格式易于人阅读和编写易于机器解析和生成基于ECMAScript标准子集 1.1 JSON语法规则 {"name"…...

Java多线程从入门到精通
一、基础概念 1.1 进程与线程 进程是指运行中的程序。 比如我们使用浏览器,需要启动这个程序,操作系统会给这个程序分配一定的资源(占用内存资源)。 线程是CPU调度的基本单位,每个线程执行的都是某一个进程的代码的某…...

成工fpga(知识星球号)——精品来袭
(如需要相关的工程文件请关注知识星球:成工fpga,https://t.zsxq.com/DMeqH,关注即送200GB学习资料,链接已置顶!) 《孩子都能学会的FPGA》系列是成工完成的第一个系列,也有一年多的时…...

Git 使用大全:从入门到精通
Git 是目前最流行的分布式版本控制系统,被广泛应用于软件开发中。本文将全面介绍 Git 的各种功能和使用方法,包含大量代码示例和实践建议。 文章目录 Git 基础概念版本控制系统Git 的特点Git 的三个区域Git 文件状态 Git 安装与配置安装 GitLinuxmacOSWi…...
