pytorch基础语法问题
这里写目录标题
- pytorch基础语法问题
- shape
- torch.ones_like函数和torch.zeros_like函数
- y.backward(torch.ones_like(x), retain_graph=True)
- torch.autograd.backward
- 参数grad_tensors: z.backward(torch.ones_like(x))
- 来个复杂例子z.backward(torch.Tensor([[1., 0]])
- 更复杂例子
- 实际上,也可以通过 求均值 的形式将其转为标量
- retain_graph=True参数
- 在每次反向传播求导时,计算的梯度不会自动清零。如果进行多次迭代计算梯度而没有清零,那么梯度会在前一次的基础上叠加。需要使用 Tensor.grad.zero_()将梯度清零。x.grad.data.zero_()
- 非叶子节点(见上一篇文章)的梯度会默认被释放掉,除非用 retain_grad()函数明确指明保留其梯度。
- 一些援引
- 矩阵相乘
pytorch基础语法问题
shape
import torch
# 创建一个形状为(2, 3)的张量
x = torch.Tensor([[1, 2, 3], [4, 5, 6],[1,1,1],[2,2,2]])
print(len(x.shape))
print(x.shape[0])
# 遍历张量中的元素
for i in range(x.shape[0]):for j in range(x.shape[1]):print(x[i, j])
len(x.shape),维数,一般为二维
x.shape[0]:行数
x.shape[1]: 列数
2
4
tensor(1.)
tensor(2.)
tensor(3.)
tensor(4.)
tensor(5.)
tensor(6.)
tensor(1.)
tensor(1.)
tensor(1.)
tensor(2.)
tensor(2.)
tensor(2.)进程已结束,退出代码0
torch.ones_like函数和torch.zeros_like函数
返回一个形状与input相同且值全为1的张量。torch.ones_like(input)相当于torch.ones(input.size, dtype=input.dtype,layout=input.layout,device=input.device)
input = torch.rand(4, 6)
print(input)
# 生成与input形状相同、元素全为1的张量
a = torch.ones_like(input)
print(a)
# 生成与input形状相同、元素全为0的张量
b = torch.zeros_like(input)
print(b)

z.backward(torch.ones_like(z))
z.backward(torch.ones_like(z))中的torch.ones_like(z)相当于在对z进
行求导时,对z中的元素进行了求和操作,从而将其转为一个标量。
y.backward(torch.ones_like(x), retain_graph=True)
y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))
torch.autograd.backward
x = torch.tensor(1.0, requires_grad=True)
y = torch.tensor(2.0, requires_grad=True)
z = x**2+y
z.backward()
print(z, x.grad, y.grad)>>> tensor(3., grad_fn=<AddBackward0>) tensor(2.) tensor(1.)
可以z是一个标量,当调用它的backward方法后会根据链式法则自动计算出叶子节点的梯度值。
但是 如果遇到z是一个向量或者是一个矩阵的情况,这个时候又该怎么计算梯度呢? 这种情况我们需要定义grad_tensor来计算矩阵的梯度。在介绍为什么使用之前我们先看一下源代码中backward的接口是如何定义的:
torch.autograd.backward(tensors, grad_tensors=None, retain_graph=None, create_graph=False, grad_variables=None)
- tensor: 用于计算梯度的tensor。也就是说这两种方式是等价的:- torch.autograd.backward(z) == z.backward()
- grad_tensors: 在计算矩阵的梯度时会用到。他其实也是一个tensor,shape一般需要和前面的tensor保持一致。
- retain_graph: 通常在调用一次backward后,pytorch会自动把计算图销毁,所以要想对某个变量重复调用backward,则需要将该参数设置为True
- create_graph: 当设置为True的时候可以用来计算更高阶的梯度
- grad_variables: 这个官方说法是grad_variables’ is deprecated. Use - ‘grad_tensors’ instead.也就是说这个参数后面版本中应该会丢弃,直接使用grad_tensors就好了。
好了,参数大致作用都介绍了,下面我们看看pytorch为什么设计了grad_tensors这么一个参数,以及它有什么用呢?
参数grad_tensors: z.backward(torch.ones_like(x))
原则上,Pytorch不支持对张量的求导,即如果z是张量的话,需要先将其转为标量。
浏览了很多博客,给出的解决方案都是说在求导时,加一个torch.ones_like(z)的参数。
torch.ones_like(z)的作用。简而言之,torch.ones_like(z)相当于在对z进行求导时,对z中的元素进行求和操作,从而将其转为一个标量,便于后续的求导。
x = torch.ones(2,requires_grad=True)
z = x + 2
z.backward()>>> ...
RuntimeError: grad can be implicitly created only for scalar outputs

本质要得到 z对x求导, 但是已知的是X,Z ;一个矩阵对另一个矩阵求导,才能得到 每个z_partial 对x_partial的导数
其实,可以让sum(z_partial) 对于X求导,对xi 求偏导,就可以得到对应的z_partial
对x_partial的导数,,因为sum(z_partial) 对xi 求偏导,只有包含xi 的那一项在求导,其余与xi 无关的项
对xi求导为0
我们再仔细想想,对z求和不就是等价于z点乘一个一样维度的全为1的矩阵吗?即 ![[公式]](https://img-blog.csdnimg.cn/7da8693b5ae34f99a120ac60d76e7bba.png)
,而这个I也就是我们需要传入的grad_tensors参数。(点乘只是相对于一维向量而言的,对于矩阵或更高为的张量,可以看做是对每一个维度做点乘)
import torchx = torch.ones(2,3,requires_grad=True)
z = 2*x + 2
print(z)
print(z.sum())
# print(z.*torch.ones_like(x))
z.sum().backward()#或者z.backward(torch.ones_like(x)) 效果一样!
print(x.grad)'''
tensor([[4., 4., 4.],[4., 4., 4.]], grad_fn=<AddBackward0>)
tensor(24., grad_fn=<SumBackward0>)
tensor([[2., 2., 2.],[2., 2., 2.]])
'''来个复杂例子z.backward(torch.Tensor([[1., 0]])
x = torch.tensor([2., 1.], requires_grad=True).view(1, 2)
y = torch.tensor([[1., 2.], [3., 4.]], requires_grad=True)z = torch.mm(x, y)
print(f"z:{z}")
z.backward(torch.Tensor([[1., 0]]), retain_graph=True)
print(f"x.grad: {x.grad}")
print(f"y.grad: {y.grad}")>>> z:tensor([[5., 8.]], grad_fn=<MmBackward>)
x.grad: tensor([[1., 3.]])
y.grad: tensor([[2., 0.],[1., 0.]])
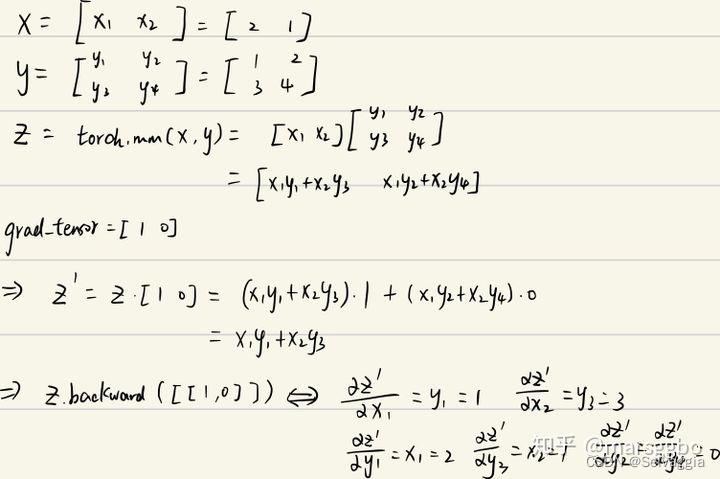
说了这么多,grad_tensors的作用其实可以简单地理解成在求梯度时的权重,因为可能不同值的梯度对结果影响程度不同,所以pytorch弄了个这种接口,而没有固定为全是1。引用自知乎上的一个评论:如果从最后一个节点(总loss)来backward,这种实现(torch.sum(y*w))的意义就具体化为 multiple loss term with difference weights 这种需求了吧
内容来源
看到这里我不由得想,会不会有更复杂的例子呢,万一 输入参数太多多维,导致得到的z不只是一个一维向量,是多维的矩阵,那么就是sum起来或者是点乘一个和z尺寸相同的全1矩阵咯,反正,z是一定是要被处理成一个标量才能进行求导
(原则上,Pytorch不支持对张量的求导,即如果z是张量的话,需要先将其转为标量。)
更复杂例子
import torchx = torch.tensor(3.,requires_grad=True)
p = torch.ones(2,2,requires_grad=True)y = x*x
z = 2*y+2*p*p
# [
# [1,1],
# [1,1]
# ]
z.backward(torch.ones_like(z))
# # z = z.sum() # 与下面的torch.sum(z)作用相同,即z中所有元素的和。
# z = torch.sum(z)
# z.backward()
print(x.grad)
print(p.grad)
# print(y.grad) # backward()无法对非叶子节点求导# 知识点汇总:
# 原则上,Pytorch不支持对张量的求导,即如果z是张量的话,需要先将其转为标量。
# 就这个例子来说,z.backward(torch.ones_like(z))中的torch.ones_like(z)相当于在对z进行求导时,对z中的元素进行了求和操作,从而将其转为一个标量。



pp,张量相乘,对应位置的元素相乘,torch.mul()和 ,广播机制
z = 2y+2p*p,张量相加,广播机制,y这个标量被生生广播 扩维了,
当 z.sum().backward(),求和再对x求导,这个导数就大了不少(广播机制之后再求和,计算过程中标量y维数扩大了四倍,导致z对y的导数也扩大了四倍,夸大了,不合适
这么大,对x求导不太公正啊
实际上,也可以通过 求均值 的形式将其转为标量
z = z.mean() # z中所有元素的均值
z.backward()
该部分来自于此处
retain_graph=True参数
当我们计算梯度时,PyTorch会自动根据计算图反向传播梯度来更新模型参数。但是,当我们的计算图比较复杂,或者需要多次反向传播时,我们可能需要使用retain_graph参数来保存计算图。
retain_graph表示在进行反向传播计算梯度的时候,是否保留计算图。如果设置为True,则计算图将被保留,可以在之后的操作中进行多次反向传播计算。如果为False,则计算图将被清空。这是为了释放内存并防止不必要的计算。
pytorch进行一次backward之后,各个节点的值会清除,这样进行第二次backward会报错,因为虽然计算节点数值保存了,但是计算图结构被释放了,如果加上retain_graph==True后,可以再来一次backward。
import torch# 定义张量
x = torch.ones(2, 2, requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()
print(x.grad)
# print(y) 全3矩阵
# print(z) #全27矩阵
# 计算梯度
out.backward(retain_graph=True)
print(x.grad)
# 再次计算梯度
z.backward(torch.ones_like(z))
print(x.grad)None
tensor([[4.5000, 4.5000],[4.5000, 4.5000]])
tensor([[22.5000, 22.5000],[22.5000, 22.5000]])

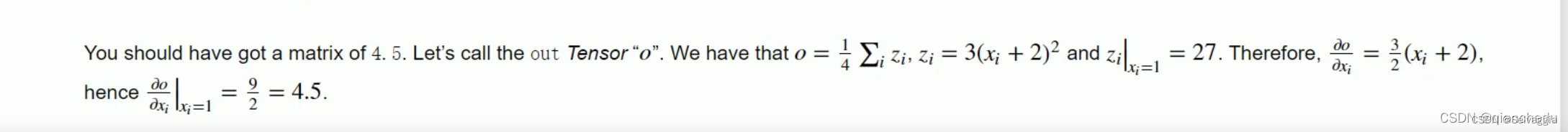
z对x求导,在x为全1矩阵之处应该是18,但你会发现代码运行结果是22.5,很没有厘头,其实是因为 梯度累加
如何解决呢
x.grad.data.zero_()
在每次反向传播求导时,计算的梯度不会自动清零。如果进行多次迭代计算梯度而没有清零,那么梯度会在前一次的基础上叠加。需要使用 Tensor.grad.zero_()将梯度清零。x.grad.data.zero_()
import torch# 定义张量
x = torch.ones(2, 2, requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()
print(x.grad)
# print(y) 全3矩阵
# print(z) #全27矩阵
# 计算梯度
out.backward(retain_graph=True)
print(x.grad)
x.grad.data.zero_()
# 再次计算梯度
z.backward(torch.ones_like(z))
print(x.grad)None
tensor([[4.5000, 4.5000],[4.5000, 4.5000]])
tensor([[18., 18.],[18., 18.]])
再来个例子
import torchw = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
# y=(x+w)*(w+1)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)# 反向传播求导数
# torch.autograd.backward(y)
y.backward(retain_graph=True)
print("w's grad: {}\\nx's grad: {}".format(w.grad, x.grad))
# print("a's grad: {}".format(a.grad))# 清零梯度
# w.grad.zero_()
# x.grad.zero_()# 第二次求导
y.backward()
print("w's grad: {}\\nx's grad: {}".format(w.grad, x.grad))
输出结果:
w's grad1: tensor([5.])
x's grad1: tensor([2.])
w's grad2: tensor([10.])
x's grad2: tensor([4.])可以,如果注释掉 grad.zero() 相关的代码,那么第二次计算得到的导数就叠加到了第一次结果之上。
非叶子节点(见上一篇文章)的梯度会默认被释放掉,除非用 retain_grad()函数明确指明保留其梯度。
print("a's grad: {}".format(a.grad))
输出结果:
a’s grad: None
如这里如果我们输出非叶子节点 的梯度,显示为 None。
此段来自:backward()函数注意事项
一些援引
待看
pytorch中retain_graph==True的作用说明(详细例子+踩坑说明)

本来有个问题,啥叫释放,怎么释放,只要最后一次一次backward不设置retain_graph==True,就算释放
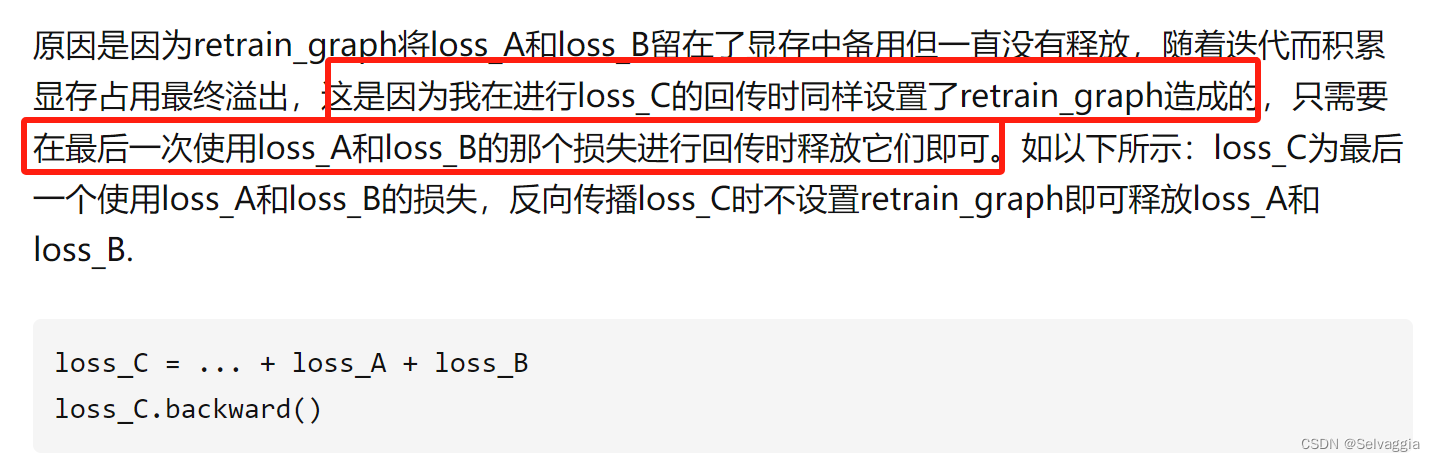
以上是这篇的意思
梯度会叠加,我看到有代码 在循环里面使用backward,也没用 retain_graph==True,计算树没被释放?还有,想必需要用到梯度叠加?
矩阵相乘
pytorch中的矩阵乘法操作(总结的好!简明精要
pytorch中的矩阵乘法操作:
torch.mm()
- 只适合于二维张量的矩阵乘法
- m x n, n x p -> m x p
torch.bmm()
- 只适合于三维张量的矩阵乘法,与torch.mm类似,但多了一个batch_size维度。
- b x m x n, b x n x p -> b x m x p
torch.mul()和*
- ⭐ torch.mul()和*等价。
- 张量对应位置元素相乘。
- 将输入张量input的每个元素与另一个向量or标量other相乘,返回一个新的张量out,两者维度需满足广播规则
torch.dot()
向量点积:两向量对应位置相乘然后全部相加。只能支持两个一维向量。
torch.mv(), @, torch.matmul()
相关文章:

pytorch基础语法问题
这里写目录标题 pytorch基础语法问题shapetorch.ones_like函数和torch.zeros_like函数y.backward(torch.ones_like(x), retain_graphTrue)torch.autograd.backward参数grad_tensors: z.backward(torch.ones_like(x))来个复杂例子z.backward(torch.Tensor([[1., 0]])更复杂例子实…...
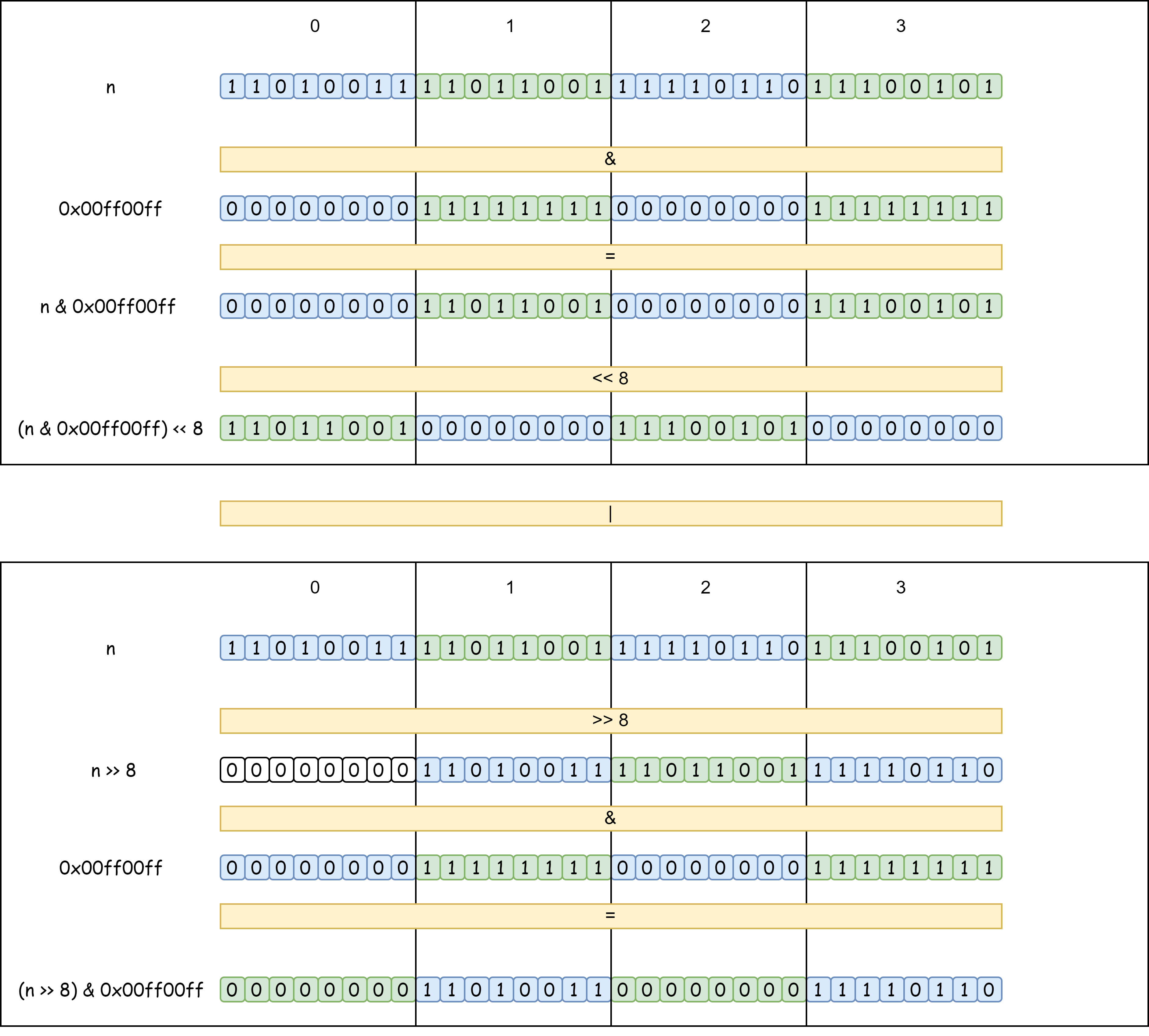
【面试经典150 | 】颠倒二进制位
文章目录 写在前面Tag题目来源题目解读解题思路方法一:逐位颠倒方法二:分治 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于…...

十分钟了解自动化测试
自动化测试 自动化测试的定义:使用一种自动化测试工具来验证各种软件测试的需求,它包括测试活动的管理与实施、测试脚本的开发与执行。 自动化测试只是测试工作的一部分,是对手工测试的一种补充; 自动化测试绝不能代替手工测试;多数情况下&…...

Redis配置文件
Redis可以在没有配置文件的情况下使用内置的默认配置启动,但是这种设置仅推荐用于测试和开发。 配置Redis的正确方法是提供一个Redis配置文件,通常称为 redis.conf 。 通过命令行传递参数启动 你也可以直接使用命令行传递Redis配置参数。这对于测试非…...

[量化投资-学习笔记009]Python+TDengine从零开始搭建量化分析平台-KDJ
技术分析有点像烹饪,收盘价、最值、成交量等是食材;均值,移动平均,方差等是烹饪方法。随意组合一下就是一个技术指标。 KDJ又称随机指标(随机这个名字起的很好)。KDJ的计算依据是最高价、最低价和收盘价。…...

Activiti6工作流引擎:Form表单
表单约等于流程变量。StartEvent 有一个Form属性,用于关联流程中涉及到的业务数据。 一:内置表单 每个节点都可以有不同的表单属性。 1.1 获取开始节点对应的表单 Autowired private FormService formService;Test void delopyProcess() {ProcessEngi…...

Fortran 中的指针
Fortran 中的指针 指针可以看作一种数据类型 指针存储与之关联的数据的内存地址变量指针:指向变量数组指针:指向数组过程指针:指向函数或子程序指针状态 未定义未关联 integer, pointer::p1>null() !或者 nullify(p1) 已关联 指针操作 指…...
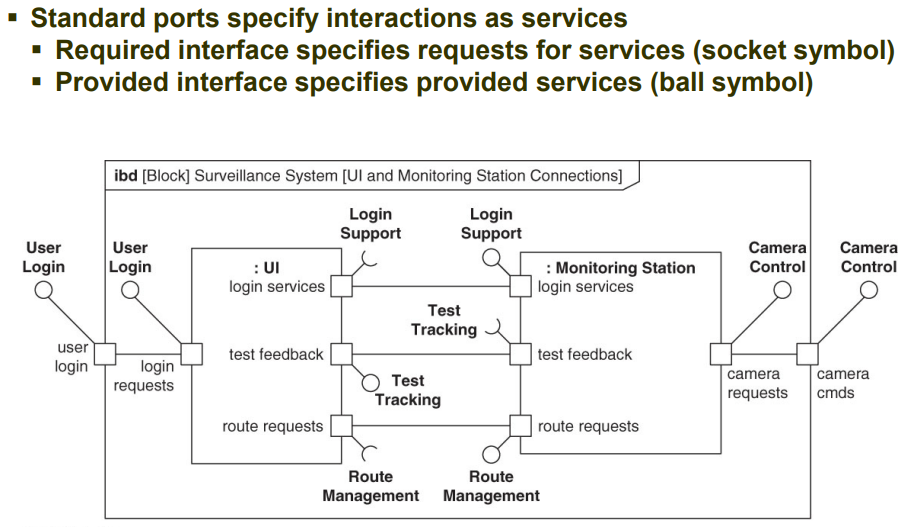
第七章 块为结构建模 P4|系统建模语言SysML实用指南学习
仅供个人学习记录 这部分感觉很模糊,理解的不好,后面的图也没画了,用到的时候再来翻书 应用端口实现接口建模 端口port表示了块边界上的一个访问点,也可以是由该块分类的任何组成或引用边界上的可访问点。一个块可以有多个端口规…...
提升中小企业效率的不可或缺的企业云盘网盘
相比之大型企业,中小型企业在挑选企业云盘工具更注重灵活性和成本。那么市面上有哪些企业云盘产品更适合中小企业呢? 说起中小企业不能错过的企业云盘网盘,Zoho Workdrive企业云盘绝对榜上有名! Zoho Workdrive企业云盘为用户提…...

Web 安全之时序攻击 Timing Attack 详解
目录 什么是 Timing Attack 攻击? Timing Attack 攻击原理 Timing Attack 攻击的几种基本类型 如何防范 Timing Attack 攻击 小结 什么是 Timing Attack 攻击? Timing Attack(时序攻击)是一种侧信道攻击(timing s…...

【objectarx.net】定时器的使用
【objectarx.net】定时器的使用...

C++:容器list的介绍及使用
目录 1.list的介绍及使用 1.1 list的介绍 1.2 list的使用 1.2.1 list的构造 1.2.2 list iterator 的使用 1.2.3 list capacity 容量 1.2.4 list element access 访问list元素 1.2.5 list modifiers 修改 1.2.6 迭代器失效 1.list的介绍及使用 1.1 list的介绍 C官网 …...
元核云亮相金博会,智能质检助力金融合规
11月初,第五届中新(苏州)数字金融应用博览会|2023金融科技大会在苏州国际博览中心举办,围绕金融科技发展热点领域及金融行业信息科技领域重点工作,分享优秀实践经验,探讨数字化转型路径与未来发…...
Harmony 应用开发的知识储备
Harmony 应用开发的知识储备 前言正文一、DevEco Studio版本二、手机版本① 环境变量 三、API版本四、开发语言五、运行调试 前言 这里先说明一点,如果你对Android应用开发很熟悉,那么做Harmony应用开发也可以驾轻就熟,只不过在此之前你需要知…...
104. 二叉树的最大深度)
(层次遍历)104. 二叉树的最大深度
原题链接:(层次遍历)104. 二叉树的最大深度 思路: 使用层序遍历模板,遍历每一层 hight1 返回hight即可 全代码: class Solution { public:int maxDepth(TreeNode* root) {queue<TreeNode*> que;int hight 0;if(root NU…...
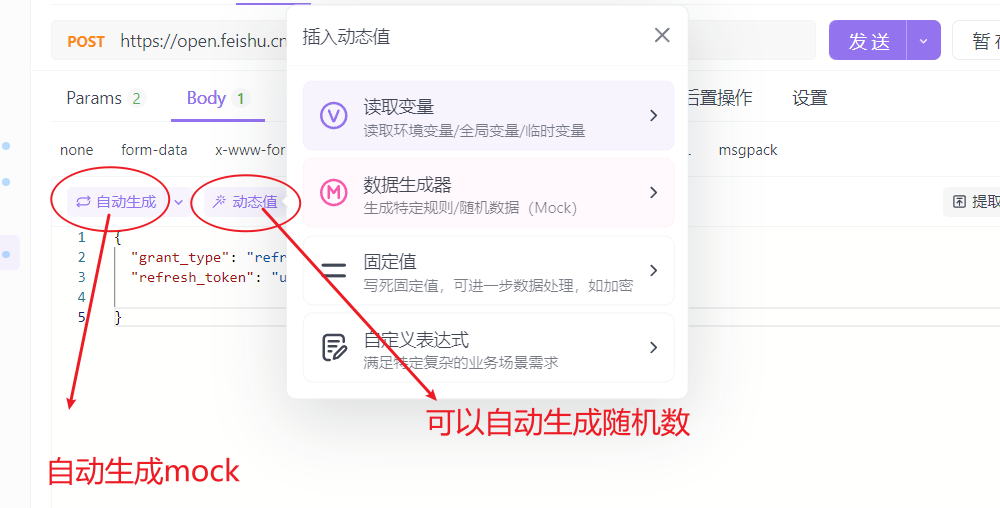
【api_fox】ApiFox简单操作
1、get和post请求的区别?2、接口定义时的传参格式?3、保存接口文档 apifox当中接口文档的设计和接口用例的执行是分开的。 1、get和post请求的区别? 2、接口定义时的传参格式? 3、保存接口文档 就生成如下的接口文档。...
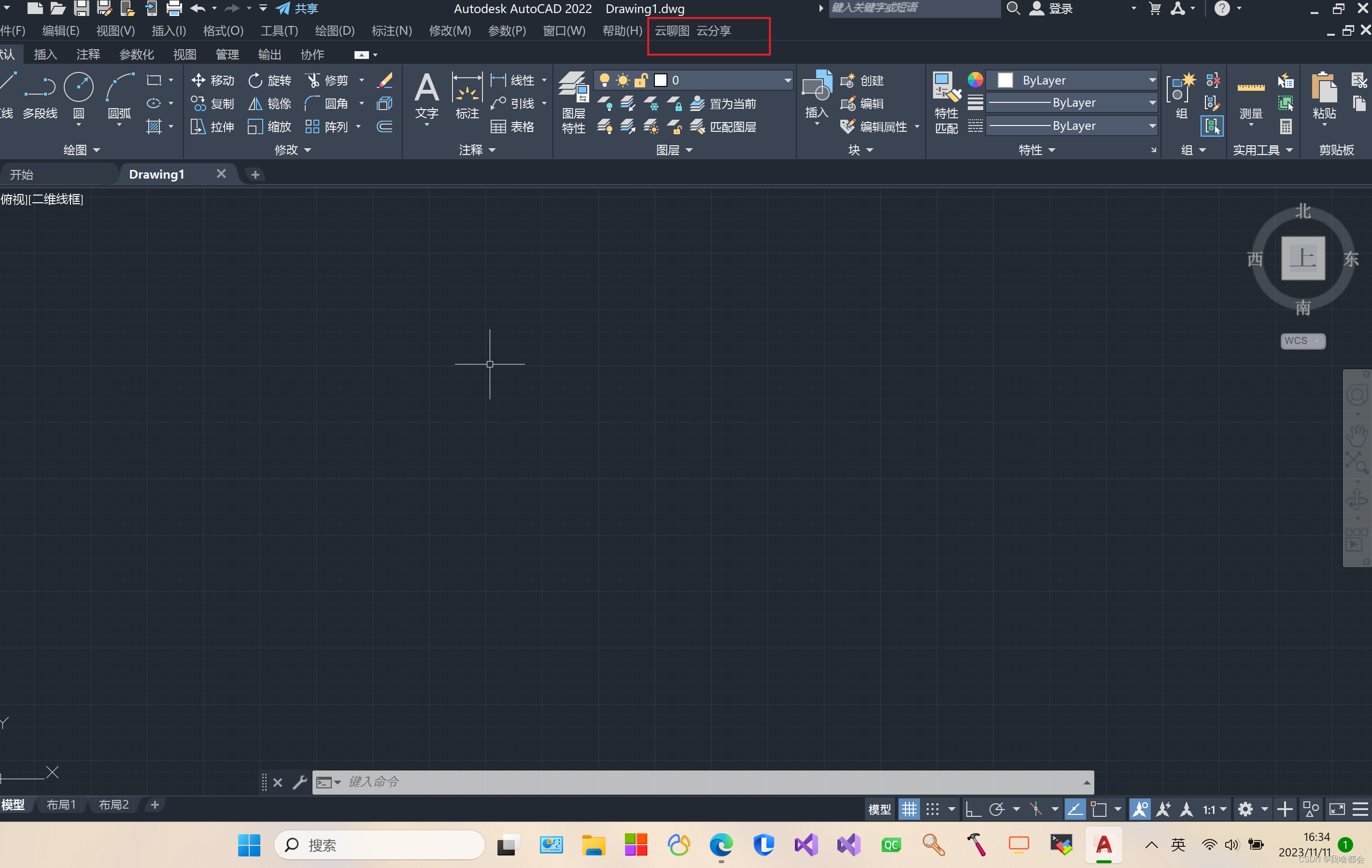
给CAD中添加自定义菜单CUIX
本文以AutoCAD2020为例,介绍如何添加自定义菜单。 打开AutoCAD2020,在命令行执行CUI并回车,出现菜单 进入菜单编辑界面 点击传输,然后新建 在菜单上右键,添加自定义菜单 点击保存,即可存为cuix文件。之后…...

Qt重启windows服务
日常开发中,会遇到改变某个服务的参数,并进行重启(例如Redis断电恢复机制) 需要程序拥有UAC权限,并且调用如下API才能对windows服务进行重启: #include "windows.h"#pragma comment(lib, "…...

OD机考真题:宜居星球改造计划
题目 2XXX 年,人类通过对火星的大气进行宜居改造分析,使得火星已在理论上具备人类宜居的条件; 由于技术原因,无法一次性将火星大气全部改造,只能通过局部处理形式; 假设将火星待改造的区域为 row * column_row_∗_column_ 的网格,每个网格有 3 个值,宜居区、可改造区、…...

Python每日练习:20个常用代码,初学者也可以自己实现!
文章目录 前言20个代码1.重复元素判定2.字符元素组成判定3.内存占用4.字节占用5.打印 N 次字符串6.大写第一个字母7.分块8.压缩9.解包10.链式对比11.逗号连接12.元音统计13.首字母小写14.展开列表15.列表的差16.通过函数取差17.链式函数调用18.检查重复项19.合并两个字典20.将两…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
