CTFer成长之路之逻辑漏洞
逻辑漏洞CTF
访问url:
http://1b43ac78-61f7-4b3c-9ab7-d7e131e7da80.node3.buuoj.cn/
登录页面用随意用户名+密码登录

访问url:
http://1b43ac78-61f7-4b3c-9ab7-d7e131e7da80.node3.buuoj.cn/user.php
登陆后有商品列表,共三个商品,点击购买flag

钱不够

另两个商品购买会显示各自对应的内容,并在多次购买后也会提示Money Not Enough
结合对应的金额不难发现存在初始金额,并且金额有限。在进行购买时,url形如:buy.php?cost=200&goods=2,
其中便有消费金额的参数,后端根据消费金额直接对余额进行增减将消费金额修改为负数时,便能够使余额增长:buy.php?cost=-200&goods=2,将数字调大便可使余额能购买Flag:
构造payload:buy.php?cost=-20000&goods=1
此时便能够正常购买Flag

文笔生疏,措辞浅薄,望各位大佬不吝赐教,万分感谢。
免责声明:由于传播或利用此文所提供的信息、技术或方法而造成的任何直接或间接的后果及损失,均由使用者本人负责, 文章作者不为此承担任何责任。
转载声明:儒道易行 拥有对此文章的修改和解释权,如欲转载或传播此文章,必须保证此文章的完整性,包括版权声明等全部内容。未经作者允许,不得任意修改或者增减此文章的内容,不得以任何方式将其用于商业目的。
博客:
https://rdyx0.github.io/先知社区:
https://xz.aliyun.com/u/37846SecIN:
https://www.sec-in.com/author/3097CSDN:
https://blog.csdn.net/weixin_48899364?type=blog公众号:
https://mp.weixin.qq.com/mp/appmsgalbum?__biz=Mzg5NTU2NjA1Mw==&action=getalbum&album_id=1696286248027357190&scene=173&from_msgid=2247485408&from_itemidx=1&count=3&nolastread=1#wechat_redirectFreeBuf:
https://www.freebuf.com/author/%E5%9B%BD%E6%9C%8D%E6%9C%80%E5%BC%BA%E6%B8%97%E9%80%8F%E6%8E%8C%E6%8E%A7%E8%80%85相关文章:

CTFer成长之路之逻辑漏洞
逻辑漏洞CTF 访问url: http://1b43ac78-61f7-4b3c-9ab7-d7e131e7da80.node3.buuoj.cn/ 登录页面用随意用户名密码登录 访问url: http://1b43ac78-61f7-4b3c-9ab7-d7e131e7da80.node3.buuoj.cn/user.php 登陆后有商品列表,共三个商品,点击购买flag 钱…...
)
入门力扣自学笔记238 C++ (题目编号:1144)
1144. 递减元素使数组呈锯齿状 题目: 给你一个整数数组 nums,每次 操作 会从中选择一个元素并 将该元素的值减少 1。 如果符合下列情况之一,则数组 A 就是 锯齿数组: 每个偶数索引对应的元素都大于相邻的元素,即 A…...

蓝桥杯-寒假作业
没有白走的路,每一步都算数🎈🎈🎈 题目描述: 有四个等式,每个等式的运算规则已经定好了,也就是我们常见的小学的四则运算,但是能够用来四则运算的数字非常有限,包括1~13…...
测试用例篇
1.测试用例的意义 测试用例(Test Case)是为了实施测试而向被测试的系统提供的一组集合,这组集合包含:测试环境、操作步骤、测试数据、预期结果等要素。 测试用例的意义是为了帮助测试人员了解测什么,怎么测 eg&#x…...

自动驾驶自主避障概况
文章目录前言1. 自主避障在自动驾驶系统架构中的位置2. 自主避障算法分类2.1 人工势场法(APF)2.1.1引力势场的构建2.1.2斥力势场的构建2.1.3人工势场法的改进2.2 TEB(Timed-Eastic-Band, 定时弹性带)2.3 栅格法2.4 向量场直方图(V…...

Python实用的库排名…
Python 是一个功能强大的编程语言,有着丰富的第三方库和模块,可以帮助你解决各种各样的问题。以下是一些比较厉害的 Python 库: NumPy:一个强大的数值计算库,提供了高效的数组和矩阵操作功能。 Pandas:提供…...
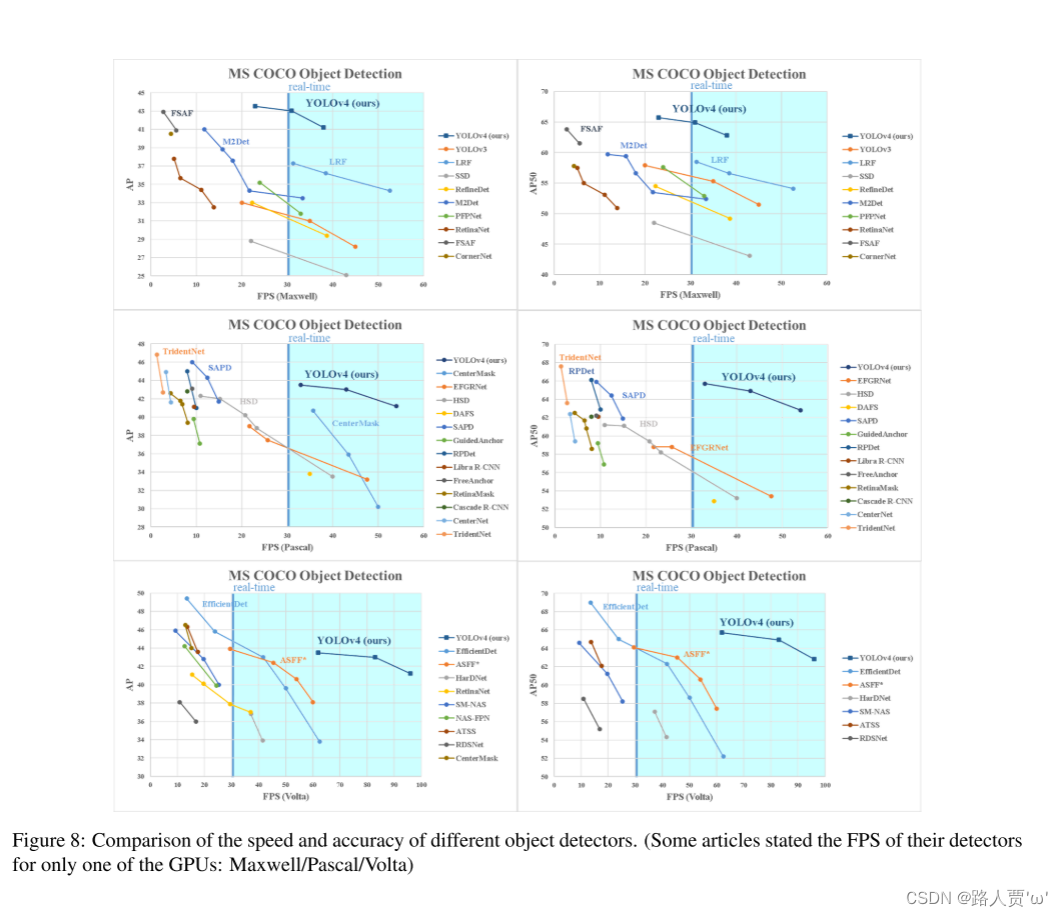
【YOLO系列】YOLOv4论文超详细解读1(翻译 +学习笔记)
前言 经过上一期的开篇介绍,我们知道YOLO之父Redmon在twitter正式宣布退出cv界,大家都以为YOLO系列就此终结的时候,天空一声巨响,YOLOv4闪亮登场!v4作者是AlexeyAB大神,虽然换人了,但论文中给出…...
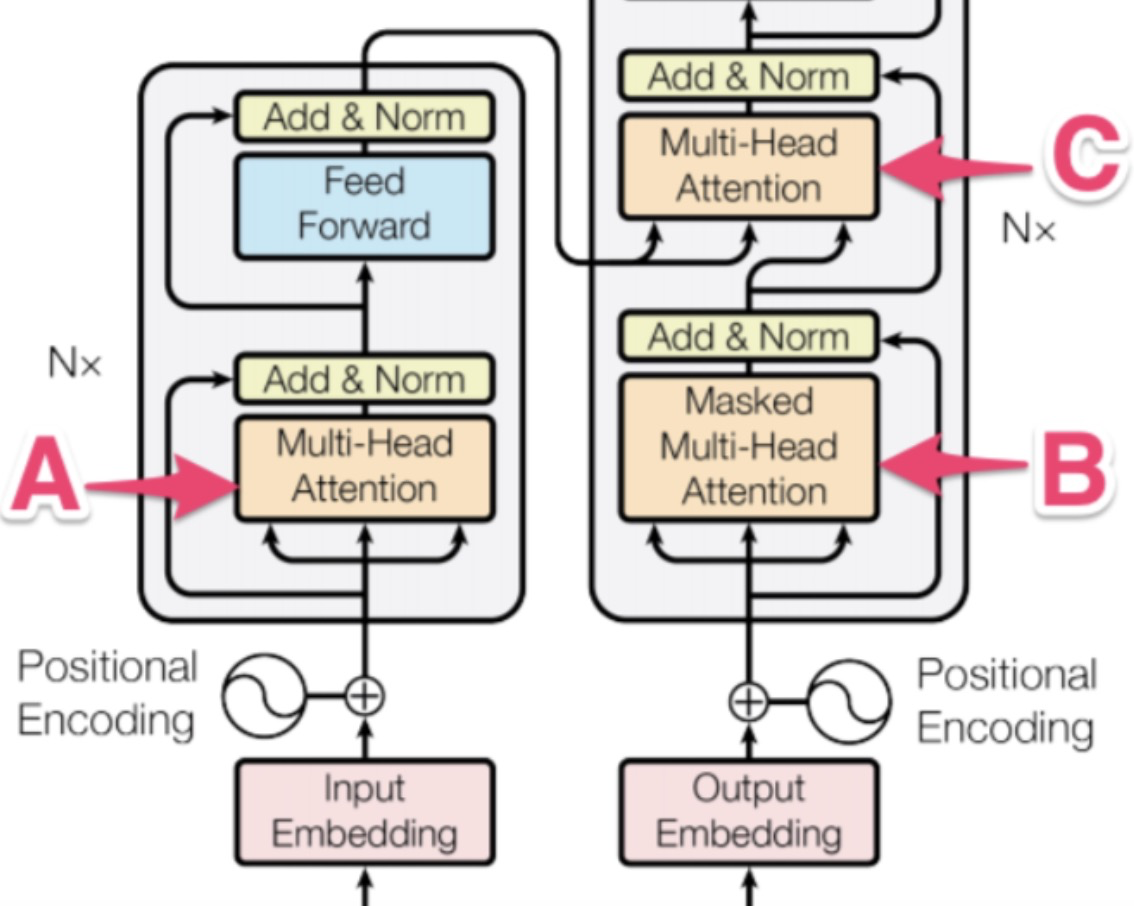
【神经网络】Transformer基础问答
1.Transforme与LSTM的区别 transformer和LSTM最大的区别就是LSTM的训练是迭代的,无法并行训练,LSTM单元计算完T时刻信息后,才会处理T1时刻的信息,T 1时刻的计算依赖 T-时刻的隐层计算结果。而transformer的训练是并行了࿰…...

制定防火墙策略的步骤和建议
制定防火墙策略是保护企业网络环境安全的关键一步。下面是一些制定防火墙策略的步骤和建议,供参考: 识别网络资产:确定企业网络环境中所有的网络资产,包括服务器、应用程序、数据库、移动设备和终端用户设备等,并进行…...
新必应(New Bing)国内申请与使用教程
微软的新必应(New Bing)基于GPT4模型,比ChatGPT的GPT3.5模型领先半个世代。并且集成了Edge浏览器的数据资源,功能更加强大。经过不断的踩坑,终于申请到了New Bing的使用权限,且国内网络也能够正常使用&…...
博客系统——项目测试报告
目录 前言 博客系统——项目介绍 1、测试计划 1.1、功能测试 1.1.1、编写测试用例 1.1.2、实际执行步骤 1.2、使用Selenium进行Web自动化测试 1.2.1、引入依赖 1.2.2、提取共性,实现代码复用 1.2.3、创建测试套件类 1.2.4、博客登录页自动化测试 1.2.5、…...
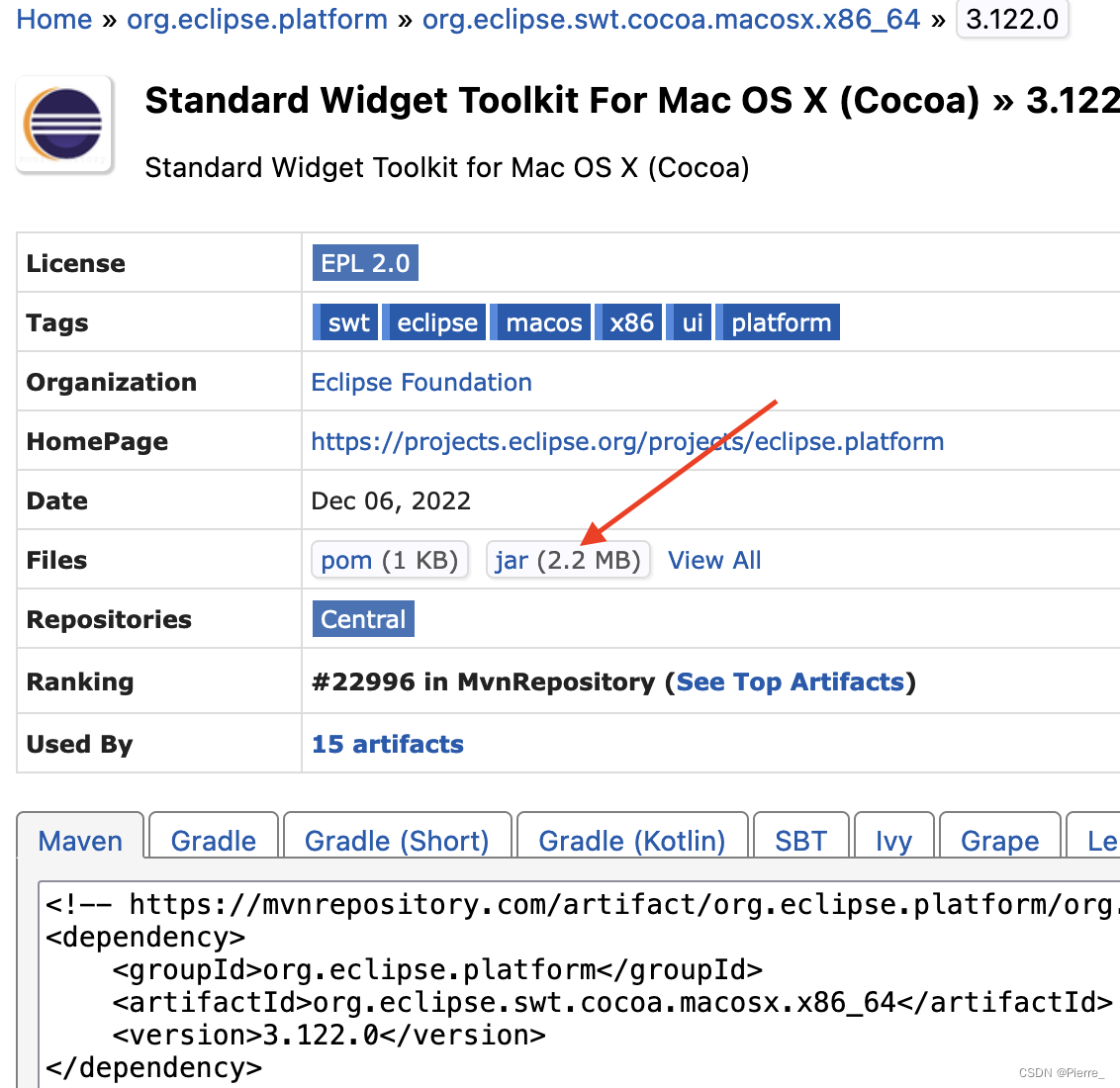
Macbook M1 安装PDI(Kettle) 9.3
Macbook M1 安装PDI(Kettle) 9.3 当前 PDI(Kettle)最新版为9.3,依赖Java JDK 11。因为没有专门用于 M1的程序,需要下载并安装x86_64架构的JDK及依赖软件,并 “强制在Intel模式下运行shell” 的方式来实现 Kettle 的正…...
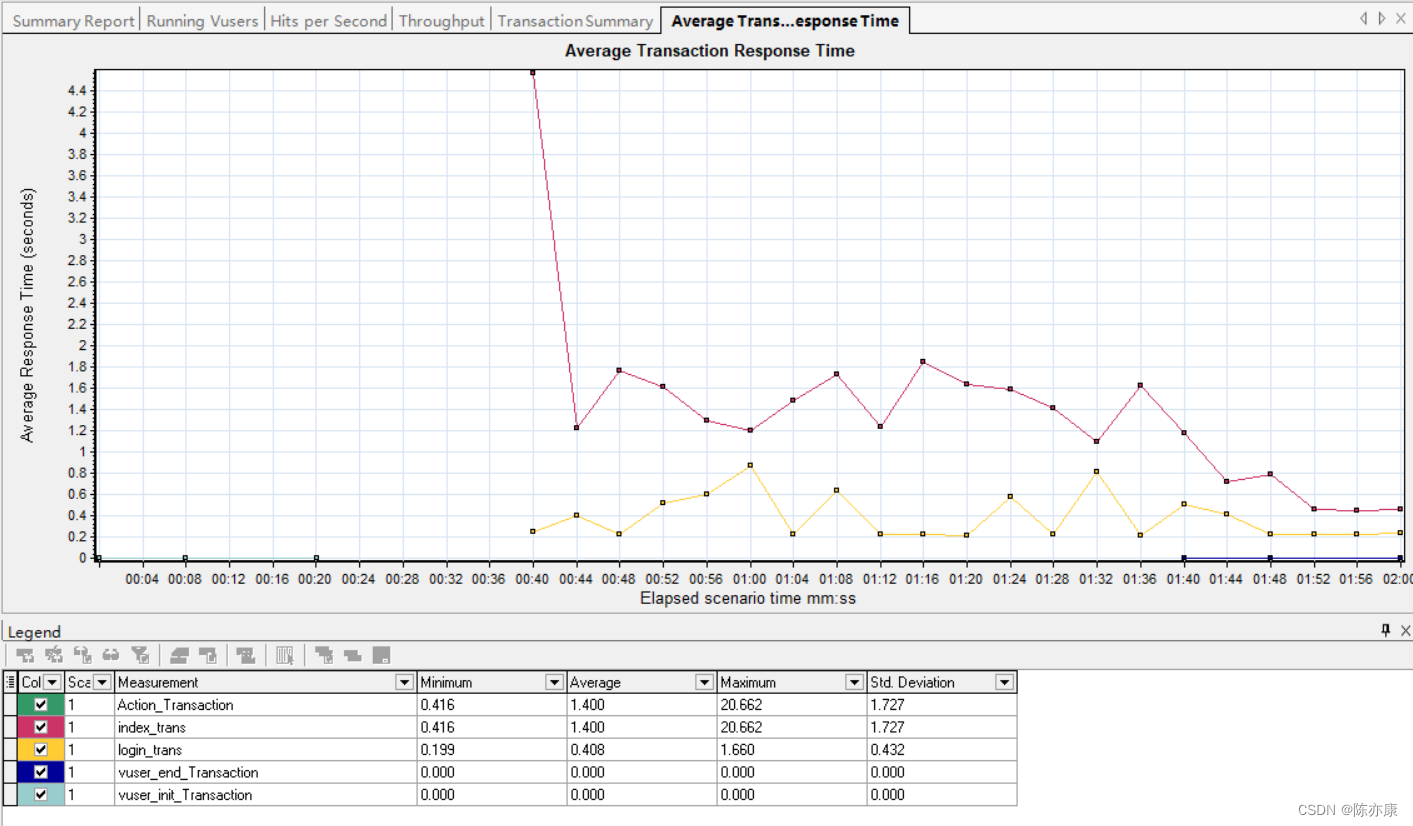
机器学习——模型评估
在学习得到的模型投放使用之前,通常需要对其进行性能评估。为此,需使用一个“测试集”(testing set)来测试模型对新样本的泛化能力,然后以测试集上的“测试误差( tootino error)作为泛化误差的近似。我们假设测试集是从样本真实分…...
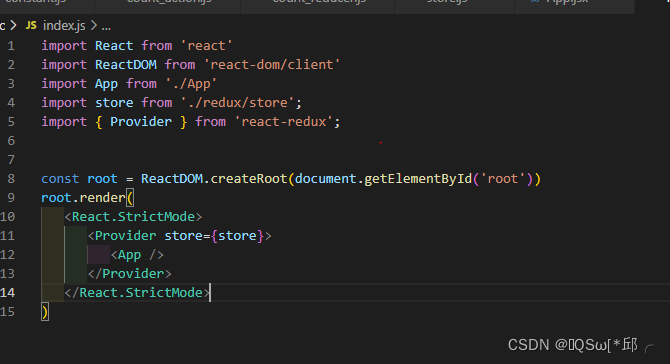
react react-redux学习记录
react react-redux学习记录1.原理2.怎么用呢2.1 容器组件2.2UI组件2.3 App.jsx3.简化3.1简写mapDispatch3.2 Provider组件的使用3.3整合UI组件和容器组件1.原理 UI组件:不能使用任何redux的api,只负责页面的呈现、交互等。 容器组件:负责和redux通信&…...
nodejs环境配置
啥是node.js 简单理解就是js运行环境 啥是npm 简单理解就是nodejs包管理工具,全称Node Package Manager 啥是cnpm npm的开源镜像,在国内使用cnpm替代npm可以起到加速的效果 https://npmmirror.com/ ①安装node.js https://nodejs.org/en/download/ 下载…...

数据治理之元数据管理Atlas
数据治理之元数据管理的利器——Atlas 一、数据治理与元数据管理 1.1 背景 为什么要做数据治理? 业务繁多,数据繁多,业务数据不断迭代。人员流动,文档不全,逻辑不清楚,对于数据很难直观理解,…...

15 Nacos客户端实例注册源码分析
Nacos客户端实例注册源码分析 实例客户端注册入口 流程图: 实际上我们在真实的生产环境中,我们要让某一个服务注册到Nacos中,我们首先要引入一个依赖: <dependency><groupId>com.alibaba.cloud</groupId>&l…...

C++将派生类赋值给基类(向上转型)
1.将派生类对象赋值给基类对象 #include <iostream> using namespace std;//基类 class A{ public:A(int a); public:void display(); public:int m_a; }; A::A(int a): m_a(a){ } void A::display(){cout<<"Class A: m_a"<<m_a<<endl; }//…...

使用Platform Designer创建Nios II 最小系统
Nios II简介 Nios II 软核处理器十多年前就有了,它和xilinx的MicroBlaze类似,性能相比硬核处理器要差得多,工程应用也不是很多,那还有必须学习一下吗?我个人认为了解一下Nios II开发流程,对intel FPGA开…...
CD销售管理系统
技术:Java、JSP等摘要:二十一世纪是一个集数字化,网络化,信息化的,以网络为核心的社会。中国的网民充分领略到“畅游天地间,网络无极限” 所带来的畅快。随着Internet的飞速发展,使得网络的应用…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
