邻接矩阵储存图实现深度优先遍历(C++)
目录
基本要求:
图的结构体:
图的构造:
图的深度优先(DFS):
图的打印输出:
完整代码:
测试数据:
运行结果:
通过给出的图的顶点和边的信息,构建无向图的邻接矩阵存储结构。在此基础上,从A顶点开始,对无向图进行深度优先遍历,输出遍历序列。
基本要求:
(1)从测试数据读入顶点和边信息,建立无向图邻接矩阵存储结构;
(2)把构建好的矩阵输入显示;
(3)从A顶点开始,编写DFS深度优先遍历算法;
(4)输出深度优先遍历序列。
图的结构体:
typedef char Vertextype;//顶点数据类型
typedef int Arctype;//边权值类型
typedef struct
{Vertextype vexs[mvnum];//顶点表Arctype arcs[mvnum][mvnum];//邻接矩阵int vexnum, arcnum;//当前图的点数和边数
}AMGraph;
图的构造:
bool Creategraph(AMGraph& G)
{cin >> G.vexnum >> G.arcnum;//输入总顶点数,总边数for (int i = 0; i < G.vexnum; i++){cin >> G.vexs[i];//依次输入点的信息mp[G.vexs[i]]=0;//辅助数组,是否访问过该点,0表示没访问过}for (int i = 0; i < G.vexnum; i++)//初始化邻接矩阵for (int j = 0; j < G.vexnum; j++)G.arcs[i][j] = 0;for (int k = 0; k < G.arcnum; k++)//构造邻接矩阵{Vertextype v1, v2;int w;cin >> v1 >> v2;//输入一条边的顶点及边的权值int i = Locatevex(G, v1);int j = Locatevex(G, v2);//确定v1和v2在G中的位置G.arcs[i][j] = 1;//边<v1,v2>的权值置为wG.arcs[j][i] = G.arcs[i][j];//无向图是对称图}return 1;
}
图的深度优先(DFS):
void DFS(AMGraph& G,Vertextype v)
{cout << v<<" ";mp[v] = 1;for (int i = 0; i < G.vexnum; i++){int a = Locatevex(G, v);if (v == G.vexs[i])continue;else{if (G.arcs[a][i] == 1 && !mp[G.vexs[i]])//是邻边且没访问过DFS(G, G.vexs[i]);}}
}
图的打印输出:
void Print(AMGraph G)
{cout << "邻接矩阵:" << endl;for (int i = 0; i < G.vexnum; i++){for (int j = 0; j < G.vexnum; j++)cout << G.arcs[i][j] << " ";cout << endl;}
}
完整代码:
#include<iostream>//无向图邻接矩阵
#include<map>
#define mvnum 100
using namespace std;
typedef char Vertextype;//顶点数据类型
typedef int Arctype;//边权值类型
map<Vertextype, int> mp;
typedef struct
{Vertextype vexs[mvnum];//顶点表Arctype arcs[mvnum][mvnum];//邻接矩阵int vexnum, arcnum;//当前图的点数和边数
}AMGraph;
int Locatevex(AMGraph G, Vertextype u)//在G图中查找顶点u,存在则返回顶点表中的下标,否则返回-1
{for (int i = 0; i < G.vexnum; i++)if (u == G.vexs[i]) return i;return -1;
}
bool Creategraph(AMGraph& G)
{cin >> G.vexnum >> G.arcnum;//输入总顶点数,总边数for (int i = 0; i < G.vexnum; i++){cin >> G.vexs[i];//依次输入点的信息mp[G.vexs[i]]=0;//辅助数组,是否访问过该点,0表示没访问过}for (int i = 0; i < G.vexnum; i++)//初始化邻接矩阵for (int j = 0; j < G.vexnum; j++)G.arcs[i][j] = 0;for (int k = 0; k < G.arcnum; k++)//构造邻接矩阵{Vertextype v1, v2;int w;cin >> v1 >> v2;//输入一条边的顶点及边的权值int i = Locatevex(G, v1);int j = Locatevex(G, v2);//确定v1和v2在G中的位置G.arcs[i][j] = 1;//边<v1,v2>的权值置为wG.arcs[j][i] = G.arcs[i][j];//无向图是对称图}return 1;
}
void DFS(AMGraph& G,Vertextype v)
{cout << v<<" ";mp[v] = 1;for (int i = 0; i < G.vexnum; i++){int a = Locatevex(G, v);if (v == G.vexs[i])continue;else{if (G.arcs[a][i] == 1 && !mp[G.vexs[i]])//是邻边且没访问过DFS(G, G.vexs[i]);}}
}
void Print(AMGraph G)
{cout << "邻接矩阵:" << endl;for (int i = 0; i < G.vexnum; i++){for (int j = 0; j < G.vexnum; j++)cout << G.arcs[i][j] << " ";cout << endl;}
}
int main()
{AMGraph G;Creategraph(G);Print(G);cout << "DFS序列:";DFS(G, 'A');//从A开始遍历
}
测试数据:
| 12 16 A B C D E F G H I J K L A D B C B D B F C F D G E B E F E G E H F I G K H I I K J K K L | 测试数据说明: 1.第一行两个整数分别表示无向图中的顶点数m和边数n; 2.第二行中的m个整数,表示m个顶点数据元素(数据类型为字符型; 3.从第三行开始连续n行数据,每一行两个字符表示无向图中的一条边关联的两个顶点数据信息。 4.无向图如下图示:
|
运行结果:
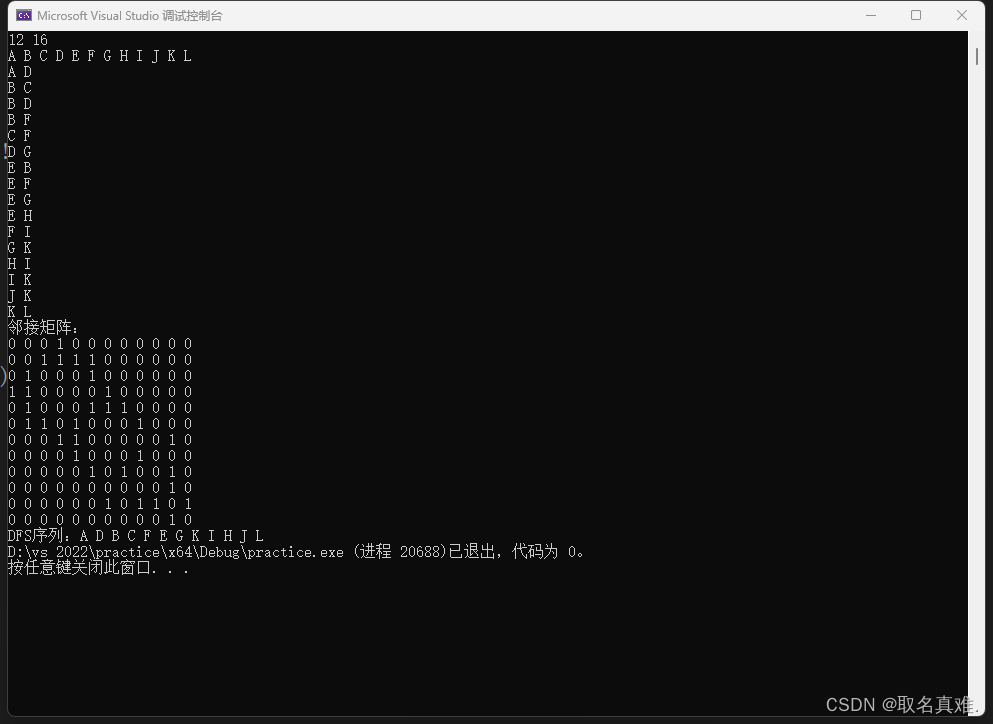
相关文章:

邻接矩阵储存图实现深度优先遍历(C++)
目录 基本要求: 图的结构体: 图的构造: 图的深度优先(DFS): 图的打印输出: 完整代码: 测试数据: 运行结果: 通过给出的图的顶点和边的信息,…...
-42)
hdlbits系列verilog解答(100位加法器)-42
文章目录 一、问题描述二、verilog源码三、仿真结果一、问题描述 通过实例化 100 个完整加法器来创建一个 100 位二进制纹波进位加法器。加法器将两个 100 位数字和一个进位相加,以产生一个 100 位的总和并执行。为了鼓励您实际实例化全加法器,还要在纹波进位加法器中输出每…...

学者观察 | 数字经济中长期发展中的区块链影响力——清华大学柴跃廷
导语 区块链是一种全新的分布式基础架构与计算范式,既能利用非对称加密和冗余分布存储实现信息不可篡改,又可以利用链式数据结构实现数据信息可溯源。当前,区块链技术已成为全球数据交易、金融结算、国际贸易、政务民生等领域的信息基础设施…...

python-flask笔记
服务器图形工具:FinalShellpython虚拟环境用anaconda 标题技术架构和依赖 python3.8 环境 Flask 后端框架 flask-marshmallow webargs 处理参数接收 postgresql 数据库 psycopg2-binary postgresql操作库 Flask-SQLAlchemy orm操作库 flask-admin 超管管理后台 …...

tensor和ndarray的相互转换,同时需要注意cuda和cpu的迁移
从tensor到ndarray:.detach() 方法用于创建一个新的张量,新张量与原始张量共享数据内存,但是不会被计算图追踪。这意味着在新张量上的操作不会影响到原始张量,同时也可以避免梯度传播,适合于提取中间结果。 # 当tenso…...
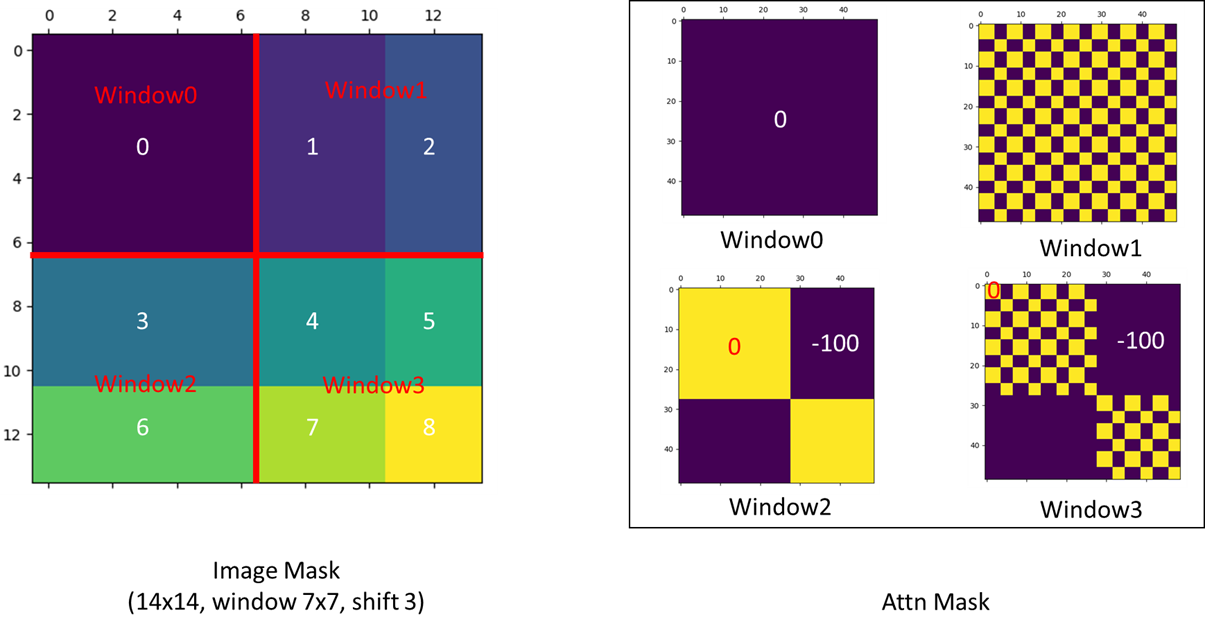
《Swin Transformer: Hierarchical Vision Transformer using Shifted Windows》阅读笔记
论文标题 《Swin Transformer: Hierarchical Vision Transformer using Shifted Windows》 Swin 这个词貌似来自后面的 Shifted WindowsShifted Windows:移动窗口Hierarchical:分层 作者 微软亚洲研究院出品 初读 摘要 提出 Swin Transformer 可以…...
 概念和通用API)
Flink 基础 -- 应用开发(Table API SQL) 概念和通用API
1、概述 Apache Flink提供了两个关系API——Table API和SQL——用于统一的流和批处理。Table API是一个用于Java、Scala和Python的语言集成查询API,它允许以非常直观的方式组合来自关系操作符(如选择、过滤和连接)的查询。Flink的SQL支持基于Apache Calcite&#x…...

Flink之Java Table API的使用
Java Table API的使用 使用Java Table API开发添加依赖创建表环境创建表查询表输出表使用示例 表和流的转换流DataStream转换成表Table表Table转换成流DataStream示例数据类型 自定义函数UDF标量函数表函数聚合函数表聚合函数 API方法汇总基本方法列操作聚合操作Joins合并操作排…...
【Unity细节】Unity中如何让组件失活而不是物体失活
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 😶🌫️收录于专栏:unity细节和bug 😶🌫️优质专栏 ⭐【…...

[设计模式] 建造者模式
一、引言 起因是学习okhttp过程中遇到的这段代码 Request request original.newBuilder().url(original.url()).header("Authorization", "Bearer " BearerTokenUtils.getToken(configuration.getApiKey(), configuration.getApiSecret())).header(&quo…...
)
在DDD领域驱动下的微服务数据库的MVC设计思路(高度可行性)
在DDD领域驱动下的微服务架构中使用MVC设计思路来设计数据库是可行的,因为MVC是一种经典的软件架构模式,可以将应用程序分为三个主要部分:模型、视图和控制器。在微服务架构中,每个微服务可以看作是一个模块,可以使用M…...
Leetcode2834. 找出美丽数组的最小和
Every day a Leetcode 题目来源:2834. 找出美丽数组的最小和 解法1:贪心 从最小正整数 1 开始枚举,设当前数为 num,如果 nums 里没有 target - num,就说明可以添加 num,依次填满直到有 n 个数即可。 用…...

acwing算法基础之搜索与图论--kruskal算法
目录 1 基础知识2 模板3 工程化 1 基础知识 kruskal算法的关键步骤为: 将所有边按照权重从小到大排序。定义集合S,表示生成树。枚举每条边(a,b,c),起点a,终点b,边长c。如果结点a和结点b不连通(用并查集来…...

微信H5跳转微信小程序
官方文档:目录 | 微信开放文档 方法一:微信浏览器打开的h5跳转方式 HTML代码 <wx-open-launch-weapp id"launch-btn" username"所需跳转的小程序原始id" path"pages/pay/pay"><script type"text/wxtag…...

Yii2 引入 外部无命名空间的类,Class not found
记一次问题解决 问题描述 支付宝开放平台SDK v2 无命名空间。需 require 引入。 require Yii::$app->vendorPath."/alipay-sdk-php/v2/aop/AopClient.php"; var_dump(new AopClient([]));exit();上述写法会直接报错。 Class temporary\controllers\AopClient …...

设计模式是测试模式咩?
设计模式和测试模式概述 软件的生命周期为什么要进行测试(测试的目的)?软件的设计模式1. **瀑布模型**3. 增量和迭代模型4. 敏捷模型5. 喷泉模型 测试模型V模型W模型 一个应用程序从出生到“死亡”会经过非常漫长的流程…… 软件的生命周期 …...

Aspose.OCR for .NET 2023Crack
Aspose.OCR for .NET 2023Crack 为.NET在图片上播放OCR使所有用户和程序员都可以从特定的图像片段中提取文本和相关的细节,如字体、设计以及书写位置。这一特定属性为OCR的性能及其在扫描遵循排列的记录时的功能提供了动力。OCR的库使用一条线甚至几条线来处理这些特…...
conda环境中pytorch1.2.0版本安装包安装一直失败解决办法!!!
conda环境中pytorch1.2.0版本安装包安装一直失败解决办法 cuda10.0以及cudnn7.4现在以及安装完成,就差torch的安装了,现在torch我要装的是1.2.0版本的,安装包以及下载好了,安装包都是在这个网站里下载的(点此进入&…...
后端面试问题(学习版)
JAVA相关 JAVA语言概述 1. 一个".java"源文件中是否可以包含多个类?有什么限制? 可以。 一个源文件可以声明多个类,但是最多只能有一个类使用public进行声明 且要求声明public的类的类名与源文件相同。 2. Java的优势ÿ…...

数据管理系统-week1-介绍
文章目录 一、数据它是什么?二、电子存储设备三、持久存储设备1、硬盘驱动器(HDD)、硬盘、硬盘驱动器是一种用于存储和检索数字信息的机电持久存储设备。2、固态硬盘(SSD)使用非易失性存储器,即使用NAND闪存…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

