Leetcode2834. 找出美丽数组的最小和
Every day a Leetcode
题目来源:2834. 找出美丽数组的最小和
解法1:贪心
从最小正整数 1 开始枚举,设当前数为 num,如果 nums 里没有 target - num,就说明可以添加 num,依次填满直到有 n 个数即可。
用集合 nums 存储数据保证唯一性。
代码:
class Solution
{
private:const int MOD = 1e9 + 7;public:int minimumPossibleSum(int n, int target){set<int> nums;nums.insert(1);int num = 2;while (nums.size() < n){if (!nums.count(target - num))nums.insert(num);num++;}return accumulate(nums.begin(), nums.end(), 0LL) % MOD;}
};
结果:
复杂度分析:
时间复杂度:O(n)。
空间复杂度:O(n)。
解法2:数学
我们发现了规律,对于 [1, target−1] 内的数字:
- 1 和 target-1 只能选其中一个,为了使美丽数组的总和最小,我们选1。
- 2 和 target-2 只能选其中一个,为了使美丽数组的总和最小,我们选2。
- …
- 一直到 ⌊target/2⌋,无论 target 是奇数还是偶数,它都可以选。
设 m = min(n, ⌊target/2⌋),我们选择1~m,总和为 m(m+1)/2。
此时还剩下 n-m 个数,只能从 target 开始往后选,一直到 target+n-m-1。
代码:
/** @lc app=leetcode.cn id=2834 lang=cpp** [2834] 找出美丽数组的最小和*/// @lc code=start
// class Solution
// {
// private:
// const int MOD = 1e9 + 7;// public:
// int minimumPossibleSum(int n, int target)
// {
// set<int> nums;
// nums.insert(1);
// int num = 2;
// while (nums.size() < n)
// {
// if (!nums.count(target - num))
// nums.insert(num);
// num++;
// }
// return accumulate(nums.begin(), nums.end(), 0LL) % MOD;
// }
// };class Solution
{
private:const int MOD = 1e9 + 7;public:int minimumPossibleSum(int n, int target){long long m = min(target / 2, n);return (cal(1, m) + cal(target, target + n - m - 1)) % MOD;}// 辅函数 - 返回 [left, right] 区间内元素和long long cal(int left, int right){long long sum = 0;for (int i = left; i <= right; i++)sum += i;return sum;}
};
// @lc code=end
结果:
复杂度分析:
时间复杂度:O(1)。
空间复杂度:O(1)。
相关文章:

Leetcode2834. 找出美丽数组的最小和
Every day a Leetcode 题目来源:2834. 找出美丽数组的最小和 解法1:贪心 从最小正整数 1 开始枚举,设当前数为 num,如果 nums 里没有 target - num,就说明可以添加 num,依次填满直到有 n 个数即可。 用…...

acwing算法基础之搜索与图论--kruskal算法
目录 1 基础知识2 模板3 工程化 1 基础知识 kruskal算法的关键步骤为: 将所有边按照权重从小到大排序。定义集合S,表示生成树。枚举每条边(a,b,c),起点a,终点b,边长c。如果结点a和结点b不连通(用并查集来…...

微信H5跳转微信小程序
官方文档:目录 | 微信开放文档 方法一:微信浏览器打开的h5跳转方式 HTML代码 <wx-open-launch-weapp id"launch-btn" username"所需跳转的小程序原始id" path"pages/pay/pay"><script type"text/wxtag…...

Yii2 引入 外部无命名空间的类,Class not found
记一次问题解决 问题描述 支付宝开放平台SDK v2 无命名空间。需 require 引入。 require Yii::$app->vendorPath."/alipay-sdk-php/v2/aop/AopClient.php"; var_dump(new AopClient([]));exit();上述写法会直接报错。 Class temporary\controllers\AopClient …...

设计模式是测试模式咩?
设计模式和测试模式概述 软件的生命周期为什么要进行测试(测试的目的)?软件的设计模式1. **瀑布模型**3. 增量和迭代模型4. 敏捷模型5. 喷泉模型 测试模型V模型W模型 一个应用程序从出生到“死亡”会经过非常漫长的流程…… 软件的生命周期 …...

Aspose.OCR for .NET 2023Crack
Aspose.OCR for .NET 2023Crack 为.NET在图片上播放OCR使所有用户和程序员都可以从特定的图像片段中提取文本和相关的细节,如字体、设计以及书写位置。这一特定属性为OCR的性能及其在扫描遵循排列的记录时的功能提供了动力。OCR的库使用一条线甚至几条线来处理这些特…...
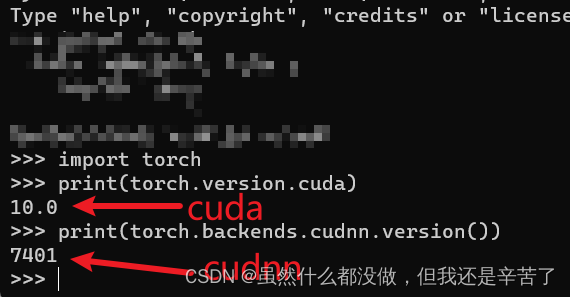
conda环境中pytorch1.2.0版本安装包安装一直失败解决办法!!!
conda环境中pytorch1.2.0版本安装包安装一直失败解决办法 cuda10.0以及cudnn7.4现在以及安装完成,就差torch的安装了,现在torch我要装的是1.2.0版本的,安装包以及下载好了,安装包都是在这个网站里下载的(点此进入&…...
后端面试问题(学习版)
JAVA相关 JAVA语言概述 1. 一个".java"源文件中是否可以包含多个类?有什么限制? 可以。 一个源文件可以声明多个类,但是最多只能有一个类使用public进行声明 且要求声明public的类的类名与源文件相同。 2. Java的优势ÿ…...

数据管理系统-week1-介绍
文章目录 一、数据它是什么?二、电子存储设备三、持久存储设备1、硬盘驱动器(HDD)、硬盘、硬盘驱动器是一种用于存储和检索数字信息的机电持久存储设备。2、固态硬盘(SSD)使用非易失性存储器,即使用NAND闪存…...

【SpringBoot】手写模拟SpringBoot核心流程
依赖包 新建一个工程,包含两个 module: springboot 模块,表示 springboot 源码实现;user 模块,表示业务系统,使用 springboot 模块; 依赖包:Spring、SpringMVC、Tomcat 等ÿ…...

应对.locked勒索病毒:恢复、预防全方位攻略
导言: .locked勒索病毒并非简单的数字威胁,它是一场对个人和企业数字资产的精密审判。这种病毒通过各种方式感染系统,从而以瞬间之间将用户的关键文件变成数字拼图,无情地要求赎金以换取解锁的密钥。如果您正在经历勒索病毒数据恢…...

基于DS1302时钟液晶12864显示2路闹钟仿真及源程序
一、系统方案 1、本设计采用51单片机作为主控器。 2、DS1302采集年月日时分秒送到液晶12864显示。 3、按键年月日时分秒,两路闹钟。 二、硬件设计 原理图如下: 三、单片机软件设计 1、首先是系统初始化 uchar clock_time[6] {0X00,0X59,0X23,0X09,0X…...

AGC034E Complete Compress
AGC034E Complete Compress 洛谷[AGC034E] Complete Compress 题目大意 给你一棵有 n n n个节点的树,并用 01 01 01串告诉你哪些节点上有棋子(恰好一棵)。 你可以进行若干次操作,每次操作可以将两颗距离至少为 2 2 2的棋子向彼…...

python设计模式12:状态模式
什么是状态机? 关键属性: 状态和转换 状态: 系统当前状态 转换:一种状态到另外一种状态的变化。 转换由触发事件或是条件启动。 状态机-状态图 状态机使用场景: 自动售货机 电梯 交通灯 组合锁 停车计时…...
)
JS对图片尺寸和DPI进行编辑修改(1寸照修改为2寸照)
各种报名都对照片有大小限制,鉴于这种情况,网上搜了后拼凑出了如下代码,用于解决1寸照片修改为2寸照片,同时将DPI修改为300,当然也可以根据自己的情况修改代码: HTML <input type"file" id&…...

EDA实验----四选一多路选择器设计(QuartusII)
目录 一.实验目的 二.实验仪器设备 三.实验原理: 四.实验要求 五.实验内容及步骤 1.实验内容 2.实验步骤 六.实验报告 七.实验过程 1.创建Verilog文件,写代码 2.波形仿真 …...

从windows iso文件中提取install.wim
1、首先从微软官方下载需要的windows镜像 https://www.microsoft.com/zh-cn/software-download/windows10/ 2、在下载的iso文件右键,打开压缩包,在sources文件夹下,应该就可以看到install.wim了。但似乎在最新的win10版本,微软采…...

Python的flask网页编程的GET和POST方法的区别
关于flask网页编程的GET及POST方法之间存在哪些区别问题,我们主要从以下六个关键点予以详细阐述: 首先需要明确的是,GET与POST两种不同类型的HTTP方法所采用的请求模式有所差别。其中,GET方法采用的是基于URL请求的机制ÿ…...
15 # 手写 throttle 节流方法
什么是节流 节流是限制事件触发的频率,当持续触发事件时,在一定时间内只执行一次事件,这个效果跟英雄联盟里的闪现技能释放差不多。 函数防抖关注一定时间连续触发的事件只在最后执行一次,而函数节流侧重于一段时间内只执行一次…...

puzzle(1612)拼单词、wordlegame
目录 拼单词 wordlegame 拼单词 在线play 找出尽可能多的单词。 如果相邻的话(在任何方向上),你可以拖拽鼠标从一个字母(方格)到另一个字母(方格)。在一个单词中,你不能多次使用…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
