2023NOIP A层联测28-小猫吃火龙果
给你一个长为 n n n 的序列,每个位置是 A , B , C A,B,C A,B,C 三个中的一个物品。
A A A 吃 B B B, B B B 吃 C C C, C C C 吃 A A A。
现在有 m m m 次操作,每次操作有两种:
-
区间修改:给出 l , r , x , y l,r,x,y l,r,x,y,表示将 [ l , r ] [l,r] [l,r] 区间内所有的 x x x 改成 y y y,所有的 y y y 改成 x x x(两种修改同时进行)。
-
区间询问:给出 l , r , x l,r,x l,r,x,现在沙奈朵一开始手上拿着的是一个 x x x 物品。沙奈朵从序列的 l l l 位置开始一路走到 r r r 位置结束,每次他需要对比他手上的物品和当前序列位置的物品,如果手上的物品可以吃掉当前序列位置的物品,则手上的物品不变,否则手上的物品变成当前序列位置的物品。区间询问操作对序列没有任何修改。 求走完了 [ l , r ] [l,r] [l,r] 这个区间后,沙奈朵手上的物品是什么。对区间 [ l , r ] [l,r] [l,r] 中的每一个位置,包括端点,都需要执行操作。
n , m ≤ 2 × 1 0 5 n,m\le2\times10^5 n,m≤2×105
考虑用分块维护。由于有交换两种字母的操作,那么对于每个就要维护三个字母所有置换( 6 6 6 种)。将 A B C , A C B , B A C , B C A , C A B , C B A ABC,ACB,BAC,BCA,CAB,CBA ABC,ACB,BAC,BCA,CAB,CBA 分别表示为 0 , 1 , 2 , 3 , 4 , 5 0,1,2,3,4,5 0,1,2,3,4,5;将修改操作交换 A B , A C , B C AB,AC,BC AB,AC,BC 分别表示为 0 , 1 , 2 0,1,2 0,1,2;记块长为 B B B
设
c x , y c_{x,y} cx,y 表示字母是 y y y,经过置换 x x x 会变成的字母。
b x , y b_{x,y} bx,y 表示经过修改 y y y 后,置换 x x x 会变成的置换。
t o i d , x , y to_{id,x,y} toid,x,y 表示第 i d id id 个块置换为 x x x,开始是字母 y y y,走完这个块后所变成的字母。
t i d t_{id} tid 表示第 i d id id 个块的置换。
显然 c , b c,b c,b 可以打表, t o to to 可以 O ( B ) O(B) O(B) 求出。
下面考虑维护。
- 修改。对于散块先更新所在的块的真实值,然后直接修改,再 O ( B ) O(B) O(B) 求出 t o i d to_{id} toid;对于整块就用 b b b 更改 t i d t_{id} tid 即可。
- 查询。对于散块就直接暴力比对;对于整块就用之前求出的 t o to to 更新答案。
时间复杂度 O ( n n ) O(n\sqrt n) O(nn),但是由于修改时对于散块的求 t o to to 的时间复杂度实际上要带上 18 18 18 的常数,所以块长取 ⌈ n 18 ⌉ \sqrt{\lceil\frac n{18}\rceil} ⌈18n⌉ 比较合适。
具体实现参照代码:
#include<bits/stdc++.h>
#define getnxt(now,x) (now==(x+1)%3?x:now)
using namespace std;
const int N=2e5+1;
int n,m,block,to[2000][6][3],t[2000];
int c[6][3]={{0,1,2},{0,2,1},{1,0,2},{1,2,0},{2,0,1},{2,1,0}};
int b[6][3]={{2,5,1},{3,4,0},{0,3,4},{1,2,5},{5,1,2},{4,0,3}};
char a[N];
void renew(int id)
{int l=id*block+1,r=min(id*block+block,n);for(int i=l;i<=r;i++) a[i]=c[t[id]][a[i]-65]+65;t[id]=0;
}
void update(int id)
{int l=id*block+1,r=min(id*block+block,n);for(int x=0;x<6;x++){for(int y=0;y<3;y++){to[id][x][y]=y;for(int i=l;i<=r;i++){to[id][x][y]=getnxt(to[id][x][y],c[x][a[i]-65]);}}}
}
int main()
{freopen("training.in","r",stdin);freopen("training.out","w",stdout);cin.tie(0)->sync_with_stdio(0);cin>>n>>m>>(a+1);block=sqrt((n+17)/18);for(int i=0;i<=(n+block-1)/block;i++) update(i);for(int i=1,op,l,r;i<=m;i++){char x,y;cin>>op>>l>>r>>x;if(op){int minr=min((l-1)/block*block+block,r),id=(l-1)/block;x-=65;while(l<=minr){x=getnxt(x,c[t[id]][a[l]-65]);l++;}while(r-l+1>=block){id=(l-1)/block;x=to[id][t[id]][x];l+=block;}id=(l-1)/block;while(l<=r){x=getnxt(x,c[t[id]][a[l]-65]);l++;}cout<<char(x+65)<<"\n";}else{cin>>y;if(x==y) continue;if(x>y) swap(x,y);int type=(x=='A'?y=='B'?0:1:2);int minr=min((l-1)/block*block+block,r),id=(l-1)/block;renew(id);while(l<=minr){if(a[l]==x) a[l]=y;else if(a[l]==y) a[l]=x;l++;}update(id);while(r-l+1>=block){t[(l-1)/block]=b[t[(l-1)/block]][type];l+=block;}renew(id=(l-1)/block);while(l<=r){if(a[l]==x) a[l]=y;else if(a[l]==y) a[l]=x;l++;}update(id);}}
}
相关文章:

2023NOIP A层联测28-小猫吃火龙果
给你一个长为 n n n 的序列,每个位置是 A , B , C A,B,C A,B,C 三个中的一个物品。 A A A 吃 B B B, B B B 吃 C C C, C C C 吃 A A A。 现在有 m m m 次操作,每次操作有两种: 区间修改:给出 l , r…...

C# Dictionary与List的用法区别与联系
C#是一门广泛应用于软件开发的编程语言,其中Dictionary和List是两种常用的集合类型。它们在存储和操作数据时有着不同的特点和用途。本文将详细探讨C# Dictionary和List的用法区别与联系,并通过代码示例进行对比,以帮助读者更好地选择适合自己…...

Git应用(1)
一、Git Git(读音为/gɪt/。中文 饭桶 )是一个开源的分布式版本控制系统,可以有效、高速地处理从很小到非常大的项目版本管理。 了解更多可到GIT官网:Git - Downloads GIT一般工作流程如下: 1.从远程仓库中克隆 Git 资源作为本地…...

【Java】Netty创建网络服务端客户端(TCP/UDP)
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍Netty创建网络服务端客户端示例。 学其所用,用其所学。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下次更…...

Android 设计模式--单例模式
一,定义 单例模式就是确保某一个类只有一个实例,而且自行实例化,并向整个系统提供这个实例 二,使用场景 确保某个类只有一个对象的使用场景,避免产生多个对象消耗过多的资源,或者某种类型的对象只应该有…...

语音识别与自然语言处理(NLP):技术前沿与未来趋势
语音识别与自然语言处理(NLP):技术前沿与未来趋势 随着科技的快速发展,语音识别与自然语言处理(NLP)技术逐渐成为人工智能领域的研究热点。这两项技术的结合,使得机器能够更好地理解和处理人类语…...
k8s-docker二进制(1.28)的搭建
二进制文件-docker方式 1、准备的服务器 角色ip组件k8s-master1192.168.11.111kube-apiserver,kube-controller-manager,kube-scheduler,etcdk8s-master2192.168.11.112kube-apiserver,kube-controller-manager,kube-scheduler,etcdk8s-node1192.168.11.113kubelet,kube-prox…...
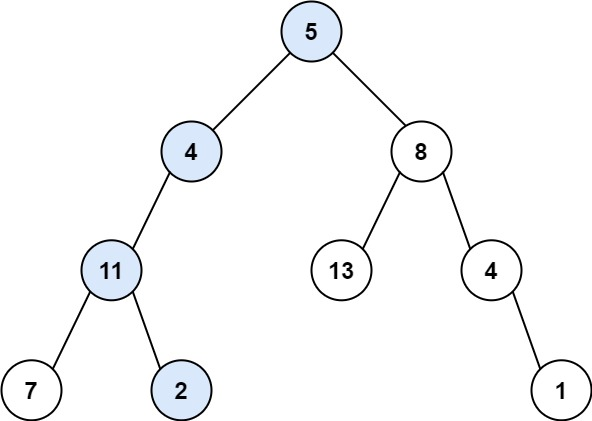
【代码随想录】算法训练计划18
1、513. 找树左下角的值 题目: 给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。 假设二叉树中至少有一个节点。 思路: 递归,规则,基本可以自己写出来 var maxDepth int var res int fun…...
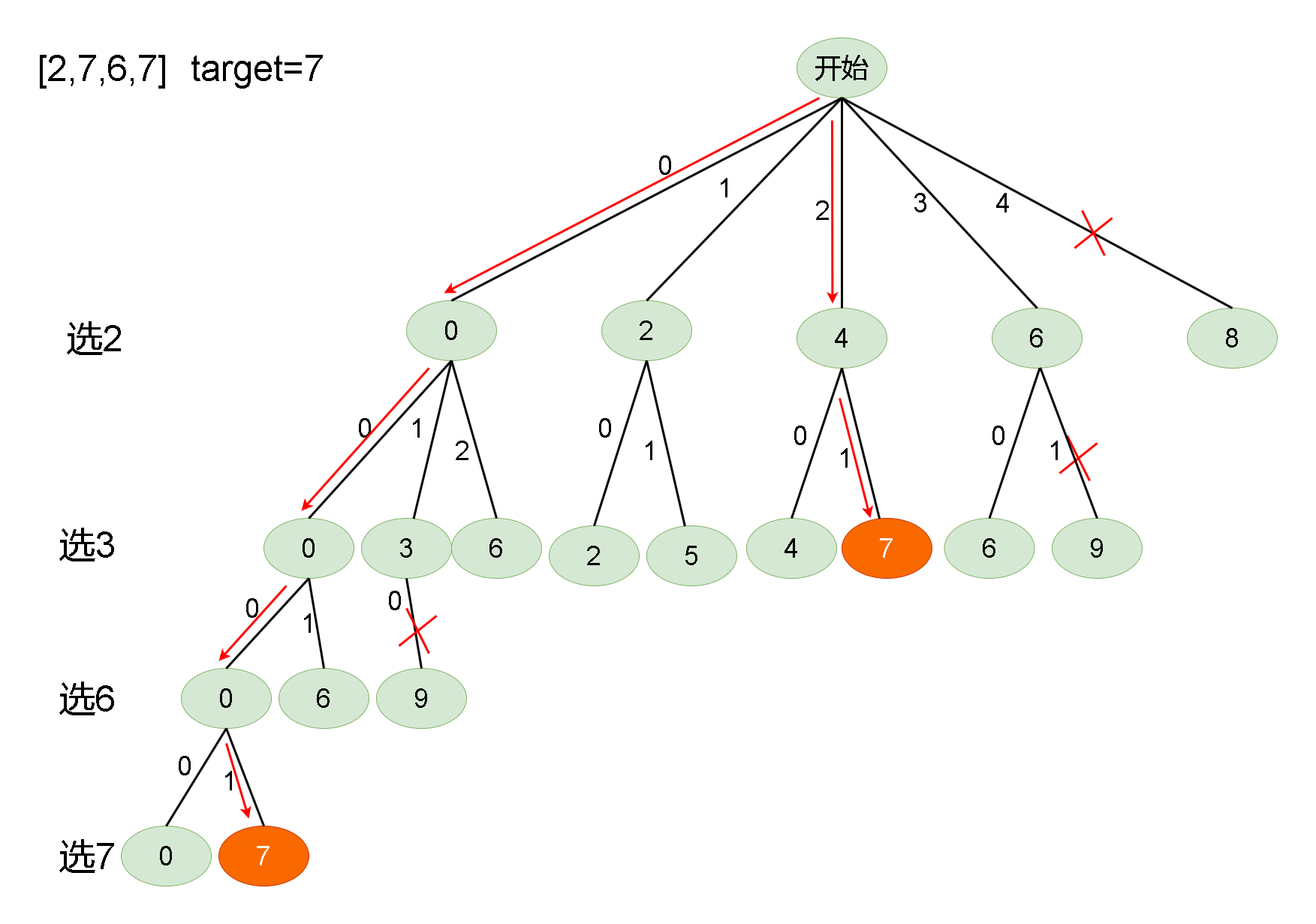
Leetcode刷题详解—— 组合总和
1. 题目链接:39. 组合总和 2. 题目描述: 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些…...
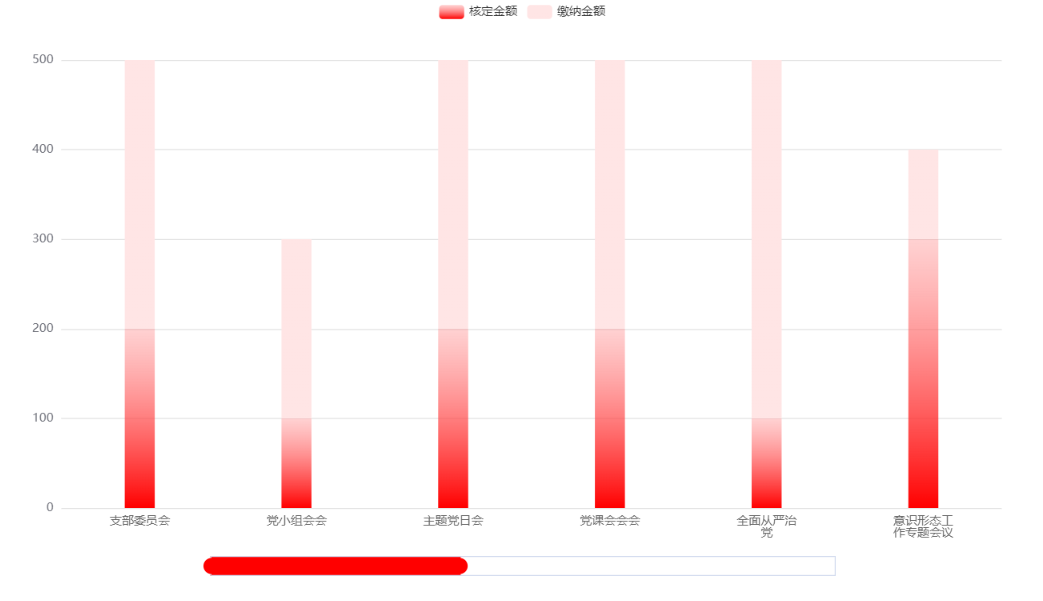
Echarts柱状体实现滚动条动态滚动
当我们柱状图中X轴数据太多的时候,会自动把柱形的宽度挤的很细,带来的交互非常不好,因此就有一个属性来解决:dataZoom 第一种简易的版本,横向滚动。 dataZoom: {show: true, // 为true 滚动条出现realtime: true, // 实…...

SplayTree高分测试用例
测试用例结果展示 覆盖率 变异得分 测试注意点 从SplayTree测起,然后再测SubSplayTree,因为前者调用后者。SplaySubTree的remove方法大部分内容需要通过反射才能测到。value和index在SplayTree当中都不是唯一的。一个index可能对应多个value。 不足之…...

制作麒麟V10-server-sp2镜像
1.挂载iso 文件到目录 mount -o loop /xxx.iso /mnt 这样mnt 目录下会有iso 解压相关的文件 2.修改源文件内容 vim /etc/yum.repos.d/ kylin_x86_64.repo 将里面的所有的源enabled 都改成 0 并添加一个新的源 [ks10-local] name Kylin Linux Advanced Server 10 - Local base…...
2.docker镜像的导入导出
目录 概述docker 常用命令下载导出导入镜像结束 概述 docker 常用命令 本章节使用到的命令,总结在此,后面有使用案例。 命令作用docker images显示镜像docker rmi $(docker images -q)删除系统上所有的镜像docker rmi -f强制删除多个镜像 :…...

bs4介绍和遍历文档树、搜索文档树、案例:爬美女图片、 bs4其它用法、css选择器
bs4介绍和遍历文档树 BeautifulSoup 是一个可以从HTML或XML文件中提取数据的Python库,解析库 需要安装模块:pip install beautifulsoup4 使用 解析库可以使用 lxml,速度快(必须安装) 可以使用python内置的 # html…...
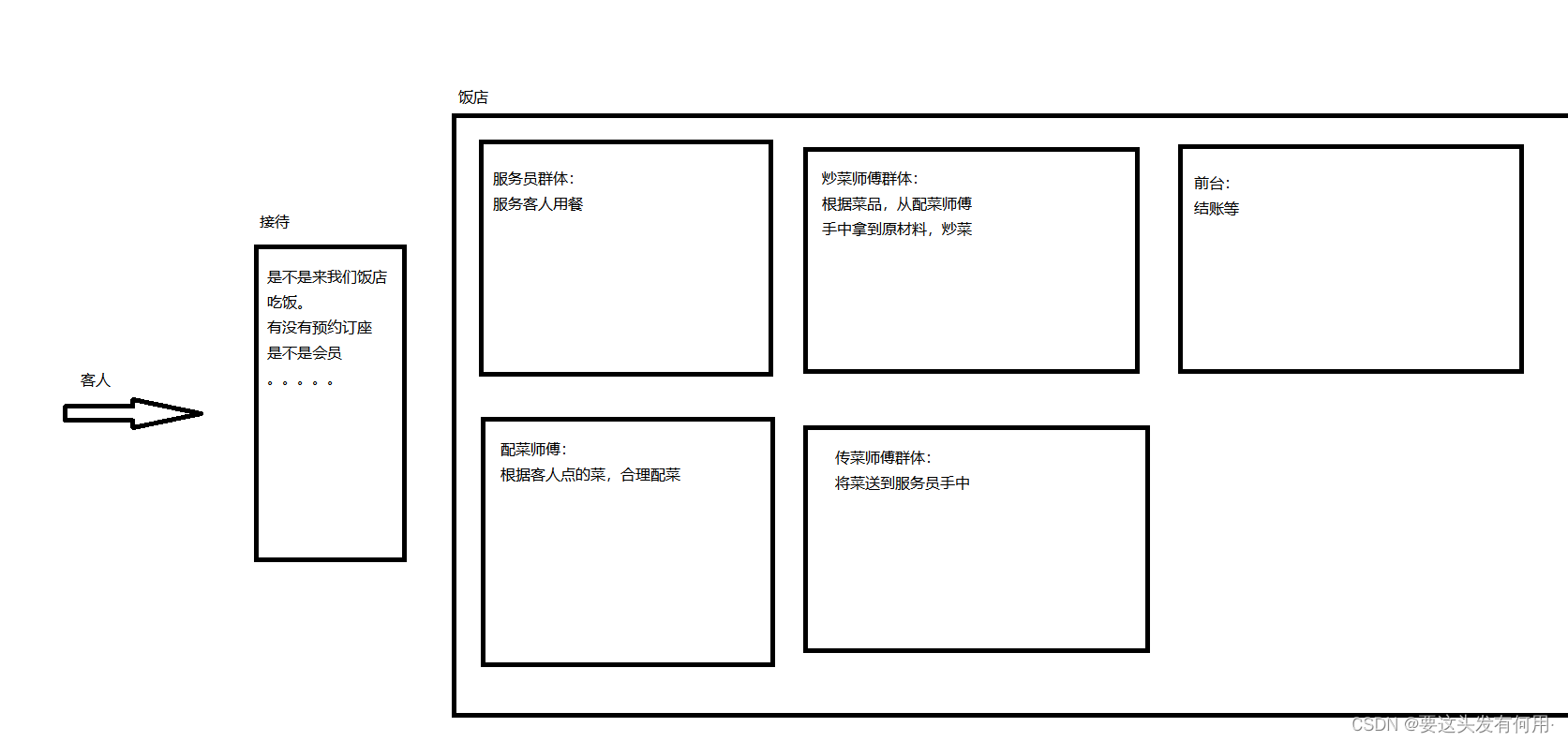
微服务-开篇-个人对微服务的理解
从吃饭说起 个人理解新事物的时候喜欢将天上飞的理念转换成平常生活中的实践,对比理解这些高大上的名词,才能让我们减少恐慌的同时加深理解。废话不多说,我们从吃饭开始说起,逐渐类比出微服务的思想。 (个人见解&…...

机器学习算法-集成学习
概念 集成学习是一种机器学习方法,它通过构建并结合多个机器学习器(基学习器)来完成学习任务。集成学习的潜在思想是即便某一个弱分类器得到了错误的预测,其他的弱分类器也可以将错误纠正回来。集成学习通常被视为一种元算法&…...

LINUX入门篇【4】开发篇--开发工具vim的使用
前言: 从这一篇开始,我们将正式进入使用LINUX进行写程序和开发的阶段,可以说,由此开始,我们才开始真正去使用LINUX。 介绍工具: 1.LINUX软件包管理器yum: 1.yum的介绍: 在LINUX…...

代码随想录算法训练营Day 50 || 309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费
309.最佳买卖股票时机含冷冻期 力扣题目链接 给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。 设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票): 你不能同时…...

【C语言】【数据结构】【环形链表判断是否带环并返回进环节点】有数学推导加图解
1.判断是否带环: 用快慢指针 slow指针一次走一步,fast指针一次走两步 当两个指针相遇时,链表带环;两个指针不能相遇时,当fast走到倒数第一个节点或为空时,跳出循环返回空指针。 那么slow指针一次走一步&a…...
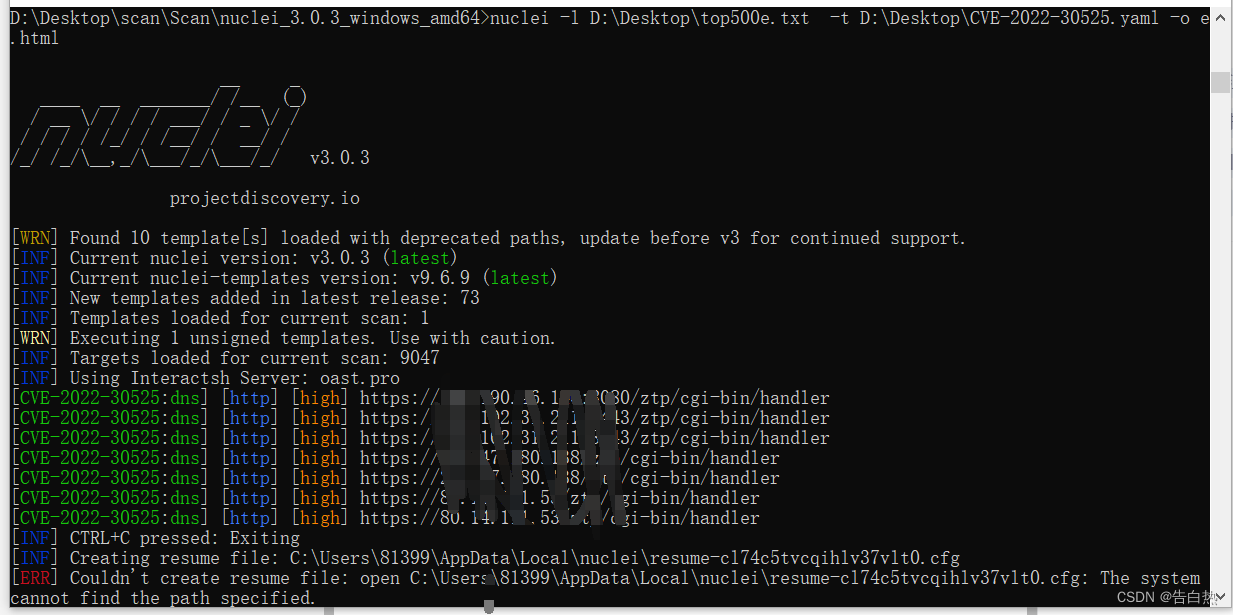
漏洞扫描-nuclei-poc编写
0x00 nuclei Nuclei是一款基于YAML语法模板的开发的定制化快速漏洞扫描器。它使用Go语言开发,具有很强的可配置性、可扩展性和易用性。 提供TCP、DNS、HTTP、FILE 等各类协议的扫描,通过强大且灵活的模板,可以使用Nuclei模拟各种安全检查。 …...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...
