平面运动机器人的传感器外参标定
简述
对任意两个传感器进行外参标定可以采用手眼标定算法来完成,但是,传统手眼标定算法对于运动具有一定的要求,可以证明,至少需要两个以上轴角方向不同的旋转运动才可以正确估计出外参旋转,因此,如果使用手眼标定算法标定外参,例如标定imu与激光雷达、imu与相机、多激光雷达的外参… 那么需要充分的全方位空间的旋转和平移运动,才可以成功完成标定。
但是如果机器人是处于平面运动的地面机器人呢?那么这个时候很可能很多的外参都是不可观的,准确来说,依然存在一个特殊情况,使得我们可以使用特定的算法标定出除了z轴平移外的全部参数,即其中一个传感器旋转运动时的轴角方向和它的z轴刚好平行,除此之外,也就是说如果你的传感器安装角度不满足这个条件,那么就别指望仅靠平面上运动就能完成标定。
简单来说,对于平面运动机器人的传感器外参标定,有两个结论:
1、如果其中一个传感器的旋转运动的轴角方向与其传感器坐标z轴是平行的,那么可以标定出除了z轴平移外的全部参数。
2、任意安装的两个传感器在平面运动下外参不可观。
例如,平面运动机器人中,轮速计、2d激光雷达等和车体平行安装的传感器都满足结论一的条件。下面将介绍如何通过算法求解出外参。
算法
分为两个步骤 1、先求解出旋转的pitch和roll。2、求解yaw、x,y。
step1:
首先我们知道手眼标定的旋转关系:
q R i R i + 1 ⊗ q R C = q R C ⊗ q C i C i + 1 q^{R_{i+1}} _{R_i}\otimes q^C_R=q^C_R \otimes q^{C_{i+1}}_{C_i} qRiRi+1⊗qRC=qRC⊗qCiCi+1其中R表示任何与车体水平安装的传感器(例如轮速计、2D激光…),C表示任意其他3D传感器如相机、3D激光雷达… 外参旋转为 q R C q^C_R qRC。
注意符号 q b a q^a_b qba表示a->b的旋转,即 q b a q_{ba} qba。
由上式得:
q R i R i + 1 ⊗ q R C − q R C ⊗ q C i C i + 1 = 0 = > ( Q L ( q R i R i + 1 ) − Q R ( q C i C i + 1 ) ) q R C = 0 (1) q^{R_{i+1}}_{R_i}\otimes q^C_R-q^C_R \otimes q^{C_{i+1}}_{C_i}=0 \\ =>\begin{aligned} (Q_L(q^{R_{i+1}}_{R_i})-Q_R(q^{C_{i+1}}_{C_i}))q^C_R=0 \end{aligned}\tag{1} qRiRi+1⊗qRC−qRC⊗qCiCi+1=0=>(QL(qRiRi+1)−QR(qCiCi+1))qRC=0(1)
Q L , Q R Q_L,Q_R QL,QR即四元数的左乘、右乘矩阵。
因此转换为了一个齐次线性方程组,在给定约束 ∣ ∣ q R C ∣ ∣ = 1 ||q^C_R||=1 ∣∣qRC∣∣=1下求解该方程的最小二乘解即可解得 q R C q^C_R qRC。
但是由于我们的运动被限制为平面运动,上面方程的秩为2,存在多余的零空间维度,因此无法正确求解,因此我们采用别的技巧进行处理,首先将外参旋转表示为z-y-z 欧拉角形式:
q R C = q z ( α ) q y ( β ) q z ( γ ) (2) \begin{aligned} q^C_R=q_z(\alpha)q_y(\beta)q_z(\gamma)\end{aligned}\tag{2} qRC=qz(α)qy(β)qz(γ)(2) q z ( α ) q_z(\alpha) qz(α)即绕z轴旋转 α \alpha α角度 , q y ( β ) q_y(\beta) qy(β)为绕y轴旋转 β \beta β角度。
根据轴角到四元数的转换关系 q = [ c o s α 2 , u s i n α 2 ] q=[cos\frac{\alpha}{2},usin\frac{\alpha}{2}] q=[cos2α,usin2α],可得:
q z ( α ) = [ c o s α 2 , 0 , 0 , s i n α 2 ] T q_z(\alpha)=[cos\frac{\alpha}{2},0,0,sin\frac{\alpha}{2}]^T qz(α)=[cos2α,0,0,sin2α]T q y ( β ) = [ c o s β 2 , 0 , s i n β 2 , 0 ] T q_y(\beta)=[cos\frac{\beta}{2},0,sin\frac{\beta}{2},0]^T qy(β)=[cos2β,0,sin2β,0]T
将(2)带入(1)可得:
q R i R i + 1 ⊗ q z ( α ) q y ( β ) q z ( γ ) − q z ( α ) q y ( β ) q z ( γ ) ⊗ q C i C i + 1 = 0 q^{R_{i+1}}_{R_i}\otimes q_z(\alpha)q_y(\beta)q_z(\gamma)\\-q_z(\alpha)q_y(\beta)q_z(\gamma)\otimes q^{C_{i+1}}_{C_i}=0 qRiRi+1⊗qz(α)qy(β)qz(γ)−qz(α)qy(β)qz(γ)⊗qCiCi+1=0关键来了,由于传感器R的旋转轴与z轴平行,因此可将 q R i R i + 1 q^{R_{i+1}}_{R_i} qRiRi+1和 q z ( α ) q_z(\alpha) qz(α)的顺序交换,可得下式:
δ = q z ( α ) ⊗ q R i R i + 1 q y ( β ) q z ( γ ) − q z ( α ) q y ( β ) q z ( γ ) ⊗ q C i C i + 1 = q z ( α ) ( q R i R i + 1 q y ( β ) q z ( γ ) − q y ( β ) q z ( γ ) q C i C i + 1 ) \delta =q_z(\alpha) \otimes q^{R_{i+1}}_{R_i} q_y(\beta)q_z(\gamma)\\-q_z(\alpha)q_y(\beta)q_z(\gamma)\otimes q^{C_{i+1}}_{C_i}\\=q_z(\alpha)(q^{R_{i+1}}_{R_i} q_y(\beta)q_z(\gamma)-q_y(\beta)q_z(\gamma)q^{C_{i+1}}_{C_i}) δ=qz(α)⊗qRiRi+1qy(β)qz(γ)−qz(α)qy(β)qz(γ)⊗qCiCi+1=qz(α)(qRiRi+1qy(β)qz(γ)−qy(β)qz(γ)qCiCi+1)
显然,
q R i R i + 1 q y ( β ) q z ( γ ) − q y ( β ) q z ( γ ) q C i C i + 1 = 0 q^{R_{i+1}}_{R_i} q_y(\beta)q_z(\gamma)-q_y(\beta)q_z(\gamma)q^{C_{i+1}}_{C_i}=0 qRiRi+1qy(β)qz(γ)−qy(β)qz(γ)qCiCi+1=0
将 q y ( β ) q z ( γ ) q_y(\beta)q_z(\gamma) qy(β)qz(γ)记为 q Y Z q_{YZ} qYZ,
q Y Z = [ c o s ( β 2 ) c o s ( γ 2 ) s i n ( β 2 ) s i n ( γ 2 ) s i n ( β 2 ) c o s ( γ 2 ) c o s ( β 2 ) s i n ( γ 2 ) ] (3) \begin{aligned} q_{YZ}=\begin{bmatrix} cos(\frac{\beta}{2})cos(\frac{\gamma}{2})\\sin(\frac{\beta}{2})sin(\frac{\gamma}{2}) \\ sin(\frac{\beta}{2})cos(\frac{\gamma}{2})\\cos(\frac{\beta}{2})sin(\frac{\gamma}{2})\end{bmatrix}\end{aligned} \tag{3} qYZ= cos(2β)cos(2γ)sin(2β)sin(2γ)sin(2β)cos(2γ)cos(2β)sin(2γ) (3)
于是,这个问题转换为一个求解 q Y Z q_{YZ} qYZ的最小二乘问题:
q Y Z = arg min q Y Z ∣ ∣ M q Y Z ∣ ∣ 2 M = [ L ( q R i R i + 1 ) − R ( q C i C i + 1 ) . . L ( q R 0 R 1 ) − R ( q C 0 C 1 ) ] q_{YZ}=\argmin \limits_{q_{YZ}}||Mq_{YZ}||^2\\ M=\begin{bmatrix} L(q^{R_{i+1}}_{R_i})-R(q^{C_{i+1}}_{C_i}) \\ .\\.\\L(q^{R_{1}}_{R_0})-R(q^{C_{1}}_{C_0})\end{bmatrix} qYZ=qYZargmin∣∣MqYZ∣∣2M= L(qRiRi+1)−R(qCiCi+1)..L(qR0R1)−R(qC0C1)
可以证明,这个矩阵M的秩为2,证明过程见文献【2】,因此,上述最小二乘解的零空间维度为2,因此我们需要继续寻找约束,根据(3)式可知: q Y Z 1 q Y Z 2 = q Y Z 3 q Y Z 4 q_{YZ1}q_{YZ2}=q_{YZ3}q_{YZ4} qYZ1qYZ2=qYZ3qYZ4另外表示旋转的四元数都是单位四元数: ∣ ∣ q Y Z ∣ ∣ 2 = 1 ||q_{YZ}||_2=1 ∣∣qYZ∣∣2=1对于上述齐次线性最小二乘问题,其解为 M T M M^TM MTM最小特征值对应的特征向量,因为M的秩为2,因此有两个为0的最小特征值,这两个0特征值对应的两个线性无关的特征向量记为 t 1 , t 2 t_1,t_2 t1,t2,它们构成了零空间的一组基(实对称矩阵必能对角化,有n个相同的特征值必然存在n个不相关的特征向量),因此解可以表示为: q Y Z = a t 1 + b t 2 q_{YZ}=at_1+bt_2 qYZ=at1+bt2根据上面给出的两个约束即可以求解出 a , b a,b a,b。
需要注意的是,由于噪声影响, M T M M^TM MTM最终是满秩的,并不会有两个真正为0的特征值,因此只需要取2个最小的特征值对应的特征向量即可。
step2求解yaw,x,y
根据手眼标定,有关系:
( R ( q R i R i + 1 ) − I ) p R C − R Z ( α ) R ( q Y Z ) p C i C i + 1 + p R i R i + 1 = 0 (R(q^{R_{i+1}}_{R_i})-I)p^C_R-R_Z(\alpha)R(q_{YZ})p^{C_{i+1}}_{C_i}+p^{R_{i+1}}_{R_i}=0 (R(qRiRi+1)−I)pRC−RZ(α)R(qYZ)pCiCi+1+pRiRi+1=0其中, q Y Z q_{YZ} qYZ即step1求解的结果, R Z ( α ) R_Z(\alpha) RZ(α)即外参旋转待求的一部分, p R C p^C_R pRC为待求外参平移。
由于外参平移中,z发生变化时传感器的运动观测保持不变 ,因此z方向的平移是不可观的,因此将外参平移z设为0,并丢弃上式第3行,
R ( q Y Z ) p C i C i + 1 R(q_{YZ})p^{C_{i+1}}_{C_i} R(qYZ)pCiCi+1即将传感器C的运动投影到运动平面,令: R ( q Y Z ) p C i C i + 1 = [ p i 1 p i 2 p i 3 ] R(q_{YZ})p^{C_{i+1}}_{C_i}=\begin{bmatrix}p_{i_1}\\p_{i_2}\\p_{i_3}\end{bmatrix} R(qYZ)pCiCi+1= pi1pi2pi3
带入上式并忽略第3行,可得: ( R ( q R i R i + 1 ) − I ) 2 × 2 [ p x p y ] − [ c o s α − s i n α s i n α c o s α ] [ p i 1 p i 2 ] + p R i R i + 1 = 0 (R(q^{R_{i+1}}_{R_i})-I)_{2\times2}\begin{bmatrix}p_x\\p_y\end{bmatrix}-\\\begin{bmatrix}cos\alpha&-sin\alpha \\ sin\alpha & cos\alpha \end{bmatrix}\begin{bmatrix} p_{i_1}\\ p_{i_2}\end{bmatrix}+p^{R_{i+1}}_{R_i}=0 (R(qRiRi+1)−I)2×2[pxpy]−[cosαsinα−sinαcosα][pi1pi2]+pRiRi+1=0
使用最小二乘法即可解得 p x , p y , α p_x,p_y,\alpha px,py,α,具体细节见参考文献【2】。
reference:
[1] 标定系列一 | 机器人手眼标定的基础理论分析 https://zhuanlan.zhihu.com/p/93183788?utm_psn=1706381723099791360
[2] An Analytical Least-Squares Solution to the Odometer-Camera Extrinsic Calibration Problem
相关文章:

平面运动机器人的传感器外参标定
简述 对任意两个传感器进行外参标定可以采用手眼标定算法来完成,但是,传统手眼标定算法对于运动具有一定的要求,可以证明,至少需要两个以上轴角方向不同的旋转运动才可以正确估计出外参旋转,因此,如果使用…...
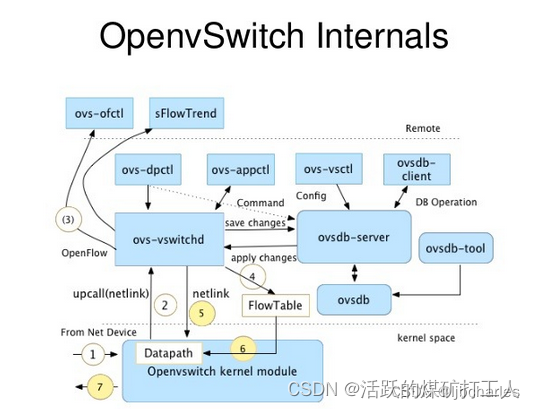
【星海随笔】SDN neutron (二) Neutron-plugin(ML2)
Neutron架构之Neutron-plugin Core-plugin(ML2)篇 Neutron-server接收两种请求: REST API请求:接收REST API请求,并将REST API分发到对应的Plugin(L3RouterPlugin)。 RPC请求:接收Plugin agent请求&#…...

野火i.MX6ULL开发板检测按键evtest(Linux应用开发)
之前一直查找不到evtest,因为没有下载成功,很可能是网络不好,下次可以软件源可以换成国内大学镜像网站。 重新断开板子电源启动,再次连接网络,下载evtest成功!!...

k8s存储
nfs 理论上nfs 其实并不是存储设备,它是一种远程共享存储服务。 k8s 存储卷 volume emptyDir:可以实现pod中的容器之间共享数据, 但是存储卷不能持久化数据,且会随着pod的生命周期一起删除。 hostpash:可以实现持久…...
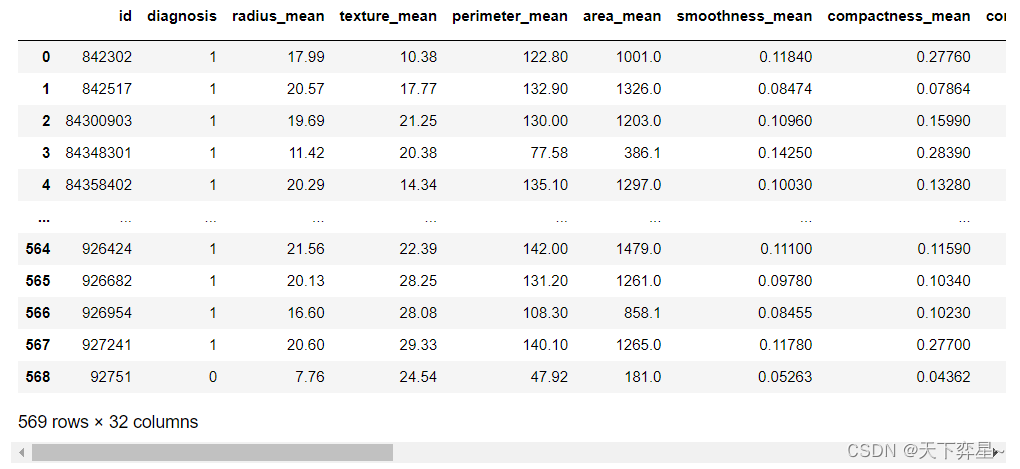
数据分析实战 | 贝叶斯分类算法——病例自动诊断分析
目录 一、数据及分析对象 二、目的及分析任务 三、方法及工具 四、数据读入 五、数据理解 六、数据准备 七、模型训练 八、模型评价 九、模型调参 十、模型预测 一、数据及分析对象 CSV文件——“bc_data.csv” 数据集链接:https://download.csdn.net/d…...
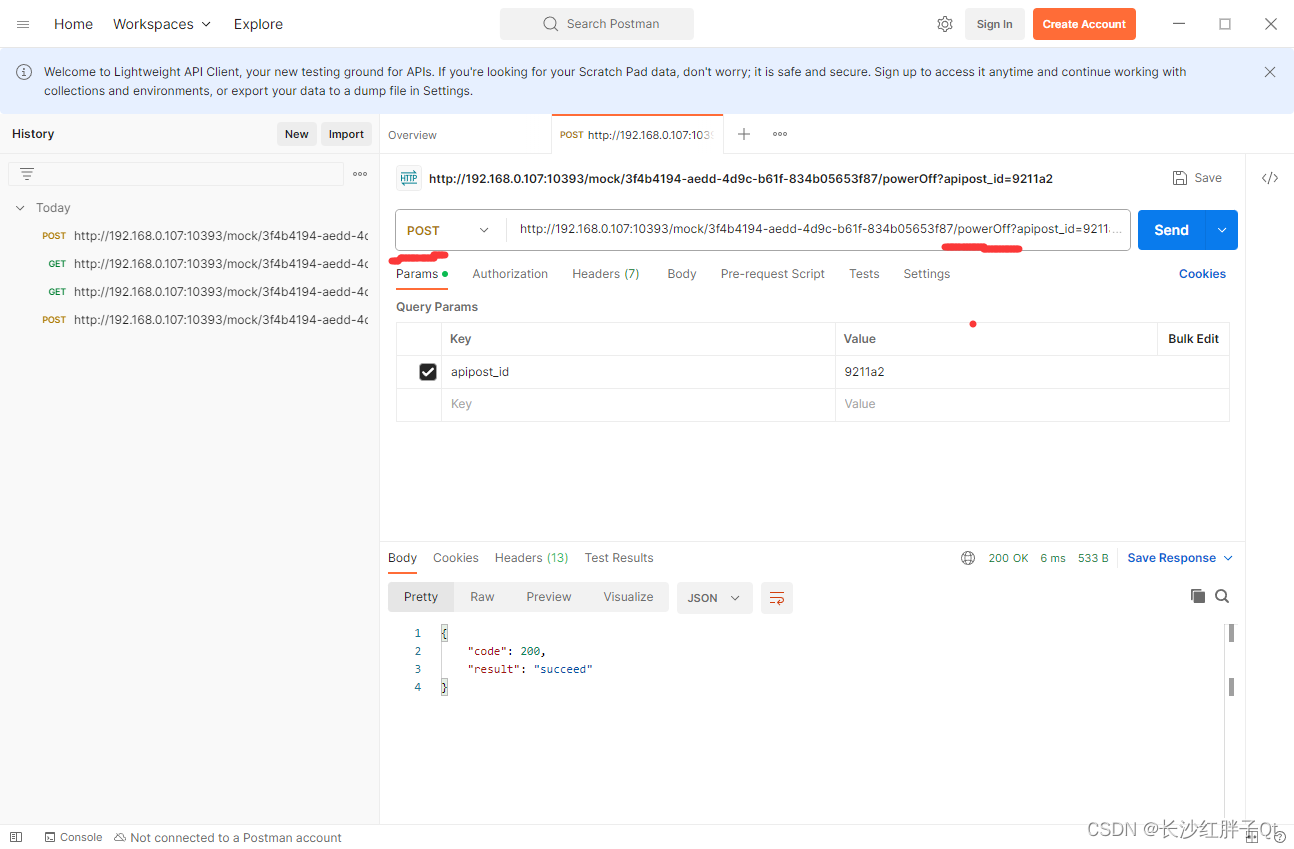
实用技巧:嵌入式人员使用http服务模拟工具模拟http服务器测试客户端get和post请求
文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/134305752 红胖子(红模仿)的博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软硬结…...

P9836 种树
容易想到分解因数。 对于一个数 p p p 的因数个数,假设它可以被分解质因数成 a 1 i 1 a 2 i 2 a 3 i 3 ⋯ a k c k a_1^{i_1} a_2^{i_2} a_3^{i_3}\cdots a_k^{c_k} a1i1a2i2a3i3⋯akck 的形式,则其因数个数为 ( i 1 1 ) ( i 2 1 )…...
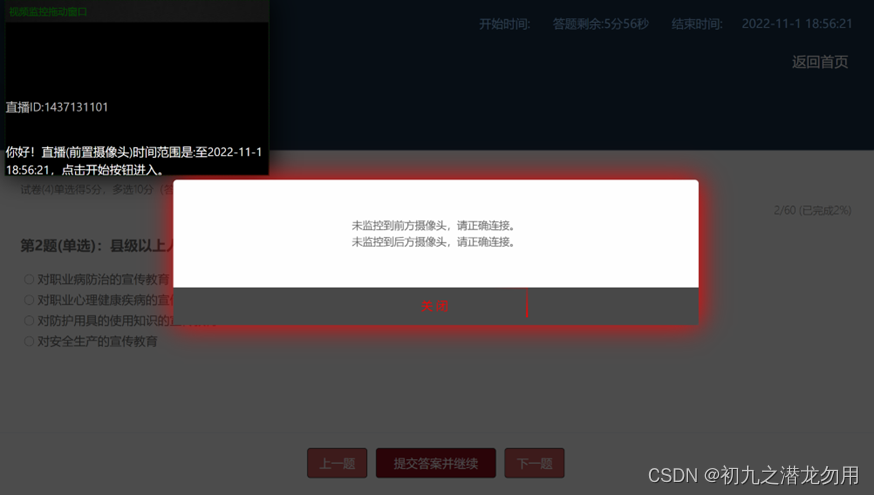
C# 查询腾讯云直播流是否存在的API实现
应用场景 在云考试中,为防止作弊行为的发生,会在考生端部署音视频监控系统,当然还有考官方监控墙系统。在实际应用中,考生一方至少包括两路直播流: (1)前置摄像头:答题的设备要求使…...
JAVA开源项目 于道前端项目 启动步骤参考
1. 安装 启动过程有9个步骤: 1.1 安装 Node JS , V18版本的 (安装步骤省略) 1.2 安装 npm install -g yarn ,node JS里边好像自带npm ,通过npm的命令安装 yarn 1.3 切换到项目中去安装,npm install &a…...
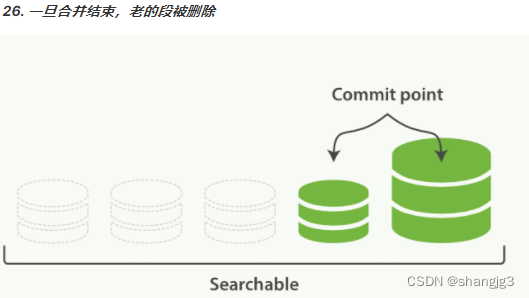
深入理解ElasticSearch分片
1. 路由计算 当索引一个文档的时候,文档会被存储到一个主分片中。 Elasticsearch 如何知道一个文档应该存放到哪个分片中呢?当我们创建文档时,它如何决定这个文档应当被存储在分片 1 还是分片 2 中呢?首先这肯定不会是随机的&…...
【Python】AppUI自动化—appium自动化元素定位、元素事件操作(17)下
文章目录 前言一.Appium 元素定位1.定位方式种类2.如何定位2.1 id定位2.2 className定位2.3 content-desc 定位2.4 Android Uiautomator定位4.1 text定位4.2 text模糊定位4.3 text正则匹配定位4.4 resourceId定位4.5 resourceId正则匹配定位4.6 className定位4.7 className正则…...

SpringBoot使用MyBatis多数据源
SpringBoot使用MyBatis多数据源 我们以 Mybatis Xml和注解两种版本为例,给大家展示如何如何配置多数据源。 1、注解方式 数据库文件: DROP TABLE IF EXISTS users; CREATE TABLE users (id bigint(20) NOT NULL AUTO_INCREMENT COMMENT 主键id,userN…...
小程序版本审核未通过,需在开发者后台「版本管理—提交审核——小程序订单中心path」设置订单中心页path,请设置后再提交代码审核
小程序版本审核未通过,需在开发者后台「版本管理—提交审核——小程序订单中心path」设置订单中心页path,请设置后再提交代码审核 因小程序尚未发布,订单中心不能正常打开查看,请先发布小程序后再提交订单中心PATH申请 初次提交…...
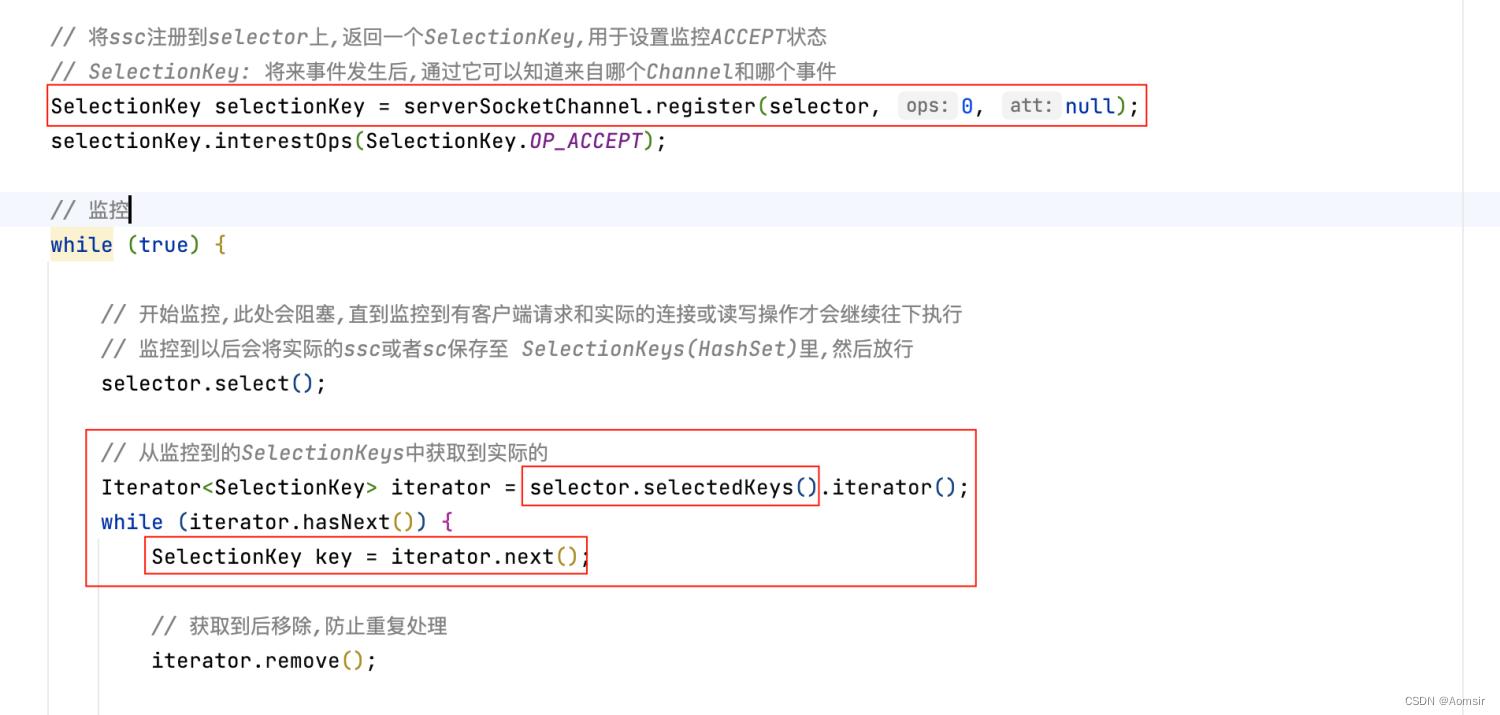
Netty入门指南之NIO Selector监管
作者简介:☕️大家好,我是Aomsir,一个爱折腾的开发者! 个人主页:Aomsir_Spring5应用专栏,Netty应用专栏,RPC应用专栏-CSDN博客 当前专栏:Netty应用专栏_Aomsir的博客-CSDN博客 文章目录 参考文献前言问题解…...

Spring Cloud学习(六)【统一网关 Gateway】
文章目录 网关的功能搭建网关服务路由断言工厂Route Predicate Factory路由过滤器 GatewayFilter过滤器执行顺序跨域问题处理 网关的功能 网关功能: 身份认证和权限校验服务路由、负载均衡请求限流 在SpringCloud中网关的实现包括两种: gatewayzuul …...

基于单片机的空调智能控制器的设计
**单片机设计介绍,基于单片机的空调智能控制器的设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机的空调智能控制器需要具备输入输出端口、定时器、计数器等模块,以便对空调进行精确控制。下…...
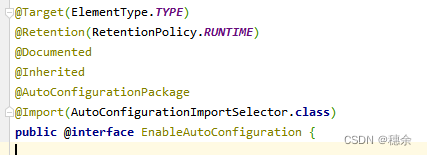
Spring Boot自动配置原理、实战、手撕自动装配源码
Spring Boot自动配置原理 相比较于传统的 Spring 应用,搭建一个 SpringBoot 应用,我们只需要引入一个注解 SpringBootApplication,就可以成功运行。 前面四个不用说,是定义一个注解所必须的,关键就在于后面三个注解&a…...

111111111111111
全局锁 就是对整个数据库进行加锁,加锁之后整个数据库就处于只读状态,后续的DML写语句,DDL语句,以及对更新事务的提交操作都会被阻塞,典型地使用场景就是做整个数据库的逻辑备份,对所有的表进行锁定&#x…...
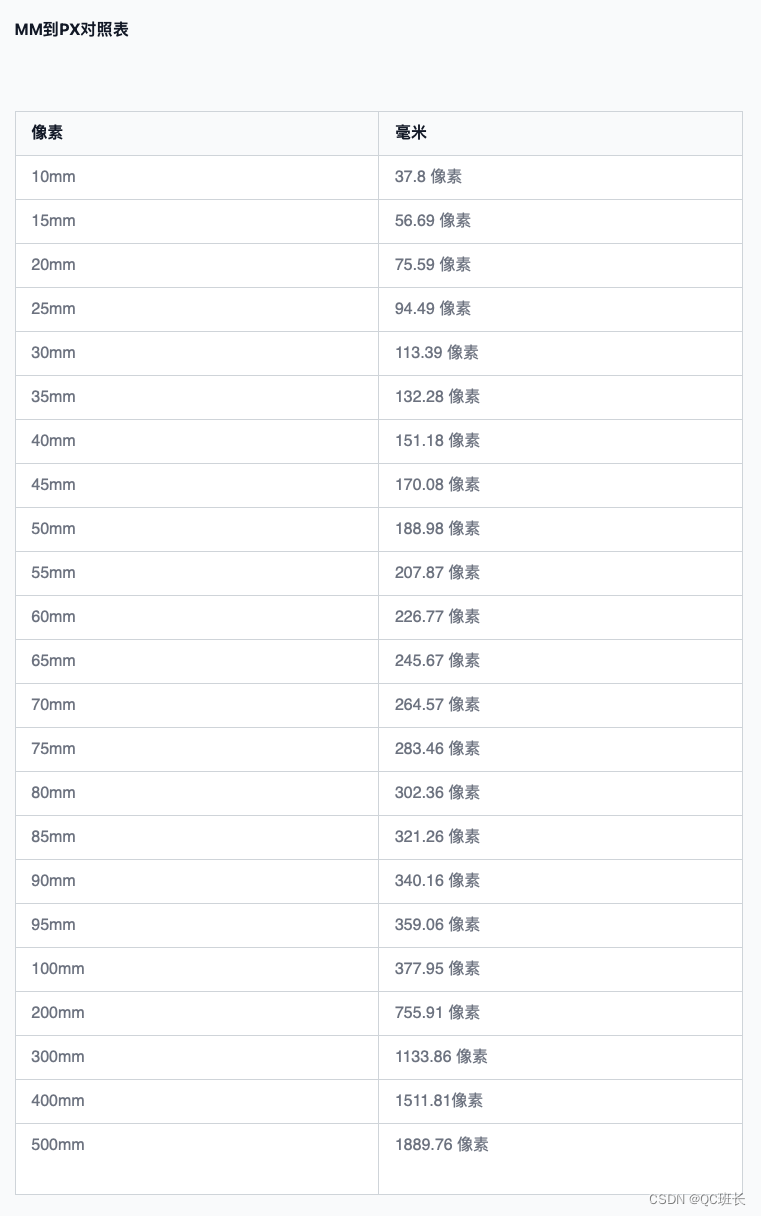
React动态生成二维码和毫米(mm)单位转像素(px)单位
一、使用qrcode.react生成二维码,qrcode.react - npm 很简单,安装依赖包,然后引用就行了 npm install qrcode.react或者 yarn add qrcode.react直接上写好的代码 import React, {useEffect, useState} from react; import QRCode from qr…...
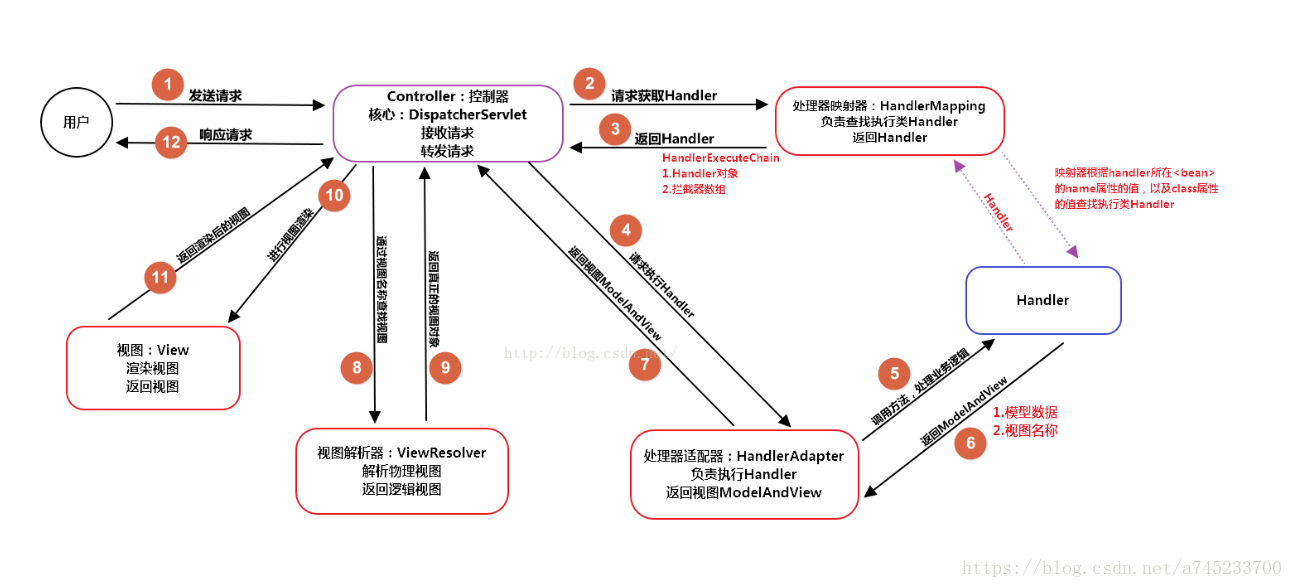
SpringMvc 常见面试题
1、SpringMvc概述 1.1、什么是Spring MVC ?简单介绍下你对springMVC的理解? Spring MVC是一个基于Java的实现了MVC设计模式的请求驱动类型的轻量级Web框架,通过把Model,View,Controller分离,将web层进行职责解耦&am…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
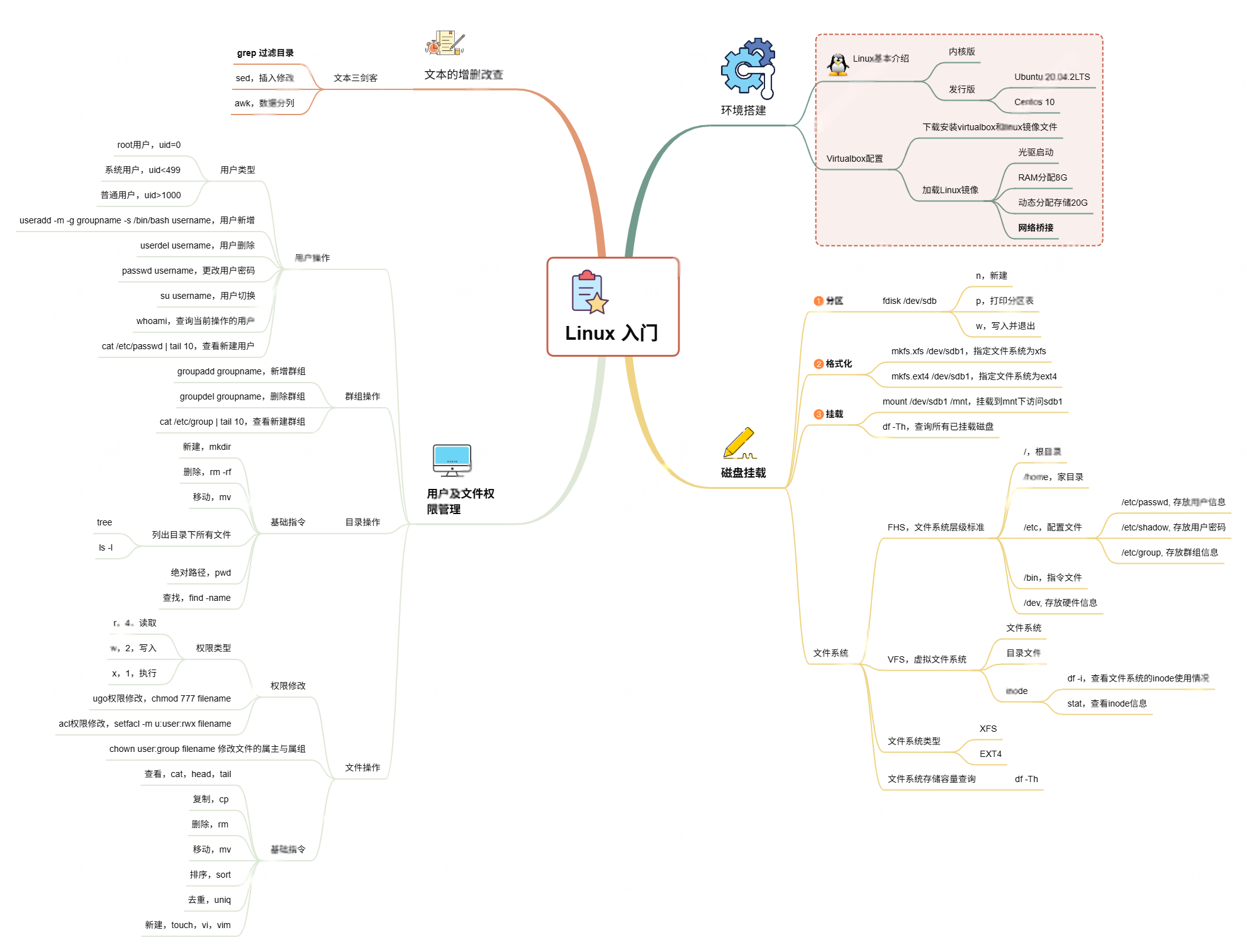
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...

Python爬虫(52)Scrapy-Redis分布式爬虫架构实战:IP代理池深度集成与跨地域数据采集
目录 一、引言:当爬虫遭遇"地域封锁"二、背景解析:分布式爬虫的两大技术挑战1. 传统Scrapy架构的局限性2. 地域限制的三种典型表现 三、架构设计:Scrapy-Redis 代理池的协同机制1. 分布式架构拓扑图2. 核心组件协同流程 四、技术实…...

【Pandas】pandas DataFrame dropna
Pandas2.2 DataFrame Missing data handling 方法描述DataFrame.fillna([value, method, axis, …])用于填充 DataFrame 中的缺失值(NaN)DataFrame.backfill(*[, axis, inplace, …])用于**使用后向填充(即“下一个有效观测值”)…...
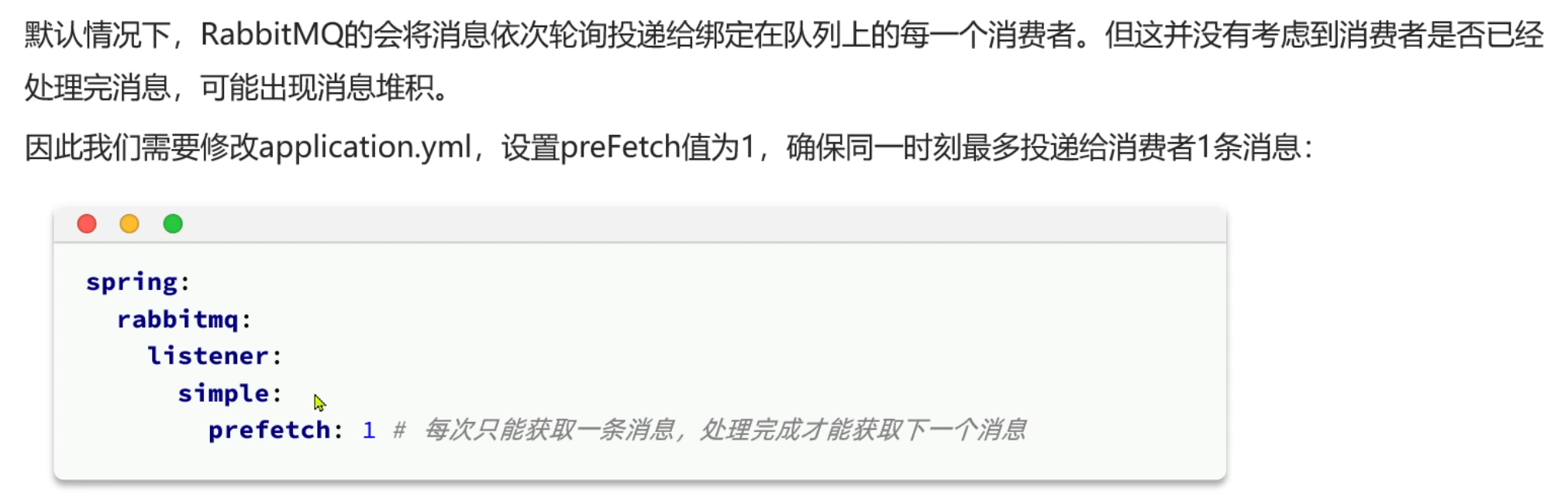
RabbitMQ work模型
Work 模型是 RabbitMQ 最基础的消息处理模式,核心思想是 多个消费者竞争消费同一个队列中的消息,适用于任务分发和负载均衡场景。同一个消息只会被一个消费者处理。 当一个消息队列绑定了多个消费者,每个消息消费的个数都是平摊的&a…...
