第 117 场 LeetCode 双周赛题解
A 给小朋友们分糖果 I
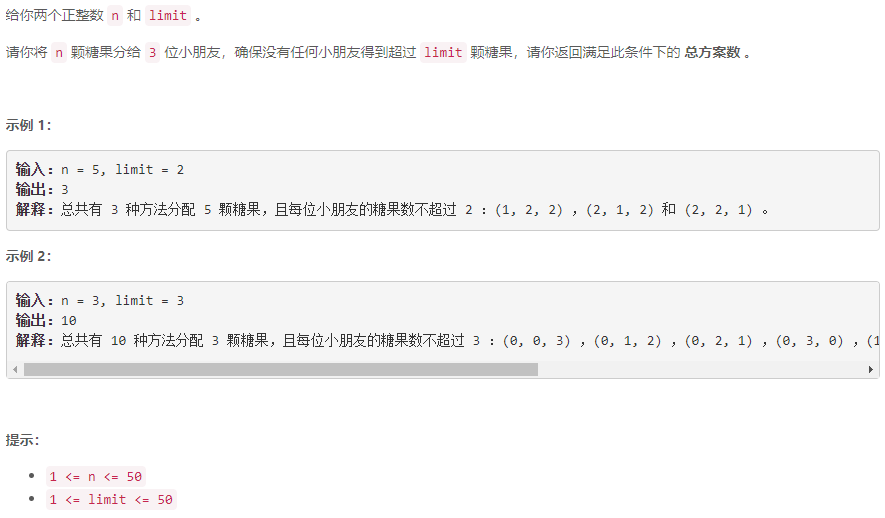
动态规划:设 p [ k ] [ i ] p[k][i] p[k][i] 为将 i i i 个糖果分给 k k k 个小朋友的方案数,先求 p [ 2 ] [ i ] p[2][i] p[2][i] ,再求 p [ 3 ] [ n ] p[3][n] p[3][n]
class Solution {
public:using ll = long long;int distributeCandies(int n, int limit) {ll p[4][n + 1];memset(p, 0, sizeof(p));for (int i = 0; i <= n; i++) {p[2][i] = min(limit, i) - max(0, i - limit) + 1;}ll res = 0;for (int i = 0; i <= limit && i <= n; i++)if (n - i <= 2 * limit)res += p[2][n - i];return res;}
};
B 给小朋友们分糖果 II

同 A A A …
class Solution {
public:using ll = long long;long long distributeCandies(int n, int limit) {ll p[4][n + 1];memset(p, 0, sizeof(p));for (int i = 0; i <= n; i++) {p[2][i] = min(limit, i) - max(0, i - limit) + 1;}ll res = 0;for (int i = 0; i <= limit && i <= n; i++)if (n - i <= 2 * limit)res += p[2][n - i];return res;}
};
C 重新排列后包含指定子字符串的字符串数目

动态规划:设 p [ i ] [ c l ] [ c t ] [ c e ] p[i][cl][ct][ce] p[i][cl][ct][ce] 为用 i i i 个字符组成的 l , t , e l,t,e l,t,e 3 3 3 种字符数分别为 c l , c t , c e cl,ct,ce cl,ct,ce 个的字符串数目, l l l 字符数 > 1 >1 >1 的字符串状态算在 c l = 1 cl=1 cl=1 的状态内,类似 t t t 字符数 > 1 >1 >1 的字符串状态算在 c t = 1 ct=1 ct=1 的状态内, e e e 字符数 > 2 >2 >2 的字符串状态算在 c e = 2 ce=2 ce=2 的状态内,答案即为 p [ n ] [ 1 ] [ 1 ] [ 2 ] p[n][1][1][2] p[n][1][1][2]
class Solution {
public:using ll = long long;ll mod = 1e9 + 7;int stringCount(int n) {ll p[n + 1][2][2][3];memset(p, 0, sizeof(p));p[0][0][0][0] = 1;//空串for (int i = 1; i <= n; i++) {for (int l = 0; l < 2; l++) {for (int t = 0; t < 2; t++) {for (int e = 0; e < 3; e++) {p[i][l][t][e] = p[i - 1][l][t][e] * 23 % mod;//第i个字符为非l,e,t的字符if (l) {//第i个字符为lp[i][l][t][e] += (p[i - 1][l - 1][t][e] + p[i - 1][l][t][e]) % mod;p[i][l][t][e] %= mod;}if (t) {//第i个字符为tp[i][l][t][e] += (p[i - 1][l][t - 1][e] + p[i - 1][l][t][e]) % mod;p[i][l][t][e] %= mod;}if (e) {//第i个字符为ep[i][l][t][e] += p[i - 1][l][t][e - 1];p[i][l][t][e] %= mod;if (e == 2) {p[i][l][t][e] += p[i - 1][l][t][e];p[i][l][t][e] %= mod;}}}}}}return (p[n][1][1][2] + mod) % mod;}
};
D 购买物品的最大开销


贪心 + 优先级队列:每次购买当前各商店最右商品价格最小的最右商品即可获得最大总开销,用优先级队列维护各商店最右商品价格最小值
class Solution {
public:using ll = long long;long long maxSpending(vector<vector<int>> &values) {int m = values.size(), n = values[0].size();priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<>> heap;//最小堆for (int i = 0; i < m; i++)heap.emplace(values[i][n - 1], i, n - 1);ll res = 0;for (int i = 1; i <= m * n; i++) {auto [v, r, c] = heap.top();heap.pop();res += 1LL * i * v;if (c)//该商店还有剩余商品heap.emplace(values[r][c - 1], r, c - 1);}return res;}
};
相关文章:

第 117 场 LeetCode 双周赛题解
A 给小朋友们分糖果 I 动态规划:设 p [ k ] [ i ] p[k][i] p[k][i] 为将 i i i 个糖果分给 k k k 个小朋友的方案数,先求 p [ 2 ] [ i ] p[2][i] p[2][i] ,再求 p [ 3 ] [ n ] p[3][n] p[3][n] class Solution { public:using ll long …...

OpenCV C++ 图像处理实战 ——《多二维码识别》
OpenCV C++ 图像处理实战 ——《多二维码识别》 一、结果演示二、zxing库配置2.1下载编译三、多二维码识别3.1 Method one3.1.1 源码3.2 Method two3.2.1 源码四、源码测试图像下载总结一、结果演示 </...
)
经典算法(查找与排序)
查找 顺序查找 顺序查找(Linear Search)是一种在有序数组中查找目标元素的基本算法。它的时间复杂度为 O(n),适用于查找少量数据。顺序查找的基本思想是从数组的第一个元素开始,逐个与待查找的元素进行比较,直到找到…...

微软和Red Hat合体:帮助企业更方便部署容器
早在2015年,微软就已经和Red Hat达成合作共同为企业市场开发基于云端的解决方案。时隔两年双方在企业市场的多个方面开展更紧密的合作,今天两家公司再次宣布帮助企业更方便地部署容器。 双方所开展的合作包括在微软Azure上部署Red Hat OpenShift…...
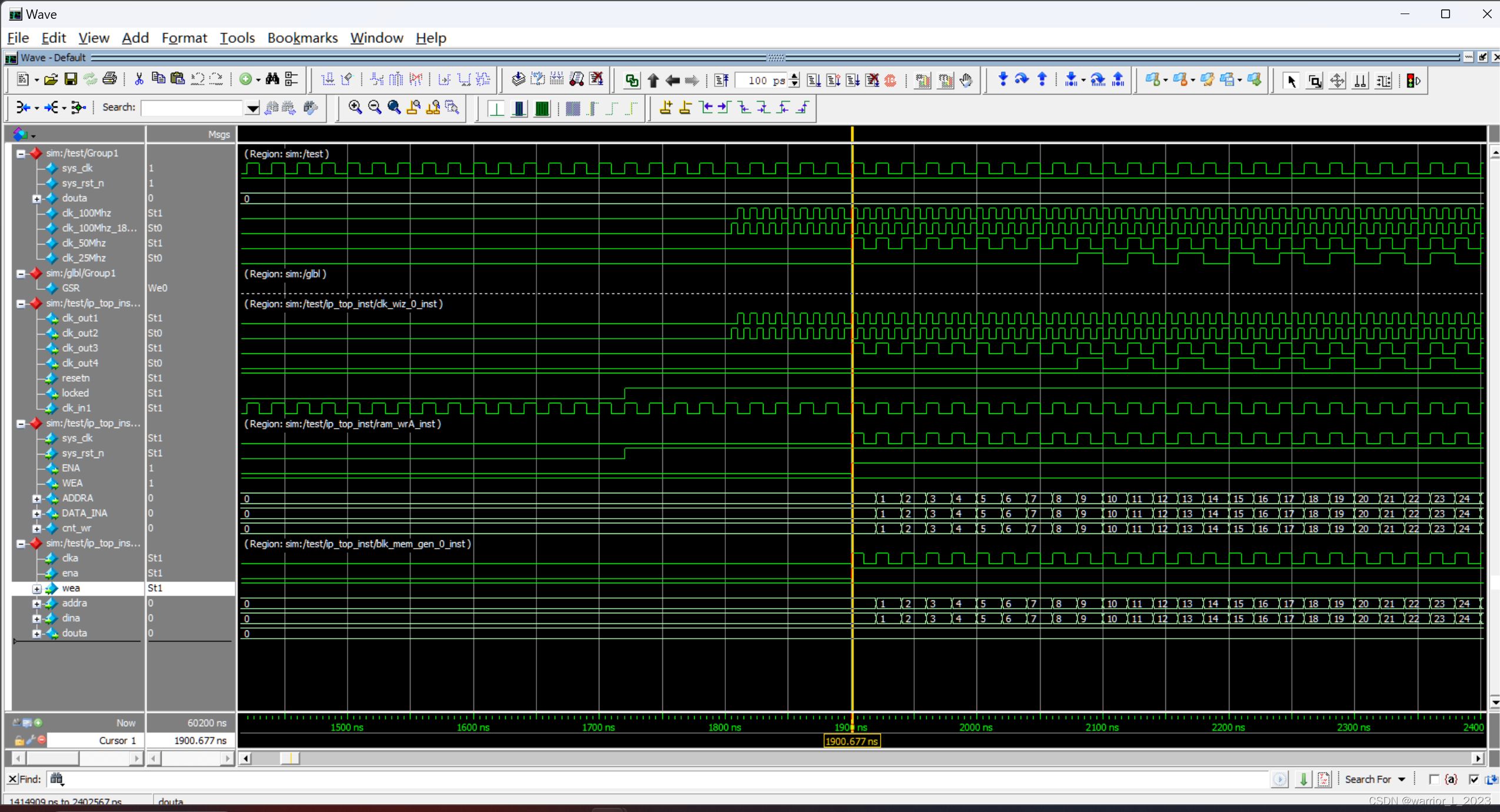
ZYNQ_project:IP_ram_pll_test
例化MMCM ip核,产生100Mhz,100Mhz并相位偏移180,50Mhz,25Mhz的时钟信号。 例化单口ram,并编写读写控制器,实现32个数据的写入与读出。 模块框图: 代码: module ip_top(input …...
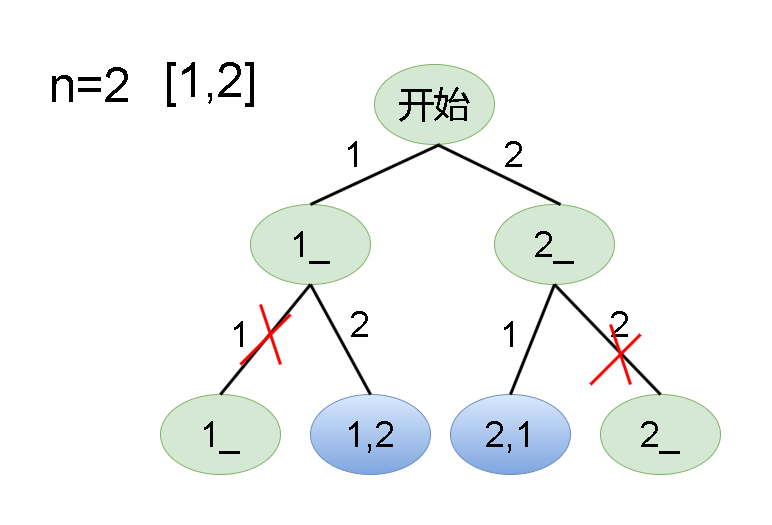
Leetcode刷题详解——优美的排列
1. 题目链接:526. 优美的排列 2. 题目描述: 假设有从 1 到 n 的 n 个整数。用这些整数构造一个数组 perm(下标从 1 开始),只要满足下述条件 之一 ,该数组就是一个 优美的排列 : perm[i] 能够被…...
[PHP]Kodexplorer可道云 v4.47
KodExplorer可道云,原名芒果云,是基于Web技术的私有云和在线文件管理系统,由上海岱牧网络有限公司开发,发布于2012年6月。致力于为用户提供安全可控、可靠易用、高扩展性的私有云解决方案。 用户只需通过简单环境搭建,…...

C/C++数字判断 2021年9月电子学会青少年软件编程(C/C++)等级考试一级真题答案解析
目录 C/C数字判断 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 四、程序说明 五、运行结果 六、考点分析 C/C数字判断 2021年9月 C/C编程等级考试一级编程题 一、题目要求 1、编程实现 输入一个字符,如何输入的字符是数字&#x…...

云栖大会丨桑文锋:打造云原生数字化客户经营引擎
近日,2023 云栖大会在杭州举办。今年云栖大会回归了 2015 的主题:「计算,为了无法计算的价值」。神策数据创始人 & CEO 桑文锋受邀出席「生态产品与伙伴赋能」技术主题,并以「打造云原生数字化客户经营引擎」为主题进行演讲。…...

如何用java写一个网站:从零搭建个性化网站
随着互联网的迅猛发展,Java作为一种强大而灵活的编程语言,为构建各类网站提供了丰富的解决方案。本文将探讨如何使用Java编写一个个性化网站,并通过具体实例进行深入分析。 第一步:选择适当的技术栈 在着手构建网站之前࿰…...
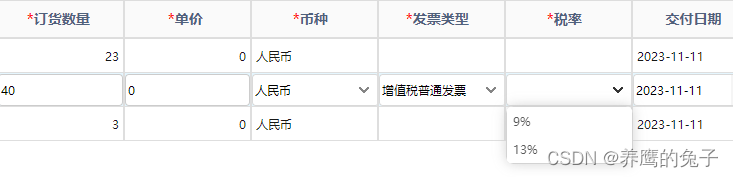
Easyui DataGrid combobox联动下拉框内容
发票信息下拉框联动,更具不同的发票类型,显示不同的税率 专票 普票 下拉框选择事件 function onSelectType(rec){//选中值if (rec2){//普通发票对应税率pmsPlanList.pmsInvoiceTaxRatepmsPlanList.pmsInvoiceTaxRateT}else {//专用发票对应税率pmsPlan…...

力扣学习笔记——11. 盛最多水的容器
链接:https://leetcode.cn/problems/container-with-most-water/ 11. 盛最多水的容器 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的…...

Spring Boot: 约定优于配置的软件设计思想
文章目录 传统Spring框架的繁琐配置1. **管理jar包依赖**2. **维护web.xml**3. **维护Dispatch-Servlet.xml配置项**4. **应用部署到Web容器**5. **第三方组件集成到Spring IOC容器中的配置项维护** Spring Boot的简化与自动化1. Spring Boot Starter启动依赖2. 自动装配机制3.…...
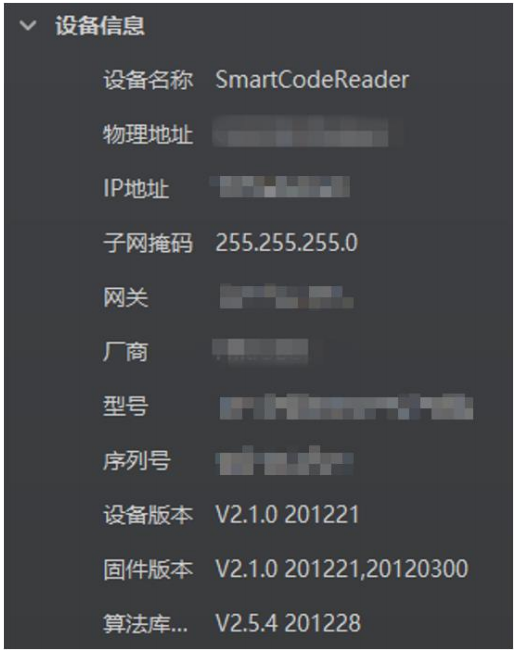
TCP触发海康扫码相机S52CN-IC-JQR-NNN25
PC环境设置 为保证客户端正常运行以及数据传输的稳定性,在使用客户端软件前,需要对 PC 环境 进行设置 关闭防火墙 操作步骤如下: 1. 打开系统防火墙。 2. 在自定义设置界面中,选择关闭防火墙的对应选项,并单击…...
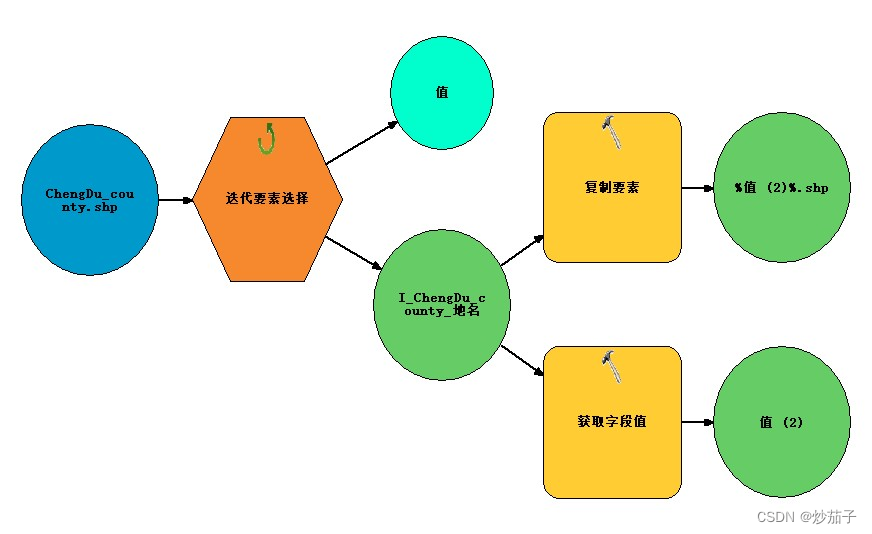
ArcGIS:如何迭代Shp文件所有要素并分别导出为Shp文件?
01 前言 尝试用IDL实现,奈何又涉及新的类IDLffShape,觉得实在没有必要学习的必要,毕竟不是搞开发,只是做做数据处理,没必要拿IDL不擅长的且底层的东西自己造轮子。 这里想到使用Python去解决,gdal太久没用…...

[工业自动化-11]:西门子S7-15xxx编程 - PLC从站 - 分布式IO从站/从机
目录 一、什么是以分布式IO从站/从机 二、分布式IO从站的意义 三、ET200分布式从站系列 一、什么是以分布式IO从站/从机 在工业自动化领域中,分布式 IO 系统是目前应用最为广泛的一种 I/O 系统,其中分布式 IO 从站是一个重要的组成部分。 分布式 IO …...
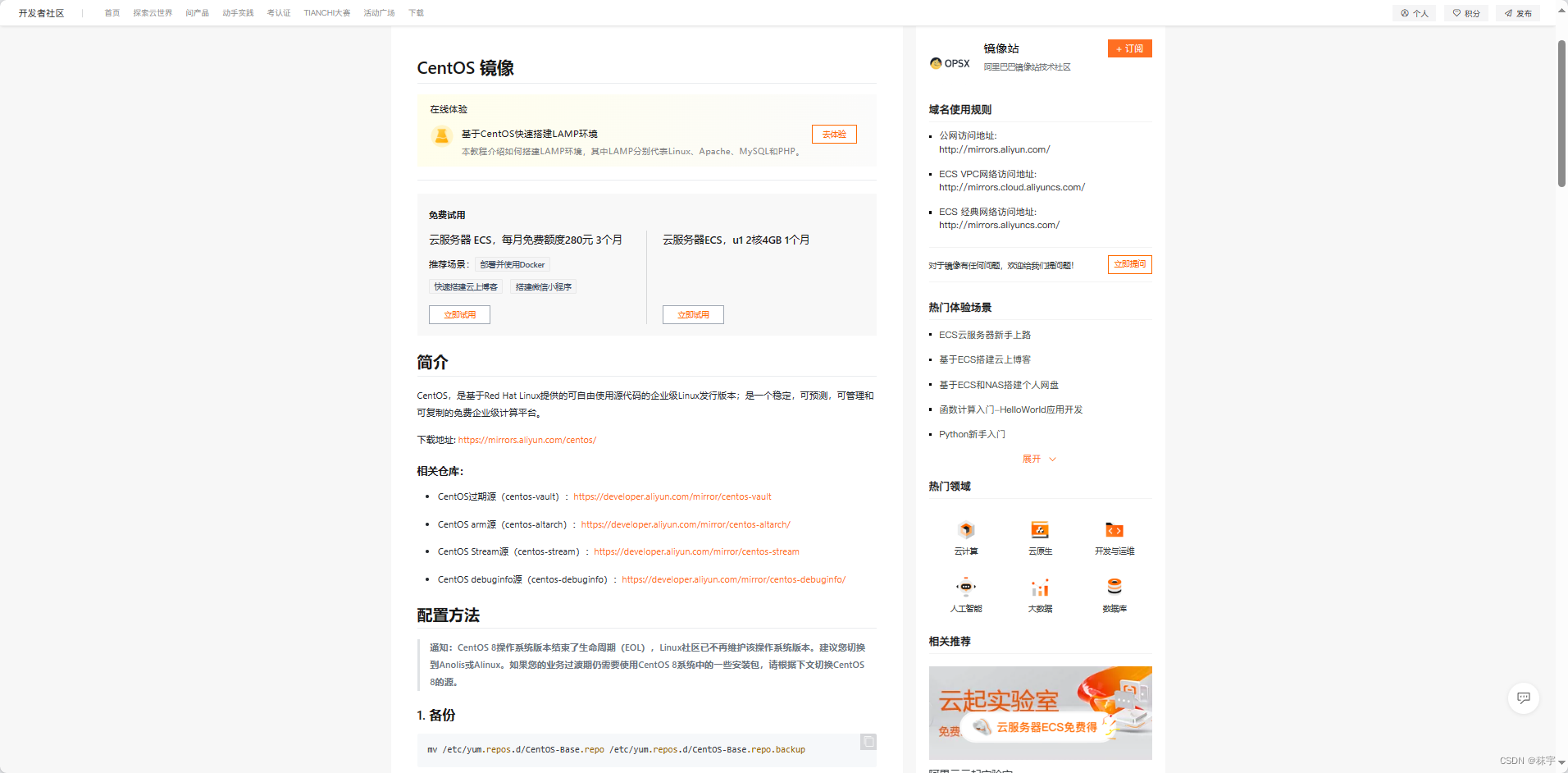
Linux技能篇-yum源搭建(本地源和公网源)
文章目录 前言一、yum源是什么?二、使用镜像搭建本地yum源1.搭建临时仓库第一步:挂载系统ios镜像到虚拟机第二步:在操作系统中挂载镜像第三步:修改yum源配置文件 2.搭建本地仓库第一步:搭建临时yum源来安装httpd并做文…...
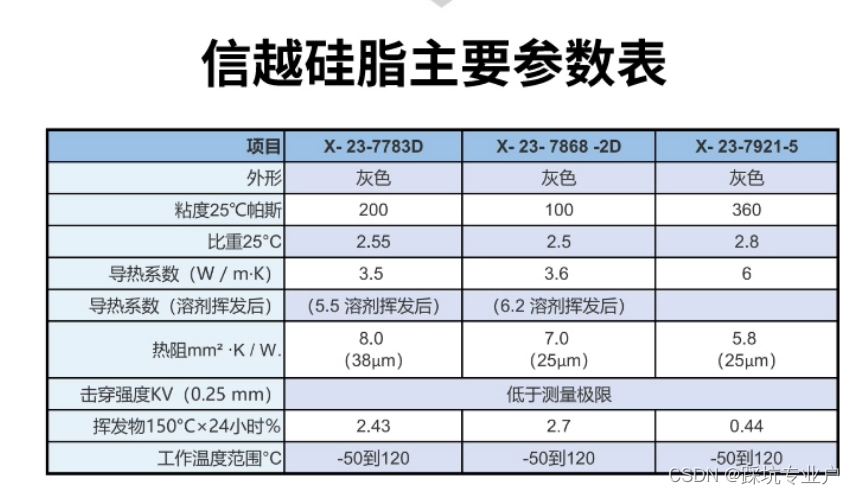
电脑清灰涂硅脂后电脑CPU温度不降反升
目录 一.问题描述二.问题解决三.拆机注意事项四.影响散热的主要因素说明1.通风差2.硅脂材料差3.硅脂涂抹方式错误 一.问题描述 电脑型号:暗影精灵5 测温工具:硬件狗狗(只要是测温软件都可以,比如omen hub和Core Temp…࿰…...
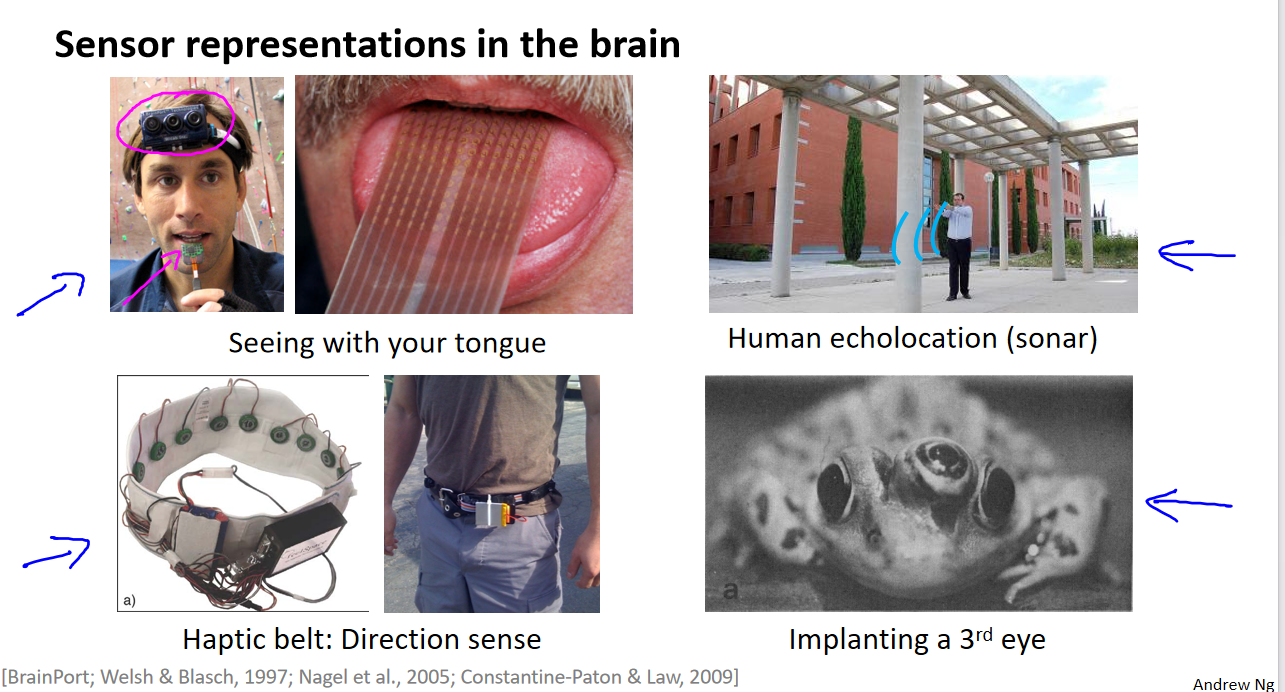
吴恩达《机器学习》8-1->8-2:非线性假设、神经元和大脑
一、非线性假设 在之前学到的线性回归和逻辑回归中,存在一个缺点,即当特征数量很多时,计算的负荷会变得非常大。考虑一个例子,假设我们使用 𝑥₁, 𝑥₂ 的多项式进行预测,这时我们可以很好地应…...

services.Jenkins Additional property tags is not allowed
今天需要给Jenkins server添加几个tag,于是就在docker的compose文件中添加了如下的tags, version: "3.9" services:jenkins:image: testbuild: context: services/jenkinsargs:- jenkins_version2.346.2- plugin_cli_version2.9.3volumes:- j…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
