力扣第72题 编辑距离 (增 删 改) C++ 动态规划 附Java代码
题目
72. 编辑距离
中等
相关标签
字符串 动态规划
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros" 输出:3 解释: horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution" 输出:5 解释: intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u')
提示:
0 <= word1.length, word2.length <= 500word1和word2由小写英文字母组成
思路和解题方法
具体来说,对于给定的两个字符串
word1和word2,首先创建一个二维数组dp来保存它们之间的编辑距离。然后,分别初始化数组的第一行和第一列,使得dp[i][0] = i和dp[0][j] = j,其中i和j分别表示字符串word1和word2的长度。这样初始化是为了表示将word1和空串(或者将word2和空串)进行匹配时的编辑距离。接下来,从第二行和第二列开始,对于每个位置
(i,j),先判断word1和word2在当前位置上的字符是否相同。如果相同,则说明不需要进行任何编辑操作,因此dp[i][j]可以直接继承上一个位置的编辑距离,即dp[i-1][j-1]。否则,需要在上一个位置的编辑距离的基础上增加一些编辑操作,例如插入、删除或替换字符等。这时,可以考虑三种情况,并选择其中编辑距离最小的一种:
在
word1的第i个位置插入一个字符,使得word1和word2的前j个字符相同,此时编辑距离为dp[i][j-1] + 1。在
word1的第i个位置删除一个字符,使得word1的前i-1个字符和word2的前j个字符相同,此时编辑距离为dp[i-1][j] + 1。在
word1的第i个位置替换一个字符,使得word1和word2的前i个字符和j个字符分别相同,此时编辑距离为dp[i-1][j-1] + 1。因此,对于每个位置
(i,j),可以使用如下递推公式来计算最小的编辑距离:if (word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1]; else dp[i][j] = min({dp[i-1][j-1], dp[i-1][j], dp[i][j-1]}) + 1;其中,
min({dp[i-1][j-1], dp[i-1][j], dp[i][j-1]})表示选取上述三种编辑操作中编辑距离最小的一种,加上一次操作所需的编辑距离1,即可得到当前位置(i,j)的最小编辑距离。最后,返回
dp[w1][w2],即两个字符串的完全匹配所需的最小编辑距离。
复杂度
时间复杂度:
O(n*n)
时间复杂度为 O(n*n),其中 n 为两个字符串的长度之和。这是因为算法使用了一个二维数组存储子问题的解,需要计算该数组中所有 n*n 个位置的值。
空间复杂度
O(n*n)
空间复杂度也为 O(n*n),因为需要使用一个二维数组来存储所有子问题的解。
如果想要将空间复杂度优化到 O(n) 级别,则可以使用滚动数组的技巧,只保留当前行和上一行的值即可,但会使得代码实现稍微有些复杂。
c++ 代码
class Solution {
public:int minDistance(string word1, string word2) {int w1 = word1.size(), w2 = word2.size();// 定义一个二维动态数组 dp,其中 dp[i][j] 表示将 word1 的前 i 个字符转换为 word2 的前 j 个字符所需要的最少操作次数。vector<vector<int>> dp(w1+1, vector<int>(w2+1, 0));// 初始化第一行和第一列,即将一个空字符串转换成另一个字符串所需的最少操作次数。for(int i = 0; i <= w1; i++) dp[i][0] = i;for(int j = 0; j <= w2; j++) dp[0][j] = j;// 从第二行和第二列开始,按照状态转移方程进行计算。for(int i = 1; i <= w1; i++) {for(int j = 1; j <= w2; j++) {// 如果 word1 的第 i 个字符与 word2 的第 j 个字符相等,则不需要进行任何操作。if(word1[i-1] == word2[j-1])dp[i][j] = dp[i-1][j-1];// 如果 word1 的第 i 个字符与 word2 的第 j 个字符不相等,则需要进行以下三种操作中的一种来进行转换操作:// 1. 在 word1 中插入一个字符;// 2. 在 word2 中插入一个字符;// 3. 替换 word1 中的第 i 个字符或者 word2 中的第 j 个字符。elsedp[i][j] = min({dp[i-1][j-1], dp[i-1][j], dp[i][j-1]}) + 1;}}// 返回将 word1 转换成 word2 的最少操作次数。return dp[w1][w2];}
};
Java代码
- 首先获取两个字符串的长度,即
word1.length()和word2.length(),分别赋值给变量m和n。- 接下来,创建一个二维数组
dp,大小为(m + 1) × (n + 1),用于保存计算过程中的编辑距离。这里多加了一行和一列是为了存储空串与word1或word2的匹配情况。- 然后,通过两个嵌套的循环遍历数组
dp中的每个位置(i, j),其中i表示word1的前i个字符,j表示word2的前j个字符。- 对于每个位置
(i, j),首先判断word1和word2在当前位置上的字符是否相同,即word1.charAt(i - 1) == word2.charAt(j - 1)。如果相同,则说明不需要进行任何编辑操作,所以将dp[i][j]的值设置为dp[i - 1][j - 1],即继承上一个位置的编辑距离。- 如果不相同,则需要考虑插入、删除和替换字符三种编辑操作中的最小编辑距离。这里使用
Math.min方法来取得三者中的最小值,并加上一次操作所需的编辑距离1,即Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1,然后将结果赋值给dp[i][j]。- 最后,返回
dp[m][n],即两个字符串的完全匹配所需的最小编辑距离。
class Solution {public int minDistance(String word1, String word2) {// 获取两个字符串的长度int m = word1.length();int n = word2.length();// 创建一个二维数组来保存编辑距离int[][] dp = new int[m + 1][n + 1];// 初始化dp数组的第一行和第一列for (int i = 1; i <= m; i++) {dp[i][0] = i;}for (int j = 1; j <= n; j++) {dp[0][j] = j;}// 逐行逐列计算编辑距离for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {// 判断当前字符是否相同if (word1.charAt(i - 1) == word2.charAt(j - 1)) {// 如果相同,则不需要进行任何编辑操作dp[i][j] = dp[i - 1][j - 1];} else {// 如果不同,则需要进行插入、删除或替换等操作,选取其中编辑距离最小的一种dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;}}}// 返回编辑距离数组的最后一个元素,即两个字符串的完全匹配所需的最小编辑距离return dp[m][n];}
}
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:
 C++ 动态规划 附Java代码)
力扣第72题 编辑距离 (增 删 改) C++ 动态规划 附Java代码
题目 72. 编辑距离 中等 相关标签 字符串 动态规划 给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。 你可以对一个单词进行如下三种操作: 插入一个字符删除一个字符替换一个字符 示例 1: 输入&a…...
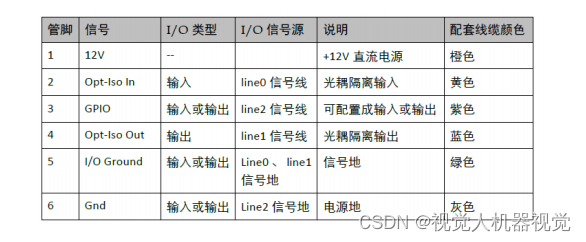
工业相机基本知识理解:工业相机IO接口,功耗和供电方式
I-input 相机接收外部信号,可用于触发相机(硬触发),也可用于定制不同的 功能,例如使用不同信号宽度来改变相机的曝光时间。主要用于现场设 备控制相机使用,常常配合各种传感器使用 O-output 相机输出信号&a…...

数据库设计
数据库设计特点 数据库建设的基本规律:三分技术,七分管理,十二分基础数据结构(数据)设计和行为(处理)设计相结合:数据库设计应该和应用系统设计相结合 数据库设计方法 新奥尔良方…...

【react.js + hooks】使用 useLoading 控制加载
在页面上 loading(加载)的效果十分常见,在某些场景下,一个页面上甚至可能有特别多的 loading 存在,此时为每一个 loading 专门创建一个 state 显然太过繁琐,不如试试写一个 useLoading 来集中管理ÿ…...
Cordova系列之化繁为简:打造全场景适用的Cordova组件
前言 在我之前的文章 Cordova初探 的开篇中说到了Cordova在Android应用开发中的一个显著的局限性就是我们的Activity必须继承其提供的CordovaActivity。这种设计对于那些追求个性化UI设计的项目而言,显得尤为受限。 其实也可以理解,Cordova主要旨在为前…...

Flink之Catalog
Catalog Catalog概述Catalog分类 GenericInMemoryCatalogJdbcCatalog下载JAR包及使用重启操作创建Catalog查看与使用Catalog自动初始化catalog HiveCatalog下载JAR包及使用重启操作hive metastore服务创建Catalog查看与使用CatalogFlink与Hive中操作自动初始化catalog 用户自定…...

计算机网络——物理层-传输方式(串行传输、并行传输,同步传输、异步传输,单工、半双工和全双工通信)
目录 串行传输和并行传输 同步传输和异步传输 单工、半双工和全双工通信 串行传输和并行传输 串行传输是指数据是一个比特一个比特依次发送的。因此在发送端和接收端之间,只需要一条数据传输线路即可。 并行传输是指一次发送n个比特,而不是一个比特&…...
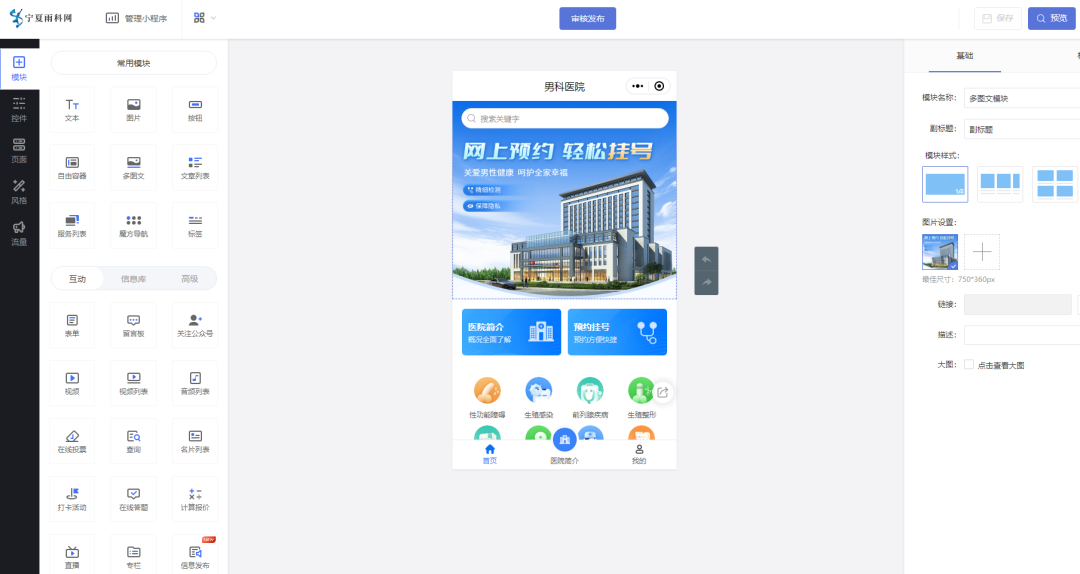
男科医院服务预约小程序的作用是什么
医院的需求度从来都很高,随着技术发展,不少科目随之衍生出新的医院的,比如男科医院、妇科医院等,这使得目标群体更加精准,同时也赋能用户可以快速享受到服务。 当然相应的男科医院在实际经营中也面临痛点:…...
有没有实时检测微信聊天图片的软件,只要微信收到了有二维码的图片就把它提取出来?
10-2 如果你有需要自动并且快速地把微信收到的二维码图片保存到指定文件夹的需求,那本文章非常适合你,本文章教你如何实现自动保存微信收到的二维码图片到你指定的文件夹中,助你快速扫码,比别人领先一步。 首先需要准备好的材料…...

core-site.xml,yarn-site.xml,hdfs-site.xml,mapred-site.xml配置
core-site.xml <?xml version"1.0" encoding"UTF-8"?> <?xml-stylesheet type"text/xsl" href"configuration.xsl"?> <!--Licensed under the Apache License, Version 2.0 (the "License");you may no…...
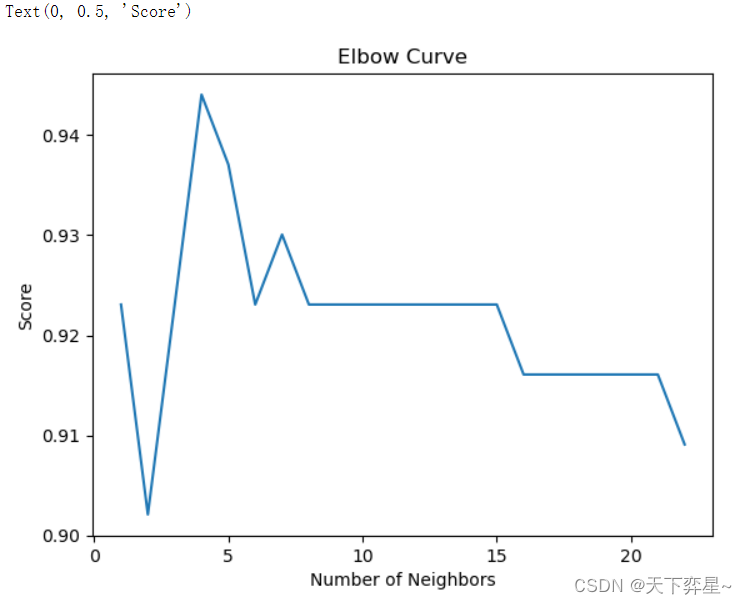
数据分析实战 | KNN算法——病例自动诊断分析
目录 一、数据及分析对象 二、目的及分析任务 三、方法及工具 四、数据读入 五、数据理解 六、数据准备 七、模型训练 八、模型评价 九、模型调参 十、模型改进 十一、模型预测 一、数据及分析对象 CSV文件——“bc_data.csv” 数据集链接:https://dow…...
JS实现数据结构与算法
队列 1、普通队列 利用数组push和shif 就可以简单实现 2、利用链表的方式实现队列 class MyQueue {constructor(){this.head nullthis.tail nullthis.length 0}add(value){let node {value}if(this.length 0){this.head nodethis.tail node}else{this.tail.next no…...

计算机毕业设计 基于SpringBoot的驾校管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...
S7-1200PLC和SMART PLC开放式以太网通信(UDP双向通信)
S7-1200PLC的以太网通信UDP通信相关介绍还可以参考下面文章链接: 博途PLC开放式以太网通信TRCV_C指令应用编程(运动传感器UDP通信)-CSDN博客文章浏览阅读2.8k次。博途PLC开放式以太网通信TSENG_C指令应用,请参看下面的文章链接:博途PLC 1200/1500PLC开放式以太网通信TSEND_…...

作用域插槽slot-scope
一般用于组件封装,将使用props传入组件的数据再次调出来或者单纯调用组件中的数据。也可用于为组件某个部分自定义样式以及为某次使用组件自定义样式。 直接拿elementui的el-table举例: <template><el-table v-loading"loading&q…...

Redis学习笔记13:基于spring data redis及lua脚本list列表实现环形结构案例
工作过程中需要用到环形结构,确保环上的各个节点数据唯一,如果有新的不同数据到来,则将最早入环的数据移除,每次访问环形结构都自动刷新有效期;可以基于lua 的列表list结构来实现这一功能,lua脚本可以节省网…...

c# 将excel导入 sqlite
nuget 须要加载 EPPlus.Core ExcelDataReader ExcelDataReader.DataSet //需要引用的扩展 using ExcelDataReader; using ExcelPackage OfficeOpenXml.ExcelPackage; public static void CreateZhouPianChaTable(){string tbname "zhou_pian_cha1";//判断表是否存…...

KafkaConsumer 消费逻辑
版本:kafka-clients-2.0.1.jar 之前想写个插件修改 kafkaConsumer 消费者的逻辑,根据 header 过滤一些消息。于是需要了解一下 kafkaConsumer 具体是如何拉取消费消息的,确认在消费之前过滤掉消息是否会有影响。 下面是相关的源码࿰…...
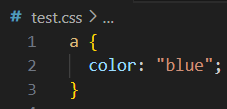
scss 实用教程
变量 $ 定义变量 $link-color: blue;变量名可以与css中的属性名和选择器名称相同 使用变量 a {color: $link_color; }$highlight-border: 1px solid $link_color;中划线和下划线相互兼容,即中划线声明的变量可以使用下划线的方式引用,反之亦然。 $li…...
NO.304 二维区域和检索 - 矩阵不可变
题目 给定一个二维矩阵 matrix,以下类型的多个请求: 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, col1) ,右下角 为 (row2, col2) 。 实现 NumMatrix 类: NumMatrix(int[][] matrix) 给定整数矩阵 …...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
