强化学习中蒙特卡罗方法
一、蒙特卡洛方法
这里将介绍一个学习方法和发现最优策略的方法,用于估计价值函数。与前文不同,这里我们不假设完全了解环境。蒙特卡罗方法只需要经验——来自实际或模拟与环境的交互的样本序列的状态、动作和奖励。从实际经验中学习是引人注目的,因为它不需要任何关于环境动态的先验知识,但仍然可以实现最优行为。从模拟经验中学习也很强大。尽管需要一个模型,但该模型只需要生成样本转换,而不是动态规划所需的完整概率分布的所有可能转换。令人惊讶的是,在很多情况下,根据所需概率分布生成经验样本很容易,但获得分布的显式形式是不可行的。
蒙特卡罗方法是解决强化学习问题的方法,它基于平均样本回报。为了确保可定义回报可用,在这里我们将蒙特卡罗方法仅定义为针对离散任务的方法。即我们假设经验分为回合,并且所有回合最终都会终止,无论选择什么动作。只有在完成回合后才会更改价值估计和策略。因此,蒙特卡罗方法可以是逐回合的增量,但不能是逐步(在线)的增量。术语“蒙特卡罗”通常更广泛地用于任何涉及大量随机组件的估计方法。在这里,我们将其专门用于基于平均完整回报(而不是从部分回报中学习的方法)的方法。
蒙特卡罗方法对每个状态-动作对进行采样和平均回报,就像我们在前文对每个动作进行采样和平均奖励一样。主要的区别在于,现在有多个状态,每个状态都像不同的问题(如联想搜索或上下文)一样,而且这些不同的问题是相互关联的。也就是说,在一个状态下采取一个行动后的回报取决于在同一回合中后来采取的行动。因为所有的行动选择都在进行学习,所以从更早的状态来看,这个问题就变成了非平稳的。
为了处理非平稳性,我们采用了通用策略迭代(GPI)的想法。在那里,我们从MDP的知识中计算值函数,在这里,我们从样本回报中学习值函数与相应的策略仍然以相同的方式相互作用以获得最优性(GPI)。与DP一样,我们首先考虑预测问题(计算固定任意策略π的vπ和qπ),然后进行政策改进,最后是控制问题以及通过GPI解决。这些来自DP的想法都被扩展到了只有样本经验可用的蒙特卡罗情况下。
二、蒙特卡洛预测
我们首先考虑使用蒙特卡罗方法学习给定策略的状态值函数。注意,一个状态的值是期望的回报,也就是从该状态开始的期望累积未来折扣奖励。那么,从经验中估计它的一个明显方法就是简单地将该状态后观察到的回报进行平均。随着更多的回报被观察到,平均值应该收敛到期望值。这个想法是所有蒙特卡罗方法的基础。
特别是,假设我们希望估计π策略下状态s的值vπ(s),给定一组遵循π并通过s获得的状态转移序列。在每个回合中,状态s的每次出现称为对s的一次。当然,在同一个回合中,s可能被多次;让我们称在回合中对s的第一次为s的第一次。第一次蒙特卡罗方法估计vπ(s)为在第一次s后的回报的平均值,而每次蒙特卡罗方法则将所有s后的回报进行平均。这两种蒙特卡罗方法非常相似,但具有稍微不同的理论性质。蒙特卡罗方法是研究很广泛,以程序形式显示在图1中。

图1
图1中我们使用大写字母V表示近似值函数,因为在初始化之后,它很快就会变成一个随机变量。
对于首次使用蒙特卡罗方法和每次使用蒙特卡罗方法,当次数(或首次次数)趋于无穷时,它们都会收敛到vπ(s)。对于首次蒙特卡罗方法的情况,这一点很容易理解。在这种情况下,每次返回都是vπ(s)的独立、相同分布的估计,具有有限方差。根据大数定律,这些估计的平均值序列收敛到它们的期望值。每个平均值本身都是一个无偏估计,其误差的标准偏差为1/√n,其中n是平均值的数量。每次蒙特卡罗方法不太直观,但其估计也渐近收敛到vπ(s)(Singh和Sutton,1996)。蒙特卡罗方法的使用最好通过一个例子来说明。
三、典型例子
21点,又称黑杰克,是一种广受欢迎的赌场牌戏。游戏的目标是在不超出21点的情况下,尽可能获得高数值的牌。所有花牌都算作10点,而一张A可以算作1点或11点。我们考虑的是每个玩家独立与庄家对抗的版本。游戏开始时,庄家和玩家都会得到两张牌。庄家的一张牌是明牌,另一张是暗牌。如果玩家立即得到21点(一张A和一张10),那么就称为“自然”,除非庄家也有自然,否则玩家获胜。如果玩家没有自然,那么他可以要求额外的牌,一张一张地要(继续要牌),直到他停止(停牌)或超过21点(爆牌)。如果他爆牌,他就输了;如果他停牌,那么就轮到庄家。庄家根据固定的策略决定是否要牌或停牌,没有选择:他在任何总和为17点或更高的情况下停牌,否则就继续要牌。如果庄家爆牌,那么玩家就赢了;否则,结果(赢、输或平局)由谁的最终总和最接近21点决定。
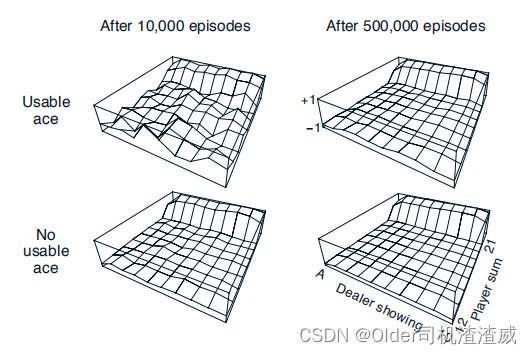
图2
图2中黑杰克策略的近似状态值函数,只在20或21点停牌,通过蒙特卡洛策略评估计算。玩二十一点被自然地制定为一段有限的MDP。 每一局二十一点是一个情节。 对于赢、输和平局,分别给予+1、-1和0的奖励。 在一局比赛中所有的奖励都是零,我们不进行贴现(γ = 1);因此这些末端奖励也是回报。 玩家的行动是击打或停牌。 状态依赖于玩家的牌和庄家的明牌。 我们假设卡片是从一个无限的套牌(即替换)中发出的,因此没有必要追踪已经发出的卡片。 如果玩家持有一张可以计为11的A牌而不会爆牌,那么这张A牌被称为可用。 在这种情况下,它总是被计为11,因为把它计为1会使总和小于或等于11,在这种情况下,没有做出决定,因为显然玩家应该一直击打。 因此,玩家根据三个变量做出决定:他当前的总和(12-21),庄家的一个明牌(A-10),以及他是否持有一张可用的A牌。 这总共有200个状态。
考虑如果在玩家总和为20或21时停牌,否则就击打的策略。 通过蒙特卡罗方法找到此策略的状态值函数,模拟许多二十一点游戏并平均每个状态后的回报。 请注意,在此任务中,相同的状态在同一情节中永远不会重复发生,因此没有首次访问和每次访问的MC方法之间的区别。 通过这种方式,我们获得了图2中所示的状态值函数的估计值。具有可用A牌的状态的估计值不太确定也不太规律,因为这些状态不太常见。 无论如何,经过50万场比赛后,价值函数被很好地逼近。
相关文章:

强化学习中蒙特卡罗方法
一、蒙特卡洛方法 这里将介绍一个学习方法和发现最优策略的方法,用于估计价值函数。与前文不同,这里我们不假设完全了解环境。蒙特卡罗方法只需要经验——来自实际或模拟与环境的交互的样本序列的状态、动作和奖励。从实际经验中学习是引人注目的&#x…...
Pytorch从零开始实战09
Pytorch从零开始实战——YOLOv5-Backbone模块实现 本系列来源于365天深度学习训练营 原作者K同学 文章目录 Pytorch从零开始实战——YOLOv5-Backbone模块实现环境准备数据集模型选择开始训练可视化模型预测总结 环境准备 本文基于Jupyter notebook,使用Python3.…...
Milvus Cloud ——Agent 的展望
Agent 的展望 目前,LLM Agent 大多是处于实验和概念验证的阶段,持续提升 Agent 的能力才能让它真正从科幻走向现实。当然,我们也可以看到,围绕 LLM Agent 的生态也已经开始逐渐丰富,大部分工作都可以归类到以下三个方面进行探索: Agent模型 AgentBench[4] 指出了不同的 L…...

EM@比例恒等式@分式恒等式
文章目录 比例恒等式(分式恒等式)分式等式链例 比例恒等式(分式恒等式) 设 a b c d \frac{a}{b}\frac{c}{d} badc(0)令这个比值为 k k k,则 a k b akb akb(0-1), c k d ckd ckd(0-2),以下恒等式在表达式有意义的情形下成立(例如分母不为0) 合比定理: a b b c d d \f…...

使用米联客FPGA开发板进行光口开发时遇到的问题总结
使用的开发板型号:米联客MA703FA, 实物图如下 FPGA型号为a35t 米联客提供的开发板资料中的FPGA型号为a100,所以要想使用开发板例程必须进行FPGA的重新选择。如下图 通过对开发板原理图的分析,例程代码不用做任何修改就可使用&am…...

【chat】 1:Ubuntu 20.04.3 编译安装moduo master分支
muduo 基于reactor反应堆模型的多线程C++网络库大佬的官方仓库有cpp17分支看了下cmakelist文件里面还是要依赖不少库,比如boost protobuf而且cpp17 似乎 是2021年的master 是2022更新的那么还是选择master吧。ubuntu版本 Ubuntu 20.04.3 root@k8s-master-2K4G:~# uname -a Lin…...
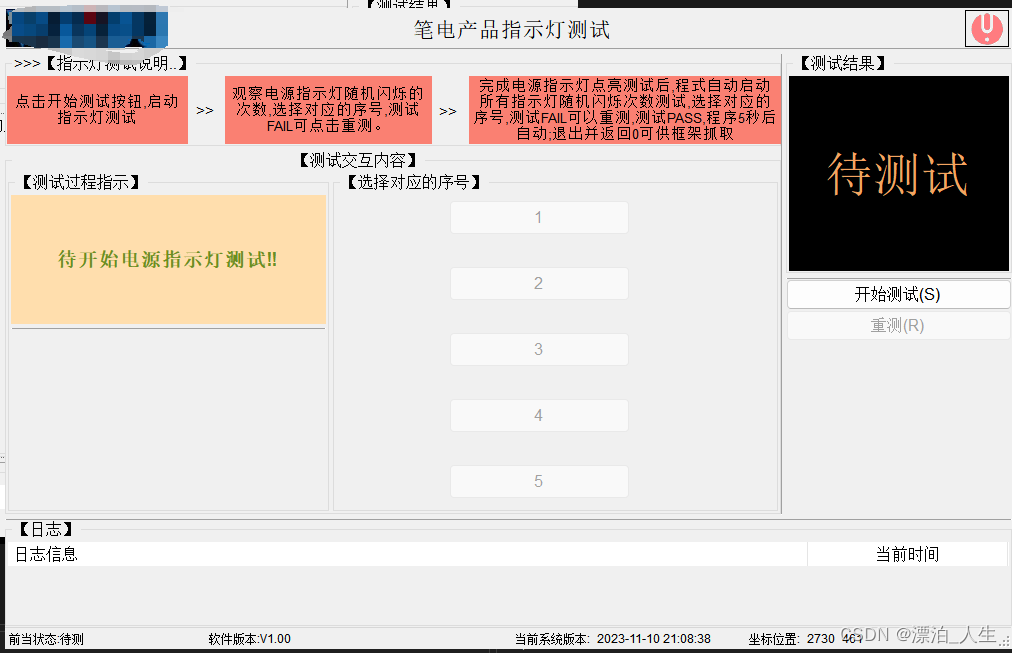
C#基于inpoutx64读写ECRAM硬件信息
inpoutx64.dll分享路径: 链接:https://pan.baidu.com/s/1rOt0xtt9EcsrFQtf7S91ag 提取码:7om1 1.InpOutManager: using System; using System.Collections.Generic; using System.Linq; using System.Runtime.InteropServi…...
图论13-最小生成树-Kruskal算法+Prim算法
文章目录 1 最小生成树2 最小生成树Kruskal算法的实现2.1 算法思想2.2 算法实现2.2.1 如果图不联通,直接返回空,该图没有mst2.2.2 获得图中的所有边,并且进行排序2.2.2.1 Edge类要实现Comparable接口,并重写compareTo方法 2.2.3 取…...
免费博客搭建笔记
title: 免费博客搭建笔记 tags: 博客搭建 本次是对自己在网上学习github搭建一个 👇个人免费静态网站的总结当然不是很完美👇 Bow to the new king iYANG (yangsongl1n.github.io) 接着我会从我的写笔记的个人习惯来逐步介绍如何搭建这个网站 1.写笔…...

网络运维Day10
文章目录 SHELL基础查看有哪些解释器使用usermod修改用户解释器BASH基本特性 shell脚本的设计与运行编写问世脚本脚本格式规范执行shell脚本方法一方法二实验 变量自定义变量环境变量位置变量案例 预定义变量 变量的扩展运用多种引号的区别双引号的应用单引号的应用反撇号或$()…...

@Cacheable 注解的 @CacheManager 示例
pom.xml 依赖包: <dependency><groupId>org.springframework.data</groupId><artifactId>spring-data-redis</artifactId></dependency><dependency><groupId>redis.clients</groupId><artifactId>jed…...

springboot二维码示例
pom.xml依赖 <dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.8.16</version></dependency><dependency><groupId>com.google.zxing</groupId><artifactId>…...

nacos做服务配置和服务器发现
一、创建项目 1、创建一个spring-boot的项目 2、创建三个模块file、system、gateway模块 3、file和system分别配置启动信息,并且创建一个简单的控制器 server.port9000 spring.application.namefile server.servlet.context-path/file4、在根目录下引入依赖 <properties&g…...

KCC@广州与 TiDB 社区联手—广州开源盛宴
10月21日,KCC广州与 TiDB 社区联手,在海珠区保利中悦广场 29 楼召开了一次难忘的开源盛宴。这不仅仅是 KCC广州的又一次线下见面,更代表着与 TiDB 社区及广州技术社区的首次深度合作。 活动的策划与组织由 KCC广州负责人 - 惠世冀、PingCAP 的…...
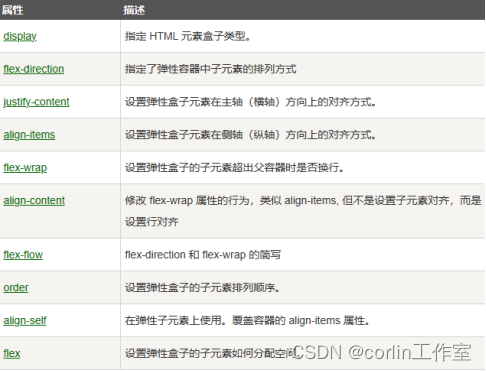
CSS3 分页、框大小、弹性盒子
一、CSS3分页: 网站有很多个页面,需要使用分页来为每个页面做导航。示例: <style> ul.pagination { display: inline-block; padding: 0; margin: 0; } ul.pagination li {display: inline;} ul.pagination li a { color: black; f…...
函数,以提取指定范围内的逐日的二氧化氮平均浓度为例)
GEE问题——GEE中循环的使用map()函数,以提取指定范围内的逐日的二氧化氮平均浓度为例
问题: 我有一个简单的代码,可以帮助计算德克萨斯州每个县的对流层二氧化氮平均浓度。目前,我可以将其导出为我指定的任何日期范围的 csv 表,但我想 1) 提取每天平均值,例如 3 个月(2020 年 3 月至 2020 年 5 月,约 90 天)--手动多次运行肯定不是办法,而且我的编码技…...

短信验证码实现(阿里云)
如果实现短信验证,上教程,这里用的阿里云短信服务 短信服务 (aliyun.com) 进入短信服务后开通就行,可以体验100条免费,刚好测试用 这里由自定义和专用,测试的话就选择专用吧,自定义要审核, Se…...

如何对element弹窗进行二次封装
方式一使用$refs 个人比较喜欢用这种的 通过$refs打开的同时 还能给弹窗组件传参 一些框架使用的也是这种方式 父组件 <template><div><el-button type"text" click"handleDialogOpen">打开嵌套表单的 Dialog</el-button><Dia…...
【微服务专题】手写模拟SpringBoot
目录 前言阅读对象阅读导航前置知识笔记正文一、工程项目准备1.1 新建项目1.1 pom.xml1.2 业务模拟 二、模拟SpringBoot启动:好戏开场2.1 启动配置类2.1.1 shen-base-springboot新增2.1.2 shen-example客户端新增启动类 三、run方法的实现3.1 步骤一:启动…...
七个优秀微服务跟踪工具
随着微服务架构复杂性的增加,在问题出现时确定问题的根本原因变得更具挑战性。日志和指标为我们提供了有用的信息,但并不能提供系统的完整概况。这就是跟踪的用武之地。通过跟踪,开发人员可以监控微服务之间的请求进度,从而使他们…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
