C++算法:矩阵中的最长递增路径
涉及知识点
拓扑排序
题目
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:
输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
示例 2:
输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3:
输入:matrix = [[1]]
输出:1
参数范围:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 231 - 1
2023年一月版
class Solution {
public:
int longestIncreasingPath(vector<vector>& matrix) {
m_r = matrix.size();
m_c = matrix[0].size();
m_dp.assign(m_r, vector(m_c, -1));
std::map<int,vector<pair<int,int>>> mVRC;
for (int r = 0; r < m_r; r++)
{
for (int c = 0; c < m_c; c++)
{
mVRC[matrix[r][c]].emplace_back(r, c);
}
}
for (auto& it : mVRC)
{
for (auto& rc : it.second)
{
m_dp[rc.first][rc.second] = Test(matrix, rc.first, rc.second);
}
}
int iMax = 0;
for (int r = 0; r < m_r; r++)
{
for (int c = 0; c < m_c; c++)
{
iMax = max(iMax, m_dp[r][c]);
}
}
return iMax;
}
int Test(const vector<vector>& matrix,int r, int c)
{
int iMax = 0;
if ((r > 0) && (matrix[r][c] > matrix[r - 1][c]))
{
iMax = max(iMax,m_dp[r-1][c] );
}
if ((r +1 < m_r ) && (matrix[r][c] > matrix[r + 1][c]))
{
iMax = max(iMax, m_dp[r + 1][c]);
}
if ((c > 0) && (matrix[r][c] > matrix[r][c-1]))
{
iMax = max(iMax, m_dp[r][c-1]);
}
if ((c + 1 < m_c) && (matrix[r][c] > matrix[r][c + 1]))
{
iMax = max(iMax, m_dp[r][c + 1]);
}
return iMax + 1;
}
int m_r;
int m_c;
vector<vector> m_dp;
};
2023年8月版
class Solution {
public:
int longestIncreasingPath(vector<vector>& matrix) {
m_r = matrix.size();
m_c = matrix.front().size();
m_iMaskNum = m_r * m_c;
//生成邻接表
vector<vector> vNeiBo(m_iMaskNum);
vector vInDeg(m_iMaskNum);
for (int r = 0; r < m_r; r++)
{
for (int c = 0; c < m_c; c++)
{
auto Add = [this,&matrix, &vNeiBo,&vInDeg](int curMask, int curValue, int r, int c)
{
if ((r < 0) || (r >= m_r))
{
return;
}
if ((c < 0) || (c >= m_c))
{
return;
}
if (curValue > matrix[r][c])
{
vNeiBo[r * m_c + c].emplace_back(curMask);
vInDeg[curMask]++;
}
};
Add(r * m_c + c, matrix[r][c], r + 1, c);
Add(r * m_c + c, matrix[r][c], r - 1, c);
Add(r * m_c + c, matrix[r][c], r, c + 1);
Add(r * m_c + c, matrix[r][c], r, c - 1);
}
}
//top排序
queue que;
vector vLen(m_iMaskNum, 0);
for (int i = 0; i < m_iMaskNum; i++)
{
if (0 == vInDeg[i])
{
que.emplace(i);
vLen[i] = 1;
}
}
while (que.size())
{
const int cur = que.front();
que.pop();
for (const auto& next : vNeiBo[cur])
{
if (–vInDeg[next] == 0)
{
vLen[next] = vLen[cur] + 1;
que.emplace(next);
}
}
}
return *std::max_element(vLen.begin(), vLen.end());
}
int m_r;
int m_c;
int m_iMaskNum;
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 洒家想对大家说的话
|
|-|
|闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。|
| 墨家名称的来源:有所得以墨记之。 |
|如果程序是一条龙,那算法就是他的是睛|
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境:
VS2022 C++17

相关文章:

C++算法:矩阵中的最长递增路径
涉及知识点 拓扑排序 题目 给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。 对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允…...
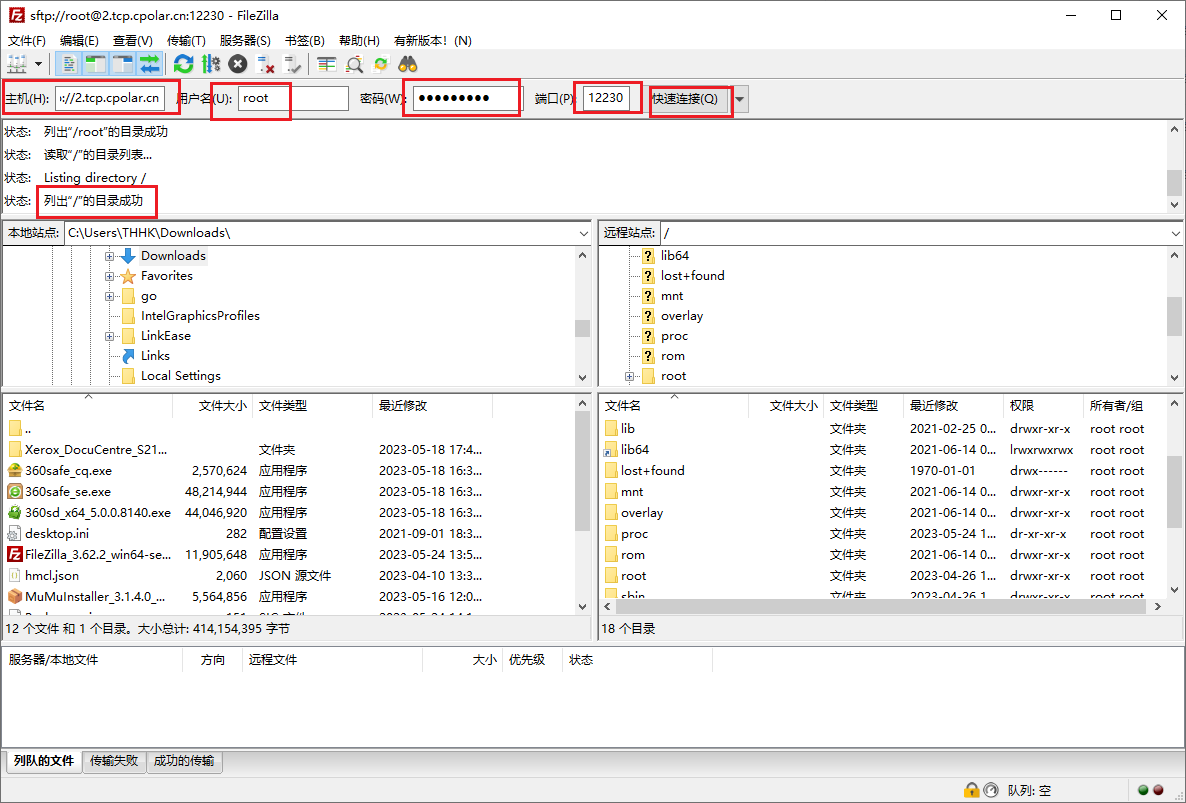
OpenWRT配置SFTP远程文件传输,让数据分享更安全
文章目录 前言 1. openssh-sftp-server 安装2. 安装cpolar工具3.配置SFTP远程访问4.固定远程连接地址 前言 本次教程我们将在OpenWRT上安装SFTP服务,并结合cpolar内网穿透,创建安全隧道映射22端口,实现在公网环境下远程OpenWRT SFTP…...

已解决:rm: 无法删除“/opt/module/zookeeper-3.4.10/zkData/zookeeper_server.pid“: 权限不够
解决: ZooKeeper JMX enabled by default Using config: /opt/module/zookeeper-3.4.10/bin/../conf/zoo.cfg Stopping zookeeper ... /opt/module/zookeeper-3.4.10/bin/zkServer.sh: 第 182 行:kill: (4149) - 不允许的操作 rm: 无法删除"/opt/module/zooke…...
【DataStream API - Source算子】)
Flink(四)【DataStream API - Source算子】
前言 今天开始学习 DataStream 的 API ,这一块是 Flink 的核心部分,我们不去学习 DataSet 的 API 了,因为从 Flink 12 开始已经实现了流批一体, DataSet 已然是被抛弃了。忘记提了,从这里开始,我开始换用 F…...
GIS入门,xyz地图瓦片是什么,xyz数据格式详解,如何发布离线XYZ瓦片到nginx或者tomcat中
XYZ介绍 XYZ瓦片是一种在线地图数据格式,由goole公司开发。 与其他瓦片地图类似,XYZ瓦片将地图数据分解为一系列小的图像块,以提高地图显示效率和性能。 XYZ瓦片提供了一种开放的地图平台,使开发者可以轻松地将地图集成到自己的应用程序中。同时,它还提供了高分辨率图像和…...
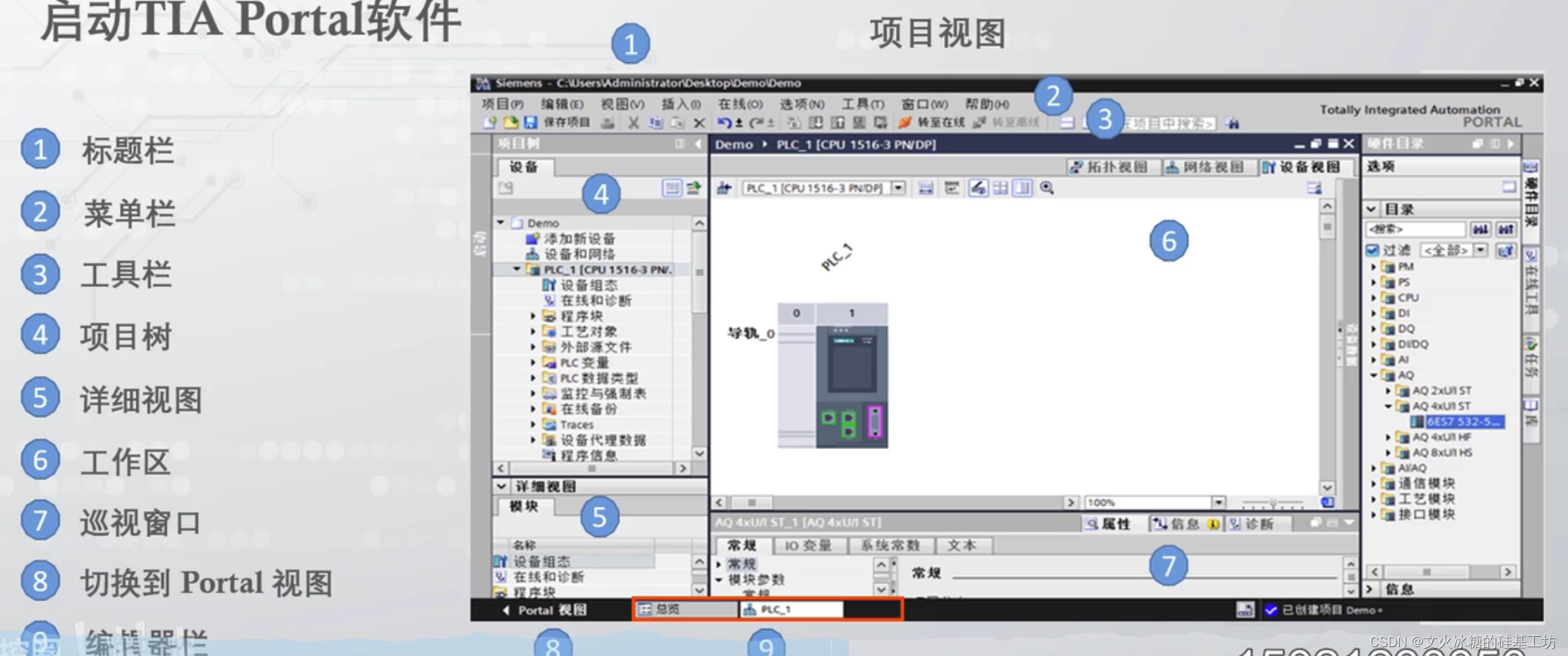
[工业自动化-14]:西门子S7-15xxx编程 - 软件编程 - STEP7 TIA博途是全集成自动化软件TIA portal快速入门
目录 一、TIA博途是全集成自动化软件TIA portal快速入门 1.1 简介 1.2 软件常用界面 1.3 软件安装的电脑硬件要求 1.4 入口 1.5 主界面 二、PLC软件编程包含哪些内容 2.1 概述 2.2 电机运动控制 一、TIA博途是全集成自动化软件TIA portal快速入门 1.1 简介 Siemens …...

【教3妹学编程-算法题】Range 模块
3妹:哈哈哈哈哈哈哈哈 2哥 : 3妹看什么呢,笑的这么开森 3妹:2哥你快来看啊,成都欢乐谷的NPC模仿“唐僧”, 太搞笑了。 2哥 : 哦这个我也看到了,真的是唯妙唯肖,不能说像,只能说一模一…...

SpringBoot+MybatisPlus Restful示例
增删改查,分页 CREATE TABLE tbl_book ( id int NOT NULL AUTO_INCREMENT, type varchar(20) CHARACTER SET utf8 COLLATE utf8_general_ci DEFAULT NULL, name varchar(50) CHARACTER SET utf8 COLLATE utf8_general_ci DEFAULT NULL, desc_ription varchar(255) CHAR…...

【数据结构】树与二叉树(十一):二叉树的层次遍历(算法LevelOrder)
文章目录 5.2.1 二叉树二叉树性质引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。引理5.2:高度为k的二叉树中至多有 2 k 1 − 1 2^{k1}-1 2k1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。引理5.3&…...
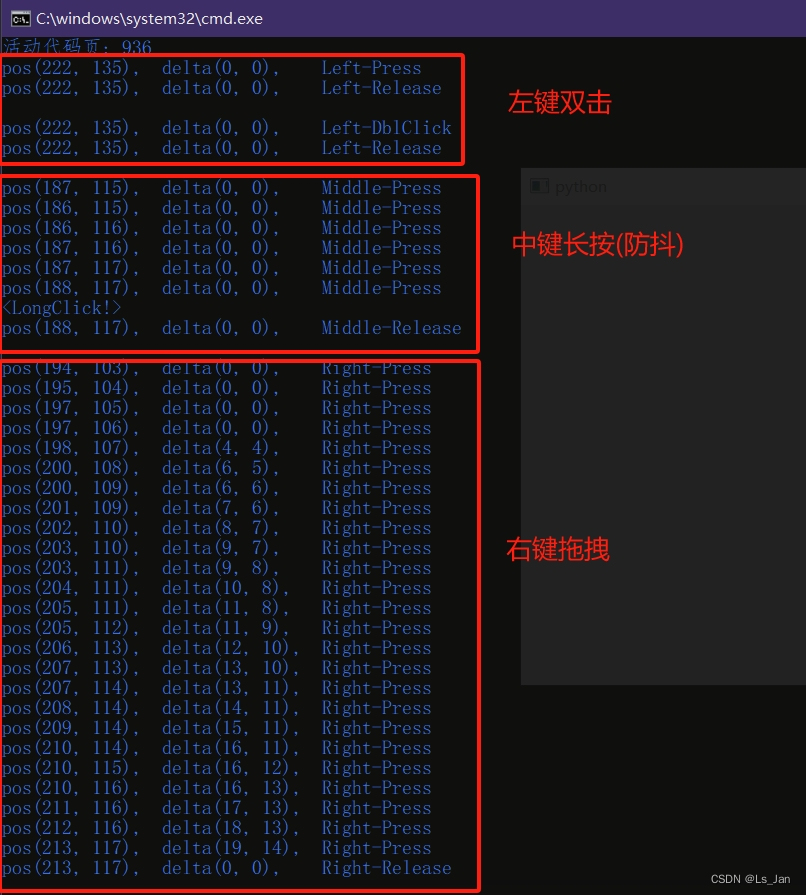
【PyQt】(自制类)处理鼠标点击逻辑
写了个自认为还算不错的类,用于简化mousePressEvent、mouseMoveEvent和mouseReleaseEvent中的鼠标信息。 功能有以下几点: 鼠标当前状态,包括鼠标左/中/右键和单击/双击/抬起鼠标防抖(仅超出一定程度时才判断鼠标发生了移动),灵…...
JAVA IDEA 下载
超简单步骤一: IntelliJ IDEA 官方下载链接 点击以上链接进入下图,点击下载 继续点下载,然后等待下载完后打开安装包即可 步骤二: 打开下好的安装包,点击Browse...我们把它下载到自己喜欢的地方(主要是别占…...

DevOps简介
DevOps简介 1、DevOps的起源2、什么是DevOps3、DevOps的发展现状4、DevOps与虚拟化、容器 1、DevOps的起源 上个世纪40年代,世界上第一台计算机诞生。计算机离不开程序(Program)驱动,而负责编写程序的人,被称为程序员&…...

体验前所未有的显示器管理体验:BetterDisplay Pro Mac
在现代的数字化时代,显示器是我们日常生活和工作中不可或缺的一部分。从笔记本电脑到台式机,从平板电脑到手机,几乎所有的电子设备都配备了显示器。然而,对于专业人士和从事设计行业的人来说,仅仅依靠系统自带的显示器…...

python用pyinstaller打包exe,去掉黑窗口
使用Python编写程序将Python脚本打包成可执行文件(EXE),但是会有一个命令框产生,很烦,所以,去掉这个框 1,安装pyinstaller pip install pyinstaller2,打包产生cmd命令框 pyinstaller --onefi…...
如何关闭Windows Defender(亲测可行!!非常简单)
一、背景 Windows Defender(简称WD)真的太讨厌了,经常给你报你下载的文件是病毒,且不说真的是不是病毒,它都不询问直接删。 另外聚资料显示WD还会不合时宜地执行扫描导致系统变慢(不会在合适的、空闲的时…...

【objectarx.net】创建多重引线
创建多重引线...

【objectarx.net】创建组,列出所有组,查找实体所在的组
创建组,列出所有组...

Llama2通过llama.cpp模型量化 WindowsLinux本地部署
Llama2通过llama.cpp模型量化 Windows&Linux本地部署 什么是LLaMA 1 and 2 LLaMA,它是一组基础语言模型,参数范围从7B到65B。在数万亿的tokens上训练的模型,并表明可以专门使用公开可用的数据集来训练最先进的模型,而无需求…...
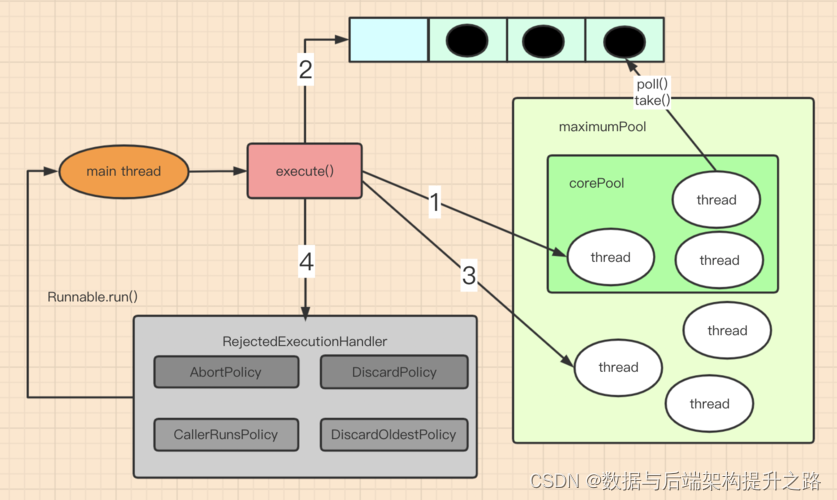
Coding面试题之手写线程池
原理图 JDK线程池原理 实现代码 1.线程类(PoolThread) 这个类用于执行任务队列中的任务。 public class PoolThread extends Thread {private final Queue<Runnable> taskQueue;private boolean isStopped false;private long lastTaskTime …...

【objectarx.net】删除零长度曲线和获取零长度曲线的数量
删除零长度曲线和获取零长度曲线的数量...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
