环形链表解析(c语言)c语言版本!自我解析(看了必会)
目录
1.判断一个表是否是环形链表!
代码如下
解析如下
2.快指针的步数和慢指针的步数有什么影响(无图解析)
3.怎么找到环形链表的入环点
代码如下
解析如下
1.判断一个表是否是环形链表!
代码如下
bool hasCycle(struct ListNode *head) {struct ListNode* fast = head;struct ListNode* slow = head;while(fast && fast->next){fast = fast->next->next;slow = slow->next;if(fast == slow){return true;}}return false;
}解析如下
快慢指针就是一个指针一次走好几个节点,而一个指针一次走少一点。字面意思
这里采用的是一个走两节点,一个走一个节点。
为什么要用快慢指针呢?
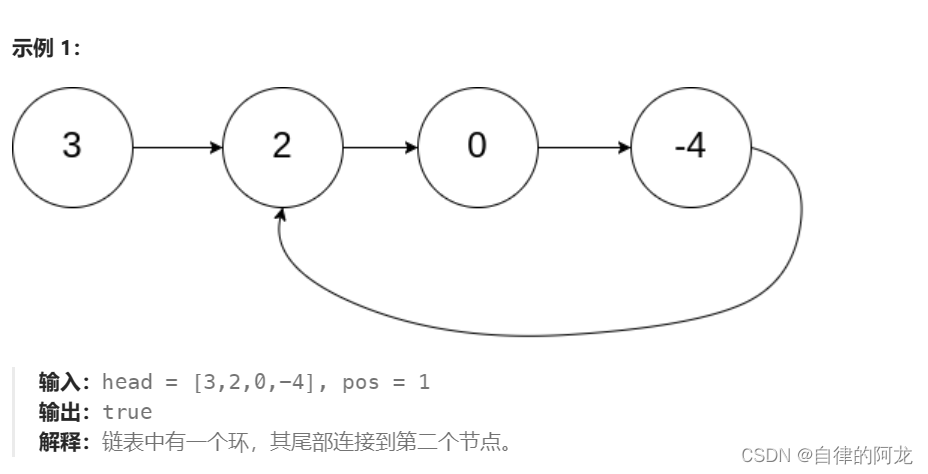
这个图是本题的原图,你可以用一个手指当做快指针,一个手指当做慢指针 。最终两个手指会相遇。这就是最普遍的快慢指针,fast走的是slow的路程的两倍,这就是相当于一个追击问题,再跑1000米的时候,你的好朋友的配速是你的两倍,最终他会超你一圈一个道理。
2.快指针的步数和慢指针的步数有什么影响(无图解析)
根据上面的判断,那这两个指针一定会相遇吗?
思考如果快指针一次走三,慢指针一次走一,那他们两还会相遇吗?
如果快指针走N慢指针走M呢?
其实上面第一题 一个走两步一个走一步的方法是有一个公式的。

就以这个为例,当slow走到2的时候,fast已经走到-4,那他两距离相差1,下一次fast和slow必定相遇,因为两人每次走的距离差为1,把slow入环时两者的距离记作N,因为两者的距离差为1,N-1-1-1-1-1......N总有被减到0的时候,减到0那两者就是在一个位置,就相遇了。
那如果一个走三步的情况和一个走一步的情况呢?
这个也很好解释,假设在slow进入环的时候,fast和slow的距离为N,头结点到slow的距离为L,环的大小为C

如果一个走三步一个走一步那两者的每次的距离差就是2.现在要让fast去追这个slow。
两者差距为N。如果每次都减2,如果N为偶数的话,那还好最终会减到0,
如果N为奇数的话最终(除了1)最终可能会减为-1,就是fast 直接超过 slow。
那最后会不会相遇呢?现在两者的距离就变成C-1了,如果C-1为偶数那接下来两个人就会碰到,
如果为奇数,那就不行了两人会再次错过吗?其实不然
假设slow 进环时总的距离是L,期间fast就走了L+n * C - N(小n是fast走的圈数,随机值)
因为fast最终走的距离是slow 的三倍,最终可以列出等式 3L = L + n * C - N
最终 2L = n * c - N . 因为两者不相遇是因为 N 为奇数,所以N为奇数 ,2L一定是偶数。
那n * c 总的来说也必须是一个奇数,因为等式一个奇数减偶数才能等于一个偶数。
所以 c 是奇数 ,c -1 就是偶数。那说明两者不会一直不相等。最终可能会相遇。
3.怎么找到环形链表的入环点
代码如下
struct ListNode *detectCycle(struct ListNode *head) {struct ListNode* fast = head,*slow = head;while(fast && fast->next){fast = fast->next->next;slow = slow->next;if(fast == slow){struct ListNode* cur = slow;while(cur != head){cur = cur->next;head = head->next;}return head;}}return NULL;}解析如下
首先做这题前,我们需要画一个图
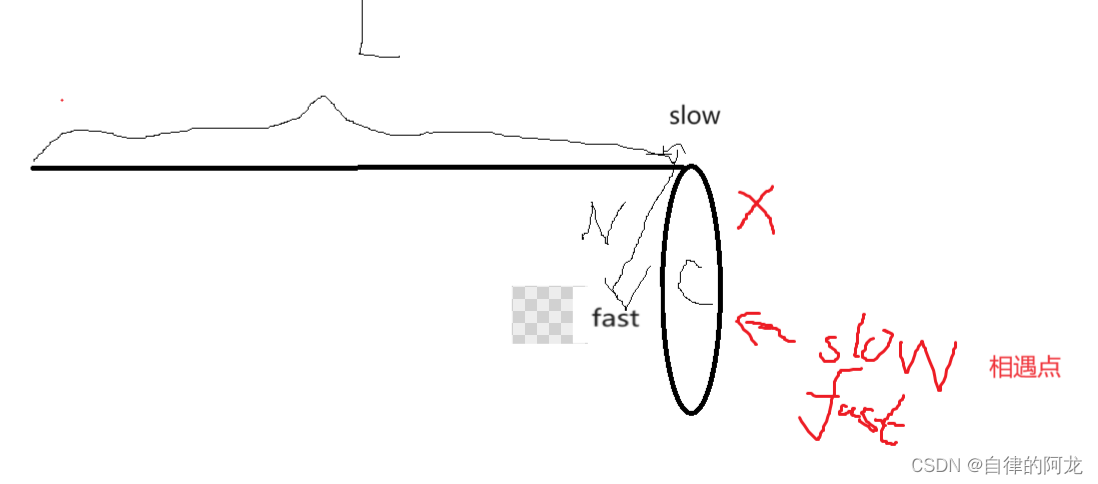
同样假设入环点到头结点的距离为L,两者相遇的距离为X,环的大小为C
首先在slow 在入环点的时候,fast 走了 L + C * n - N 。
在slow 入环后 两者在 X 距离后相遇。
之后slow 所走的路程就变为了 L + X,fast 走的路程就是 L + n * C + X。
因为fast的路程等于slow 的两倍,所以就可以列出等式,2*(L+X) = L + n * C + X.
解出答案后等于 L = n * C - X。这个答案的意义是什么呢?
就是L的距离等于这么fast走的这么多圈后减掉 X的距离。就是L 加上 slow 多走的环的距离,就是 fast 之前走过多少圈的环。那接下来就可以知道,其实我们可以用头指针(头结点)和慢指针的位置,每人都每次都向后走一步,最后两者就会在入环点相遇。
因为L = n * C - X,所以只要让两者相遇的点作为起点,然后向后走n 圈后,就等于L ,所以一个指针从头开始走,一个指针从 相遇点开始走,两者最终会在相遇点L 相遇。
相关文章:

环形链表解析(c语言)c语言版本!自我解析(看了必会)
目录 1.判断一个表是否是环形链表! 代码如下 解析如下 2.快指针的步数和慢指针的步数有什么影响(无图解析) 3.怎么找到环形链表的入环点 代码如下 解析如下 1.判断一个表是否是环形链表! 代码如下 bool hasCycle(struct L…...

科技云报道:数智化升级,如何跨越数字世界与实体产业的鸿沟?
科技云报道原创。 数智化是当下商业环境下最大的确定性。 2022年,中国数字经济规模达50.2万亿元,占国内生产总值比重提升至41.5%,数字经济成为推动经济发展的重要引擎。从小型创业公司到跨国巨头,数字化转型在企业发展历程中彰显…...
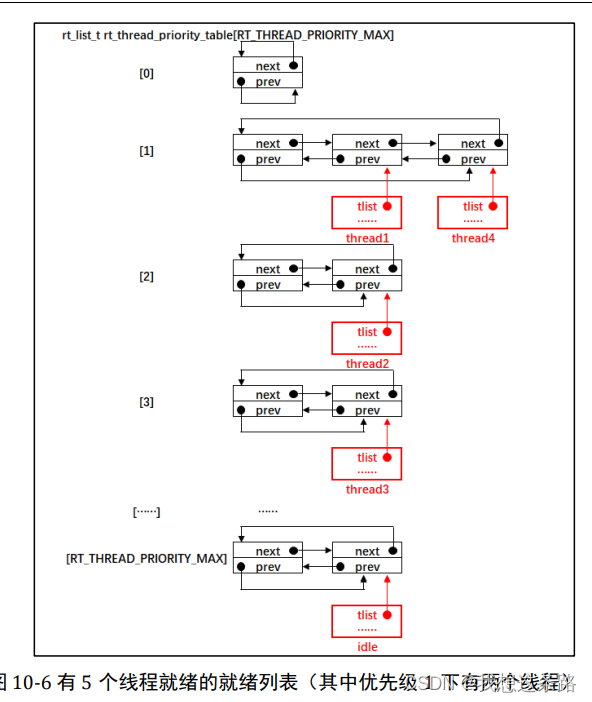
Rt-Thread 移植6--多线程(KF32)
6.1 就绪列表 6.1.1 线程就绪优先级组 线程优先级表的索引对应的线程的优先级。 为了快速的找到线程在线程优先级表的插入和移出的位置,RT-Thread专门设计了一个线程就绪优先级组。线程就绪优先组是一个32位的整型数,每一个位对应一个优先级ÿ…...

HarmonyOS应用开发-首选项与后台通知管理
首选项 在移动互联网蓬勃发展的今天,移动应用给我们生活带来了极大的便利,这些便利的本质在于数据的互联互通。因此在应用的开发中数据存储占据了非常重要的位置,HarmonyOS应用开发也不例外。本章以HarmonyOS的首选项为例,介绍了…...
通过easyexcel导出数据到excel表格
这篇文章简单介绍一下怎么通过easyexcel做数据的导出,使用之前easyui构建的歌曲列表crud应用,添加一个导出按钮,点击的时候直接连接后端接口地址,在后端的接口完成数据的导出功能。 前端页面完整代码 let editingId; let request…...
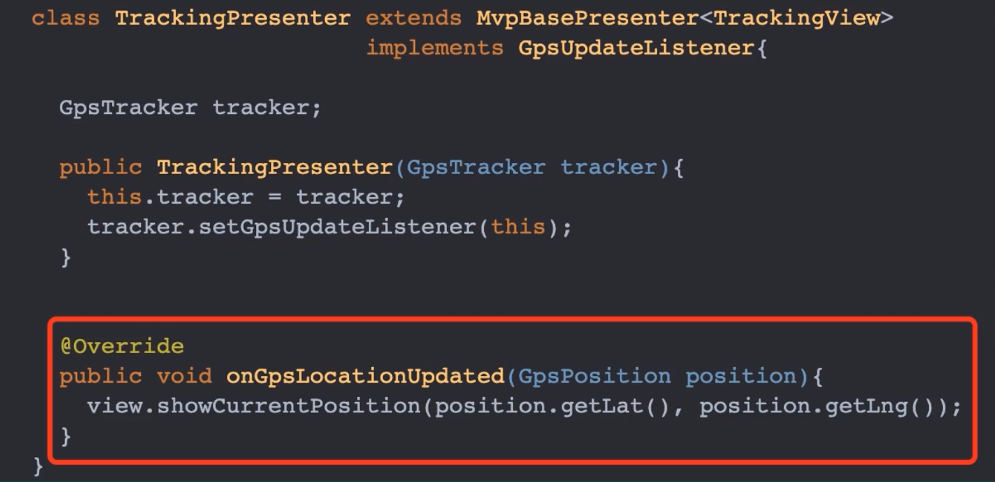
Android---MVP 中 presenter 声明周期的管理
我们经常在 Android MVP 架构中的 Presenter 层做一些耗时操作,比如请求网络数据,然后根据请求后的结果刷新 View。但是,如果按返回结束 Activity,而 Presenter 依然在执行耗时操作。那么就有可能造成内存泄漏,严重时甚…...

Oracle中的索引碎片
索引碎片是指索引在存储空间上不连续的分布情况,它可能会影响到数据库性能和查询效率。索引碎片化主要由以下几个原因导致: 插入、更新和删除操作:当对表中的数据进行插入、更新或删除操作时,索引也需要相应地更新。这些DML操作可…...
Java必刷入门递归题×5(内附详细递归解析图)
目录 1.求N的阶乘 2.求12...N的和 3.顺序打印数字的每一位 4.求数字的每一位之和 5.求斐波拉契数列 1.求N的阶乘 (1)解析题目意思 比如求5的阶乘,符号表示就是5!;所以5!5*4*3*2*1我们下面使用简单的…...

android 闪屏图适配尺寸
不同的 Android 设备可能具有不同的屏幕尺寸和分辨率,因此最好提供不同尺寸的启动画面图像,以确保与各种设备的兼容性。 以下是 Android 启动画面图像的一些最常见尺寸: 320 x 480像素(肖像) 480 x 320像素࿰…...
与(?m)的区别)
正则表达式中(?s)与(?m)的区别
理论: (?m) 和 (?s) 是正则表达式中的两个模式标志,它们具有不同的作用: (?m) 多行模式标志(也称为 “multiline” 模式): 默认情况下,正则表达式将整个输入字符串视为单行多行文本中使用…...

Clickhouse学习笔记(11)—— 数据一致性
使用合并树引擎时,无论是ReplacingMergeTree还是SummingMergeTree,都只能保证数据的最终一致性,因为数据的去重、聚合等操作会在数据合并的期间进行,而合并会在后台以一个不确定的时间进行,因此无法预先计划࿱…...

【uniapp】六格验证码输入框实现
效果图 代码实现 <view><view class"tips">已发送验证码至<text class"tips-phone">{{ phoneNumber }}</text></view><view class"code-input-wrap"><input class"code-input" v-model"…...

【react hook】在react hook组件中,使用Antd Table组件,columns数据异步获取,list数据更新但没有rerender解决办法
情景描述 我们有一个react组件,显示了一个Antd Table组件,设置了一个columns变量并复制给Table的columns属性,由于我们请求的datasource来源是异步的,示例伪代码如下: const [columns, setColumns] useState([]); /…...
ChatGPT的图识别来了
前几天ChatGPT推出了Dall-E 3功能,可以根据文字和描述一段话来生成一个或者一组图。 这次又来重磅了,图识别又来了!换句话说,也即是文生图,图生文都可以实现了,一起来试试 1、解释图中的意思 ࿰…...

java Stream编程笔记
文章目录 Stream介绍什么是 Stream? Stream中间操作过滤操作(filter)映射操作(map)排序操作(sorted)截断操作(limit 和 skip) Stream 的终止操作forEach 和 peek聚合操作…...

顶顶通语音识别使用说明
介绍 顶顶通语音识别软件(asrproxy)是一个对接了多种语音识别接口的语音识别系统。可私有化部署(支持中文英文和方言等,支持一句话识别、实时流识别、多声道录音文件识别。 原理 asrproxy内嵌了阿里达摩院的开源语音识别工具包FunASR,后续我们也会使用自有的预料…...
重磅发布 OpenAI 推出用户自定义版 ChatGPT
文章目录 重磅发布 OpenAI 推出用户自定义版 ChatGPT个人简介 重磅发布 OpenAI 推出用户自定义版 ChatGPT OpenAI 首届开发者大会 (OpenAI DevDay) 于北京时间 11 月 7 日凌晨 02:00 开始,大会上宣布了一系列平台更新。其中一个重要更新是用户可以创建他们自己的自定…...
读取 json 文件)
Java 幼儿园(20231111)读取 json 文件
1、功能场景 (1)多人合作开发一个功能模块时,需要调用外部接口 (2)对方接口的开发工作还没有完成,只能提供一个返回值的示例文件 json 文件。 (3)返回的 json 数据多达几百个字段。 …...
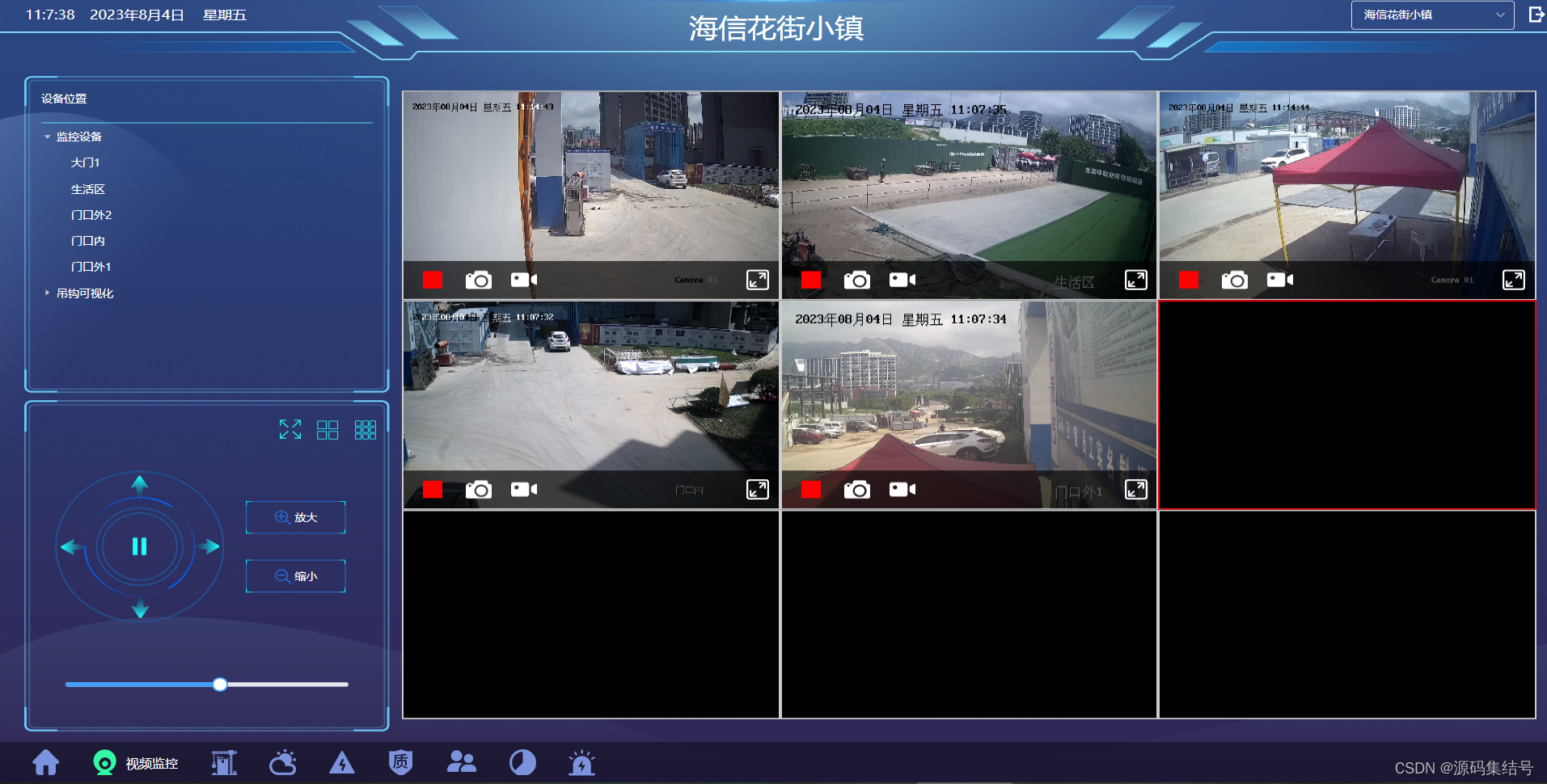
云计算、大数据技术的智慧工地,实现对建筑工地实时监测、管理和控制的一种新型建筑管理方式
智慧工地是利用物联网、云计算、大数据等技术,实现对建筑工地实时监测、管理和控制的一种新型建筑管理方式。 智慧工地架构: 1、终端层: 充分利用物联网技术、移动应用、智能硬件设备提高现场管控能力。通过RFID、传感器、摄像头、手机等终…...

功能案例 -- 通过开关,改变白天和黑夜
效果展示 代码展示 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><style>:root {--default-bac-color: #f…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
