[LeetCode周赛复盘] 第 371 场周赛20231112
[LeetCode周赛复盘] 第 371 场周赛20231112
- 一、本周周赛总结
- 100120. 找出强数对的最大异或值 I
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 100128. 高访问员工
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 100117. 最大化数组末位元素的最少操作次数
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 100124. 找出强数对的最大异或值 II
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 参考链接
一、本周周赛总结
- T1 模拟。
- T2 模拟。
- T3 模拟贪心。
- T4 带删除的异或字典树+滑窗。
100120. 找出强数对的最大异或值 I
100120. 找出强数对的最大异或值 I
1. 题目描述
和T4相同,略。
2. 思路分析
看T4。
3. 代码实现
略。
100128. 高访问员工
100128. 高访问员工
1. 题目描述
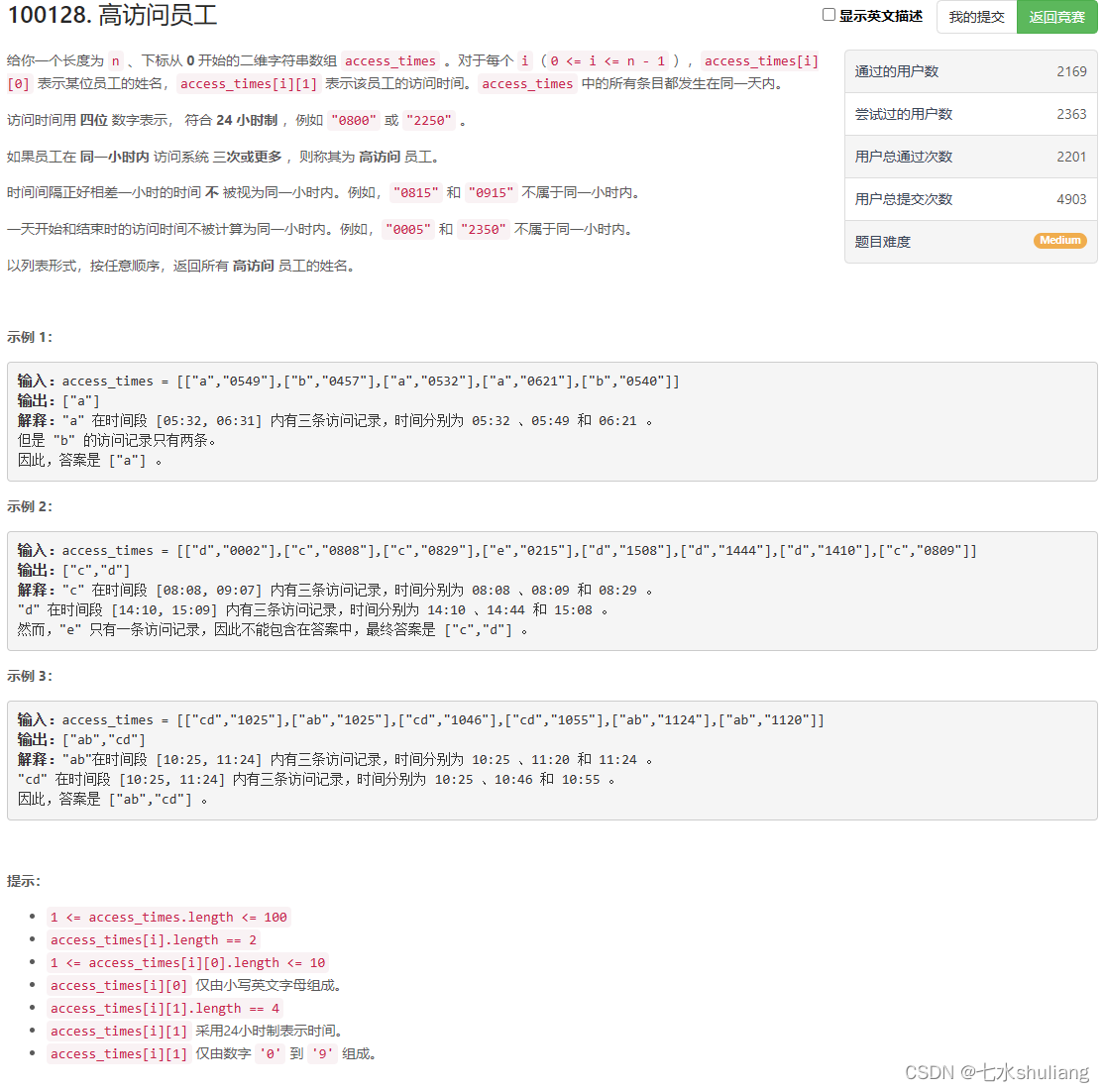
2. 思路分析
- 把时间转化成分钟数,看a[i]-a[i-2]<60即可。
3. 代码实现
class Solution:def findHighAccessEmployees(self, access_times: List[List[str]]) -> List[str]:g = defaultdict(list)for x,y in access_times:g[x].append(y)ans = []def f(x):return int(x[:2])*60 + int(x[2:])for p, a in g.items():a = sorted(f(x) for x in a)for i in range(2,len(a)):if a[i] - a[i-2] < 60:ans.append(p)breakreturn ans
100117. 最大化数组末位元素的最少操作次数
100117. 最大化数组末位元素的最少操作次数
1. 题目描述
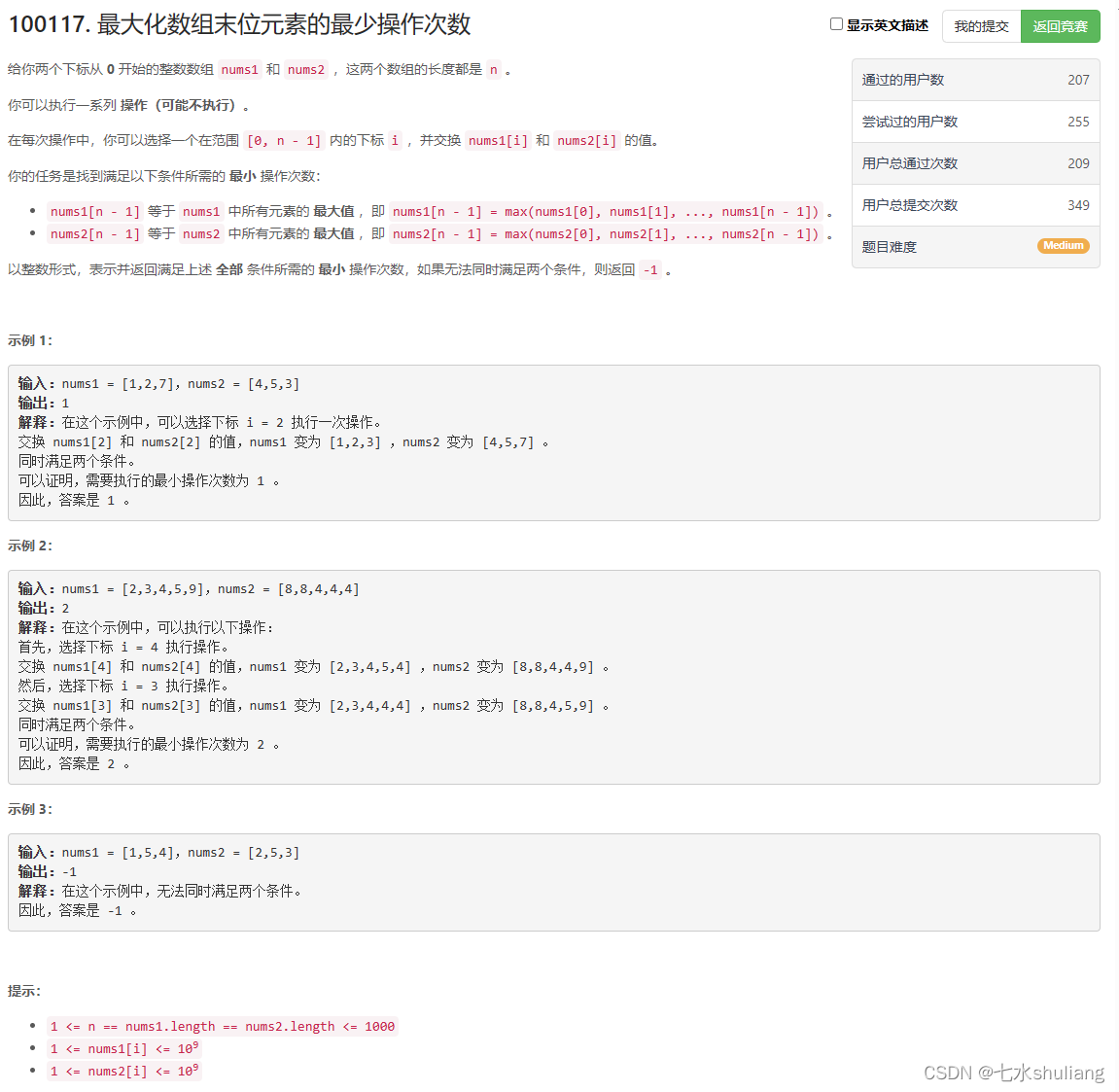
2. 思路分析
- 由于每次操作只能交换同位置的数,那我们尝试末尾是否交换,然后枚举每个位置是否交换即可。
3. 代码实现
class Solution:def minOperations(self, nums1: List[int], nums2: List[int]) -> int:n = len(nums1)def f(e1,e2):ans = 0if not (e1 == nums1[-1] and e2 == nums2[-1]):ans = 1 for x,y in zip(nums1[:-1], nums2[:-1]):if x <= e1 and y <= e2:continuex,y = y,x if x <= e1 and y <= e2:ans += 1else:return inf return ans ans = min(f(nums1[-1],nums2[-1]),f(nums2[-1],nums1[-1]))if ans == inf:return -1 return ans
100124. 找出强数对的最大异或值 II
100124. 找出强数对的最大异或值 II
1. 题目描述
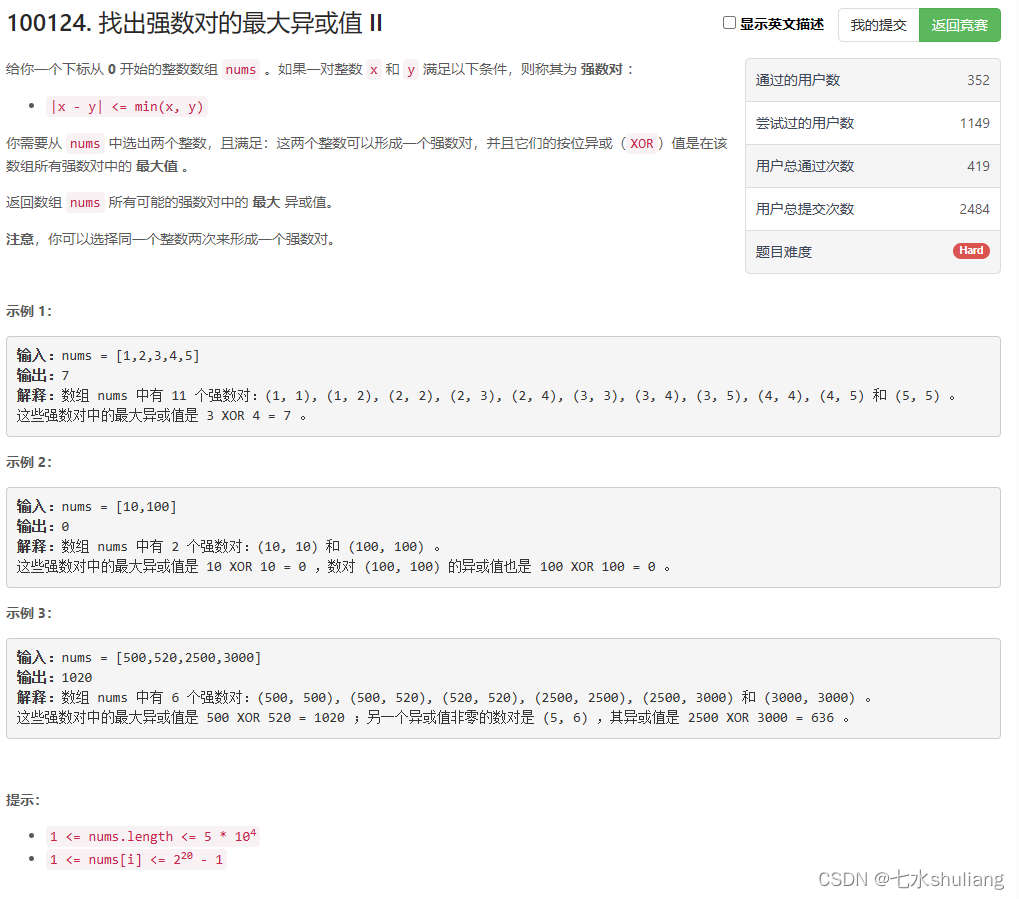
2. 思路分析
T1的数据强化版。
- 公式可以转化,令x>=y,则|x-y|<=min(x,y)等价于
x-y <= y,即x<=2y
- 我们把数组排序,然后滑窗处理,对于每个入窗的x,队头<x/2的数据都移除,那么窗口内的数据都是合法的y。
- 如何对窗口内的数据全部异或x去最大值呢?这可以用TrieXOR来处理复杂度lg(U)。
- 注意由于要出窗,字典树要支持删除。
3. 代码实现
class Solution:def maximumStrongPairXor(self, nums: List[int]) -> int:nums.sort()trie = {}def insert(v):cur = triefor i in range(20,-1,-1):p = v >> i & 1if p not in cur:cur[p] = {}cur = cur[p]cur[3] = cur.get(3,0) + 1def remove(v):cur = trie for i in range(20,-1,-1):p = v >> i & 1cur[p][3] -= 1if not cur[p][3]:del cur[p]breakcur = cur[p]def find(v):cur = trie ans = 0 for i in range(20,-1,-1):p = v>>i&1if p ^ 1 in cur:cur = cur[p^1]ans = ans << 1 | 1else:cur = cur[p]ans <<= 1return ansq = deque()ans = 0for v in nums:q.append(v)insert(v)while q[0]*2 < v: remove(q.popleft())ans = max(ans, find(v))return ans
参考链接
相关文章:

[LeetCode周赛复盘] 第 371 场周赛20231112
[LeetCode周赛复盘] 第 371 场周赛20231112 一、本周周赛总结100120. 找出强数对的最大异或值 I1. 题目描述2. 思路分析3. 代码实现 100128. 高访问员工1. 题目描述2. 思路分析3. 代码实现 100117. 最大化数组末位元素的最少操作次数1. 题目描述2. 思路分析3. 代码实现 100124…...

Google Guava Cache LoadingCache 基本使用
一. 添加依赖 <dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>27.1-jre</version> </dependency>二. 创建CacheLoader LoadingCache<Long, String> cache CacheBuilder.newB…...
AWS云服务器EC2实例进行操作系统迁移
AWS云服务器EC2实例进行操作系统迁移 文章目录 AWS云服务器EC2实例进行操作系统迁移1. 亚马逊EC2云服务器简介1.2 亚马逊EC2云务器与弹性云服务器区别 2. 亚马逊EC2云服务器配置流程2.1 亚马逊EC2云服务器实例配置2.1.1 EC2实例购买教程2.1.1 EC2实例初始化配置2.1.2 远程登录E…...
《015.SpringBoot+vue之音乐网》【前后端分离】
《015.SpringBootvue之音乐网》【前后端分离】 项目简介 [1]本系统涉及到的技术主要如下: 推荐环境配置:DEA jdk1.8 Maven MySQL 前后端分离; 后台:SpringBootMybatisMySQL; 前台:Vue3.0 TypeScript Vue-Router Vuex Axios …...

网格算法和穷举法
介绍 网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具 当需要在多个离散的点(比如网格点)…...

【AI】自回归 (AR) 模型使预测和深度学习变得简单
自回归 (AR) 模型是统计和时间序列模型,用于根据数据点的先前值进行分析和预测。这些模型广泛应用于各个领域,包括经济、金融、信号处理和自然语言处理。 自回归模型假设给定时间变量的值与其过去的值线性相关,这使得它们可用于建模和预测时…...
)
安卓常见设计模式14------单例模式(Kotlin版)
1. W1 是什么,什么是单例模式? 单例模式属于创建型模式,旨在确保一个类只有一个实例,并提供一个全局访问点来获取该实例。单例模式的核心思想是限制类的实例化,使得系统中只有一个共享的实例。 2. W2 为什么&#…...
一维卡尔曼滤波编程实践)
卡尔曼家族从零解剖-(06)一维卡尔曼滤波编程实践
讲解关于slam一系列文章汇总链接:史上最全slam从零开始,针对于本栏目讲解的 卡尔曼家族从零解剖 链接 :卡尔曼家族从零解剖-(00)目录最新无死角讲解:https://blog.csdn.net/weixin_43013761/article/details/133846882 文末正下方中心提供了本人 联系…...

macOS使用conda初体会
最近在扫盲测序的一些知识 其中需要安装一些软件进行练习,如质控的fastqc,然后需要用conda来配置环境变量和安装软件。记录一下方便后续查阅学习 1.安装miniconda 由于我的电脑之前已经安装了brew,所以我就直接用brew安装了 brew install …...

GetPrivateProfileSection使用
基本语法 GetPrivateProfileSection 是一个 Windows API 函数,用于检索指定 INI 文件中特定节的所有键值对。它可以读取INI文件中指定节所有的键值对并将结果存储在指定的缓冲区中。 以下是 GetPrivateProfileSection 函数的基本语法: DWORD GetPriva…...

Ubuntu20.04 安装 Matlab R2021a
1. 压缩包分卷解压缩 将下载下来的压缩包分卷解压缩 Ubuntu自带的archive会解压出错,不适用于分卷解压。 需要下载7zip (sudo apt-get install 走起) zip -F xxx.zip --out XXX.zip # xxx为主文件名 # XXX.zip为输出路径,上面的…...

让35岁程序员精力充沛的方法
最近重新阅读了《掌控:开启不疲惫、不焦虑的人生》这本书。这本书曾经对我减重20斤产生了巨大的影响。自然入睡、自然醒来,能够高效地工作和享受生活,这才是我们渴望的掌控感。以下是一些笔记: 少吃比多运动更有效地控制体重 每…...
01:2440----点灯大师
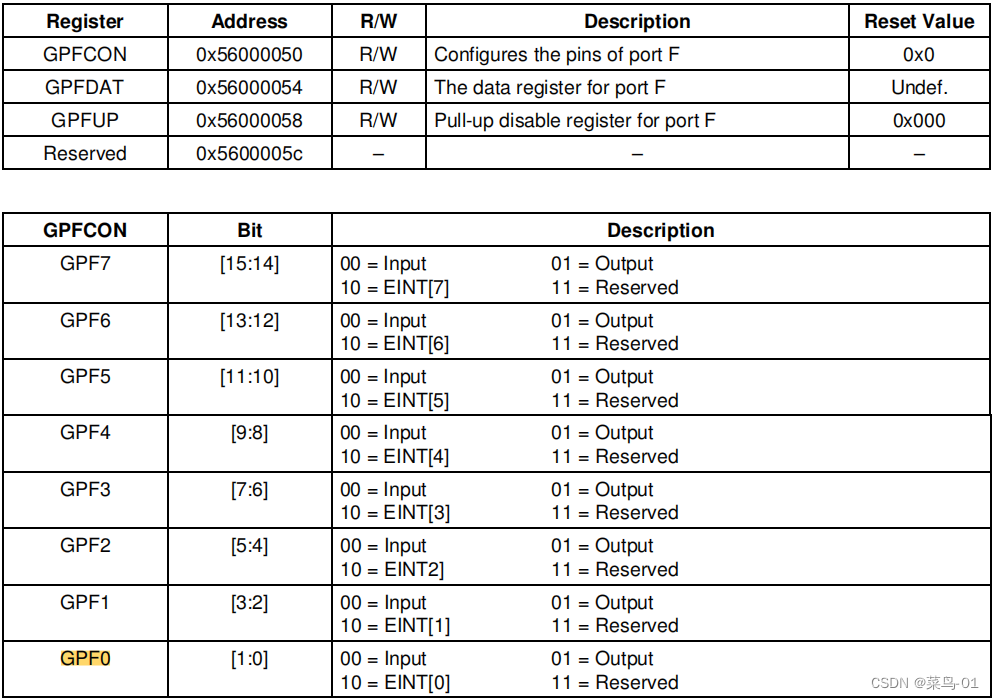
目录 一:点亮一个LED 1:原理图 2:寄存器 3:2440的框架和启动过程 A:框架 B:启动过程 4:代码 5:ARM知识补充 6:c语言和汇编的应用 A:代码 B:分析汇编语言 C:内存空间 7:内部机制 二:点亮2个灯 三:流水灯 四:按键控制LED 1:原理图 2:寄存器配置 3:代码 一:点…...
初步了解 RabbitMQ
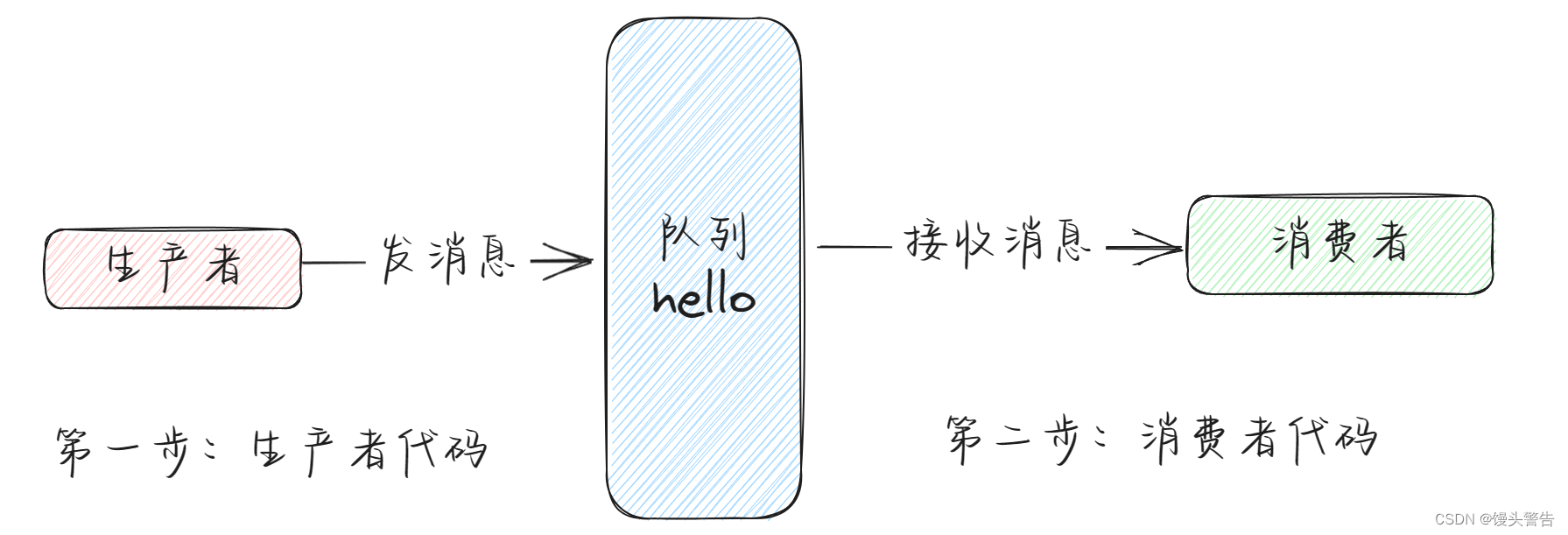
目录 编辑一、MQ 概述 1、MQ 的简介 2、MQ 的用途 (1)限流削峰 (2)异步解耦 (3)数据收集 二、RabbitMQ 概述 1、RabbitMQ 简介 2、四大核心概念 3、RabbitMQ 的核心部分 编辑 4、名词解释: 三、Hello …...

Faster-RCNN and Mask-RCNN框架解析
由于本人记忆力实在太差,每次学完一个框架没过多久就会忘,而且码文能力不行,人又懒,所以看到了其他人写的不错的两篇框架解析的博文,先来记录一下,就当是我写的喽 Faster-rcnn详解_faster r-cnn-CSDN博客 M…...
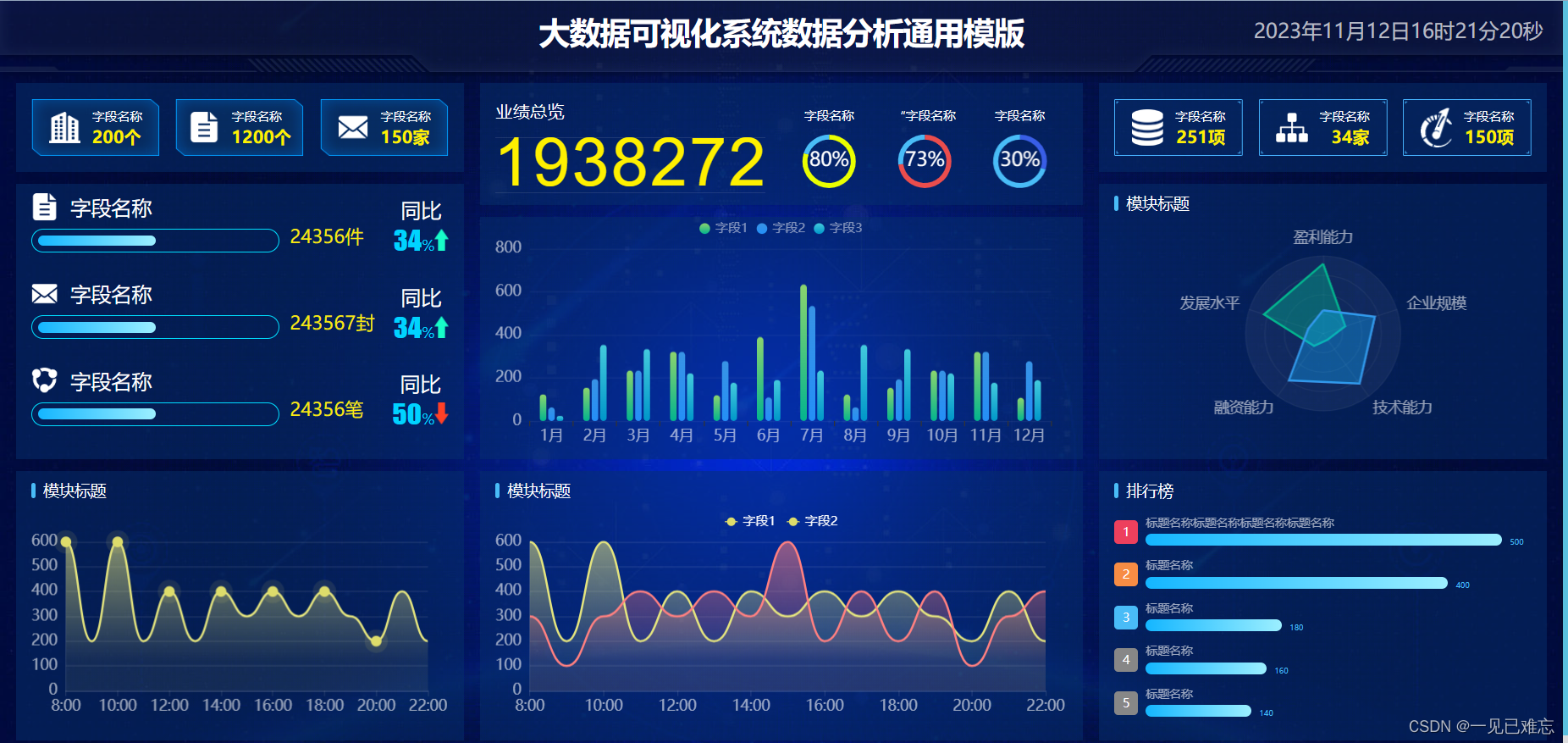
大数据可视化数据大屏可视化模板【可视化项目案例-05】
🎉🎊🎉 你的技术旅程将在这里启航! 🚀🚀 本文选自专栏:可视化技术专栏100例 可视化技术专栏100例,包括但不限于大屏可视化、图表可视化等等。订阅专栏用户在文章底部可下载对应案例源码以供大家深入的学习研究。 🎓 每一个案例都会提供完整代码和详细的讲解,不…...

Vue Router active-class 属性
active-class 是 vue-router 模块的 router-link 组件的属性,当 router-link 标签被点击时将会应用这个样式。 单独在 router-link 标签上使用 active-class 属性 <router-link to"/about" active-class"active">about</router-link…...
Error creating bean with name ‘apiModelSpecificationReader‘ defined in URL
问题: 启动项目的时候,报错了 org.springframework.beans.factory.UnsatisfiedDependencyException: Error creating bean with name apiModelSpecificationReader defined in URL [jar:file:/D:/.gradle/caches/modules-2/files-2.1/io.springfox/sp…...

CS224W6.2——深度学习基础
在本文中,我们回顾了深度学习的概念和技术,这些概念和技术对理解图神经网络至关重要。从将机器学习表述为优化问题开始,介绍了目标函数、梯度下降、非线性和反向传播的概念。 文章目录 1. 大纲2. 优化问题2.1 举例损失函数 3. 如何优化目标函…...

Linux c/c++服务器开发实践
在Linux C开发环境中,通常有两种方式来开发多线程程序,一种是利用POSIX多线程 API函数来开发多线程程序,另外一种是利用C自带线程类来开发程序。 常见的与线程相关的基本API函数: API函数含义pthread_create创建线程pthread_exi…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
