如何判断一个角是否大于180度（2）

理论计算见上一篇：

如何判断一个角是否大于180度？_kv1830的博客-CSDN博客

此篇为代码实现

一。直接上代码：

import cv2 as cv
import numpy as np
import mathdef get_vector(p_from, p_to):return p_to[0] - p_from[0], p_to[1] - p_from[1]def get_unit_vector(v):"""获取单位向量"""x, y = vlength = (x ** 2 + y ** 2) ** 0.5return x / length, y / lengthdef calc_angle_by_sincos(sin, cos):if sin >= 0 and cos >= 0:angle = math.asin(sin)elif cos < 0:angle = math.pi - math.asin(sin)elif sin < 0 and cos >= 0:angle = math.asin(sin) + math.pi * 2else:raise ValueError(f'ignore case: sin: {sin}, cos: {cos}')angle = angle * 180 / math.pireturn angledef calc_angle_by_axis_x(v):"""由向量计算与x轴的夹角，x轴顺时针到向量"""x, y = get_unit_vector(v)return calc_angle_by_sincos(y, x)def calc_angle(p_a, p_b, p_c):"""角点为p_b，由b_a顺时针转到b_c的角注：y轴向下，就是顺时针，比如在opencv中。y轴向上，就是逆时针。所以顺逆只在一念之间~~"""print(f'p_a: {p_a}, p_b: {p_b}, p_c: {p_c}')v_ba = get_vector(p_b, p_a)v_bc = get_vector(p_b, p_c)v_ba, v_bc = get_unit_vector(v_ba), get_unit_vector(v_bc)x1, y1 = v_bax2, y2 = v_bc# 求解旋转方程a = np.array([[-y1, x1], [x1, y1]], dtype=np.float32)b = np.array([x2, y2], dtype=np.float32)result_flag, (sin, cos) = cv.solve(a, b)sin = sin[0]cos = cos[0]print(f'sin = {sin}, cos = {cos}')angle = calc_angle_by_sincos(sin, cos)return anglepoints = [(0, 0), (0, 0), (0, 0)]
current_p_index = 0
img = None# mouse callback function
def draw_angle(event, x, y, flags, param):global points, current_p_index, imgif event == cv.EVENT_LBUTTONDOWN:if current_p_index == 0:img = np.zeros((800, 800, 3), dtype=np.uint8)points[current_p_index] = (x, y)cv.circle(img, (x, y), 10, (0, 0, 255), -1, cv.LINE_AA)if current_p_index > 0:last_p = points[current_p_index - 1]cv.line(img, (x, y), last_p, (255, 0, 0), 2, cv.LINE_AA)current_p_index += 1if current_p_index == 3:angle = calc_angle(points[0], points[1], points[2])print(f'angle = {angle}')current_p_index = 0start_angle = calc_angle_by_axis_x(get_vector(points[1], points[0]))end_angle = calc_angle_by_axis_x(get_vector(points[1], points[2]))if end_angle < start_angle:end_angle += 360print(f'other_angle: {end_angle - start_angle}')# end_angle = start_angle + angleprint(f'start_angle = {start_angle}, end_angle = {end_angle}')cv.ellipse(img, points[1], (15, 15), 0, start_angle, end_angle, (0, 255, 0), -1, cv.LINE_AA)cv.imshow('img', img)if __name__ == '__main__':cv.namedWindow('img', cv.WINDOW_NORMAL)img = np.zeros((800, 800, 3), dtype=np.uint8)cv.imshow('img', img)cv.setMouseCallback('img', draw_angle)cv.waitKey()cv.destroyAllWindows()

二。稍加说明

1.demo使用方法

直接运行，在画布上依次按鼠标左键，点出点1，点2，点3，然后触发角度计算，绿色部分表示算的是哪个角。

注：按照上篇的说法，应该是点1绕点2逆时针旋转到点3。但是这里做了个变化，不是逆时针了，是顺时针了！为啥呢，因为在opencv中，y轴正方向是向下的，所以如果要逆时针旋转，那上篇的旋转公式得变一下才行。如果不想改变也很简单，就是定为由点1绕点2顺时针旋转到点3，即我们要求的大角。

图1

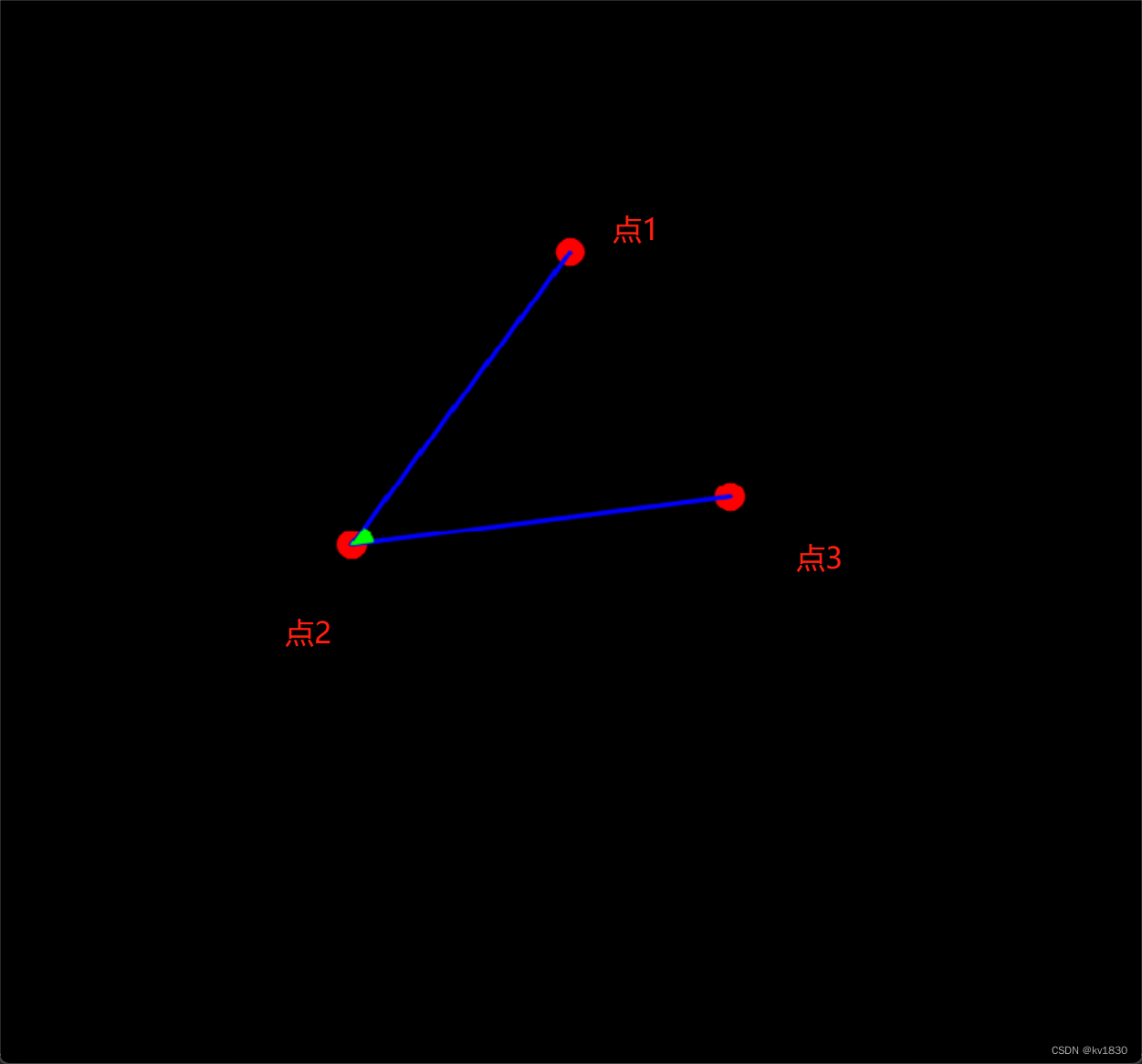
 运行结果如下图，红框里就是我们要求的值，绿框里的两个角度其实就图画的绿色的椭圆的起始角和终止角。 

 2.疑问

(1)这里会发现一个问题，其实不一定非得通过旋转公式来计算出旋转角，直接用终止边（图1的边2_3）的角度减去起始边（图1的边2_1）的角度，就可以得出旋转角的角度，但是这个角度有可能会小于0，此时直接把它加上360度，就OK了。其实这里可能为负的情况，就是起始边到终止边跨0度的问题，比如起始边是350度，终止边是10度，这样其实是顺时针转了20度，但是10-350会得到-340，再加360，就是20度啦。

3.更简单的方法

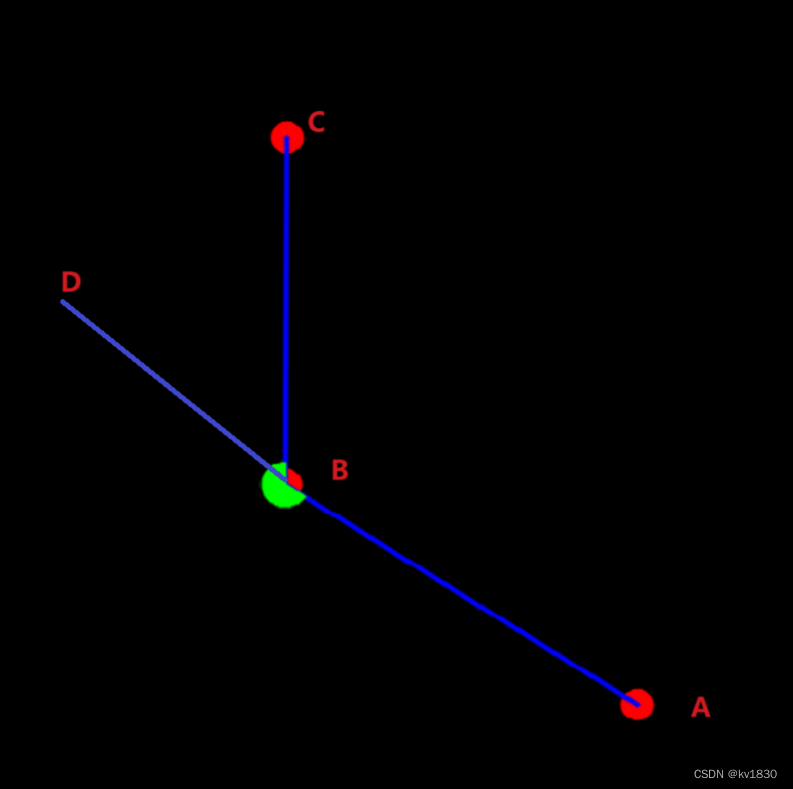
但是如果我们只想知道这个角是不是大于180度的话，其实还有一种结合旋转公式的更简单的判断方法，如下图，不再去求ABC的角，而是AB向量与BC向量的夹角（不过仍然是大角的概念），具体来说就是在AB延长线上取一点D，求的就是DBC大角，所以是D绕点B顺时针转到C的角度（注意这里顺时针是针对opencv y轴向下的情况）。

就下图来说求出来的DBC大角肯定是大于180度了，其sin值会小于0，相反，其对应的ABC就是小于180度。

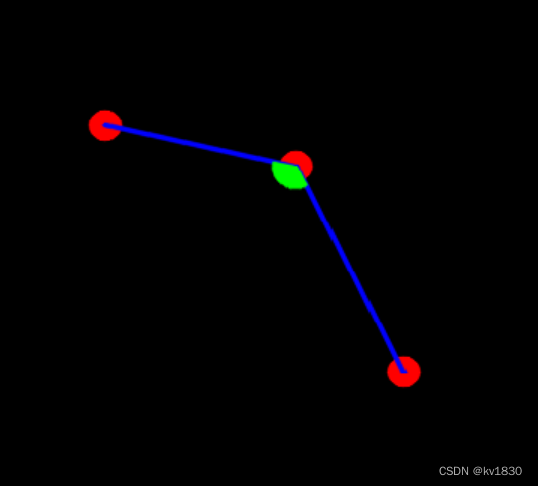
再来看一个大角ABC大于180度的情况，此时DBC是小于180度的，则其sin值大于0

所以综上，由旋转公式求DBC的sin值，小于0，则ABC是小于180度，否则大于180度（如果要看0度，那就是等于0喽）

直接放上修改后的代码。

import cv2 as cv
import numpy as np
import mathdef get_vector(p_from, p_to):return p_to[0] - p_from[0], p_to[1] - p_from[1]def get_unit_vector(v):"""获取单位向量"""x, y = vlength = (x ** 2 + y ** 2) ** 0.5return x / length, y / lengthdef calc_angle_by_sincos(sin, cos):if sin >= 0 and cos >= 0:angle = math.asin(sin)elif cos < 0:angle = math.pi - math.asin(sin)elif sin < 0 and cos >= 0:angle = math.asin(sin) + math.pi * 2else:raise ValueError(f'ignore case: sin: {sin}, cos: {cos}')angle = angle * 180 / math.pireturn angledef calc_angle_by_axis_x(v):"""由向量计算与x轴的夹角，x轴顺时针到向量"""x, y = get_unit_vector(v)return calc_angle_by_sincos(y, x)def judge_angle(p_a, p_b, p_c):"""角点为p_b，由b_a顺时针转到b_c的角注：y轴向下，就是顺时针，比如在opencv中。y轴向上，就是逆时针。所以顺逆只在一念之间~~"""print(f'p_a: {p_a}, p_b: {p_b}, p_c: {p_c}')v_ab = get_vector(p_a, p_b)v_bc = get_vector(p_b, p_c)v_ab, v_bc = get_unit_vector(v_ab), get_unit_vector(v_bc)x1, y1 = v_abx2, y2 = v_bc# 求解旋转方程a = np.array([[-y1, x1], [x1, y1]], dtype=np.float32)b = np.array([x2, y2], dtype=np.float32)result_flag, (sin, cos) = cv.solve(a, b)sin = sin[0]cos = cos[0]print(f'sin = {sin}, cos = {cos}')return sin < 0points = [(0, 0), (0, 0), (0, 0)]
current_p_index = 0
img = None# mouse callback function
def draw_angle(event, x, y, flags, param):global points, current_p_index, imgif event == cv.EVENT_LBUTTONDOWN:if current_p_index == 0:img = np.zeros((800, 800, 3), dtype=np.uint8)points[current_p_index] = (x, y)cv.circle(img, (x, y), 10, (0, 0, 255), -1, cv.LINE_AA)if current_p_index > 0:last_p = points[current_p_index - 1]cv.line(img, (x, y), last_p, (255, 0, 0), 2, cv.LINE_AA)current_p_index += 1if current_p_index == 3:result = judge_angle(points[0], points[1], points[2])print('小于180' if result else '大于180')current_p_index = 0start_angle = calc_angle_by_axis_x(get_vector(points[1], points[0]))end_angle = calc_angle_by_axis_x(get_vector(points[1], points[2]))if end_angle < start_angle:end_angle += 360print(f'other_angle: {end_angle - start_angle}')# end_angle = start_angle + angleprint(f'start_angle = {start_angle}, end_angle = {end_angle}')cv.ellipse(img, points[1], (15, 15), 0, start_angle, end_angle, (0, 255, 0), -1, cv.LINE_AA)cv.imshow('img', img)if __name__ == '__main__':cv.namedWindow('img', cv.WINDOW_NORMAL)img = np.zeros((800, 800, 3), dtype=np.uint8)cv.imshow('img', img)cv.setMouseCallback('img', draw_angle)cv.waitKey()cv.destroyAllWindows()

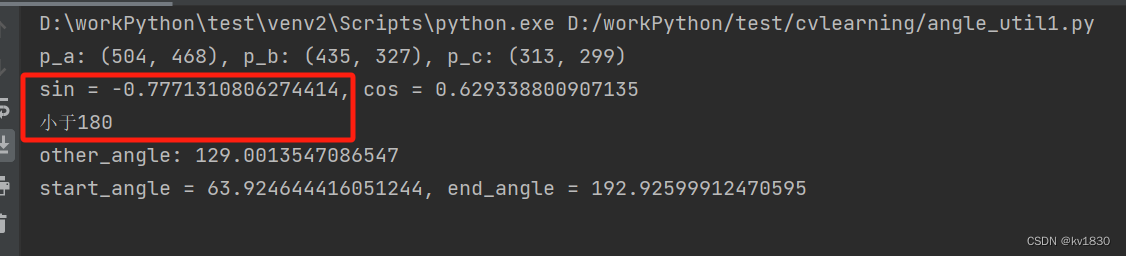
这里为什么说更简单呢，因为不用再根据正弦余弦的4种情况来求角，也没用到反正弦反余弦，只要判断一下sin值的正负就行了，是不是更简单一点。