100127. 给小朋友们分糖果 II
给你两个正整数 n 和 limit 。
请你将 n 颗糖果分给 3 位小朋友,确保没有任何小朋友得到超过 limit 颗糖果,请你返回满足此条件下的 总方案数 。
示例 1:
输入:n = 5, limit = 2 输出:3 解释:总共有 3 种方法分配 5 颗糖果,且每位小朋友的糖果数不超过 2 :(1, 2, 2) ,(2, 1, 2) 和 (2, 2, 1) 。
示例 2:
输入:n = 3, limit = 3 输出:10 解释:总共有 10 种方法分配 3 颗糖果,且每位小朋友的糖果数不超过 3 :(0, 0, 3) ,(0, 1, 2) ,(0, 2, 1) ,(0, 3, 0) ,(1, 0, 2) ,(1, 1, 1) ,(1, 2, 0) ,(2, 0, 1) ,(2, 1, 0) 和 (3, 0, 0) 。
解析:
正难则反:我们先算出总方案数,在减去不合法的数即可。
有组合数学可以用隔板法进行求出总方案数。C(n+2,2)
在考虑不合法的数。
由容斥原理得:
考虑到三种情况:(这里要注意至少这个词语的理解)
1.当至少一个人不合法,那个人至少要limit+1个球,在用隔板法,在n-limit-1中经行分配 3*C(n- limit-1+2,2),由题意知道由三个人。
2.当至少有两个人不合法时,至少要消耗(limit+1)*2个球,分配的方案数为3⋅C(n−2⋅(limit+1)+2,2)
3.至少有三个人不合法时,分配的方案数为C(n−3⋅(limit+1)+2,2)
最后总方案数 - 不合法方案数即可。
在上面三种情况中有一些是重复被减去 所以后面要加上。
class Solution {
public:long long c2(long long n){return n > 1 ?n*(n-1)/2:0;}long long distributeCandies(int n, int limit) {return c2(n+2) - 3*c2(n-limit+1) + 3*c2(n-2 *limit) - c2(n-3*limit - 1);}
};相关文章:

100127. 给小朋友们分糖果 II
给你两个正整数 n 和 limit 。 请你将 n 颗糖果分给 3 位小朋友,确保没有任何小朋友得到超过 limit 颗糖果,请你返回满足此条件下的 总方案数 。 示例 1: 输入:n 5, limit 2 输出:3 解释:总共有 3 种方…...
【2】Spring Boot 3 项目搭建
目录 【2】Spring Boot 3 初始项目搭建项目生成1. 使用IDEA商业版创建2. 使用官方start脚手架创建 配置与启动Git版本控制 个人主页: 【⭐️个人主页】 需要您的【💖 点赞关注】支持 💯 【2】Spring Boot 3 初始项目搭建 项目生成 1. 使用IDEA商业版创…...

【第七章】软件设计师 之 程序设计语言与语言程序处理程序基础
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 1、前言 正规式 2、编译过程 编译型&…...
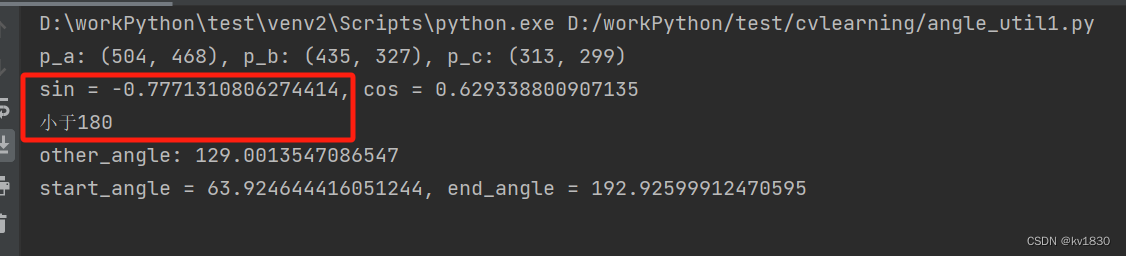
如何判断一个角是否大于180度(2)
理论计算见上一篇: 如何判断一个角是否大于180度?_kv1830的博客-CSDN博客 此篇为代码实现 一。直接上代码: import cv2 as cv import numpy as np import mathdef get_vector(p_from, p_to):return p_to[0] - p_from[0], p_to[1] - p_from…...

ASAM OpenDRIVE V1.7协议超详解(一)
文章目录 前言一、仿真场景的构成二、openDRIVE框架三、g_additionalData四、openDRIVE-header五、openDRIVE-road1、Road总拓扑结构2、Road-link介绍1)link的拓扑结构2)link链接示例3)link前继后继4)道路link规则 3、road-type介…...
springboot的配置信息的设置和读取(application.properties/application.yml)
springboot提供了两种配置信息的文件格式,application.properties和application.yml,基于直接明了,使用方便和高效的前提下下面的配置均采用yml格式配置, 注意 yml采用缩减方式来排列键后面紧跟冒号,然后空格&#x…...
Deepsort项目详解
一、目标追踪整体代码 代码目录如下图所示: 、 追踪相关代码: 检测相关代码和权重 调用 检测 和 追踪的代码: 首先代码分为三个部分: 目标追踪的相关代码和权重目标检测相关代码和权重,这里用的是yolov5.5目标检…...
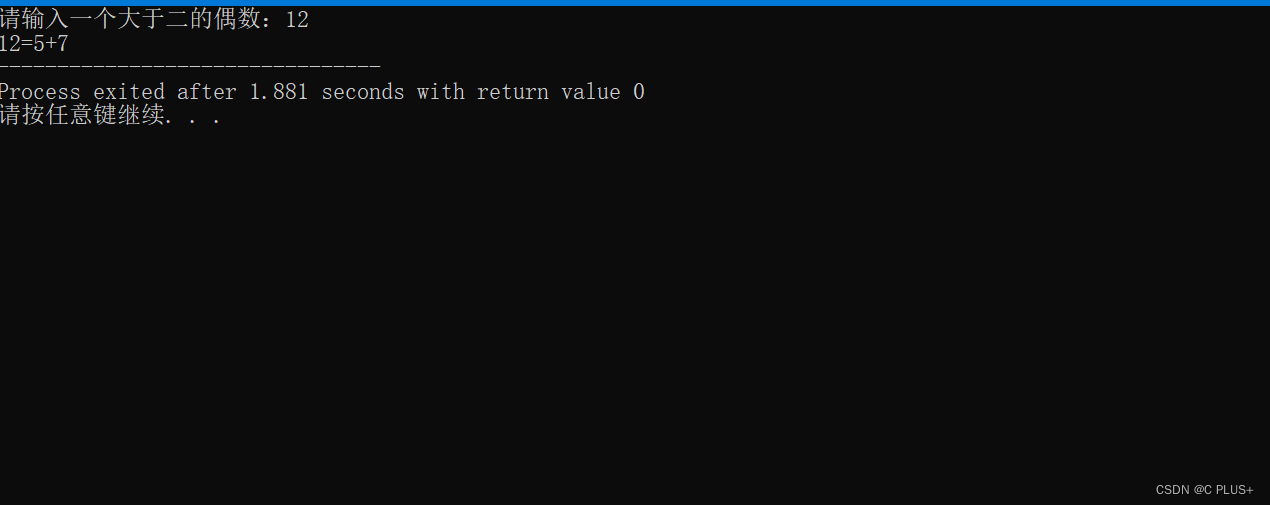
C语言证明一个偶数总能表示为两个素数之和。输入一个偶数并将其分解为两个素数
完整代码: // 一个偶数总能表示为两个素数之和。输入一个偶数并将其分解为两个素数#include<stdio.h>//判断一个数n是否为素数 int isPrimeNumber(int n){//1不是素数if (n1){return 0;}for (int i 2; i <(n/2); i){//当有n能被整除时,不是素…...

Python 的 datetime 模块
目录 简介 一、date类 (一)date 类属性 (二)date 类方法 (三)实例属性 (四)实例的方法 二、time类 (一)time 类属性 (二)tim…...
Termius for Mac:掌控您的云端世界,安全高效的SSH客户端
你是否曾经在Mac上苦苦寻找一个好用的SSH客户端,让你能够远程连接到Linux服务器,轻松管理你的云端世界?现在,我们向你介绍一款强大而高效的SSH客户端——Termius。 Termius是一款专为Mac用户设计的SSH客户端,它提供了…...

Ubuntu 下监控并自动重启网卡
很多时候网站服务器挂掉也可能是因为网卡挂掉了,如果你网站不能访问时 SSH 也无效了一般都是这个问题。这时可以通过一个定时脚本监控网络并进行自动重启。 1 创建脚本 auto_restart_network.sh 4 5 6 7 8 9 #!/bin/bash ping www.baidu.com -c 1 >/dev/null i…...

377. 组合总和 Ⅳ
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。 题目数据保证答案符合 32 位整数范围。 示例 1: 输入:nums [1,2,3], target 4 输出:7 解释&#…...

【OpenCV】计算视频的光流并跟踪物体calcOpticalFlowPyrLK
一、介绍 计算光流可以使用OpenCV的calcOpticalFlowPyrLK方法,cv2.calcOpticalFlowPyrLK是OpenCV库中的一个函数,用于计算稀疏光流。它实现的是Lucas-Kanade方法,这是一种常用的光流计算方法。 光流是图像中物体运动的近似表示&#…...

C语言进阶
数组 在基础篇说过,数组实际上是构造类型之一,是连续存放的。 一维数组 定义 定义格式:[存储类型] 数据类型 数组名标识符[下标]; 下面分模块来介绍一下数组的定义部分的内容。 1、初始化和元素引用: 可以看到数组是连续存储…...

Linux之gdb
gdb就是一个Linux的调试工具,类似与vs里面的调试 可执行程序也有格式,不是简单的二进制堆砌...
——第3天:风控建模中如何处理缺失值?)
100天精通风控建模(原理+Python实现)——第3天:风控建模中如何处理缺失值?
风控模型已在各大银行和公司都实际运用于业务,用于营销和风险控制等。 之前已经阐述了100天精通风控建模(原理+Python实现)——第1天:什么是风控建模? 100天精通风控建模(原理+Python实现)——第2天:风控建模有什么目的? 接下来看下100天精通风控建模(原理…...
Leetcode—680.验证回文串II【简单】
2023每日刷题(二十七) Leetcode—680.验证回文串II 实现代码 class Solution { public:bool judgeFunc(string s, int left, int right) {while(left < right) {if(s[left] ! s[right]) {return false;}left;right--;}return true;}bool validPalin…...

Redis五种数据类型及命令操作(二)
🎈个人公众号:🎈 :✨✨✨ 可为编程✨ 🍟🍟 🔑个人信条:🔑 知足知不足 有为有不为 为与不为皆为可为🌵 🍉本篇简介:🍉 本篇记录Redis五种数据类型及命令操作,如…...
:MDA模型驱动架构及元数据系统设计)
低代码信创开发核心技术(三):MDA模型驱动架构及元数据系统设计
前言 写最后一篇文章的时候,我本人其实犹豫了半年,在想是否发布出这篇文章,因为可能会动了很多人的利益。所以这篇文章既是整个低代码信创开发的高度总结,也是最为精华的一部分,它点明了低代码中最为核心的技术。虽然…...
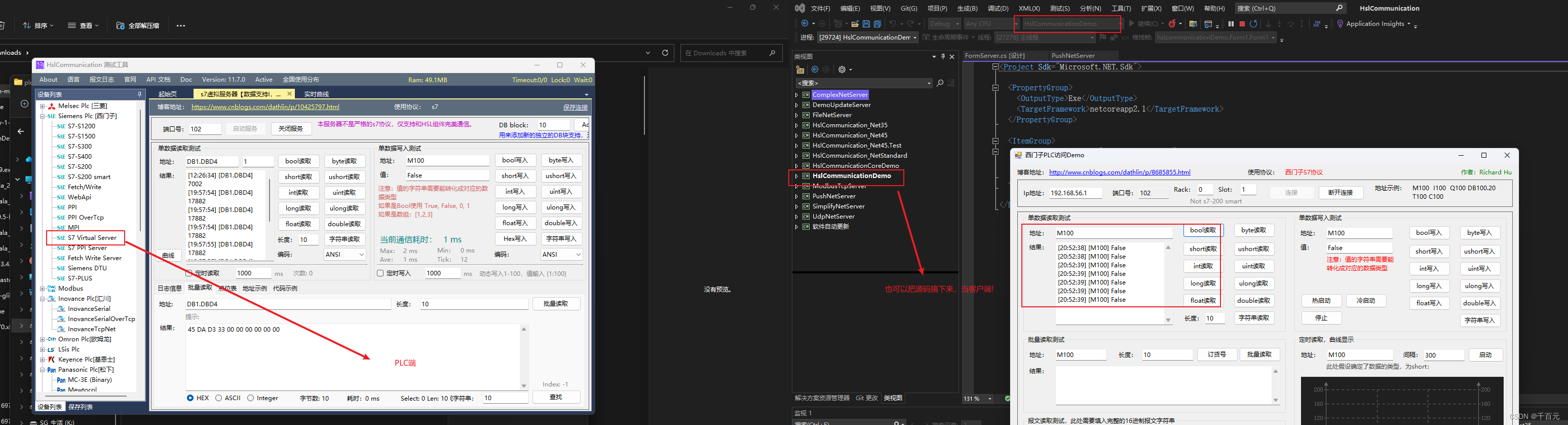
HslCommunication模拟西门子读写数据
导入HslCommunication C#端代码(上位机) 这里要注意的是上位机IP用的当前电脑的IP。 using HslCommunication; using HslCommunication.Profinet.Siemens; using System; using System.Collections.Generic; using System.ComponentModel; using Syste…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...
