【数据结构】二叉树经典例题---<你真的掌握二叉树了吗?>(第一弹)
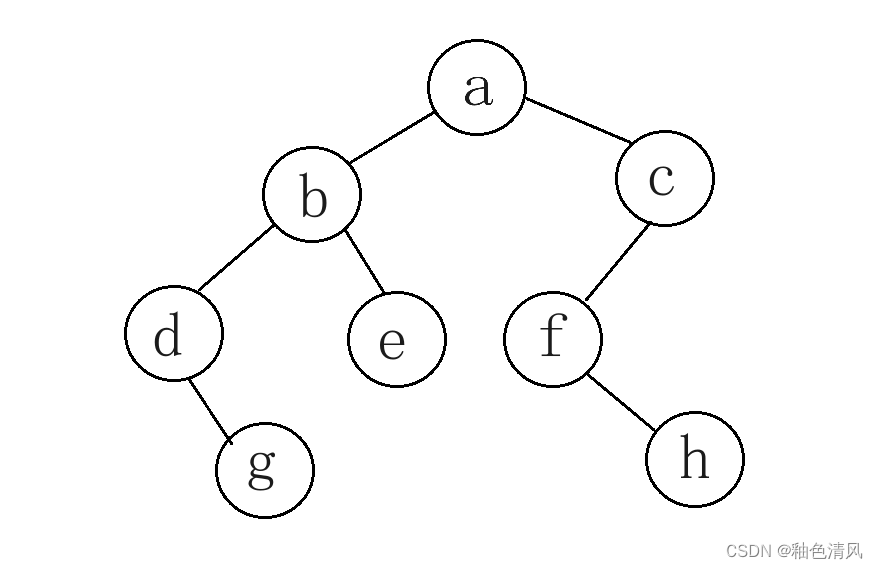
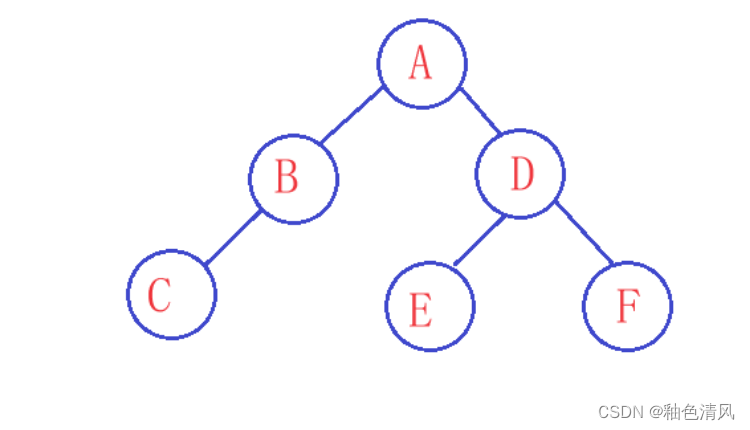
一、已知一颗二叉树如下图,试求:
(1)该二叉树前序、中序和后序遍历的结果。
(2)该二叉树是否为满二叉树?是否为完全二叉树?
(3)将它转换成对应的树或森林。
(4)这颗二叉树的深度为多少?
(5)试对该二叉树进行前序线索化。
(6)试对该二叉树极性中序线索化。
(1)
前序遍历(根左右): a->b->d->g->e->c->f->h
中序遍历(左根右): d->g->b->e->a->f->h->c
后序遍历(左右根): g->d->e->b->h->f->c->a
(2)
该二叉树不是满二叉树,也不是完全二叉树。
(3)
二叉树到树和森林的转换,步骤如下:
(1)首先将二叉树按照逆时针方向旋转45°。
(2)若某结点是其双亲的左子女,则把该结点的右子女、右子女的右子女…都与该结点的双亲用线连起来。
(3)最后去掉原二叉树中所有双亲到齐右子女的连线。
对于上面这棵树,我们首先将其旋转,将并用线连接:
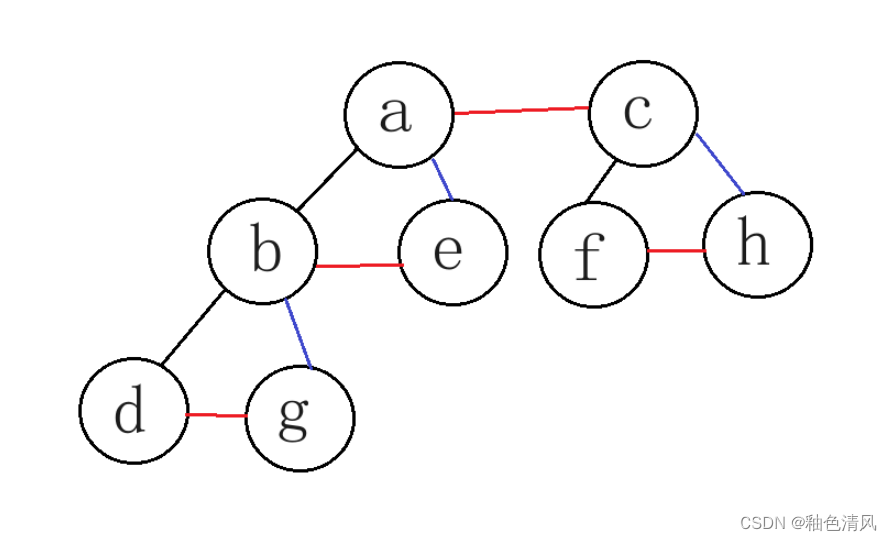
然后我们删除所有双亲到其右子女的连线,也就是红色的线:
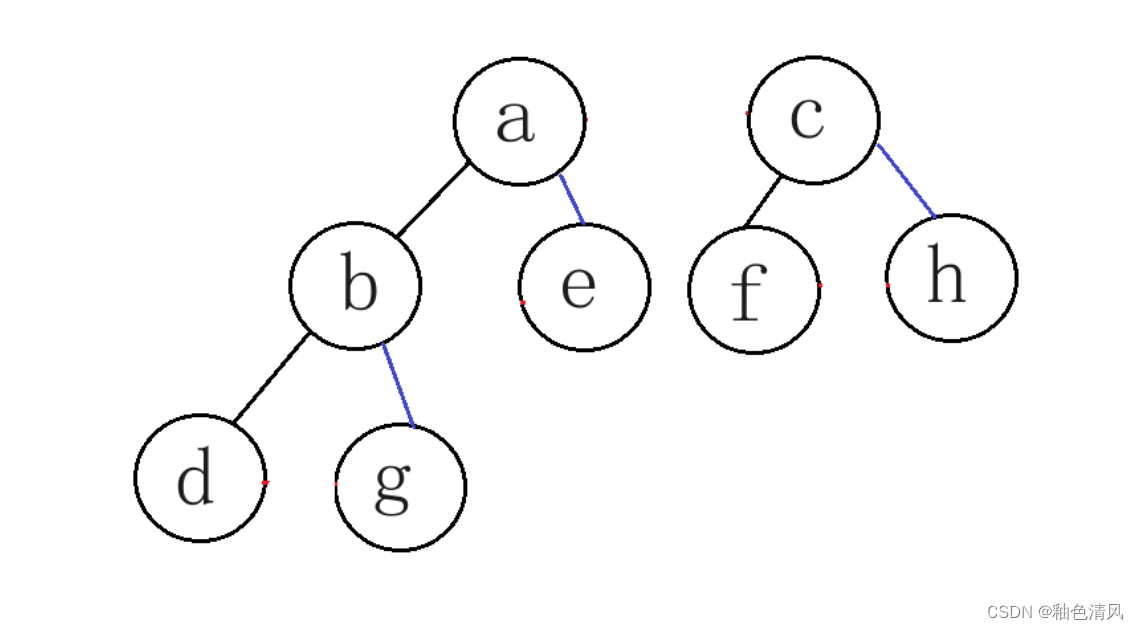
这样我们就把一颗二叉树转换成为森林了。
(4)这棵树的深度为4。
(5)对这颗二叉树进行前序线索化:
穿线二叉树
所谓穿线二叉树,即在一般二叉树的基础上,对每个结点进行考察。
若其左子树为非空,则其左指针不变,仍指向左子女;
若其左子树为空,则让其左指针指向某种遍历顺序下该结点的前驱结点;
若其右子树非空,则其右指针不变,仍指向右子女;
若其右子树为空,则让右子树指向某种遍历顺序下该节点的后继结点。
前序线索化: a->b->d->g->e->c->f->h
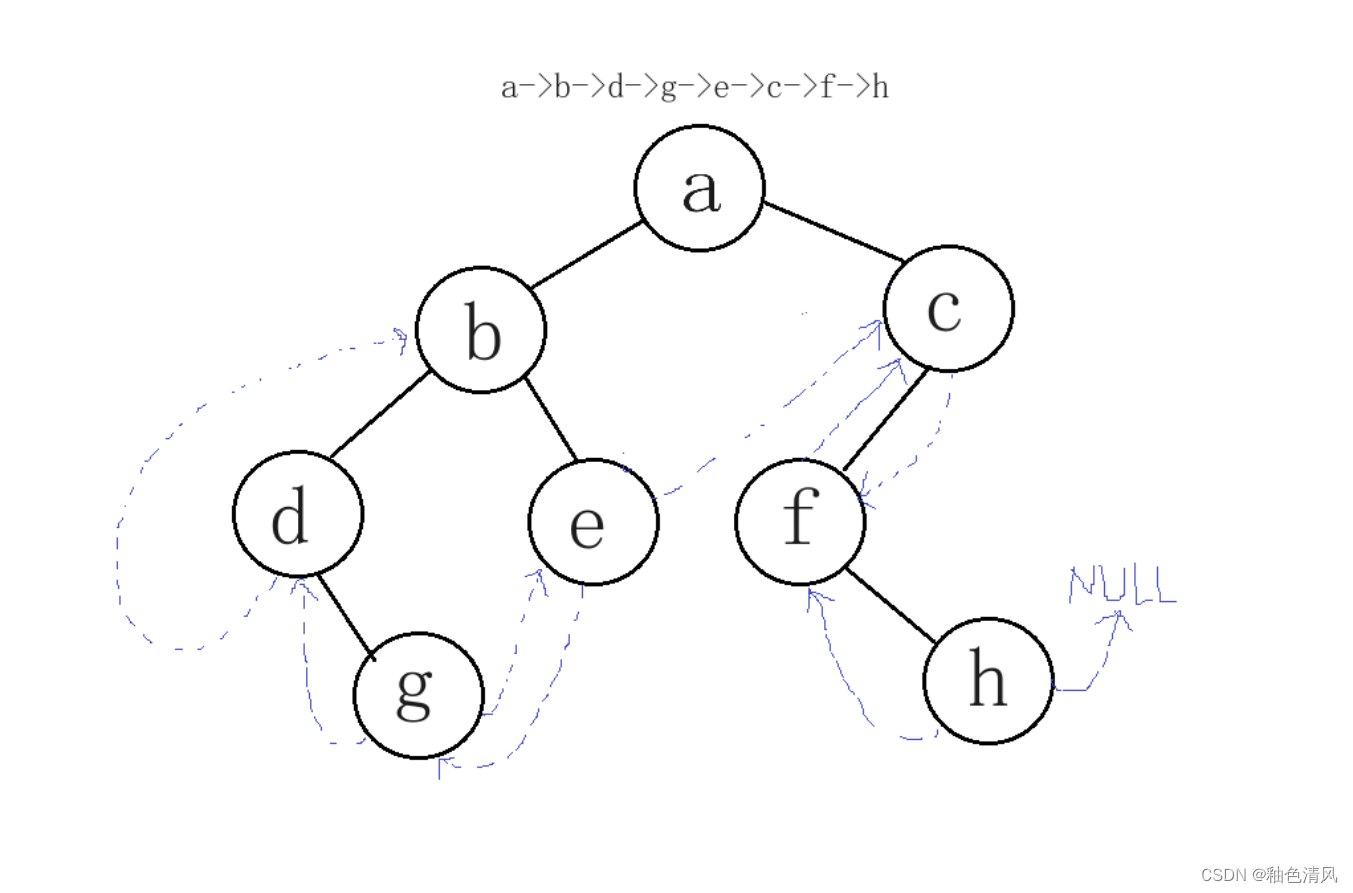
(6)中序线索化: d->g->b->e->a->f->h->c

二、试描述树和二叉树的主要区别
一、性质不同:树是一种数据结构,二叉树是每个结点最多有两个子树的一种树结构。
二、结点不同:树的每个结点有零个或多个子结点,二叉树每个结点最多有两个子树。
三、种类不同:树的种类包括无序树、有序树、二叉树和霍夫曼树等,二叉树的种类包括完全二叉树、满二叉树和平衡二叉树。
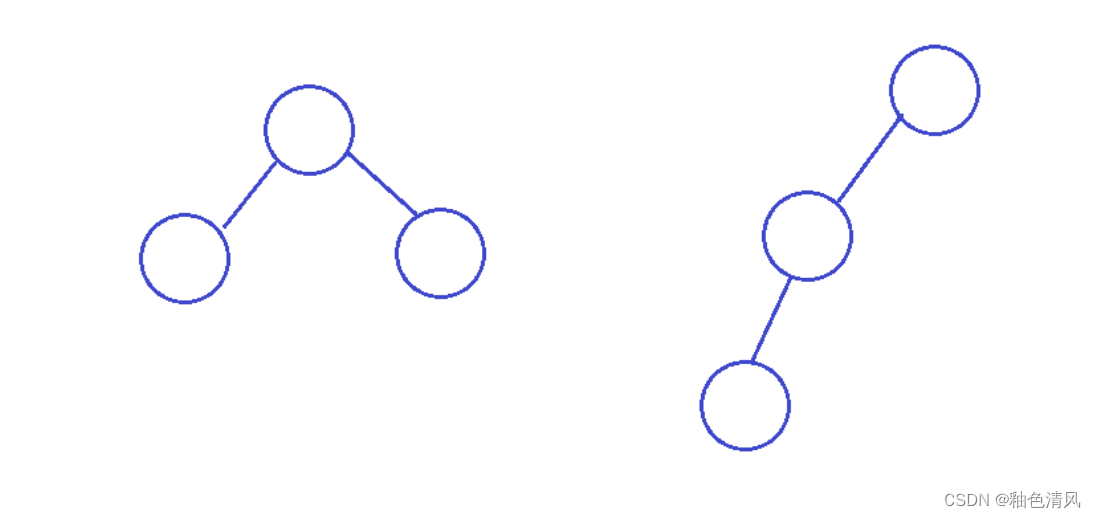
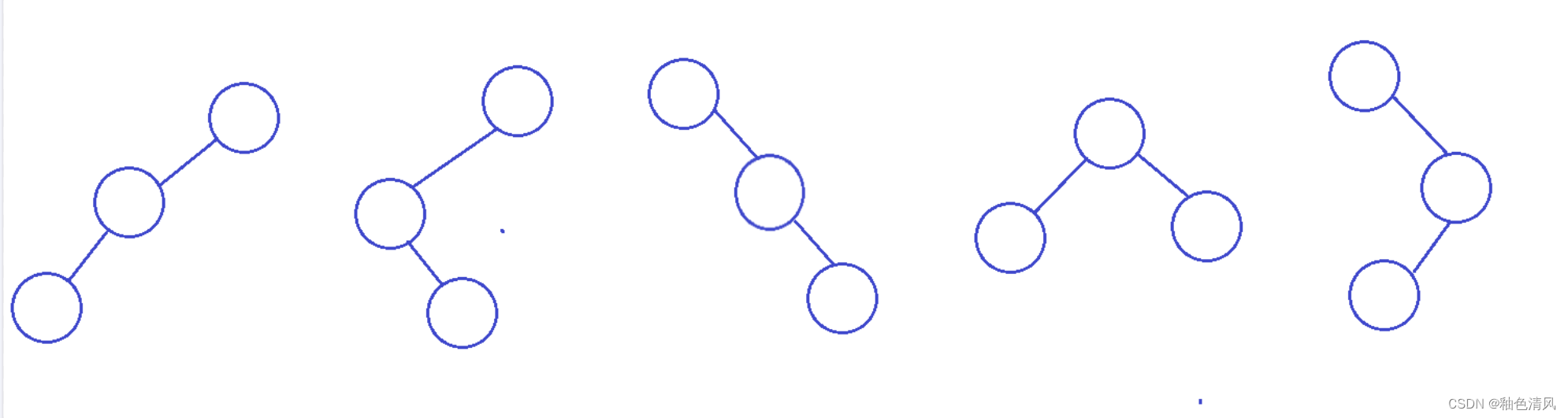
三、试分别画出来具有3个结点的树和具有3个结点的二叉树的所有不同形态。
这里主要考察树和二叉树的区别,树是无序的,而二叉树是有序的。
树:
二叉树:
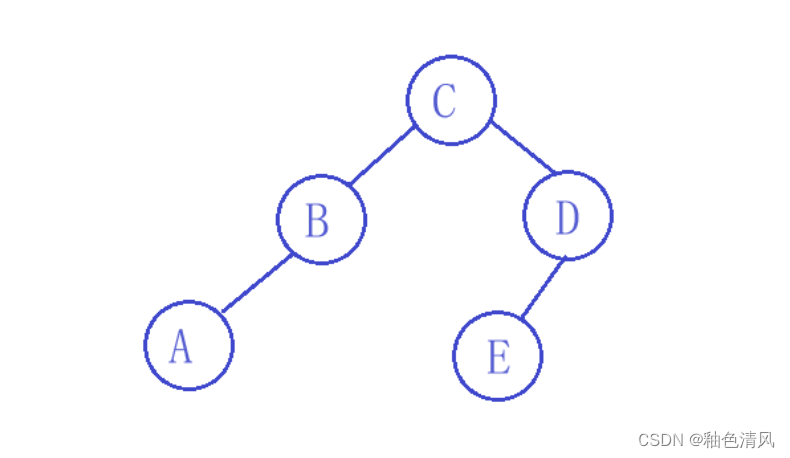
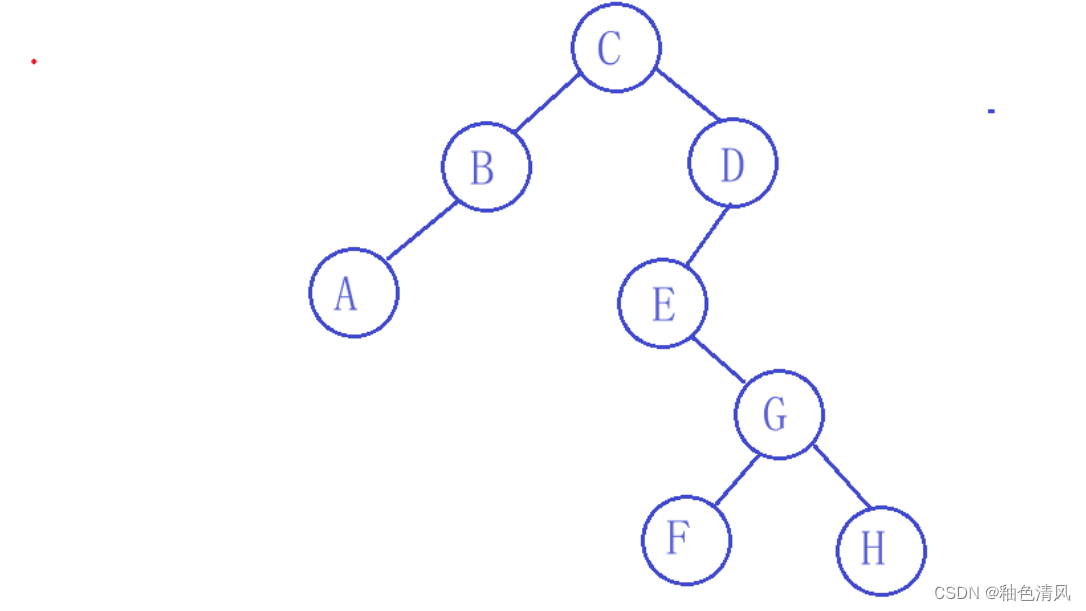
四、已知一颗二叉树的中序遍历结果为ABCEFGHD,后序遍历结果为ABFHGEDC,试画出此二叉树。
中序遍历,即 左子树->根->右子树
后序遍历,即 左子树->右子树->根
故由此,我们首先可以根据后序遍历得知这棵树的根节点为C。

我们可以得知,左子树的结点为AB,右子树包含结点为 EFGHD。
对于左子树,中序(左根右)和后序(左右根)一样,那么可以推断A为左子树结点的左孩子,B为根。
对于右子树后序遍历结果< FHGED >我们可以得知右子树的根节点为D。确定之后,再根据前序遍历< EFGHD>可以得知< EFGH >全部为 左子树上的结点。
根据基本判断先得出:
中序< EFGH>和后序< FHGE >可以得知,< FGH>为E的右子树,然后根据后序 可以得之,G为结点。
G为子树的结点,根据中序可以得知,F为左结点,H为右结点。
五、已知一颗二叉树的前序遍历结果为ABCDEF,中序遍历的结果为CBAEDF,试画出此二叉树。
前序:根左右ABCDEF
中序:左根右CBAEDF
这个题给出前序和中序,中序其实就是将所有的结点压下去,压在同一水平线上,然后进行排序。
(前序遍历其实就是顺着结点沿着左线而下。)
根据前序,确定这棵树的根节点为A。
然后确定左子树,和右子树

相关文章:

【数据结构】二叉树经典例题---<你真的掌握二叉树了吗?>(第一弹)
一、已知一颗二叉树如下图,试求: (1)该二叉树前序、中序和后序遍历的结果。 (2)该二叉树是否为满二叉树?是否为完全二叉树? (3)将它转换成对应的树或森林。 (4)这颗二叉树的深度为多少? (5)试对该二叉树进行前序线索化。 (6)试对…...
基于springboot实现桥牌计分管理系统项目【项目源码】
基于springboot实现桥牌计分管理系统演示 JAVA简介 JavaScript是一种网络脚本语言,广泛运用于web应用开发,可以用来添加网页的格式动态效果,该语言不用进行预编译就直接运行,可以直接嵌入HTML语言中,写成js语言&#…...
机器学习——朴素贝叶斯
目录 一、贝叶斯方法 背景知识 贝叶斯公式 二、朴素贝叶斯原理 判别模型和生成模型 1.朴素贝叶斯法是典型的生成学习方法 2.朴素贝叶斯法的基本假设是条件独立性 3.朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测 用于文…...

【PTE-day07 文件上传2】
1、常见的绕过方式 (1)畸形后缀名绕过 .php、.pht、.php3、.php4、.php5、.php2、.phtml、.pHp、.html、.Htm......(2)双写过滤字符绕过 (3).htaccess文件绕过 <FilesMatch "jpg"> SetHandler application/x-httpd-php...
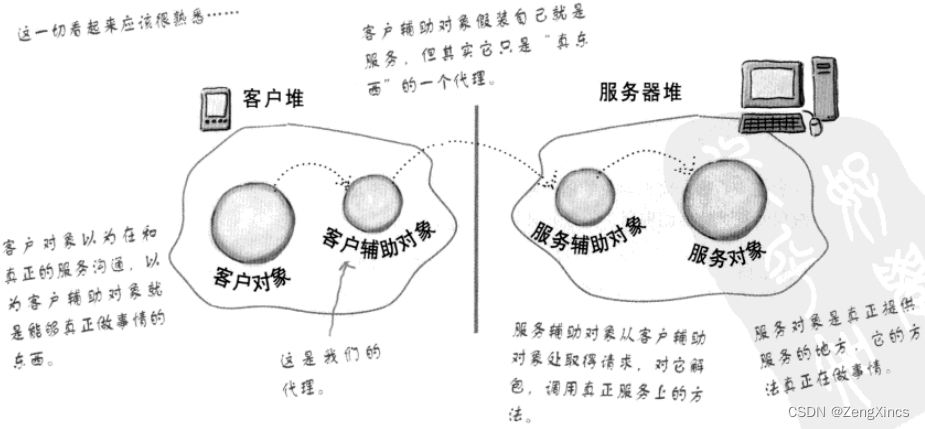
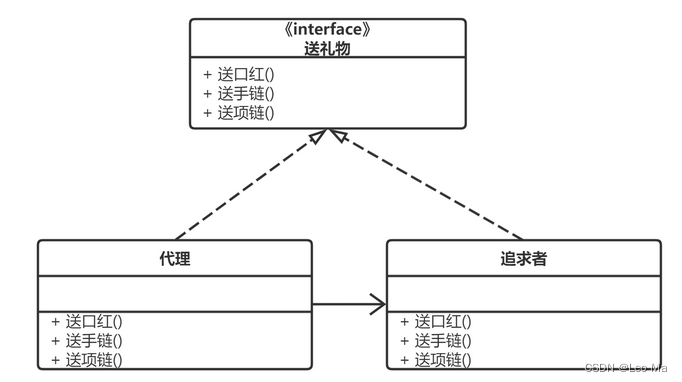
设计模式之十一:代理模式
代理可以控制和管理访问。 RMI提供了客户辅助对象和服务辅助对象,为客户辅助对象创建和服务对象相同的方法。RMI的好处在于你不必亲自写任何网络或I/O代码。客户程序调用远程方法就和运行在客户自己本地JVM对对象进行正常方法调用一样。 步骤一:制作远程…...

在spring boot中调用第三方接口时重试问题
文章目录 前言 spring-retry对第三方接口做重试,和处理操作 一、引入依赖 <!--重试请求的注解依赖--><dependency><groupId>org.springframework.retry</groupId><artifactId>spring-retry</artifactId></dependency>&l…...

记录一次多数据源配置失效的情况
说明:在一些复杂的业务情景,比如我们需要在一个订单审核通过后,在将数据库状态修改的同时,将订单与订单详细这两条数据写入到另一个数据库中。我们就可以通过在配置文件中,配置多数据源,然后通过在Mapper的…...

EasyExcel导出替换列中的变量
基于easyexcel2.0版本 easyexcel官网:https://easyexcel.opensource.alibaba.com/docs/2.x/quickstart/write 测试代码地址:https://gitee.com/wangtianwen1996/cento-practice/blob/master/src/test/java/com/xiaobai/easyexcel/DynamicHeadTest.java …...

机器人规划算法——将多边形障碍物离散到地图像素点上?
问题一:如何判断一个点是否在多边形区域内? 方法1:向量叉乘判别法 设多边形的顶点依次为A1,A2…An,要判断的点为P,那么分别计算向量PA1叉乘向量PA2,向量PA2叉乘向量PA3,…ÿ…...
windows11使用docker部署安装minio
时间 2023-11-08 windows11使用docker部署安装minio 目录 1.docker 下载镜像2.docker安装镜像3.访问控制台4.安装问题解决5.使用教程 1.docker 下载镜像 调整镜像源到国内,否则会很慢 docker pull minio/minio2.docker安装镜像 设置用户名和密码时需要注意&…...

【JavaEESpring】Spring Web MVC⼊⻔
Spring Web MVC 1. 什么是 Spring Web MVC1.1 什么是 MVC ?1.2 是什么 Spring MVC? 2. 学习 Spring MVC2.1 建立连接2.2 请求2.3 响应 3. 相关代码链接 1. 什么是 Spring Web MVC 官⽅对于 Spring MVC 的描述是这样的: 1.1 什么是 MVC ? MVC 是 Model View C…...
flutter逆向 ACTF native app
前言 算了一下好长时间没打过CTF了,前两天看到ACTF逆向有道flutter逆向题就过来玩玩啦,花了一个下午做完了.说来也巧,我给DASCTF十月赛出的逆向题其中一道也是flutter,不过那题我难度降的相当之低啦,不知道有多少人做出来了呢~ 还原函数名 flutter逆向的一大难点就是不知道l…...
【Redis】set 集合
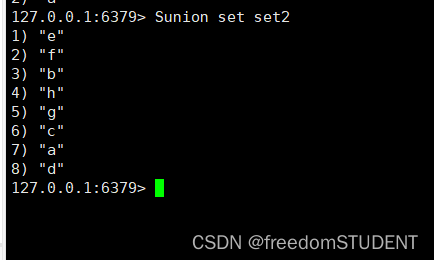
上一篇:list 列表 https://blog.csdn.net/m0_67930426/article/details/134364315?spm1001.2014.3001.5501 目录 Sadd Smembers Sismember Scard Srem 编辑Srandomember Spop Smove 集合类 Sdiff Sinter Sunion 官网 https://redis.io/commands/?…...
【算法与设计模式】
一、数据结构与算法 1、算法性能评估 时间复杂度、空间复杂度 2、数据结构 数组与列表 队列 堆栈 链表 二叉树 多叉树 递归算法 二、设计模式 1、单例 (1)GIL:线程互斥锁。保证同一时刻只有一个线程在进行。 (2)…...

Javaweb之javascript的小案例的详细解析
1.5.4 案例 1.5.4.1 需求说明 鲁迅说的好,光说不练假把式,光练不说傻把式。所以接下来我们需要通过案例来加强对于上述DOM知识的掌握。需求如下3个: 点亮灯泡 将所有的div标签的标签体内容后面加上:very good 使所有的复选框呈现被选中的…...
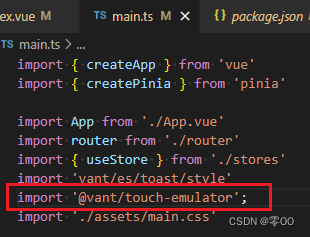
Vant 移动端UI 组件自动引入
Vue项目中安装Vant # Vue 3 项目,安装最新版 Vant npm i vant 组件按需引入配置 Vant按需引入- - -安装:unplugin-vue-components 插件 unplugin-vue-components 插件可以在Vue文件中自动引入组件(包括项目自身的组件和各种组件库中的组件&…...
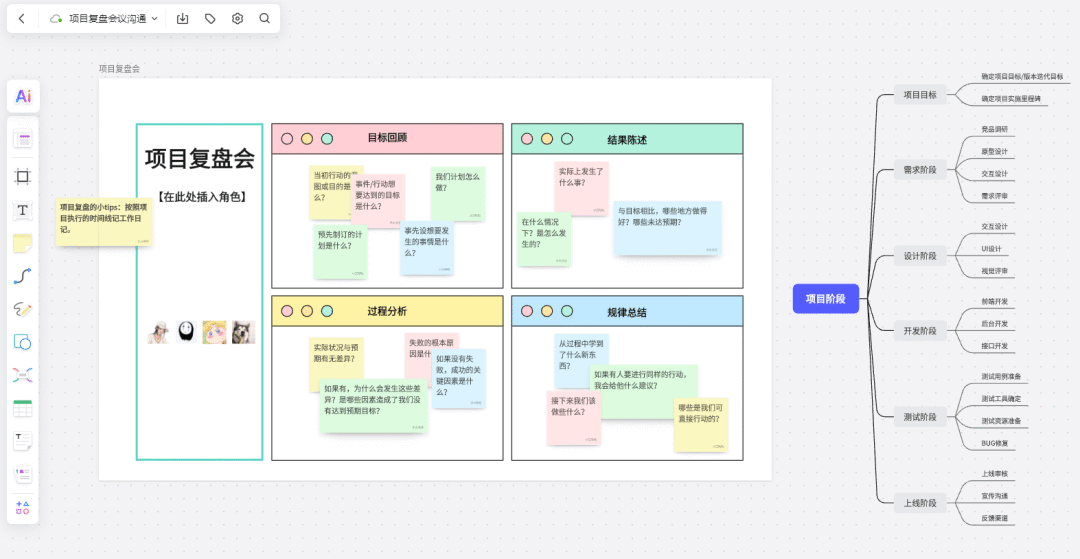
敏捷开发是什么?敏捷开发流程是怎么样的?
1. 什么是敏捷开发? 敏捷开发是一种迭代、增量式的软件开发方法,旨在通过灵活、协作和快速响应变化的方式,提高开发团队的效率和产品的质量。相较于传统的瀑布式开发模型,敏捷开发更加注重用户需求的响应和团队协作࿰…...
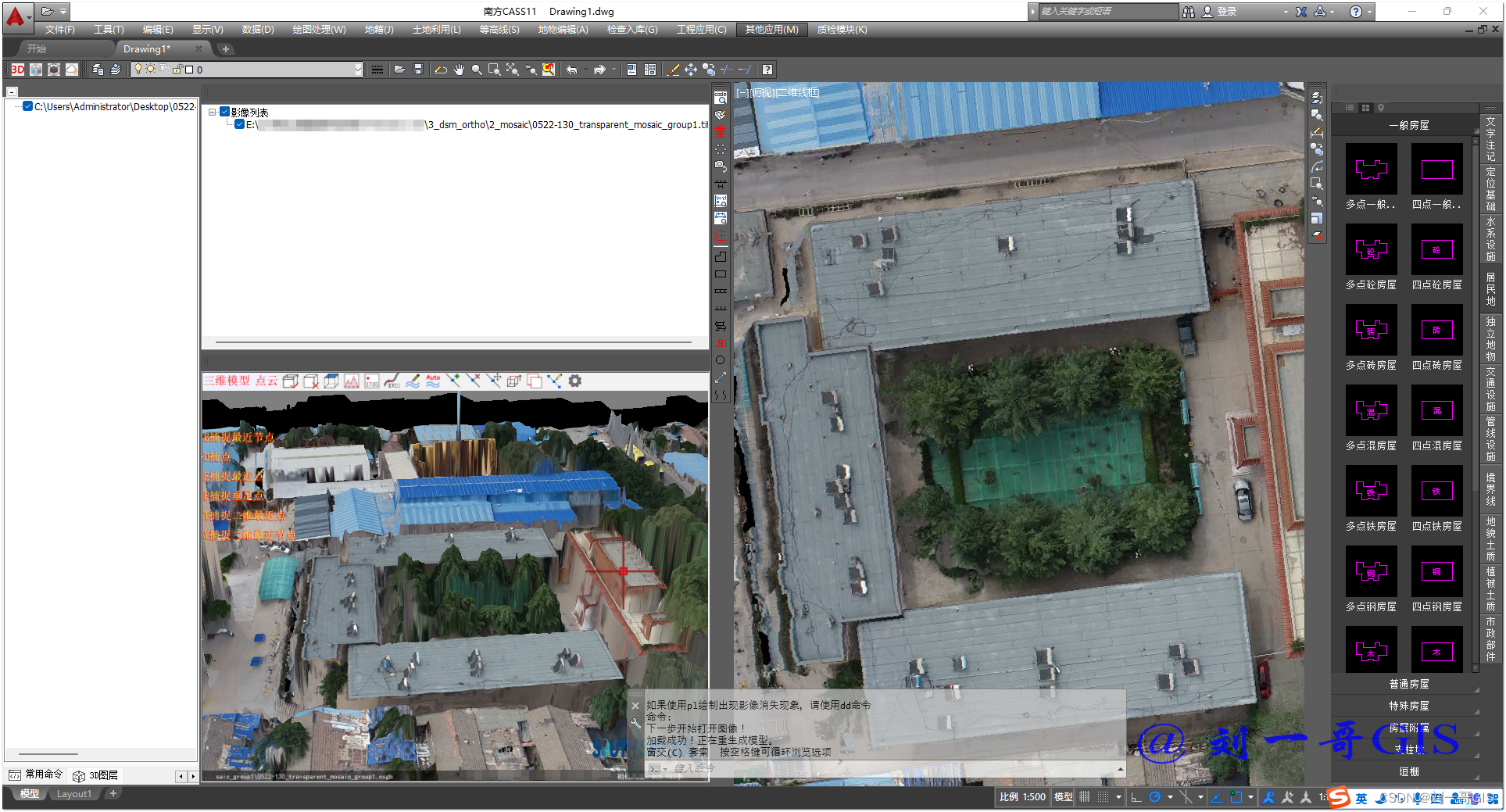
【CASS精品教程】cass3d 11.0加载超大影像、三维模型、点云数据
CAD2016+CASS11.0(内置3d)下载与安装: 【CASS精品教程】CAD2016+CASS11.0安装教程(附CASS11.0安装包下载)https://geostorm.blog.csdn.net/article/details/132392530 一、cass11.0 3d支持的数据 cass11.0中的3d模块增加了多种数据的支持,主要有: 1. 三维模型 点击…...
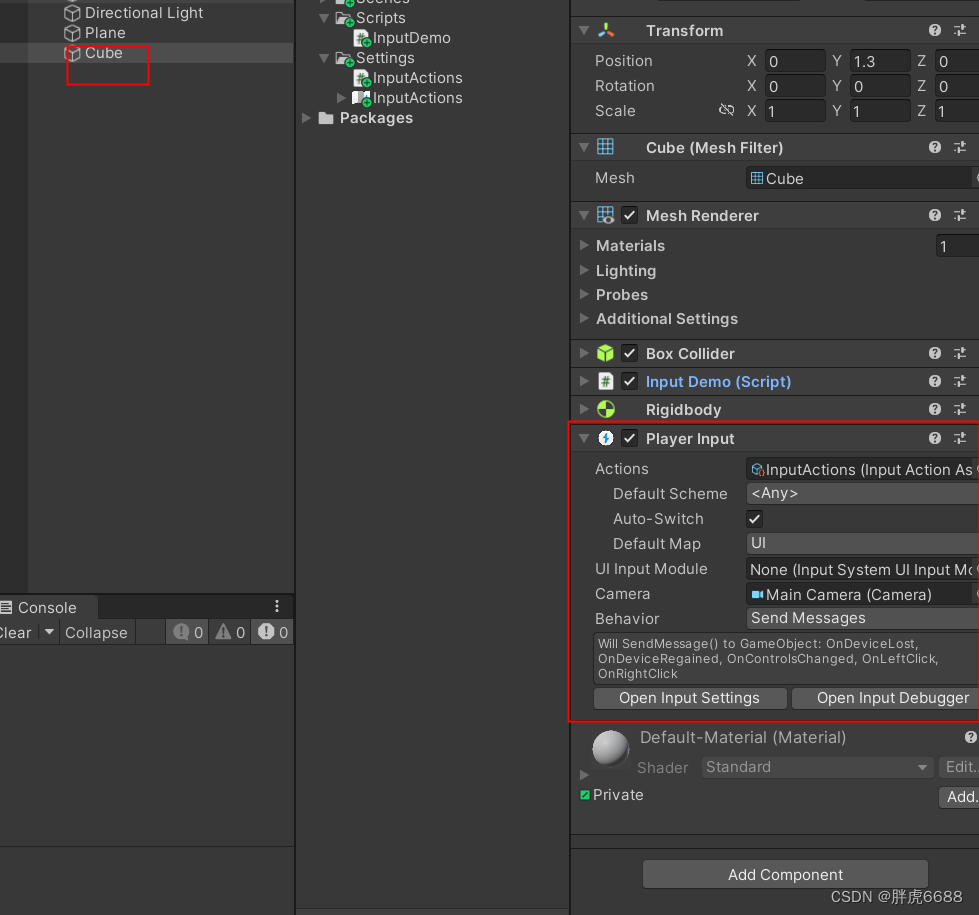
Unity Input System最简单使用
开始学的是 Input Manager 比较好理解,Input System却不好理解,教程也找了很多,感觉都讲的不清楚,我这里做一个最简单的用 Input System 添加鼠标左键和右键的效果。 1. 安装 Input System 包 首先这个功能不是内置的࿰…...
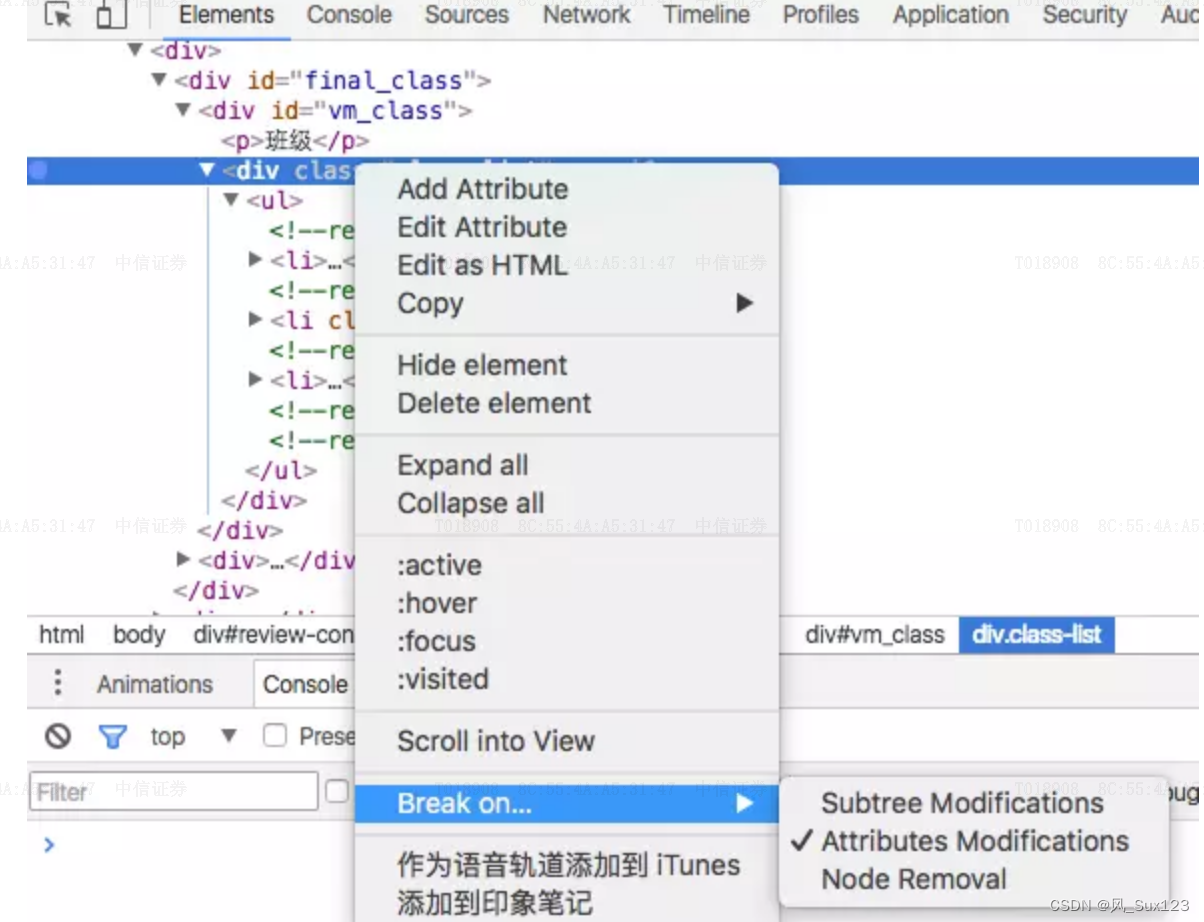
3.前端调式(断点调式)
1. Elements 先来看这张图最上头的一行是一个功能菜单,每一个菜单都有它相应的功能和使用方法,依次从左往右来看 箭头按钮 用于在页面选择一个元素来审查和查看它的相关信息,当我们在Elements这个按钮页面下点击某个Dom元素时,箭…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...